遠程空空導彈中制導策略的分析和評估

王煬，唐碩

(西北工業大學航天學院，陜西西安 710072)

引言

現有文獻中關于遠程空空導彈中制導策略的分析和評估工作主要存在3個問題:(1)中制導策略難以在縱向和側向平面內同時具有較好的飛行性能［1-5］;(2)目標在導彈中制導階段的逃逸效果不佳，使評估結果的可信性受到很大影響［3］;(3)只比較中制導段的飛行時間、末端速度或交班精度，不能全面地反映制導性能的優劣［4］。

本文首先在側向平面內選擇顯式制導方案，在縱向平面內利用奇異攝動理論對導彈動力學模型進行簡化，再利用最優控制理論分別優化設計了兩個平面內的制導方案，可以使遠程空空導彈的中制導段在縱向和側向平面內都具有較好的飛行性能。然后，通過分析目標速度偏角與導彈攻擊脫靶量的關系，得到目標飛行的最大脫靶量方向，也即目標的最有效逃逸方向，改善目標在導彈中制導階段的逃逸效果，提高評估結果的可信性。最后，對靜止目標計算中制導策略對應的射程范圍以及范圍內目標點對應的中制導段的飛行時間和末端能量，分析中制導策略的飛行性能，對機動目標求解導彈的最大攻擊區，評價中制導策略的攻擊能力，從而比較全面地反映中制導策略的綜合性能。

1 中制導策略的評估模型

1.1 遠程空空導彈和目標的模型

用于評估中制導策略的是某型以火箭發動機為動力的遠程空空導彈，初始高度10 km，初始速度Ma=0.8，最大射程100 km，最大飛行高度25 km，最大飛行速度1 000 m/s，最大法向過載40。

遠程空戰主要打擊敵方預警機、電子干擾機、轟炸機等高價值目標，目標飛行空域較廣，飛行速度不高，機動性能不強。不失一般性地選擇目標的飛行高度為5～20 km，飛行速度Ma=0.8，最大法向過載3。導彈和目標機在水平面內的位置關系可以通過水平相對距離R、目標相對導彈的方位角λm以及導彈相對目標的方位角λt來描述，相關定義可以參考文獻［6］。

1.2 遠程空空導彈的混合中制導策略

1.2.1 側向平面的制導策略

根據顯示制導律，可以確定導彈在水平面內一種可行的加速度變化過程為:

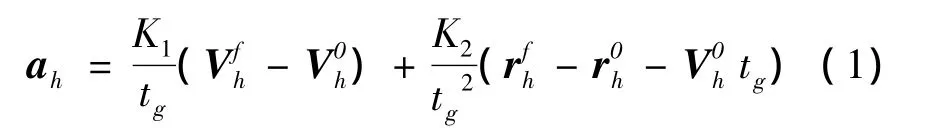
式中，ah，Vh和rh分別為水平面內的導彈加速度、速度和位置矢量;K1和K2為制導系數;tg為剩余飛行時間;角標0和f分別為初始時刻和終端時刻的狀態。

然后選擇水平方向末端速度的最大值為性能指標，取控制量為水平飛行軌跡的曲率κ，它和加速度矢量ah的近似關系為:

式中，φ為速度偏角;δ為水平速度矢量相對于水平目標視線的前置角。最后，利用最優控制理論，得到

式(1)中的制導系數為:

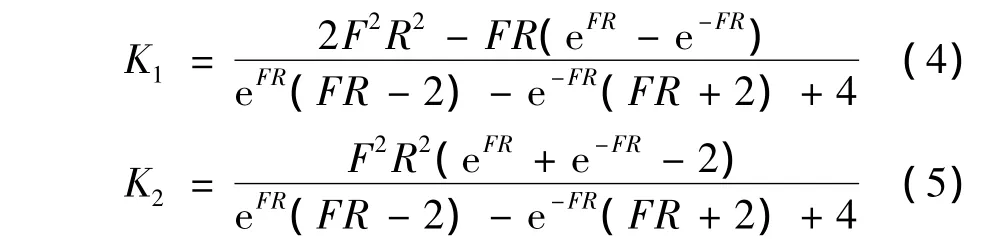
式中，F為與導彈氣動力、推力和狀態量相關的制導參數［5］。

1.2.2 縱向平面的制導策略

利用奇異攝動理論，可以把導彈的運動狀態按4個時間尺度進行分類，如表1所示。

表1 狀態變量的時間常數和時間尺度分類

表中，X，Y，E，H，φ 和 γ 分別表示導彈的縱向位置、側向位置、比能、高度、速度偏角和速度傾角;L和D分別表示升力和阻力;m表示質量;g表示重力加速度常量;Rmax，Vmax，Hmax和Lmax都是與任務相關的特征參數，分別表示導彈的最大射程、最大飛行速度、最大飛行高度以及最大升力。

在最慢的時間尺度上忽略快變量H，φ和γ的動態過程，將H作為控制量，利用最優控制理論得到最優的飛行高度H1滿足:

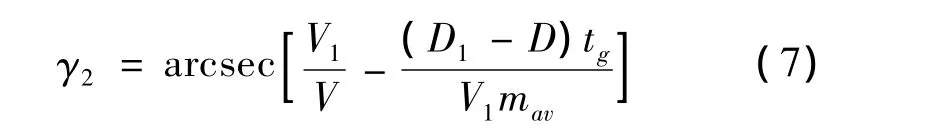
最后，在快變時間尺度上以L作為控制量，利用最優控制理論得到平衡重力以外的升力部分為:

式中，D1為升力與重力相等時對應的阻力大小;V1為H1對應的導彈速度;mav為導彈的平均質量。

然后，在慢變時間尺度上忽略快變量φ和γ的動態過程，把γ作為控制量，利用最優控制理論得到最優的速度傾角γ2為:

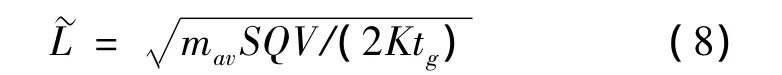
式中，S為氣動參考面積;Q為動壓;K為氣動特性參數［3］。

1.3 導彈和目標的作戰仿真系統

遠程空空導彈和目標的作戰仿真主要有兩個方面的工作:第一是尋找滿足中制導段交班約束條件的可行初始攻擊條件，包括各種彈目初始相對位置和相對速度關系;第二是記錄這些可行初始條件下的中制導段末端飛行參數，包括飛行時間和比能。仿真流程如圖1所示。

在仿真過程中，取導彈中制導段的交班條件為:彈目相對距離R＜5 km，彈目相對速度Vr＞100 m/s，導彈速度矢量相對目標視線的前置角δ＜2°。

取仿真終止條件為以下3種情況之一:

(1)彈上電源關閉之前，始終滿足R＞5 km;

(2)R=5 km之前，存在Vr＜100 m/s的狀態;

(3)R=5 km時，Vr≥100 m/s之前始終滿足δ＞2°。

分析和評估工作中把混合中制導策略(Hybrid)與彈道形成法(TS)和過重力補償比例導引法(CPN)進行比較。另外，由于遠程空空導彈主要考慮前向攻擊的情況，并且評估結果在水平方向上具有一定的對稱性，所以下文的分析過程中，針對彈目初始相對位置關系只給出了λm在0°～90°，以及λt在0°～180°范圍內的分析結果。

2 中制導策略的性能分析

由于實際的評估工作不能夠取所有初始條件下的仿真結果進行分析，因此需要建立一種可行的分析方法，使得所利用的仿真數據盡可能少，所反映的制導策略性能盡可能全面，同時可以得出一些規律性的結論。

2.1 飛行性能的分析

2.1.1 射程范圍

設導彈初始位置在坐標原點上空，初始速度沿x軸正方向，對水平距離20～150 km、高度5～20 km范圍內的靜止目標點進行搜索，分析滿足中制導交班約束條件的導彈射程范圍。圖2～圖4為不同情況的射程范圍。

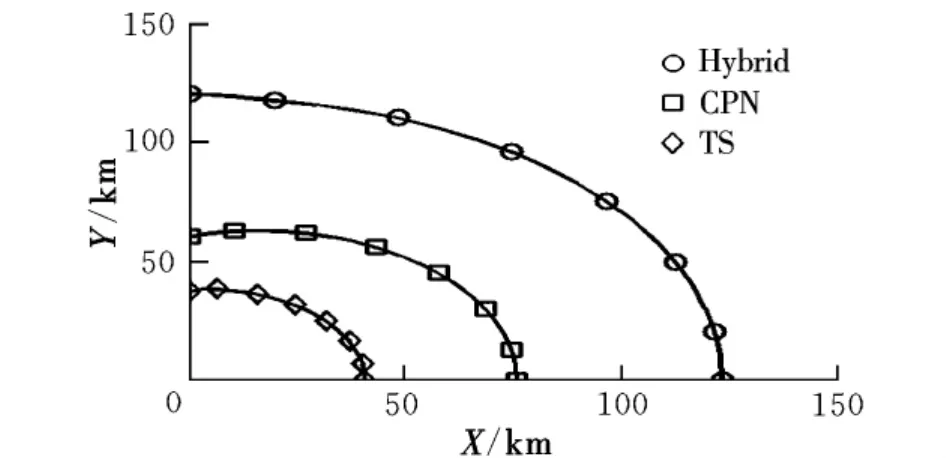
圖2 H=10 km時水平面內的射程范圍

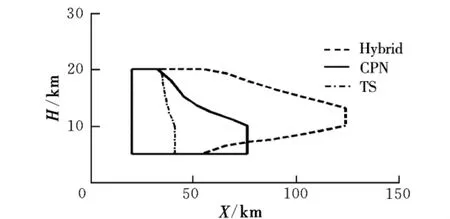
圖3 λm=0°時鉛垂面內的射程范圍

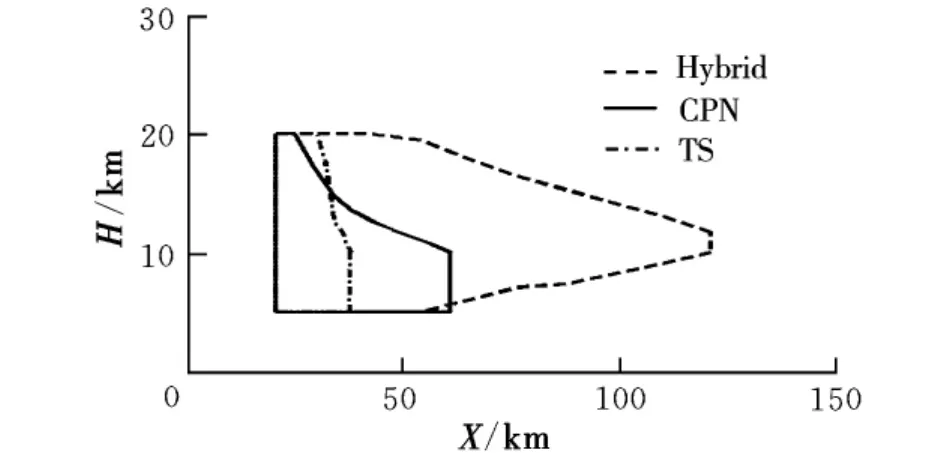
圖4 λm=90°時鉛垂面內的射程范圍

圖2～圖4綜合起來可以表達三維空間內中制導方法對應的導彈射程范圍，從中可以得出以下兩點規律性的結論:(1)給定λm，可到達的高度范圍隨水平相對距離的增大而減小，當彈目初始高度相同時，導彈具有最大的水平射程;(2)由于側向機動的消耗，隨著λm從0°～90°變化，最大水平射程和導彈可到達的高度范圍都在減小。

通過對3種中制導方法對應射程范圍的比較，可以發現以下兩點區別:(1)除了導彈初始位置前下方的某一小部分區域以外，Hybrid策略具有更大的水平射程范圍和可到達的高度范圍;(2)隨著λm從0°～90°增加，Hybrid方法最大水平射程損失不到3%，遠小于TS方法的9%和CPN方法的20%，并且Hybrid策略可到達的高度范圍損失也最小，說明Hybrid策略具有更好的側向機動能力。

因為在彈目具有相同初始高度的情況下，各種中制導方法都具有最大的水平射程，以下針對這種具有優勢的攻擊情況進行具體的分析研究。

2.1.2 中制導段的末端參數

在TS方法對應的10 km高度水平射程范圍內，計算每個目標點對應的中制導段末端能量和飛行時間，對不同方法進行比較。圖5給出了Hybrid和TS兩種方法中制導末端比能的差值分布，等值線上數值的單位為J。圖6給出了Hybrid與CPN兩種方法中制導段飛行時間的差值分布，等值線上數值的單位為s。

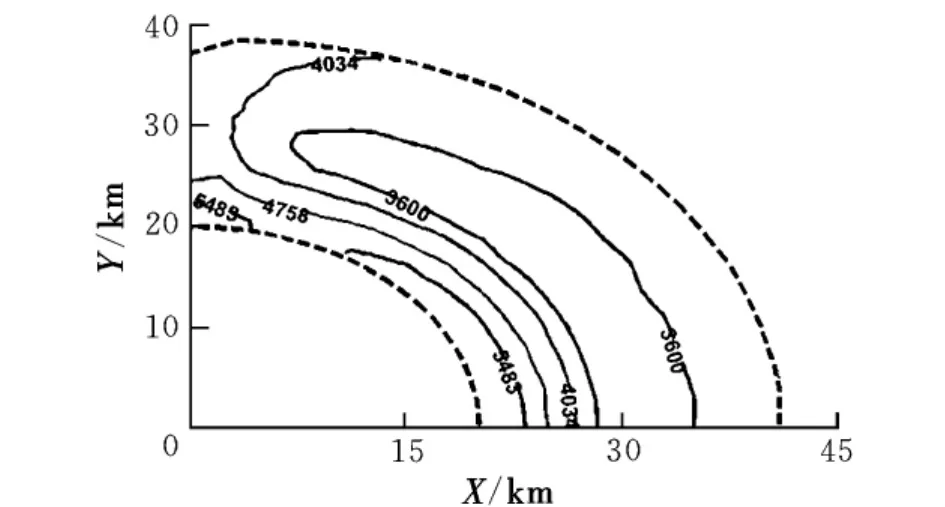
圖5 中制導末端Hybrid與TS方法的比能差值

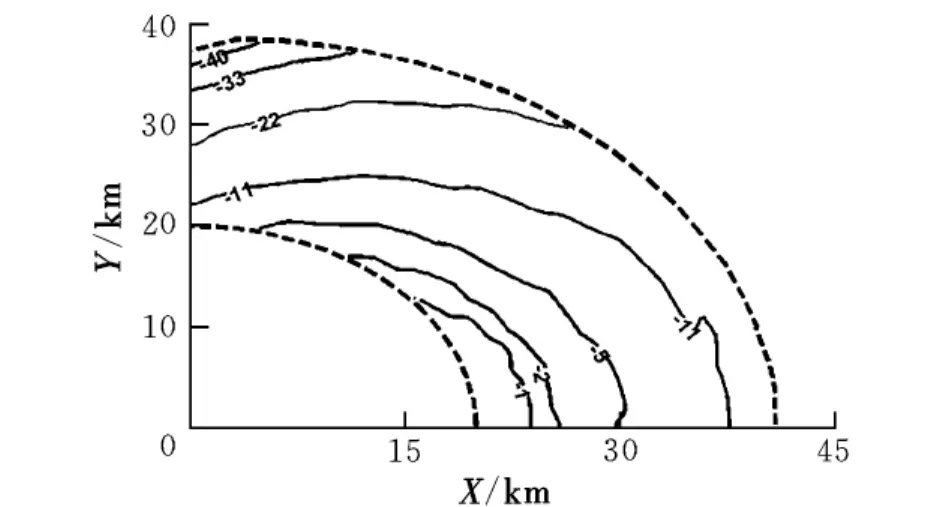
圖6 Hybrid與CPN方法的中制導段飛行時間差值

從中可以得出以下兩點結論:

(1)對相同的目標點，Hybrid策略具有更大的末端能量，這使得遠程空空導彈在末制導段具有更大的機動能力。

(2)對相同的目標點，Hybrid策略具有更短的飛行時間，并且隨著目標距離的增加以及方位角的增大，這種時間優勢變得更明顯，這使得載機在中制導結束時相對目標機的距離更遠，安全性更高，并且再次證明Hybrid策略具有更好的側向機動能力。

類似地，從Hybrid和CPN兩種方法中制導末端比能的差值分布以及Hybrid和TS兩種方法中制導段飛行時間的差值分布中可以得出相同的結論，此處不再詳細列舉。

2.2 作戰性能的分析

設目標的初始高度為10 km，在水平面內飛行，計算以導彈為中心和以目標為中心的導彈最大攻擊區;前者可以表示針對所有目標運動方向的導彈攻擊范圍，特別地，可以反映出導彈的橫向機動能力;后者表示了導彈初始速度指向目標時的攻擊范圍，這種情況在遠程空戰中比較普遍。

2.2.1 目標逃逸策略的分析

設導彈位于坐標原點上空，初始速度沿x軸正方向，針對目標所有的速度偏角ΨT，選取不同的初始彈目方位角λm和初始彈目水平距離R計算導彈攻擊的脫靶量ΔR，導彈末制導律采用增廣比例導引法。

圖7描述了初始彈目方位角λm=30°時Hybrid中制導策略對應的仿真結果，其中每條曲線上標示的數字表示初始彈目水平距離R的大小，其他初始λm情況下得到的曲線具有類似的特征，此處不再詳細列舉。從中可以發現:在指定的初始方位角和相對距離的條件下，目標速度指向導彈初始位置時，導彈攻擊的脫靶量最小，反之脫靶量最大。其他兩種中制導方法可以得到相同的結論。

圖7 Hybrid方法導彈攻擊的脫靶量

由于目標最有效的逃逸方式是時刻沿著導彈脫靶量最大的方向運動，所以在導彈中制導階段，目標應該盡快使導彈相對自身形成并保持尾追，即逃逸制導策略為:

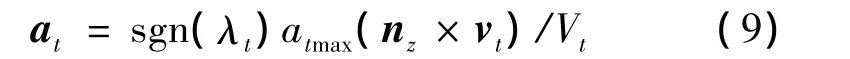
式中，at為目標的逃逸加速度矢量;atmax為目標的最大法向加速度;nz為高度方向的單位矢量。

2.2.2 以導彈為中心的最大攻擊區

設導彈位于坐標原點上空，初始速度沿x軸正方向。通過目標的逃逸策略可知，以導彈為中心的最大攻擊區外邊界由速度指向導彈初始位置的目標位置范圍決定，進而，可以得到3種中制導方法對應的分析結果，如圖8所示。

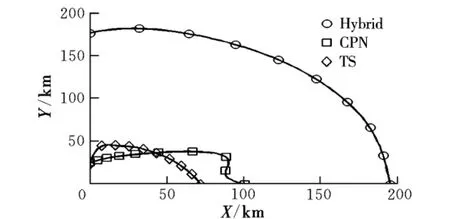
圖8 以導彈為中心的允許發射區外邊界

從圖中可以看出，Hybrid中制導策略具有更大的最大攻擊區，其最大攻擊距離相比其他兩種方法均提高了一倍以上。3種方法的最大攻擊距離隨著目標方位角的增大而減小，其中Hybrid策略的最大攻擊距離損失最小。以上這兩點特征與導彈水平射程范圍的分析結果是類似的。

2.2.3 以目標機為中心的最大攻擊區

當目標進入導彈最大攻擊區后，因為相對距離較遠，載機通常可以先把速度矢量指向目標再發射導彈，以便在中制導段對目標進行跟蹤探測。以目標為中心的導彈最大攻擊區中，導彈的初始速度矢量均指向目標，并假設目標初始位置在坐標原點正上空，初始速度沿x軸正方向。

圖9給出了3種中制導方法對應的分析結果。從中可以看出，遠程空空導彈在迎頭攻擊時具有更大的最大攻擊區，隨著導彈相對目標方位角的減小，攻擊區的范圍也在縮小。這個攻擊區的范圍比以導彈為中心的攻擊區范圍更小、更有針對性，載機的火控系統可以根據這個結果更具體地分析在當前速度方向指向目標時，目標是否處于導彈的有效攻擊范圍之內。

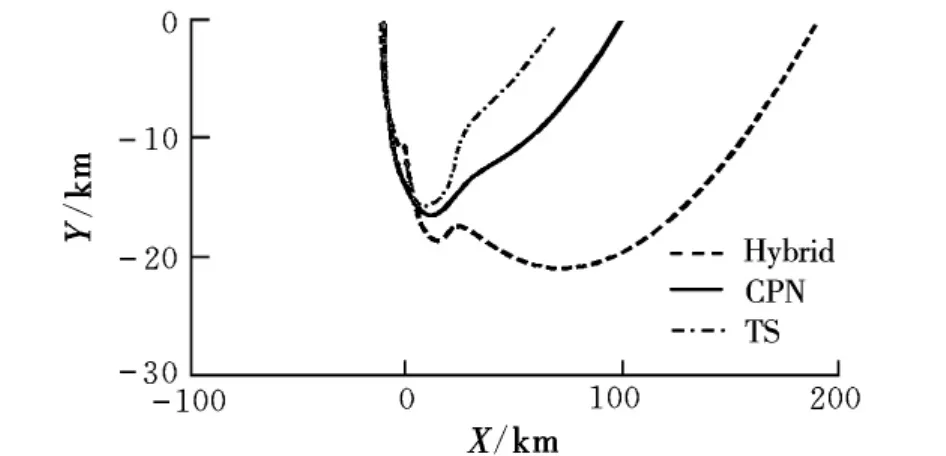
圖9 以目標為中心的發射區外邊界

3 中制導策略的評估結論

結合以上分析，可以得到如下4點分析和評估結論:(1)Hybrid中制導策略比CPN和TS策略具有更大的理論射程范圍和導彈最大攻擊區，并且具有更好的側向機動能力、更大的末端攻擊能量和更短的飛行時間，是一種綜合性能最優的制導策略;(2)遠程空空導彈在與目標處于相同初始高度并且迎頭攻擊時具有更大的最大攻擊區，是一種較好的初始發射條件;(3)中制導階段目標的最佳逃逸策略是盡快使導彈相對自身形成并保持尾追;(4)載機火控系統可以先通過以導彈為中心的最大攻擊區結果分析目標是否處于可攻擊范圍之內，再把速度方向指向目標，通過以目標為中心的導彈最大攻擊區分析是否發射導彈。

4 結論

本文的主要貢獻有以下3點:(1)給出了一種兼顧追蹤精度和軌跡優化能力、在縱向和側向制導平面內都具有較好飛行性能的混合制導策略。相比于其他中制導方法，在最小能量消耗、最小飛行時間、射程范圍和最大攻擊區4個方面都具有明顯的優勢。(2)通過分析，得出了目標在導彈中制導階段最有效的逃逸策略。在此基礎上，求解了導彈的最大攻擊區，提高了分析和評估結果的可信性。(3)提出了一種中制導性能的分析和評估方法，綜合考慮了導彈和目標的各種可能的初始運動條件，以及導彈和目標的制導策略，與其他方法相比，結果和結論更為全面。

［1］ 黃漢橋，周軍，郭建國.具有角度和時間約束的導彈最優全彈道設計［J］.西北工業大學學報，2010，28(2):165-170.

［2］ 富立，范耀祖，寧文如.一種簡單的中遠程空空導彈中制導律研究［J］.航空學報，1998，19(7):92-95.

［3］ Cheng V H L，Gupta N K.Advanced midcourse guidance for air-to-air missiles［J］.Journal of Guidance，1986，9(2):135-142.

［4］ 董朝陽，周雨.一種交班時刻性能最優的中制導律設計與仿真［J］.系統仿真學報，2009，21(24):7873-7882.

［5］ Lin C F，Tsai L L.Analytical solution of optimal trajectory-shaping guidance［J］.Journal of Guidance，1987，10(1):61-66.

［6］ Bonanni P.The art of the kill［M］.Alameda，California:Spectrum HoloByte，1993.