烷基自由基β位裂解反應類反應勢壘與速率常數的精確計算

汪必耀 談寧馨 姚 倩李澤榮,* 李象遠

(1四川大學化學學院,成都610064; 2四川大學化學工程學院,成都610065)

1 引言

燃料在發動機燃燒室的點火成功與否以及燃燒釋放的能量是否達到發動機的需要,會大大影響發動機的工作效率.因此對燃燒的詳細反應機理的研究是一項非常有意義的工作.碳氫燃料是自然界最普遍的燃料,然而碳氫燃料的燃燒是一個復雜的過程,燃燒的詳細反應動力學機理含有大量的基元反應,涉及到數百種物質和成千上萬個反應,1,2復雜的反應機理使得即使較為簡單的燃燒現象也難于模擬.但在這成千上萬個反應中,很多反應屬于相同的一類,3,4而反應類的數目是有限的,這成為很多機理自動生成的出發點.碳氫燃料的燃燒模擬在燃燒機理的研究中起著越來越重要的作用,而可靠的詳細反應機理(包括反應列表、熱力學數據和動力學數據)是其關鍵.碳氫化合物的燃燒和裂解中都涉及到大量的裂解反應,目前僅有少數簡單碳氫化合物自由基裂解反應的動力學實驗數據有文獻報道.5-9烷基自由基β位裂解反應是一類生成小分子烯烴和烷基的重要燃燒反應,在溫度較高的燃燒體系中此類反應有著舉足輕重的作用.10

近年來,Truong等11-17把反應類過渡態理論概念引入到動力學計算中,此方法基于傳統過渡態理論并能結合較低水平從頭算方法精確計算同一類反應的速率常數.反應類過渡態理論的基本思想是同一類反應中所有反應均有相同的反應中心,即沿著反應坐標的勢能面上存在某些相似之處.對于和主反應同類的其他反應的速率常數僅從它們間的勢壘差與主反應的速率常數就可準確計算得到.根據Truong等11-17的研究結果發現,同類反應中的某些熱力學性質是近似不變量,如過渡態的振動虛頻、參考反應與目標反應的勢壘差等.由于參考反應與目標反應的勢壘差隨不同從頭算理論方法的變化不大,反應類過渡態理論即可通過低水平的從頭算理論方法精確計算大分子體系的動力學性質.對于參考反應與目標反應間的勢壘差不隨不同精度從頭算方法變化而變化的原因,Truong等并沒有做進一步闡述.眾所周知構建等鍵反應方法計算的反應焓變隨不同水平從頭算方法的變化不大,18,19因為在等鍵反應中反應物和產物所有鍵的類型和數目都是守恒的,由非完全基組和電子能量修正所導致的誤差在計算反應焓變時得以抵消,20繼而提高計算精度.而本文將把等鍵反應引入到同類反應動力學性質的精確計算中,并稱其為反應類等鍵反應方法.

2 理論方法

在同一類反應中取任意兩反應,其中RP為主反應,RT為目標反應:

反應(1)和(2)對應的過渡態生成反應分別為:

其中ΔVP≠和ΔVT≠分別為反應(3)和反應(4)的反應能,即分別為主反應RP和目標反應RT的反應勢壘.由式(4)減去式(3)得到以下反應:

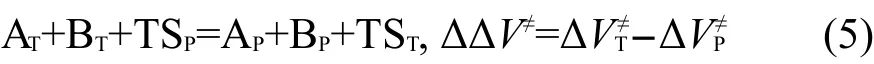
其中ΔΔV≠為該反應的反應能,即目標反應RT和主反應RP的勢壘差.由于反應(5)涉及過渡態,而過渡態的幾何結構常涉及扭曲的化學鍵,所以不能按傳統的等鍵反應方法通過計算反應前后典型鍵的數目來判斷反應是否為等鍵反應.由于反應(5)為同一類型的兩反應對應的過渡態的生成反應相減得到,而同一類型的兩反應有相同的反應中心和不同的取代基團,則反應(5)可以劃分為兩部分:兩反應涉及的取代基團和兩反應的反應中心,可以很容易證明取代基團涉及到的典型鍵的數目在反應(5)的反應前后是相同的.如果兩反應的反應中心的幾何結構相同或非常接近,我們可以把反應(5)視為等鍵反應.在這種情況下,根據等鍵反應原理,ΔΔV≠為等鍵反應的反應能,應隨從頭算理論水平的變化而變化不大,即通過低水平從頭算方法亦能得到較精確的計算結果.設反應勢壘ΔVP≠?、ΔVT≠?為可靠實驗值或高水平從頭算方法的計算結果,而反應勢壘ΔVP≠、ΔVT≠由較低水平從頭算方法計算得到,則它們應近似地滿足以下關系式:

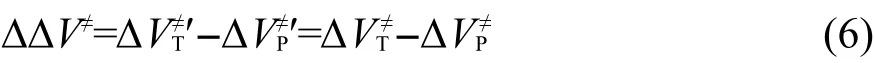
因而有:

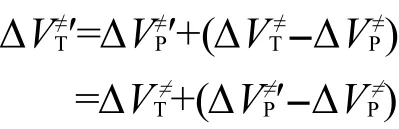
其中:ΔΔVP≠為主反應精確反應勢壘和近似反應勢壘的差值,即主反應的反應勢壘的修正值.式(7)即為利用反應類等鍵反應方法計算目標反應的精確反應勢壘的表達式,表明目標反應的精確反應勢壘可以由其低水平計算的近似結果通過主反應的修正值修正得到.這就解釋了Truong等在反應類過渡態理論里所涉及到同類反應中主反應與目標反應的勢壘差值不隨從頭算水平變化而變化的表述.由于精確計算只涉及到主反應而不涉及目標反應,所以目標反應只涉及到低從頭算水平的近似計算,而主反應又通常選擇較小的分子反應體系.因此根據該修正方法,可以在低從頭算水平下得到目標反應的精確反應勢壘,從而解決了大分子反應體系動力學參數的精確計算問題.

烷基自由基β位裂解反應是碳氫化合物在高溫條件下燃燒所涉及的非常重要的一類反應,10其裂解產物為烯烴和烷基自由基.本文選取了以下13個烷基自由基的β位裂解反應作為研究體系,以檢驗反應類等鍵反應方法的計算精度及普適性:

其中最小的反應體系R1選為主反應.所有反應涉及到的物種的幾何結構優化和頻率計算均在BHandHLYP/cc-pVDZ水平下進行,并用內稟反應坐標(IRC)理論21對體系中反應通道進行了確認.由于主反應R1的反應勢壘沒有相關的實驗數據和文獻報道,因此本文選用高精度CCSD(T)/cc-pVXZ (X=D,T,Q)22-26方法外推到完全基組法計算主反應中各物種的精確單點能:

其中,Hartree-Fock完全基組能量EHF∞由HF/cc-pVXZ (X=D,T,Q)外推得到:

完全基組相關能Ecor∞由CCSD(T)/cc-pVXZ(X=D,T)外推得到:

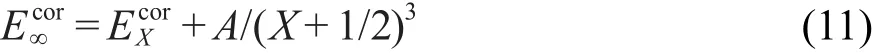
通過式(11)求得的各物種的單點能進一步用于計算主反應的精確反應勢壘?V1≠?.本文選取了5個目標反應R2、R3、R4、R5、R6作為測試集,用不同從頭算近似方法直接計算了這5個目標反應的反應勢壘,進一步用反應類等鍵反應方法進行了修正,并與高精度從頭算方法的結果進行比較.本文共考察了10種近似從頭算方法,標記為L1,L2,…,L10,他們分別是:L1:HF/cc-pVDZ;L2:BHandHLYP/cc-pVDZ;L3: B3LYP/cc-pVDZ;L4:BP86/cc-pVDZ;L5:TPSS/ccpVDZ;L6:B3P86/cc-pVDZ;L7:O3LYP/cc-pVDZ; L8:MP2/aug-cc-pVDZ;L9:CCSD(T)/cc-pVDZ;L10: CCSD(T)/aug-cc-pVDZ.這些方法可劃分為四個級別:Hartree-Fock(L1),DFT(L2-L7),MP2(L8),CCSD所有從頭算計算均在Gaussion 03程序27上完成.

3 結果與討論

3.1 過渡態的反應中心幾何結構

用BHandHLYP/cc-pVDZ方法優化后的過渡態反應中心所涉及到的原子、鍵長與鍵角編號如圖1所示.其中d1、d2為鍵長,A1為鍵角,Ra、Rb、Rc、Rd、Re、 Rf、Rg代表過渡態中烷基或氫取代基.過渡態反應中心的優化幾何結構參數列于表1中.

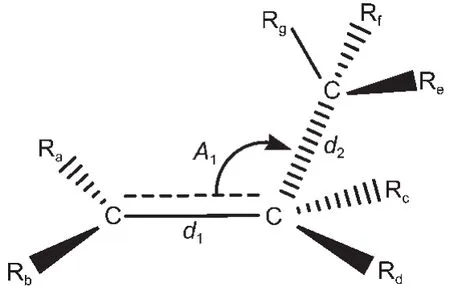
圖1 過渡態反應中心的幾何結構Fig.1 Geometry structures for the reaction center of the transition state

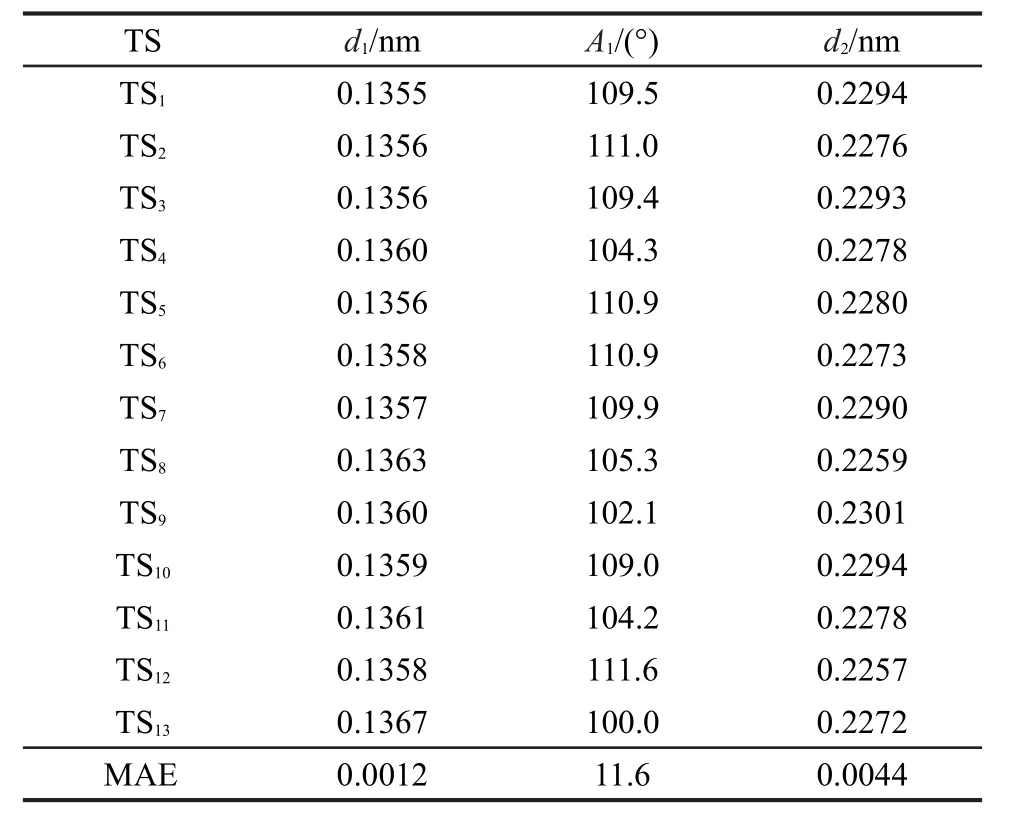
表1 過渡態反應中心優化后的幾何參數Table 1 Optimized geometrical parameters of reaction center of transition state

由表1所列出的數據可以看出,同類反應的過渡態反應活性中心的幾何結構幾乎相同,新形成的雙鍵d1和將斷裂的鍵d2的最大絕對誤差僅為0.0012和0.0044 nm,兩者間夾角的最大誤差也僅為11.6°,所以由任意兩過渡態生成反應所組成的代數差反應中的過渡態反應中心的幾何結構是守恒的,由體系中任意兩過渡態的生成反應的差所構建的反應即為等鍵反應.

3.2 不同從頭算水平計算的主反應的反應勢壘

用選取的10種近似從頭算方法及CCSD(T)/ cc-pVXZ(X=D,T,Q)水平下的完全基組外推法計算了主反應的反應勢壘,結果列于表2.

表2中的結果顯示出不同從頭算方法的計算結果相差較大,以精確的完全基組外推法CCSD(T)/ CBS作為不同計算方法對勢壘結果影響的比較基準,近似從頭算方法勢壘值的最大偏差與最小偏差分別來自TPSS/cc-pVDZ方法的12.57 kJ·mol-1和O3LYP/cc-pVDZ方法的-2.11 kJ·mol-1.由此可以看出在本研究體系中,O3LYP/cc-pVDZ方法的計算精度甚至高于CCSD(T)/aug-cc-pVDZ方法.但由于不同DFT方法對不同體系的計算結果相差較大,因此并不具有普適性.而表中??VP≠項用于后文對低水平從頭算方法下的目標反應的反應勢壘進行校正.

3.3 反應勢壘的直接計算與等鍵反應修正的結果比較

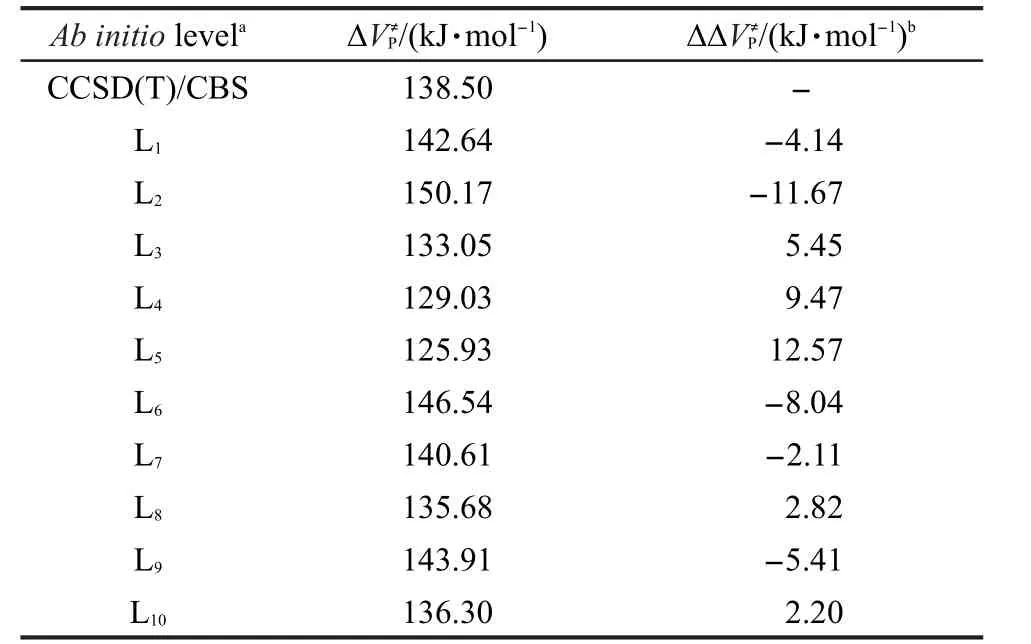
表2 主反應R1在各水平從頭算方法下的反應勢壘Table 2 Reaction barriers at various ab initio levels for the principal reaction R1

本文從烷基自由基β位裂解反應的體系中選取5個代表反應R2、R3、R4、R5、R6,分別在Hartree-Fock (L1),DFT(L2-L7),MP2(L8),CCSD(T)(L9-L10)水平下對這些反應的反應勢壘進行了計算,并用反應類等鍵反應方法進行了修正,結果列于表3.

由于本文所選擇的研究體系缺乏對應的實驗勢壘數據,因此文中選擇以較精確的CCSD(T)/ aug-cc-pVDZ方法(表3中L10)作為不同從頭算方法比較反應勢壘計算精度的基準.從表3中的數據可以看出,不同從頭算方法對同一反應的直接計算結果相差較大,其中最大絕對偏差(MAE)可達17.43 kJ·mol-1,5個代表反應的最大絕對偏差的平均值亦有16.16 kJ·mol-1.而利用反應類等鍵反應方法校正后的最大絕對偏差為7.64 kJ·mol-1,5個代表反應的最大絕對偏差的平均值也僅有5.32 kJ·mol-1.表明在本體系中用反應類等鍵反應方法計算的反應勢壘對從頭算方法的級別和基組的大小依賴性小,反應類等鍵反應方法在較低從頭算水平即可再現較高從頭算水平結果.

3.4 目標反應的反應勢壘

對于烷基自由基β位裂解反應類中所有目標反應的反應勢壘,我們均采用低水平的BHandHLYP/ cc-pVDZ方法并通過反應類等鍵反應方法校正獲得,相應結果列于表4.

3.5 反應速率常數的計算

根據傳統過渡態理論,反應:

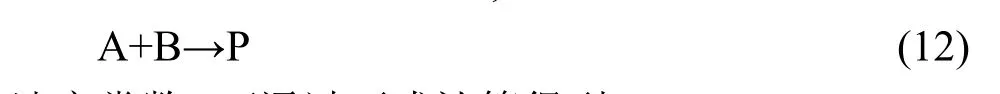
速率常數k可通過下式計算得到:

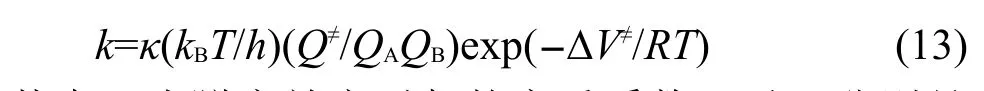
其中:κ為隧穿效應引起的穿透系數,kB和h分別是Boltzmann常數和Planck常數,T為熱力學溫度,R為摩爾氣體常數,Q≠、QA、QB分別是過渡態、反應物A、反應物B的配分函數,?V≠為過渡態電子能量與反應物電子能量之差,即反應的能壘.以上配分函數不包含電子運動的貢獻,只包含振動、轉動和平動的貢獻,僅與優化得到的幾何結構和振動頻率有關,而與單點能計算無關,因此單點能計算的從頭算級別只影響反應的能壘.根據前面引入的反應類過渡態理論,設在某一從頭算水平直接計算得到的反應能壘和由反應類過渡態理論修正后的反應能壘分別為?V≠及?V≠',計算得到的反應速率常數分別為k及k',則有:

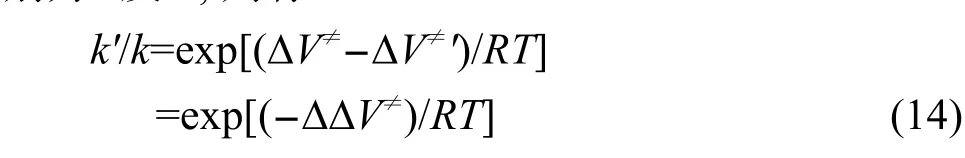
即:

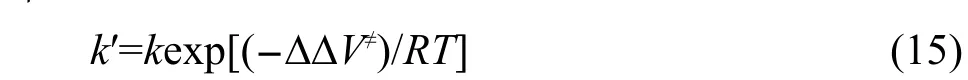
其中:??V≠即為式(7)、(8)定義的能壘修正值.根據式(15),由低水平從頭算方法得到的速率常數通過反應類等鍵反應方法校正可以獲得類反應的精確速率常數.

本文中類反應體系的每一個反應的速率常數均通過基于傳統過渡態理論框架下的TheRate軟件28計算獲得,并應用Eckart方法29對隧穿效應進行校正.

與3.4節一樣,主反應分別在CCSD(T)/CBS和BHandHLYP/cc-pVDZ水平計算得到能壘修正值為-11.67 kJ·mol-1(見表2).體系中所有目標反應單點能均為BHandHLYP/cc-pVDZ水平.燃燒動力學模擬需要的動力學參數通常是根據改進Arrhenius方程:

其中:A為指前因子,E為阿侖尼烏斯活化能,n為常數.對過渡態理論計算得到的不同溫度下速率常數k(T)擬合,以參數(A,n,E)形式給出.

本文為了驗證反應類等鍵反應方法對類反應速率常數的計算精度,對文獻7,30-39中有實驗速率常數報道的反應R2、R3、R4,用反應類等鍵反應方法計算了在溫度范圍為500-2000 K的速率常數,并與文獻報道實驗值7,30-39進行了比較,比較結果列于表5.為了方便比較,我們定義速率常數比值kmax/kmin為計算值與實驗值中較大速率常數與較小速率常數的比值,并將3個代表反應的kmax/kmin在溫度范圍為500-2000 K下的最大值MD與平均值AD分別列于表5.

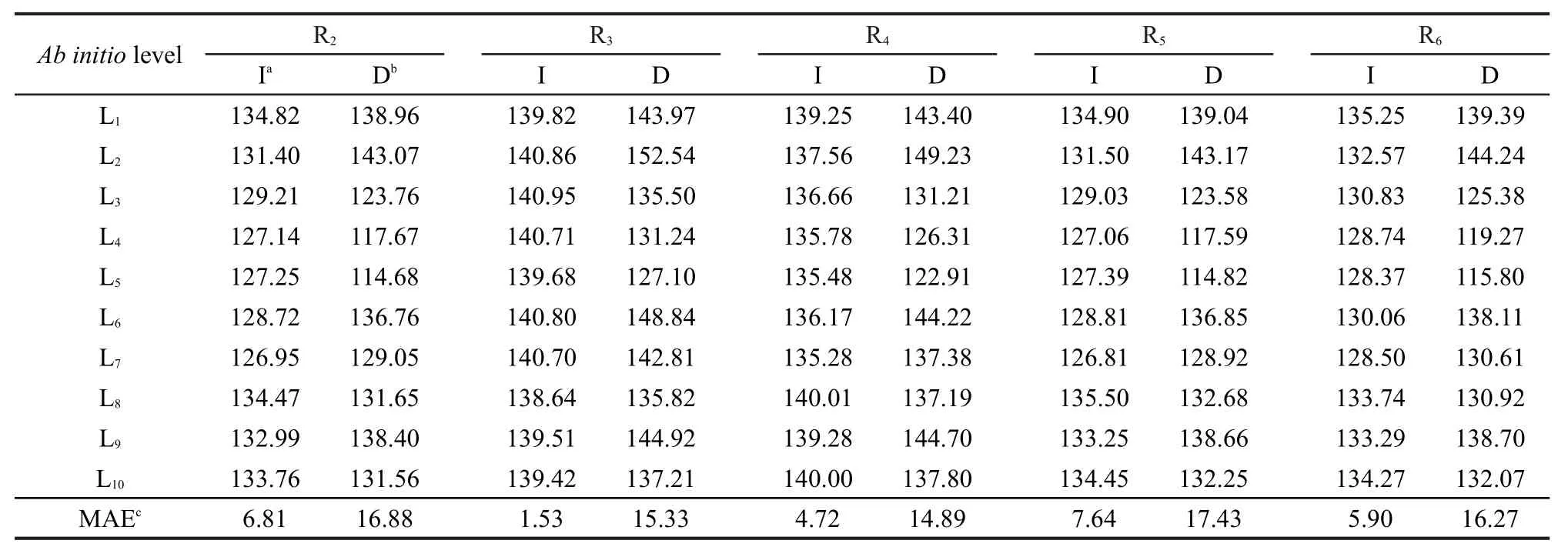
表3 代表反應的反應勢壘(單位:kJ·mol-1)Table 3 Reaction barriers of the representative reactions(unit in kJ·mol-1)

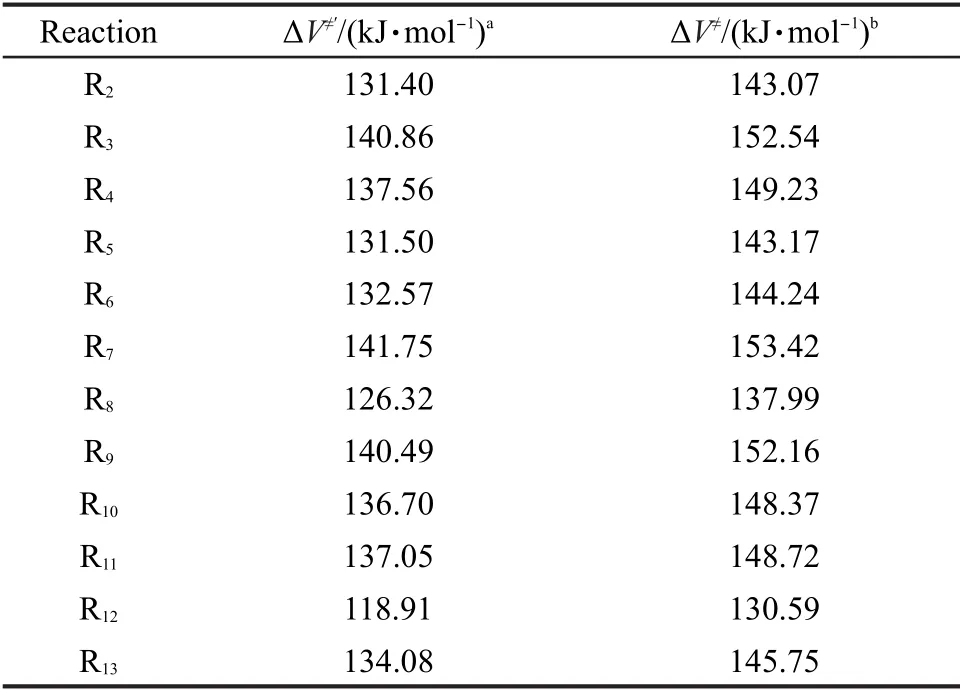
表4 由反應類等鍵反應方法計算的反應勢壘Table 4 Reaction barriers calculated by reaction class isodesmic reaction method

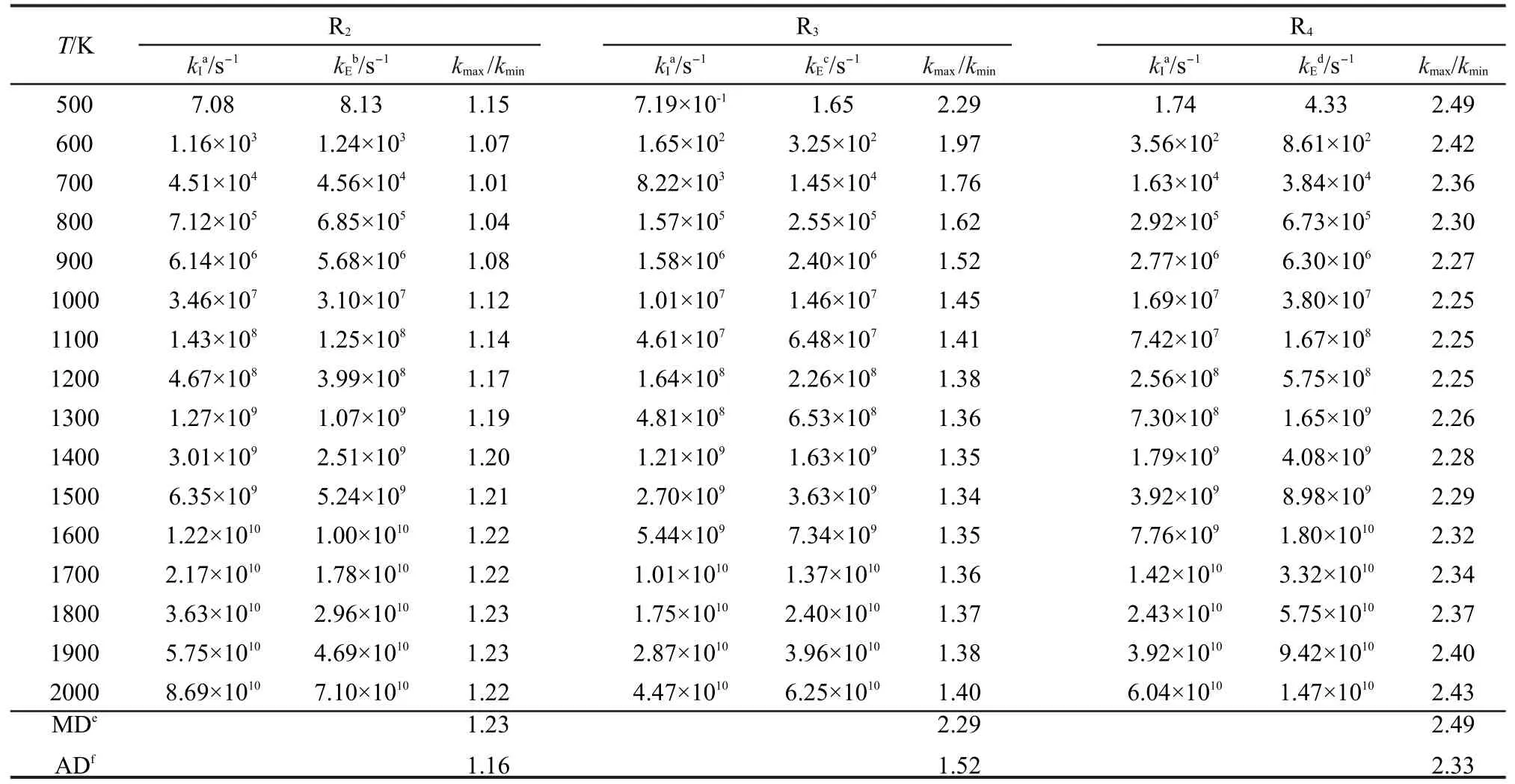
表5 過渡態理論速率常數的反應類過渡態理論方法計算值與實驗值的比較Table 5 Comparison of transition state theory rate constants from the reaction class isodesmic reaction method calculations and the experiment values

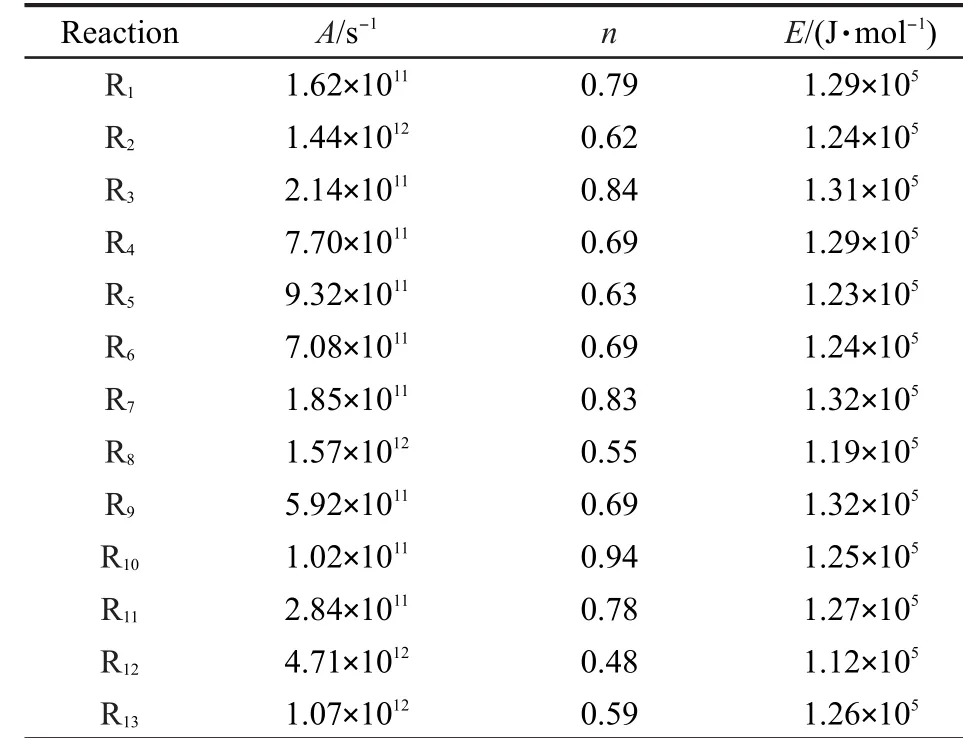
表6 動力學參數(A,n,E)的計算Table 6 Calculated kinetic parameters(A,n,E)

從表5中的數據看出,通過反應類等鍵反應方法校正后的3個代表反應在溫度范圍為500-2000 K的速率常數與文獻報道的實驗值非常接近.3個代表反應在500-2000 K溫度內kmax/kmin的平均值僅為1.67,單個反應kmax/kmin的最大平均值也僅為2.33,最大值也只有2.49.因此應用反應類等鍵反應方法精確校正同類反應低精度下的速率常數是高效而可行的,同時此方法亦能在低計算要求和低耗時情況下獲得較高的計算精度,從而為大分子反應的高精度速率常數計算創造了有利條件.

表6給出了由反應類等鍵反應方法校正得到的速率常數擬合得到的各反應動力學參數(A,n,E).

4 結論

提出了在低從頭算水平下精確計算類反應能壘及速率常數的反應類等鍵反應方法,并用于烷基自由基β位裂解反應體系.通過在不同從頭算水平和不同基組下對其中5個代表反應體系的反應能壘的對比計算發現,用反應類等鍵反應方法計算的反應勢壘對從頭算方法的級別和基組的大小依賴性小,利用反應類等鍵反應方法,可將直接從頭算方法獲得的反應勢壘平均最大絕對偏差16.16 kJ· mol-1降低到5.32 kJ·mol-1.用反應類等鍵反應方法計算了烷基自由基β位裂解反應體系的反應能壘、不同溫度下的速率常數,并擬合得到(A,n,E)形式的各反應動力學參數.對其中有文獻實驗速率常數報道的3個反應,其計算速率常數和實驗速率常數比值kmax/kmin在500-2000 K溫度段內的平均值僅為1.67,單個反應的最大比值為2.49,表明反應類等鍵反應方法可計算得到與實驗相近的速率常數.因此本文工作表明,反應類等鍵反應方法可在低從頭算水平計算得到類反應體系精確的反應勢壘和速率常數,可解決大分子體系動力學參數的精確計算問題.

(1) Lu,T.F.;Law,C.K.Combust.Flame 2006,144,24.doi: 10.1016/j.combustflame.2005.02.015

(2) Pepiot-Desjardins,P.;Pitsch,H.Combust.Flame 2008,154,67. doi:10.1016/j.combustflame.2007.10.020

(3) Curran,H.J.;Gaffuri,P.;Pitz,W.J.Combust.Flame 1998,114, 149.doi:10.1016/S0010-2180(97)00282-4

(4) Curran,H.J.;Gaffuri,P.;Pitz,W.J.Combust.Flame 2002,129, 253.doi:10.1016/S0010-2180(01)00373-X

(5) Knyazev,V.D.;Bencsura,A.;Dubinsky,I.A.;Gutman,D.; Senkan,S.M.Proc.Combust.Inst.1994,25,817.

(6) Knyazev,V.D.;Dubinsky,I.A.;Slagle,I.R.;Gutman,D. J.Phys.Chem.1994,98,5279.doi:10.1021/j100071a018

(7) Knyazev,V.D.;Dubinsky,I.A.;Slagle,I.R.;Gutman,D. J.Phys.Chem.1994,98,11099.doi:10.1021/j100094a018

(8) Slagle,I.R.;Batt,L.;Gmurczyk,G.W.;Gutman,D.;Tsang,W. J.Phys.Chem.1991,95,7732.doi:10.1021/j100173a034

(9) Bencsura,A.;Knyazev,V.D.;Xing,S.B.;Slagle,I.R.; Gutman,D.Proc.Combust.Inst.1992,24,629.

(10) Zheng,X.B.;Blowers,P.Ind.Eng.Chem.Res.2006,45,530. doi:10.1021/ie0508942

(11)Truong,T.N.J.Chem.Phys.2000,113,4959.

(12) Huynh,L.K.;Ratkiewicz,A.;Truong,T.N.J.Phys.Chem.A 2006,110,473.doi:10.1021/jp051280d

(13)Muszynska,M.;Ratkiewicz,A.;Huynh,L.K.;Truong,T.N. J.Phys.Chem.A 2009,113,8327.doi:10.1021/jp903762x

(14) Bankiewicz,B.;Huynh,L.K.;Ratkiewicz,A.;Truong,T.N.J. Phys.Chem.A 2009,113,1564.doi:10.1021/jp808874j

(15) Zhang,S.W.;Truong,T.N.J.Phys.Chem.A 2003,107,1138. doi:10.1021/jp021265y

(16) Kungwan,N.;Truong,T.N.J.Phys.Chem.A 2005,109,7742. doi:10.1021/jp051799+

(17) Huynh,L.K.;Truong,T.N.Theor.Chem.Acc.2008,120,107. doi:10.1007/s00214-007-0311-9

(18) Hehre,W.J.;Ditchfield,R.;Radom,L.;Pople,J.A.J.Am. Chem.Soc.1970,92,4796.doi:10.1021/ja00719a006

(19) Radom,L.;Hehre,W.J.;Pople,J.A.J.Am.Chem.Soc.1971, 93,289.doi:10.1021/ja00731a001

(20)Wiberg,K.B.;Ochterski,J.W.J.Comput.Chem.1997,18,108.

(21) Gonzalez,C.;Schlegel,H.B.J.Phys.Chem.1990,94,5523. doi:10.1021/j100377a021

(22) Truhlar,D.G.Chem.Phys.Lett.1998,294,45.doi:10.1016/ S0009-2614(98)00866-5

(23) Halkier,A.;Helgaker,T.;Jorgensen,P.J.Chem.Phys.Lett. 1999,302,437.doi:10.1016/S0009-2614(99)00179-7

(24)De Lara-Castells,M.P.;Krems,R.V.;Buchachenko,A.A.J. Chem.Phys.2001,115,10438.doi:10.1063/1.1415078

(25) Huh,S.B.;Lee,J.S.J.Chem.Phys.2003,118,3035.doi: 10.1063/1.1534091

(26) Hwang,R.;Park,Y.C.;Lee,J.S.Theor.Chem.Acc.2006,115, 54.doi:10.1007/s00214-005-0675-7

(27) Frisch,M.J.;Trucks,G.W.;Schlegel,H.B.;et al.Gaussian 03, Revision B.01;Gaussian Inc.:Pittsburgh,PA,2003.

(28)Duncan,W.T.;Bell,R.L.;Truong,T.N.J.Comput.Chem. 1998,19,1039.

(29) Eckart,C.Phys.Rev.1930,35,1303.doi:10.1103/ PhysRev.35.1303

(30)Morganroth,W.E.;Calvert,J.G.J.Am.Chem.Soc.1966,88, 5387.doi:10.1021/ja00975a004

(31) Knyazev,V.D.;Slagle,I.R.J.Phys.Chem.1996,100,5318. doi:10.1021/jp952229k

(32) Kerr,J.A.;Trotman-Dickenson,A.F.J.Chem.Soc.1960,323, 1602.

(33) Gierczak,T.;Gawlowski,J.;Niedzielski,J.React.Kinet.Catal. Lett.1988,36,434.

(34)Tsang,W.J.Am.Chem.Soc.1985,107,2872.doi:10.1021/ ja00296a007

(35) Lin,M.C.;Laidler,K.J.Can.J.Chem.1967,45,1315.

(36) Gang,J.;Pilling,M.J.;Robertson,S.H.J.Chem.Soc.Faraday Trans.1997,93,1481.doi:10.1039/a607566e

(37) Metcalfe,E.L.;Trotman-Dickenson,A.F.J.Chem.Soc.1960, 980,5072.

(38) Slater,D.H.;Collier,S.S.;Calvert,J.G.J.Am.Chem.Soc. 1968,90,268.doi:10.1021/ja01004a010

(39) Douhou,S.;Perrin,D.;Martin,R.J.Chim.Phys.1994,91, 1628.