排隊(duì)論G/Ek/c模型及其在醫(yī)院眼科專家門診中的應(yīng)用
章順悅 楊 揚(yáng) 吳家利 宋婷婷 陳遠(yuǎn)方 劉文華 尹 平△
近年來(lái),排隊(duì)論模型在醫(yī)療服務(wù)領(lǐng)域中的應(yīng)用受到了極大地關(guān)注〔1-2〕。由于醫(yī)療資源的相對(duì)短缺,一些大型綜合性醫(yī)院的排隊(duì)擁擠現(xiàn)象普遍存在。但病人到達(dá)醫(yī)療機(jī)構(gòu)的間隔時(shí)間分布往往又不可控,例如交通狀況,天氣、季節(jié)因素,病人流量和坐診醫(yī)生的口碑,以及目前興起的預(yù)約排隊(duì)與窗口排隊(duì)結(jié)合等都可能影響病人的到達(dá),難以用確切的概率分布函數(shù)來(lái)表達(dá)。而排隊(duì)論G/Ek/c模型則可較好的解決此類復(fù)雜問(wèn)題。本文通過(guò)介紹排隊(duì)論G/Ek/c模型的原理與參數(shù)估計(jì),并對(duì)武漢市某大型綜合性醫(yī)院的眼科專家門診就診患者的排隊(duì)數(shù)據(jù)進(jìn)行擬合,以期為優(yōu)化醫(yī)院眼科專家門診的人力資源配置,縮短病人的排隊(duì)等候時(shí)間提供科學(xué)的決策依據(jù)。
G/Ek/c模型的基本結(jié)構(gòu)
G/Ek/c模型指顧客的到達(dá)規(guī)律服從一般分布(G),服務(wù)時(shí)間服從愛(ài)爾朗分布(Ek),有c個(gè)服務(wù)臺(tái)的排隊(duì)論模型。其對(duì)顧客的到達(dá)時(shí)間分布沒(méi)有特定限制,適用范圍廣泛。以醫(yī)院眼科專家門診為例,介紹該模型的結(jié)構(gòu)。
1.顧客源
顧客源是指接受服務(wù)的對(duì)象。醫(yī)院眼科專家門診就診的病人即為顧客源,假設(shè)其為無(wú)限。病人到門診的分布受到很多因素影響,其間隔時(shí)間可認(rèn)為服從一般分布(G)。
2.隊(duì)列
在得到服務(wù)前等待的病人組成隊(duì)列,以其能容納的最大顧客數(shù)量為標(biāo)志。醫(yī)院的隊(duì)列多由若干個(gè)隊(duì)長(zhǎng)組成(如3名專家坐診,則由3個(gè)隊(duì)長(zhǎng)組成隊(duì)列),而且患者掛號(hào)后通常不會(huì)因?yàn)榕抨?duì)的隊(duì)伍太長(zhǎng)而輕易離開(kāi),視為無(wú)限隊(duì)長(zhǎng)。
3.排隊(duì)規(guī)則
排隊(duì)規(guī)則指服務(wù)機(jī)構(gòu)是否允許顧客排隊(duì),顧客對(duì)排隊(duì)長(zhǎng)度、時(shí)間的容忍程度以及在排隊(duì)隊(duì)列中等待服務(wù)的順序。該專家門診按照先到先服務(wù)(FCFS)的等待制排隊(duì)規(guī)則,但中間插入了之前預(yù)約的患者,同時(shí)檢查歸來(lái)的患者與新到患者交叉接受診治。
4.服務(wù)臺(tái)與服務(wù)時(shí)間
專家門診的醫(yī)生可視為服務(wù)臺(tái)。為單個(gè)顧客提供服務(wù)開(kāi)始到服務(wù)結(jié)束為止的時(shí)間跨度為服務(wù)時(shí)間。在眼科專家門診的診療過(guò)程中,病人的服務(wù)時(shí)間基本穩(wěn)定,其經(jīng)驗(yàn)分布大多近似愛(ài)爾朗分布。
資料來(lái)源
以武漢市某大型綜合性醫(yī)院的眼科專家門診排隊(duì)系統(tǒng)為研究對(duì)象。收集了2011年4月中旬兩個(gè)星期,從周一到周五共10天該眼科專家門診病人的到達(dá)情況。考慮到每天下午4點(diǎn)后專家門診基本上都在處理之前排隊(duì)的病人和預(yù)約病人,因此,每天的觀察時(shí)間為早上8點(diǎn)到下午4點(diǎn)。以患者到達(dá)接診臺(tái)登記等待為標(biāo)志,進(jìn)入排隊(duì)系統(tǒng),結(jié)束服務(wù)離開(kāi)為終止標(biāo)志。共獲得390位就診患者的排隊(duì)數(shù)據(jù)資料。
G/Ek/c模型擬合與參數(shù)估計(jì)
1.G/Ek/c模型擬合
在觀測(cè)的10天共80小時(shí)期間,390位就診患者的到達(dá)率為4.88(人/小時(shí))。其中,到達(dá)的間隔時(shí)間最短為5分鐘,最長(zhǎng)20分鐘,中位數(shù)為12.5分鐘,算術(shù)平均數(shù)為10分鐘。可將病人相繼到達(dá)醫(yī)院眼科專家門診的間隔時(shí)間分布看作一般分布(G)。
對(duì)于病人服務(wù)時(shí)間的分布,介于等長(zhǎng)分布(D)與負(fù)指數(shù)分布(M)之間,即服務(wù)時(shí)間的偏差介于0與1/μ之間〔3,4〕。用來(lái)擬合這類中間情況的理論服務(wù)時(shí)間分布為愛(ài)爾朗分布,具有較好的靈活性〔5〕。事實(shí)上,負(fù)指數(shù)分布和等長(zhǎng)分布就是愛(ài)爾朗分布當(dāng)k=1和k≈∞時(shí)的特例。
所謂愛(ài)爾朗分布,即設(shè)v1,v2,…,vk是k個(gè)相互獨(dú)立的隨機(jī)變量,服從相同參數(shù)kμ的負(fù)指數(shù)分布,令T=v1+v2+…+vk,則T的概率密度函數(shù)為

且t>0,稱T服從k階愛(ài)爾朗分布〔6〕。公式中 k和μ均為正,且k為整數(shù)。它的平均值為1/μ,方差為(1/kμ)2。為此,對(duì)一個(gè)經(jīng)驗(yàn)服務(wù)時(shí)間分布的平均值和方差進(jìn)行估測(cè)后,利用平均值和方差的公式即可用于確定k的整數(shù)值,并使其與估測(cè)值非常接近〔7〕。
由收集的服務(wù)時(shí)間記錄,取μ=1.5(人/小時(shí)),k=2,擬合愛(ài)爾朗分布。結(jié)果表明該眼科專家門診患者服務(wù)時(shí)間的分布服從k=2,均數(shù)為2/3(小時(shí)),方差為1/9的2階愛(ài)爾朗分布(χ2=3.1477,P=0.5334),見(jiàn)表1。因此,可按病人依次到達(dá)間隔時(shí)間服從一般分布G,服務(wù)時(shí)間服從Ek分布進(jìn)行 G/Ek/c模型擬合。

表1 眼科專家門診服務(wù)時(shí)間的2階愛(ài)爾朗分布擬合結(jié)果
2.G/Ek/c模型的參數(shù)
記排隊(duì)系統(tǒng)整個(gè)服務(wù)機(jī)構(gòu)的服務(wù)強(qiáng)度為ρ,是服務(wù)系統(tǒng)的平均利用率,即ρ=λ/cμ。當(dāng)ρ<1時(shí),不會(huì)排成無(wú)限隊(duì)列,系統(tǒng)平均到達(dá)率等于離去率,達(dá)到平衡狀態(tài)。排隊(duì)論模型的求解是基于平衡狀態(tài)下的定量指標(biāo)。主要指標(biāo)如下〔10〕:
λ—系統(tǒng)中新顧客的平均到達(dá)率;
c—服務(wù)臺(tái)數(shù);
μ—整個(gè)系統(tǒng)的平均服務(wù)率;
ρ—服務(wù)強(qiáng)度,即服務(wù)設(shè)施的利用因子,是平均到達(dá)率與平均服務(wù)率之比;
ρ=λ/cμ;
P0—服務(wù)臺(tái)空閑概率;
Pn—系統(tǒng)中有n個(gè)顧客的概率;
Ls—隊(duì)列長(zhǎng),系統(tǒng)中的顧客總數(shù);
Lq—排隊(duì)長(zhǎng),隊(duì)列中正在排隊(duì)等待的顧客數(shù);
Ws—逗留時(shí)間,顧客在系統(tǒng)中的停留時(shí)間,包括等待時(shí)間和服務(wù)時(shí)間;
Wq—等待時(shí)間,顧客在隊(duì)列中的等待時(shí)間;
相關(guān)指標(biāo)相互關(guān)系的Little公式:

3.G/Ek/c模型參數(shù)估計(jì)
G/Ek/c模型的參數(shù)估計(jì)較復(fù)雜,國(guó)內(nèi)尚無(wú)詳細(xì)的文獻(xiàn)介紹。目前,國(guó)外文獻(xiàn)報(bào)道了幾種不同的解法,主要采用近似的逼近法〔8-9〕,基本求解過(guò)程如下〔10〕。
設(shè)排隊(duì)系統(tǒng)在穩(wěn)定狀態(tài)下,n為在時(shí)間x系統(tǒng)中的人數(shù),l為在時(shí)間x到達(dá)的人數(shù),i為系統(tǒng)中正在接受服務(wù)的人數(shù),s為在服務(wù)的服務(wù)臺(tái)數(shù),在時(shí)間x有顧客n個(gè)的概率為P,則有

公式中a(s,m)為線性方程,wj是方程的根,且Bj和wj滿足如下方程:

在采用FCFS規(guī)則下,假設(shè)新到顧客的平均等待時(shí)間為:
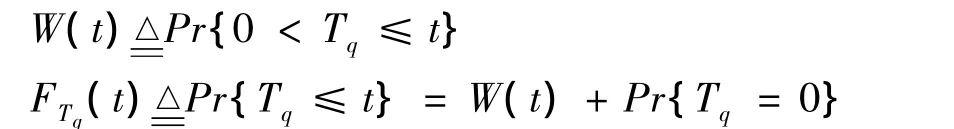
模型在穩(wěn)定狀態(tài)下,解以上方程,平均等待時(shí)間近似為


由解得的Lq和Wq,根據(jù)Little公式〔6〕,其它指標(biāo)也就可以計(jì)算出來(lái)了。
結(jié) 果
基于 λ =4.88(人/小時(shí)),μ =1.5(人/小時(shí)),k=2,對(duì)該眼科門診的坐診專家人數(shù)c為3人、4人和5人時(shí),應(yīng)用 G/Ek/c模型,利用軟件 Open Office加載QtsPlus4Calc〔3-4〕計(jì)算得各項(xiàng)主要評(píng)價(jià)指標(biāo),如表 2 所示。并以系統(tǒng)中的病人數(shù)為橫坐標(biāo),相應(yīng)的概率為縱坐標(biāo),在c=3,c=4時(shí)繪制概率圖,如圖1和圖2所示。

表2 G/Ek/c模型應(yīng)用的參數(shù)估計(jì)結(jié)果

圖1 c=3時(shí)系統(tǒng)中病人數(shù)的概率圖
由以上結(jié)果可知,當(dāng)有3位專家坐診時(shí),系統(tǒng)利用率為98.84%,平均每小時(shí)系統(tǒng)空置的概率為0.0013,隊(duì)列中平均每小時(shí)19.96人,排隊(duì)人數(shù)平均每小時(shí)16.99人,病人平均排隊(duì)等待時(shí)間為3.54小時(shí),且隊(duì)列中大于10人的概率為0.6868。表明擁擠現(xiàn)象很嚴(yán)重。
如增加1位坐診專家,即當(dāng)c=4時(shí),系統(tǒng)利用率為82.50%,平均每小時(shí)系統(tǒng)空置的概率為0.0040,隊(duì)列中平均每小時(shí)4.14人,排隊(duì)人數(shù)平均每小時(shí)不足1人,病人平均排隊(duì)等待時(shí)間為0.17小時(shí),且隊(duì)列中有10人的概率降為0.0262。擁擠情況已經(jīng)大為改善,效果相當(dāng)明顯,基本解決了擁擠排隊(duì)的問(wèn)題。
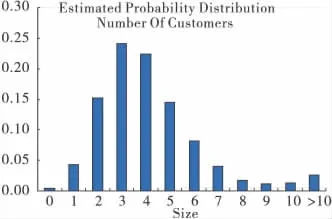
圖2 c=4時(shí)系統(tǒng)中病人數(shù)的概率圖
如增加2位坐診專家,即當(dāng)c=5時(shí),系統(tǒng)利用率為66.71%,平均每小時(shí)系統(tǒng)空置的概率為0.0221,隊(duì)列中平均每小時(shí)3.52人,排隊(duì)人數(shù)平均每小時(shí)0.17人,病人平均排隊(duì)等待時(shí)間為0.04小時(shí),已經(jīng)完全不存在排隊(duì)擁擠的現(xiàn)象了。但相對(duì)4位專家的情況下,改善效果并沒(méi)有明顯增大,相對(duì)很高的人力成本來(lái)說(shuō),呈現(xiàn)出了浪費(fèi)。
綜合而言,該醫(yī)院眼科專家門診安排4位專家坐診較為合理。
討 論
到醫(yī)院就診排隊(duì)是一種司空見(jiàn)慣的現(xiàn)象,我國(guó)由于醫(yī)療行業(yè)資源不夠充分,這一現(xiàn)象顯得更為突出。如果盲目增加服務(wù)窗口,包括配置人員或者相應(yīng)的醫(yī)療設(shè)備,可能發(fā)生空閑和浪費(fèi)。如果服務(wù)窗口配置不足,容易導(dǎo)致病人因排隊(duì)時(shí)間太長(zhǎng)而產(chǎn)生抱怨、不滿、憤怒等負(fù)面情緒,甚至在排隊(duì)過(guò)程中出現(xiàn)不良后果,對(duì)醫(yī)院的滿意度下降,直接影響病人對(duì)醫(yī)院的選擇和醫(yī)院的品牌及整體管理質(zhì)量。
本研究通過(guò)觀察醫(yī)院眼科專家門診的排隊(duì)狀況,引入G/Ek/c排隊(duì)論模型,對(duì)其人力資源配置進(jìn)行評(píng)價(jià)和預(yù)測(cè),為提高醫(yī)院的服務(wù)效率,優(yōu)化醫(yī)療資源配置提供了科學(xué)的參考依據(jù)。
1.王瑩.排隊(duì)論模型求解就醫(yī)排隊(duì)問(wèn)題.科技資訊,2010,(17).
2.Vasanawala SS,Desser T S.Accommodation of requests for emergency US and CT:applications of queueing theory to scheduling of urgent studies..Radiology,2005,235(1):244-249.
3.周文正,尹平,馬玉全,等.排隊(duì)論模型M/D/c在醫(yī)療服務(wù)系統(tǒng)中的應(yīng)用.中國(guó)衛(wèi)生統(tǒng)計(jì),2009,26(6):608-610.
4.周俊,周文正,尹平.G/M/c模型在醫(yī)院口腔科門診診療系統(tǒng)中的應(yīng)用.中國(guó)醫(yī)院統(tǒng)計(jì),2010,17(2):135-138.
5.Rosenquist C J.Queueing analysis:a useful planning and management technique for radiology..JMed Syst,1987,11(6):413-419.
6.Frederick S.hillier,Gerald J.Lieberman.運(yùn)籌學(xué)導(dǎo)論.第八版.胡運(yùn)權(quán)譯.北京:清華大學(xué)出版社,2007,774-777.
7.Gorunescu F,Mcclean SI,Millard PH.Using a queueing model to help plan bed allocation in a department of geriatric medicine.Health Care Manag Sci,2002,5(4):307-312.
8.Avis D.Computing waiting times in GI/E ~ /s queueing system,TIMS Studies in Management Science,1977,7:215-232.
9.Ishikawa A.Stationary waiting time distribution in a GI/Ek/m queue,Oper.Res.Soc.Japan 27,1984:130-149.
10.Bertsimas D.An exact FCFSwaiting time analysis for a general class of G/G/s queueing systems.Queueing Systems 3,1988:305-320.

