基于EMD的時間序列不同頻率波動及趨勢研究

史美景，曹星婉

（1.西安交通大學 經濟金融學院，西安710061；2.上海財經大學 金融系，上海200433）

0 引言

作為一種非線性非平穩性時變信號處理方法,希爾伯特-黃變換(Hilbert-Huang transform,HHT)[1]已經被廣泛應用到地震、大氣科學、氣象、水文地質、生態經濟學和醫學等眾多非線性科學領域，取得了令人矚目的成果。然而，對經濟和金融領域非線性、非平穩時間序列的應用還很少見。Huang，Wu和Qu[2]首次應用HHT的經驗模態分解（Empirical Mode Decomposition，EMD）方法分析金融時間序列波動，提供了一種新的分析非線性、非平穩序列的統計分析工具，之后少有經濟和金融領域的應用研究結果出現。我國已有個別學者把EMD法應用于經濟金融領域，秦宇[3]應用EMD法對上證指數日收益率序列進行趨勢和分解波動分析；陳成忠和林振山[4]利用EMD分解方法對我國CPI波動周期即驅動因素進行分析；劉海飛，李心丹[5]對上證指數收益率利用EMD進行分析，發現該方法較小波分析方法擬和精度更高、預測功能很強。

針對HHT的EMD法在處理非線性、非平穩序列不同頻率的特征，本文將嘗試利用該方法對我國通貨膨脹率和股票收益率波動及趨勢進行分析。雖然HP濾波法已經是研究經濟和金融時間序列波動的主要方法，但HP法存在一個主觀選取的參數，如果單位根存在還可能產生虛假頻率。小波分析也能用來分析時間序列的周期波動，但它也只能處理簡單的線性系統的非平穩過程。因此本文將利用經驗模式分解EMD法研究通貨膨脹率和真實股票收益率的不同時間尺度、不同頻率的波動關系，意在更深入了解股票市場的波動特點以及宏觀經濟變量的關系。

1 EMD方法介紹

希爾伯特-黃轉換（HHT）由臺灣中央研究院黃鍔院士引進，是一種適于分析非線性與非平穩時間序列的方法。該轉換包含兩個部分，第一個部分是經驗模態分解（EMD），第二部分是希爾伯特轉換。不同于傳統的濾波器，EMD是一種從實驗數據中獲取波動韻律的有效方法，此優點使研究人員較容易對時間序列給出解釋。

HHT的EMD是基于任何時間序列的，由簡單振蕩的本質模態IMF組成的，其基本概念是以實驗數據本身的特征時間尺度來分解數據，因此，分解便是適應性的。EMD分解的過程是利用篩選資料的方式來產生IMF，所得的IMF是一組表現良好的本質模態，其相對于平均值是對稱的，并且具有相同的極值與跨零數目。因此，所有的IMF函數，其波形局部對稱于零平均值，都具有良好的希爾伯特轉換，可以求得有意義的瞬時頻率。

EMD產生IMF的算法相當簡單，主要包含兩個步驟：

步驟一：找出實驗數據x(t)中局部的極值，并以立方樣條曲線連接這些局部的極值，其中局部極大值的連線形成上包絡線U(t)，局部極小值的連線形成下包絡線L(t)，兩包絡線包住所有資料點。上下包絡線的平均值m1(t)為：

將原始數據資料x(t)減去平均值m1(t)，我們可以得到一個分量h1(t):

如果所得的分量h1(t)是對稱的，且所有局部極大值均為正值而所有局部極小值均為負值，則其為IMF。如果h1(t)不是一個IMF，則重復上面的步驟直到擷取出來的信號是IMF。在這個過程中，h1(t)將被當作是原始資料并重復步驟。

如果函數h11(t)仍不滿足IMF的要求，則重復上述步驟k次直到所得的函數滿足某一可以接受的誤差，結果：

步驟二：若所得的時間序列是IMF，則將其標示為c1=h1k(t)。接著把原始資料減去第一個IMF，所得之差為：

r1，為一殘差值。將r1當作原始數據，我們可以再一次運用上述步驟一的程序。按照步驟一與步驟二的程序，我們持續找到更多的IMF直到最后一個。最后的殘差值是一個常數或是單調的趨勢。如此，可以得到原始訊號x(t)可以表示成n個IMF分量ci(i=1～n)與一個平均趨勢分量rn的組合，亦即:

2 實證分析

2.1 通貨膨脹率和股票收益率的IMF分量

通貨膨脹率的度量采用樣本期為1991年1月至2011年6月的我國居民消費價格CPI月度同比增長數據x1(t)，股票市場收益率度量采用同期上證綜合指數實際收益率數據x2(t)，實際收益率=名義收益率-通貨膨脹率，其中名義收益率為每月收盤價的對數差分。

圖1 CPI序列、CPI的IMF分量以及趨勢

圖2 上證指數收益率序列、IMF分量以及趨勢

把x1(t)和x2(t)當作原始數據，并應用EMD將它們分解成6個IMF（計算機自動生成，MATLAB編程），圖1是x1(t)的EMD分解結果，Ci(i=1～6)是篩選出來的IMF分量；圖2是x2(t)的EMD分解結果，Ri(i=1～6)是篩選出來的IMF分量。應注意的是，經由EMD分解的IMF的數量與原始時間序列的特性有關。從這些IMF的性質，可以了解分解的實際意義。首先我們比較圖中的時間序列x1(t)與從x1(t)分解出來的每一個IMF都是獨立的，且各個IMF之間互相正交。IMFC1到C6的主要差異在于其各自的頻率范圍不同，C1是在篩選過程中從x1(t)分離的第一個分量，其具有6個IMF中最高的頻率；C6是最后一個分量具有最低頻率。因為時間序列x1(t)的細部結構是由最高頻率的分量來描述，因此C1抓住了收益率時間序列x1(t)的高頻波動特征，而C6反映了最低頻率波動特征。最后的小圖是原序列剔除所有IMF分量和的剩余部分，實際上是原始序列CPI的平均趨勢部分。

此外，比較相同階數（order）的IMF，可以更清楚地看到CPI序列和收益率時間序列的關聯行為。既然IMF的平均頻率與其階數成反比（C1的頻率比C6的頻率高），我們可以對相同階數的IMF分析兩者之間的關聯行為。這有助于了解兩個序列的相關程度與時間尺度之間的關系。

對上證綜合指數的月收益率時間序列同樣應用EMD將其分解成若干個IMF，結果如圖所示，其中收益率時間序列也被分解成6個IMF。在這些IMF中，第一個IMF分量R1具有最高頻率，最后一個IMFR6具有最低頻率，分別顯露金融時間序列的高頻波動和低頻波動的隨機性質。第一個IMF抓住波動的細部結構，對金融時間序列而言，這些波動特征是隨機的，也是不可預測的。在這個時間尺度下，波動振蕩基本上是由局部（區域性）的交易活動決定，即由個別的買賣效應主導。相反地，高階低頻的IMF可以看成是原來時間序列的局部平均，其中小時間尺度的波動已經被“抹平”。“抹平”的效果類似于以某一窗口大小對原來的時間序列取平均。在此情況下，宏觀經濟狀況、政府的政策與其它平衡機制可能是決定時間序列較大尺度行為的主要因素。最后一個小圖顯示樣本期內上證指數實際月收益率波動的平均趨勢特征。

對比兩序列的最后一個IMF分量C6和R6，它們是代表樣本期內長周期波動，CPI呈現出U型波動特征，在中國經濟快速發展的二十年間，前十年通貨膨脹率一直在高位運行，2001年左右見底，后十年處于整個波動的上升期。而股票實際收益率呈現出N型特征，股票實際收益率在1994年8月左右達到最低點，因為在1994年7月底股市跌至333.92，證監會出臺“停發新股、允許券商融資、成立中外合資基金”三大政策救市，此點位成為中國股市發展至今的最低點。而同期通貨膨脹率達到25.8%，幾乎接近10月的歷史最高點（27.7%），致使股票的實際收益達到歷史最低點，與實際情況的分析完全一致。另外，兩者的反向相關系數達到0.422，通貨膨脹率在2001年上半年見底，股市實際收益率在2003年10月見頂，從整個樣本期來看通貨膨脹率波動領先股市兩年反轉。

為了進一步了解EMD分解的特征，對IMF分量從低階向高階疊加。圖3～6是把分解后的各個IMF逐階疊加，圖3是CPI的低頻長周期波動部分；圖4和圖5分別是C3～C6的疊加，C2～C6的疊加；圖6的C1到C6是CPI增長率所有頻率波動的和，是去除趨勢的周期波動，如果再加上趨勢變動部分就完全與CPI原序列重合（圖略）。實際上EMD分解就是把一個非平穩、非線性的序列分解為若干個平穩的不同頻率或周期的分量以及一個趨勢的過程。

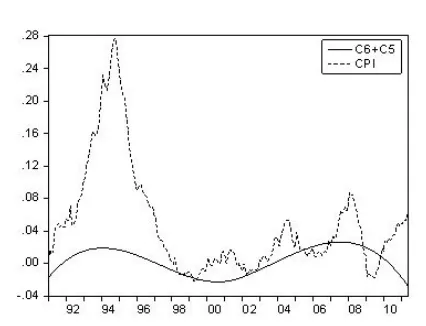
圖3 CPI和EMD分解的

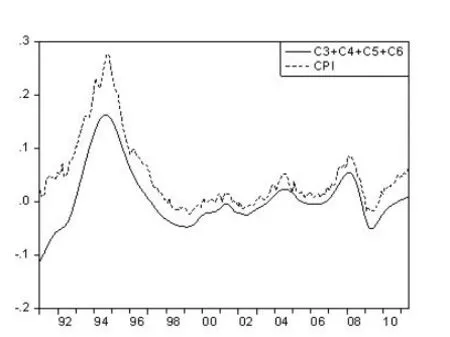
圖4 C3-C6的疊加

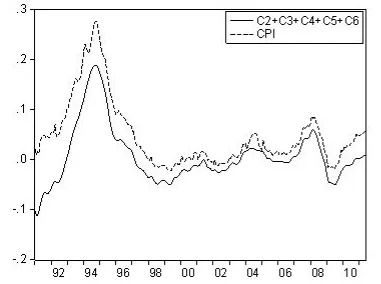
圖5 C2—C6的疊加

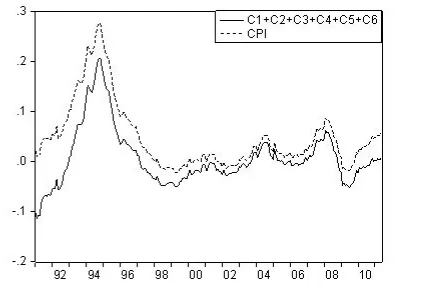
圖6 C1—C6疊加

2.2 通貨膨脹率和股票收益率的不同周期波動及相關性分析

此外，比較相同階數（order）的IMF，可以更清楚地看到CPI序列和收益率時間序列的關聯行為。既然IMF的平均頻率與其階數成反比（C1的頻率比C2的頻率高），我們可以對相同階數的IMF分析兩者之間的關聯行為。這有助于了解兩個序列的相關程度與時間尺度之間的關系。為了更清楚的觀察不同頻率的關聯行為，根據我國通貨膨脹率和股市時間序列波動的特征，把波動過程分為短周期（高頻）、中周期（中頻）、長周期（低頻），即把6階IMF合并為高（1、2階）、中（3、4階）、低（5、6階）三個頻率等級。一般高頻率特征反映的是時間序列瞬時噪聲和不規則影響因素部分，中周期中頻率可能含有季節變動因素，而長周期則反映宏觀經濟變動以及上市公司基本面的影響。本研究主要關注中周期和長周期的波動特征，中周期兩序列分別用C34和R34表示，長周期低頻率波動分別用C56和R56表示。圖7、圖8顯示了它們之間的關系。

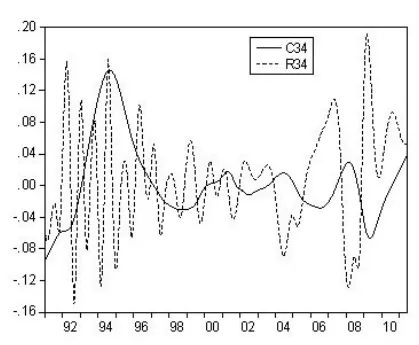
圖7 兩序列中周期相關性

圖8 兩序列長周期相關性

從圖7發現樣本期內CPI中周期頻率明顯有五個波谷分別是1991年1月、1998年9月、2002年7月、2006年7月和2009年5月；有四個波峰分別是1994年10月、2001年5月、2004年6月和2008年3月，與實際情況基本一致。每兩個波谷之間時間間隔依次為：92個月、46個月、48個月和34個月；每兩個波峰之間的時間間隔依次為：92個月、37個月和45個月。20世紀90年代初期我國出現了經濟過熱現象，引發了一輪嚴重的通貨膨脹，CPI增長率在1994年10月達到歷史高點。在惡性通脹階段，過度的通脹應對股市具有較強的抑制作用，因為高通脹造成企業高成本，從而使上市公司經營困難，公司股票下跌；高通脹必然引起管理層不斷推出十分嚴厲的從緊政策治理通脹，政策不僅制約了經濟發展，也有可能造成股市的下跌；另外，高通脹造成實際的負利率，會促使銀行利率不斷上調，造成企業資金緊張和股市資金困難，有可能引起股市下跌。但是，在1997年前我國股票市場剛開始建立，政策法規不夠健全、供求結構關系失衡、投資者過度投機并且市場沒有漲跌停板的限制導致股市劇烈波動，尤其在94年左右的高通脹期，并沒有出現股市的大跌現象，負向相關關系不明顯。但在后期，隨著股市供求關系逐漸達到均衡，投資者更加趨于理性，通貨膨脹率波動和股市波動負向共變性越來越明顯。2002年后幾乎每個CPI的波峰都對應著股票收益率序列的波谷，每個CPI的波谷都對應著股票收益率序列的波峰，顯著存在負向共變性。圖8顯示的是兩序列低頻率長周期波動關系，通貨膨脹率波動呈現M型，股市實際收益率在1997年后趨于平緩，近些年處于下降趨勢。

為了更深入了解通貨膨脹率與股市波動之間的關系，利用交差相關系數計算兩序列不同的滯后期和領先期之間的相關系數，檢驗通貨膨脹率和股市收益率之間的領先滯后關系。

從表1可發現：①通貨膨脹波動和股市收益率波動均呈現負向相關關系，但是相關程度都不高，相關系數均小于0.5。②頻率越高相關程度越低，高頻率低周期的兩序列相關系數都不顯著。③中周期C34和R34(-i)的相關程度弱于同期相關性0.128，而C34和R34(+i)的相關程度強于同期相關性0.128，說明通貨膨脹率波動略為領先股票收益率波動，領先大約3到5個月。④從長周期的情況來看，和中周期相似，C56和R56(-i)的相關程度弱于同期相關性0.329；C56和R56(+i)相關程度強于同期相關性0.329，通貨膨脹率波動略為領先股票收益率波動，領先大約7到8個月。中長期來看，通貨膨脹率波動是股票收益率波動的影響因素，為了更進一步證實這個結論還要通過Granger因果檢驗證實兩者的因果關系。

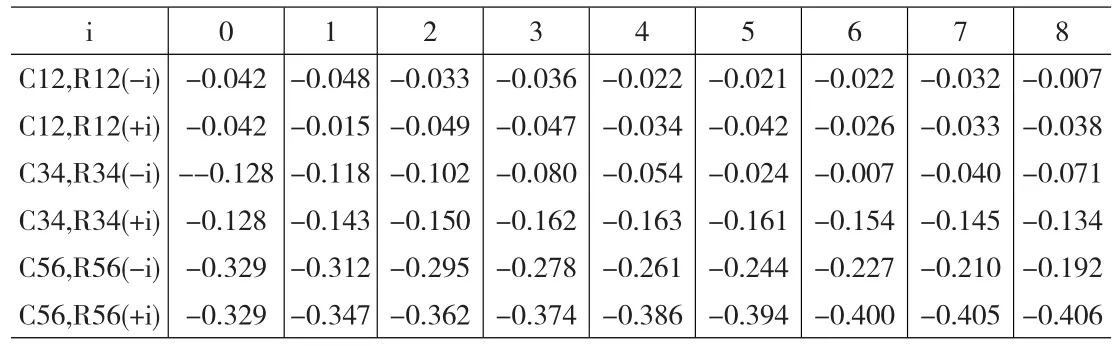
表1 兩序列不同周期的交叉相關系數

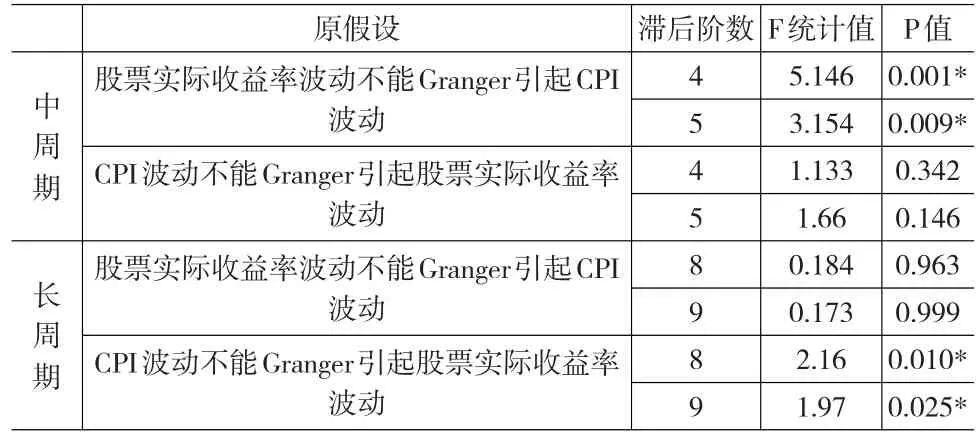
表2 兩序列中、長周期波動的Granger因果檢驗

表2結果說明，從中周期看通貨膨脹不是股票實際收益率變動的Granger因果關系，反之，股票收益率波動引起CPI的波動，滯后期為4到5個月，這個結果與交叉相關系數分析的結果不一致。從長周期看CPI波動能Granger引起股票實際收益率波動，領先大約8到9個月，與上述分析結果一致，也即當通貨膨脹到達波峰或波谷后大約9個月后，股票收益率到達波谷或波峰，進入牛市周期或熊市周期。

2.3 通貨膨脹率和股票收益率波動的趨勢分析

社會、經濟現象的發展主要是漸進型的，其發展相對于時間具有一定的規律性。因此當預測序列隨時間變化呈現某種上升或下降的趨勢，并且無明顯的季節波動，周期波動，又能找到一條合適的函數曲線反映這種變化趨勢時，就可以建立一時間為自變量的趨勢模型。

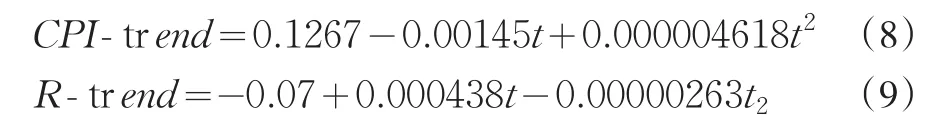
EMD分解能夠得到序列的趨勢變動分量，公式（6）的rn是剔除了所有波動的平均趨勢分量，圖1和圖2中最后的小圖分別是CPI趨勢CPI_TREND和股票實際收益率趨勢R_TREND的圖型，圖9是兩者的比較，圖10是CPI原序列和趨勢變動。經擬合CPI趨勢與股票實際收益率趨勢都是二次拋物線，擬合優度均達到100%，是完全擬合。不同的是CPI的長期趨勢變動是開口向上，股票實際收益率變動長期趨勢是開口向下，再次證實兩者的反向相關性，目前通貨膨脹正處于上升階段，而股票收益率則處于下降階段，與實際情況非常吻合。

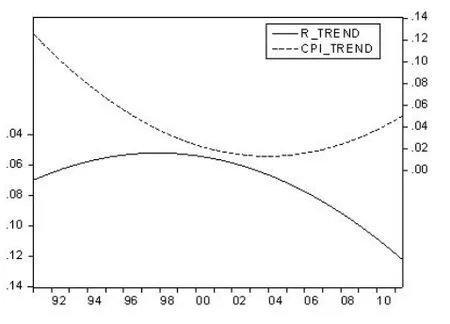
圖9 CPI趨勢和股票實際收益率趨勢

圖10 CPI原序列和趨勢變動

3 結論

希爾伯特-黃轉換（HHT）的EMD法為分析經濟金融領域的非線性和非平穩時間序列不同周期的波動以及序列的變動趨勢提供了一種新的統計分析工具。本文利用這種新的分析方法對我國通貨膨脹率以及股票實際收益率的不同頻率、不同周期波動和長期變動趨勢進行了實證分析，并檢驗了兩者之間的相互影響關系。研究發現：①不同頻率兩序列都存在反向相關關系，但頻率越低波動的反向相關性越顯著，即長周期波動的負相關性更明顯，長期投資股票市場并不能夠對沖通貨膨脹的上漲。②二十年的樣本期來看，中長期來看，通貨膨脹率波動領先股市波動平均大約為8個月。整個樣本期內通貨膨脹率呈現U型波動特征，股票實際收益率波動呈現N型特征，兩者呈現顯著的反向相關性。中長期來看，投資股市無法對沖通貨膨脹的上漲。③HHT的EMD法最大的特點是可以從任何序列中分解出一個趨勢函數。CPI的長期平均趨勢和股市實際收益率的長期平均趨勢均以開口向上、向下的二次拋物線形式變動，根據趨勢外推預測未來的走勢，短期內CPI趨勢仍將向上，股票實際收益率仍將減少。

因此，根據以上分析能夠通過觀察國際大宗商品的價格走勢影響下和宏觀調控下的通貨膨脹率的波動和趨勢變動，調整對股票的投資策略。

[1]Huang,N.E.,Z.Shen,S.R.Long,et al.The Empirical Mode Decom?position and Hilbert Spectrum for Nonlinear and Nonstationary Time Series Analysis[J].Proceedings of the Royal Society Land A,1998，(454).

[2]Huang N.E.，Man-Li Wu,Wendong Qu,et al.Applications of Hil?bert-Huang Transform to Non-Stationary Financial Time Series Anal?ysis[J].Applied Stochastic Models in Business and Industry,2003，(19).

[3]秦宇.應用經驗模態分解的上海股票市場價格趨勢分解及周期性分析[J].中國管理科學,2008，（10）.

[4]陳成忠，林振山.中國居民消費價格指數波動的周期性及其驅動因素研究[J].經濟問題探索,2008，(8).

[5]劉海飛，李心丹.基于EMD方法的股票價格預測[J].統計與決策, 2011,l（10）.

[6]Fama,E.Stock Returns,Real Activity,Inflation,and Money[J].Ameri?can Economic Review,1981，(71).