具密度依賴脈沖出生階段結構單種群動力學模型研究
周玉梅,焦建軍
(貴州財經大學數學與統計學院,貴陽 550004)
0 引言
脈沖微分方程是20世紀60年代迅速發展起來的一個數學分支。脈沖微分方程是微分方程理論研究中的一個重要課題,廣泛用來刻畫生物種群系統的很多現象,例如動物的季節性出生,森林管理和漁業養殖中的種植,投放和收獲等。脈沖微分方程理論在文獻[1]中有詳細的介紹.近幾年在種群生態方面有大量應用[1~6]。
如果考慮生物種群的出生是密度依賴脈沖出生
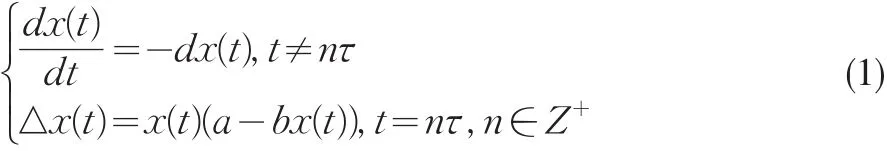
其中,x(t)表示種群密度,a>0是種群出生的內稟增長率.b>0且是種群的出生容納量系數,d是種群的死亡系數,τ是種群的脈沖出生周期。而基本的階段結構種群模型[4]為:
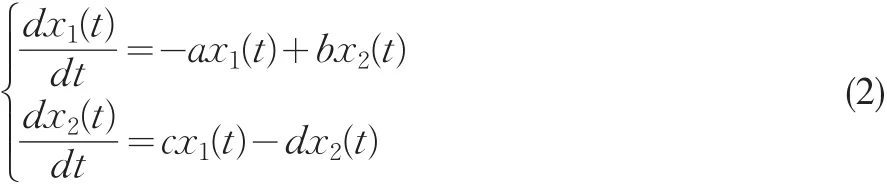
其中,x1(t)與x2(t)分別表示種群幼體與成體的密度. a>c>0且a=c+c1,c>0是種群幼體向成體轉化的系數. c1>0是種群幼體的死亡系數,d>0是種群成體的死亡系數,b>0是種群成體的出生率系數。
1 模型
基于上面的討論,建立具密度依賴脈沖出生階段結構單種群動力學模型:

其中,x1(t)與x2(t)分別表示種群幼體與成體的密度,a>0是種群的脈沖出生系數,d>0是種群幼體的死亡系數,c>0是種群幼體向成體轉化的系數,d>0也是是種群成體的死亡系數,在t=nτ時刻種群脈沖出生,τ是種群的脈沖出生周期。
2 動力學分析
設 x(t)=(x1(t),x2(t))T是一個分段連續函數 x:R+→,它是(3)的解,x(t)在區間(nτ,(n+1)τ]上連續,且x(t)存在。顯然,(3)的右邊函數的光滑性保證了其解的全局存在性和唯一性[1]。
由系統(3)的第一與第二個方程,容易得到系(3)在脈沖點之間的解析解:
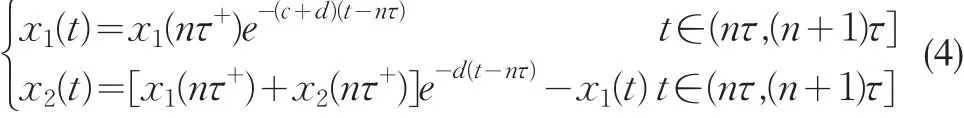
由系統(3)的第三個方程與第四個方程,得到系統(3)的頻閃映射:
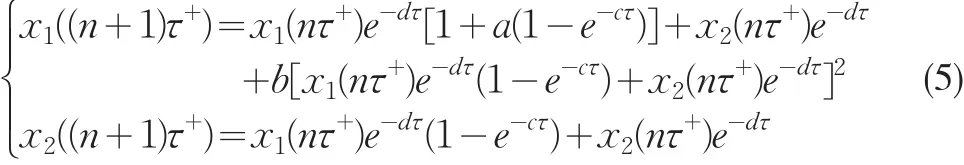
做記號A=e-dτ(1-e-cτ),B=e-dτ,且0<A<1,0<B<1,那么(5)可以改寫為:
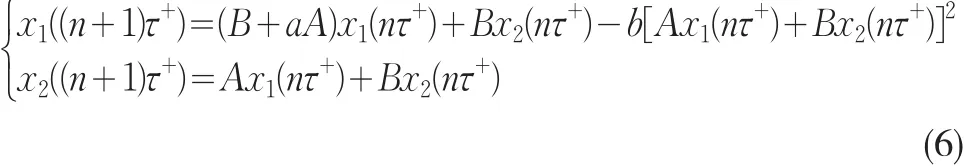
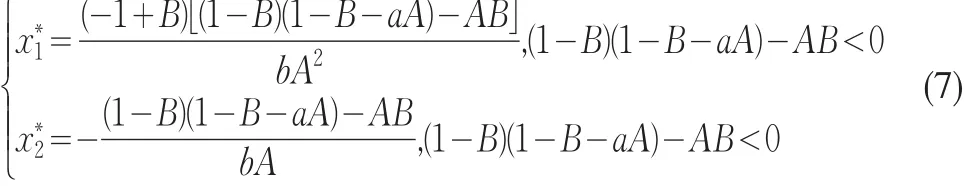
定理1(1)當(1-B)(1-B-aA)-AB>0時,差分系統(6)的不動點P(0,0)是全局漸近穩定的;
(2)當(1-B)(1-B-aA)-AB<0時,差分系統(6)的不動點P*(,)是全局漸近穩定的‘

顯然P(0,0)或P*(,)附近的動力學性態可以由(6)的線性系統(8)來決定,M作為(6)的線性系統(8)對應矩陣;P(0,0)或P*(,)的穩定性由M的特征值小于1決定。當M滿足下列的Jury判據條件時,可知M的特征值小于1[5]:

(1)當(1-B)(1-B-aA)-AB>0時,P(0,0)是差分方程(6)的唯一平衡點。于是得到

由Jury判據條件1-trM+detA=(1-B)(1-B-aA) -AB>0可知,平衡點P(0,0)是局部穩定的,從而是全局漸近穩定的。
(2)當 (1-B)(1-B-aA)-AB<0時,顯然平衡點P(0,0)是不穩定的。由于(1-B)(1-B-aA)-AB<0,所以存在正平衡點P*(,),且有
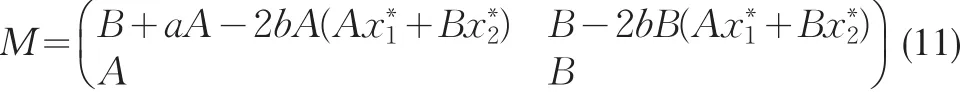
于是
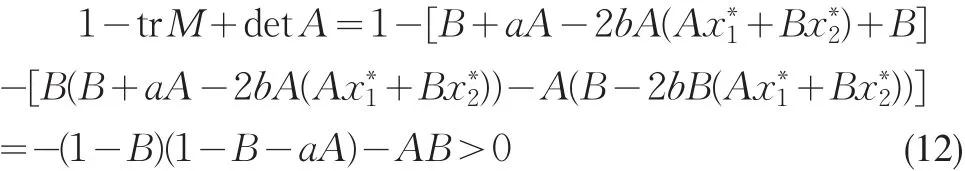
根據Jury判據可得平衡點P*(,)是局部漸近穩定的,從而是全局漸近穩定的。證畢。
根據定理1易得:
定理2(1)當(1-B)(1-B-aA)-AB>0時,系統(3)的平凡周期解(0,0)是全局漸近穩定的;
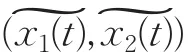

3 討論
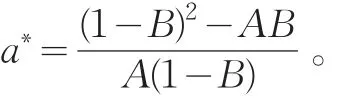
[1]V.Lakshmikantham,D.D.Bainov,P.Simeonov.Theory of Impulsive Differential Equations[M].Singapore:World Scientific,1989.
[2]JIAO,J.,Yang,X.,Chen,L.,Cai,S.Effect of Delayed Response in Growth on the Dynamics of a Chemostat Model with Impulsive Input [J].Chaos,Solitons and Fractals,2009,(42).
[3]Jiao Jianjun,Chen Lansun.Global Attractivity of a Stage-structure Variable Coefficients Predator-prey System with Time Delay and Impulsive Perturbations on Predators[J].International Journal of Biomathematics,2008,1(2).
[4]Jiao Jianjun,Chen Lansun,Long Wen.Pulse Fishing Policy for a Stage-structure Model with State-dependent Harvesting[J].Journal of Biological System,2007,(4).
[5]E.L.Jury.Inners and Stability of Dynamics System[M].New York: Wiley,1974.
[6]于法穩.貴州省農業可持續發展優勢分析及對策研究[J].貴州財經,2012,30(2).

