用中考的眼光審視相似三角形的教學

?五常市萬寶中學 劉 玉

相似三角形是初中幾何的一個重要內容，學好相似三角形不僅能使我們對圖形相似有更深刻的認識，也能使我們以前學過的全等三角形的知識得以鞏固和提高.正是由于相似三角形具有很強的綜合性，在各種考試中，常常以圖形的相似，尤其是相似三角形的知識點進行考查.

一、中考命題趨勢

相似三角形在近年來各省、市的中考試題中所占的比例較高，主要考查三角形相似，線段的倍分，及等積式、等比式，求線段的比、面積的比等.其中求線段的比、面積的比，常以選擇題、填空題的題型出現(xiàn)；論證線段的倍分、等積式、等比式，常以證明和說理題型出現(xiàn)；以相似圖形為背景，探究函數(shù)解析式及其函數(shù)最值等問題，常以解答題的形式出現(xiàn)，這種題型知識性、綜合性強，方法靈活，常以此來構筑中考壓軸題.

二、中考復習建議

1.注重基礎知識.本部分的重點是相似三角形的判定與性質，應用相關定義和定理進行證明是本部分知識的難點.復習時教師要注意引導學生分析證明思路，引導學生進行轉化，幫助學生克服難點.

2.注意聯(lián)系實際.相似是生活中常見的現(xiàn)象，在復習中，要通過復習相似的相關知識，從實際生活中發(fā)現(xiàn)數(shù)學問題，運用數(shù)學知識解決實際問題.

3.重視知識間的聯(lián)系.在中考綜合題中，經(jīng)常涉及有關相似的內容，所以在復習中，要注意把相似與圓、函數(shù)等內容聯(lián)系起來.

4.重視數(shù)學思想方法的滲透.本部分主要涉及的數(shù)學思想方法有類比、轉化、分類討論等，復習時要充分注意數(shù)學思想方法的滲透.

5.把握好復習難度.復習時不要過分追求難題的訓練，要注重基礎知識的理解和掌握，根據(jù)學生掌握知識的實際情況，由易到難，循序漸進.

三、中考考點透視

考點1：考查三角形相似

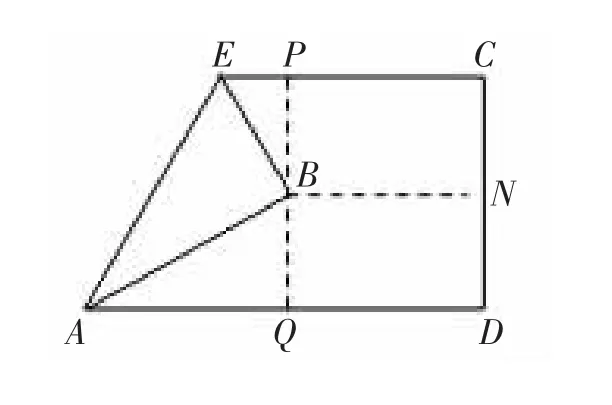
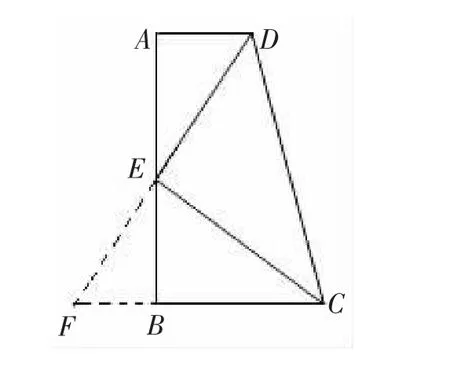
如下圖，先把一矩形ABCD紙片對折，設折痕為MN，再把B點疊在折痕線上，得到△ABE.過B點折紙片使D點疊在直線AD上，得折痕PQ.

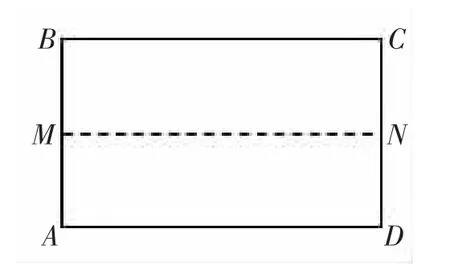
（1）求證：△PBE∽△QAB；

（2）你認為△PBE和△BAE相似嗎？如果相似給出證明，如果不相似，請說明理由；

（3）如果沿直線EB折疊紙片，點A是否能疊在直線EC上？為什么？

分析：（1）利用有兩個角對應相等的兩個三角形相似可以證明△PBE∽△QAB；（2）△PBE和△BAE中，有一對相等的角即∠ABE＝∠BPE＝90°，只要再證得兩個三角形夾相等角的兩邊對應成比例即可.

證明：（1）∠PBE+∠ABQ＝180°-90°=90°，

∵∠PBE+∠PEB=90°，∴∠ABQ=∠PEB.

又∵∠BPE=∠AQB=90°，∴△PBE∽△QAB.

（2）△PBE和△BAE相似.

∵∠ABE＝∠BPE＝90°，∴△PBE∽△BAE.

（3）如果沿直線EB折疊紙片，點A能疊在直線EC上.

由（2）得∠AEB＝∠CEB，又AB⊥BE，

∴EC和AE能重合，從而點A能疊在直線EC上.

解析：與相似三角形有關的問題，要善于尋找、發(fā)現(xiàn)相等的角.得出兩角相等的有效途徑主要有：公共角相等、對頂角相等、同角（或等角）的余角（或補角）相等、高線（或垂直）有直角相等.另外，應用“兩邊對應成比例且夾角相等的兩個三角形相似”來判定兩個三角形相似時，所需要的對應邊之間的比例式，往往通過證明另兩個三角形相似，根據(jù)相似三角形的對應邊成比例得到.

考點2：考查相似三角形的判定與性質

例2：（1）如下圖，⊙O的直徑AB為10 cm，弦AC為6 cm，∠ACB的平分線交AB于E，交⊙O于D.求弦AD、CD的長.

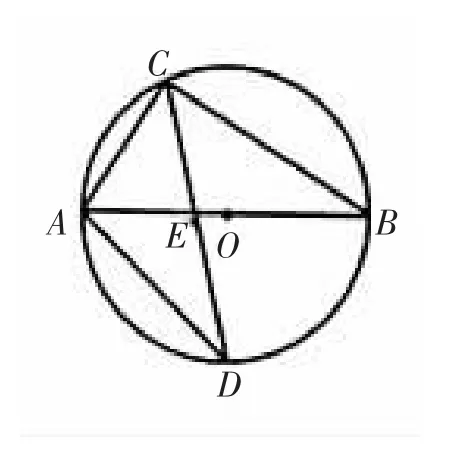
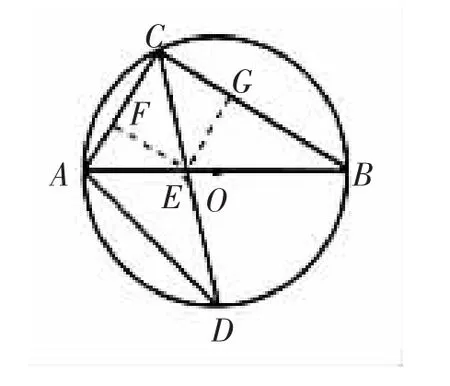
分析：由于AB是⊙O的直徑，∠ACB的平分線交AB于E，所以連接BD后，可知△ABD為等腰直角三角形，從而可求出BD的長.由問題可知，圖形中的所有線段均可求長，由于CD是∠ACB的平分線，所以可通作輔助線構造相似三角形求得AE或BE的長，再利用△DAE∽△DCA或△ACD∽△ECB，或△ADE∽△CBE均可求得CD的長.

解：∵AB是直徑，∴∠ACB=90°.

于是在Rt△ABD中，

如下圖，過E作EF⊥AC于F，EG⊥BC于G，F(xiàn)、G是垂足，

則四邊形CFEG是正方形.

設EF=CF=x，

∴△DAE∽△DCA，

（2）如下頁上圖，在直角梯形ABCD中，AD∥BC，∠B= 90°，E為AB上一點，且ED平分∠ADC，EC平分∠BCD，則下列結論中正確的有（ ）.

A.∠ADE=∠CDE B.DE⊥EC

C.AD·BC=BE·DE D.CD=AD+BC

解析：由ED平分∠ADC可知∠ADE＝∠CDE，故A正確；由AD∥BC得∠ADC＋∠BCD＝180°，又∵∠EDC＝·∠ADC，∠ECD＝∠BCD，∴∠EDC＋∠ECD＝90°，∴DE⊥EC，故B正確；易證△ADE∽△BEC，∴AD∶BE＝DE∶EC，∴AD·EC＝BE·DE，故C不正確；延長DE交CB的延長線于點F，易證△ADE≌△BFE，得AD＝BF，∴CD＝CF＝BC＋BF＝AD＋BC，故D正確.因此，本題應選A、B、D.

解析：本題是一道多選題，是近年來在中考數(shù)學中出現(xiàn)的一種新題型.本題考查的知識點較多，有平行線的性質，角平分線定義，全等三角形的判定和性質，等腰三角形的性質，相似三角形的判定和性質等，能否熟練應用這些定理是解題的關鍵.

考點3：考查相似三角形在位似圖形中的應用

例3：如圖，在8×8的網(wǎng)格中，每個小正方形的頂點叫做格點，△OAB的頂點都在格點上，請在網(wǎng)格中畫出△OAB的一個位似圖形，使兩個圖形以O為位似中心，且所畫圖形與△OAB的位似比為________.

分析：位似圖形一定是相似圖形，但相似圖形不一定是位似圖形.本題可根據(jù)位似圖形及相似三角形的知識求解，應注意所畫三角形的頂點要在格點上.

解：如圖，△OA′B′即為△OAB的位似圖形，位似比為2∶1.

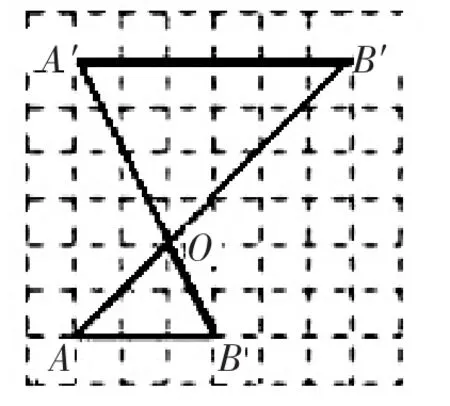
解析：本題考查了位似圖形的概念以及基本作圖。解答時要注意審題，頂點要畫在格點上.需要提醒的是在進行位似變換時，要注意分兩種情況解答：一種是位似圖形有位似中心同側，另一種是位似圖形在位似中心的異側.本題之所以畫△OAB的位似圖形時只畫一個，是因為同側的位似圖形，頂點不在格點上，不合題意，故沒有畫出.

考點4：考查相似三角形中的條件探究型問題

例4：如下圖，在矩形ABCD中，AB＝4，AD＝10，直角尺的直角頂點P落在AD上（點P與A、D不重合），一直角邊經(jīng)過點C，另一直角邊與AB交于點E.（1）當∠CPD＝30°時，求AE的長；（2）是否存在這樣的點P，使△DPC的周長等于△AEP周長的倍整數(shù)？若存在，求出DP的長，若不存在，請說明理由.

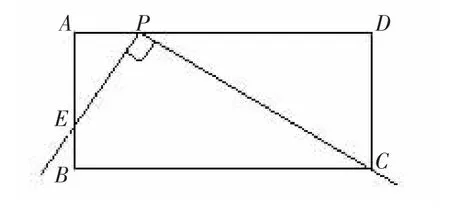
分析：（1）當∠CPD＝30°時，可算出PD、PC的長，后可得AP的長，在Rt△APE中可利用三角函數(shù)或相似求出AE的長；（2）屬于一個條件探究性問題，可先將結論作為條件來探索，如能得到合理的結論，則說明存在，反之則不存在.

解：（1）在Rt△PCD中，

（2）假設存在滿足條件的點P，設DP＝x，則AP＝10-x,由Rt△AEP∽Rt△DPC知=2，所以=2，解得x＝8，此時AP＝2，AE＝4，符合題意.