利用“動態(tài)圓”展示帶電粒子在磁場中的臨界變化
劉月榮
(邗江中學(xué) 江蘇 揚州 225009)
帶電粒子在磁場中臨界問題中大概分為兩類基本問題,一類問題是射進(jìn)磁場的粒子速度方向相同造成的臨界問題;另一類是射進(jìn)磁場的粒子的速度大小相同造成的臨界問題.對于這些兩種問題可以利用“動態(tài)圓”—— 即改變圓半徑的大小或改變圓的位置,從而找出臨界點,進(jìn)一步得出結(jié)論.下面就一些實例對“動態(tài)圓”應(yīng)用作一些詳解.
類型一:射進(jìn)磁場的粒子速度方向相同而速度大小不同造成粒子在磁場中運動的臨界問題——畫出“動態(tài)圓”,改變圓半徑的大小找出臨界條件.
【例1】如圖1所示,真空中狹長區(qū)域的勻強磁場的磁感應(yīng)強度為B,方向垂直紙面向里,寬度為d,速度為v的電子從邊界CD外側(cè)垂直射入磁場,入射方向與CD夾角為θ,電子的質(zhì)量為m、電荷量為q,為使電子從磁場另一側(cè)邊界EF射出,求電子的速度v應(yīng)為多大.(不計電子的重力)
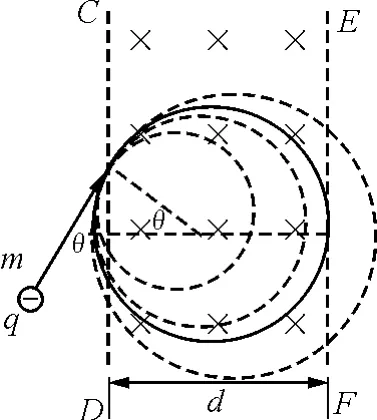
圖1
解析:所有電子射進(jìn)磁場時速度方向與磁場的CD邊成θ角,但粒子的速度大小不同,故粒子在磁場中運動的圓軌跡的半徑不同.改變粒子運動的半徑,畫出粒子運動的軌跡 —— 與入射速度相切的“動態(tài)圓”,如圖1所示.可以看到隨著粒子運動速度的增大,粒子運動的軌跡將會從EF射出.若要使粒子從EF射出,則臨界條件應(yīng)取粒子運動的軌跡與EF相切.設(shè)粒子運動的半徑為R,則
(1)已知這些離子中的離子甲到達(dá)磁場邊界EG后,從邊界EF穿出磁場,求離子甲的質(zhì)量.
(2)已知這些離子中的離子乙從EG邊上的I點

由相應(yīng)的幾何知識可知

由以上各式得

【例2】(2010年高考全國Ⅱ卷第26題)圖2中左邊有一對平行金屬板,兩板相距為d,電壓為U;兩板之間有勻強磁場,磁場應(yīng)強度大小為B0,方向平行于板面并垂直于紙面向里.圖中右邊有一邊長為a的正三角形區(qū)域EFG(EF邊與金屬板垂直),在此區(qū)域內(nèi)及其邊界上也有勻強磁場,磁感應(yīng)強度大小為B,方向垂直于紙面向里.假設(shè)一系列電荷量為q的正離子沿平行于金屬板面,垂直于磁場的方向射入金屬板之間,沿同一方向射出金屬板之間的區(qū)域,并經(jīng)EF邊中點H 射入磁場區(qū)域.不計重力.(圖中未畫出)穿出磁場,且GI長為,求離子乙的質(zhì)量.

圖2
(3)若這些離子中的最輕離子的質(zhì)量等于離子甲質(zhì)量的一半,而離子乙的質(zhì)量是最大的,問磁場邊界上什么區(qū)域內(nèi)可能有離子到達(dá).
解析:(1)已知離子沿平行金屬板做直線運動,故離子所受電場力和洛倫茲力平衡,得
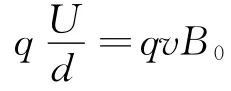
由于離子都是垂直EF邊界進(jìn)入磁場,但由于離子運動半徑無法確定,因此可以改變離子運動的半徑,畫出與離子速度相切的系列“動態(tài)圓”——離子的運動軌跡,如圖2所示.發(fā)現(xiàn)離子若要到達(dá)EG并從EF邊界射出,則離子運動的軌跡圓應(yīng)與EG相切于K點,由幾何關(guān)系得.設(shè)離子運動的半徑為R,則qv B=,得.故得甲離子的質(zhì)量為?

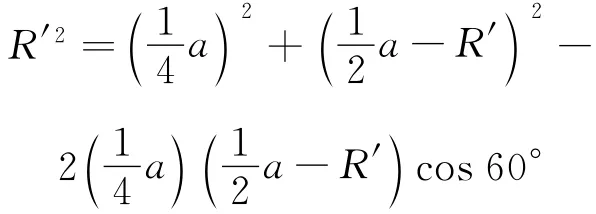
得離子乙的質(zhì)量為

類型二:射進(jìn)磁場的粒子的速度大小相同而方向不同造成粒子在磁場中的臨界問題——利用“動態(tài)圓”,改變圓的位置,找出臨界條件.
【例3】半徑r=10 cm的圓形區(qū)域內(nèi)有勻強磁場,其邊界跟y軸在坐標(biāo)原點O處相切;磁場B=0.33 T垂直于紙面向內(nèi),如圖3所示.在O處有一放射源S可沿紙面向各個方向射出速率均為v=3.2×106m/s的α粒子;已知α粒子質(zhì)量為m=6.6×10-27kg,電荷量q=3.2×10-19C,則α粒子通過磁場空間的最大偏轉(zhuǎn)角θ及在磁場中運動的最長時間t各多少.

圖3

(1)速度大小;
(2)速度方向與y軸正方向夾角正弦.

圖4
解析:由于粒子進(jìn)入磁場的速度大小均相同,故粒子運動的軌跡半徑均相同.粒子進(jìn)磁場的速度方向不同,因此畫出半徑大小相同、但位置不同的“動態(tài)圓”,可從“動態(tài)圓”與磁場的交點看出,軌跡對應(yīng)的弦越長,則圓心角越大,粒子運動的時間越長.故當(dāng)粒子運動軌跡與磁場上邊界相切時,弦最長,圓心角最大,時間最長,最后離開磁場,且時間為運動周期的,故
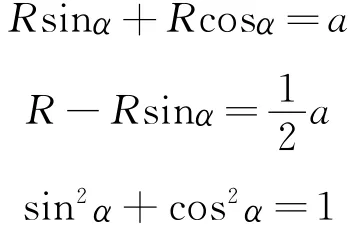
得

通過以上實例對“動態(tài)圓”應(yīng)用的例解,使學(xué)生對此類問題會有很好的把握,提高他們的應(yīng)變能力.

