基于性能參數殘差序列分析的發動機性能衰退研究

譚 巍，李本威，李 冬，王永華

（1.海軍航空工程學院飛行器工程系，山東 煙臺 264001；2.海軍飛行學院，遼寧 葫蘆島 125001）

性能衰退是發動機使用不可避免的過程。對發動機進行性能衰退方面的研究是保證發動機安全工作、發現及排除故障、實現發動機視情維修、延長發動機使用壽命的一種重要技術途徑[1]。

發動機出現性能衰退后，性能參數開始出現緩慢變化，而性能衰退到達一定程度時，很可能會出現較大程度的下降，預示著故障的發生。因此，性能參數的變化包含著發動機性能衰退的許多信息，是發動機性能衰退程度的重要表征。本文通過分析性能參數殘差隨時間的變化規律，進行發動機性能衰退程度方面的研究。

1 數據準備

1.1 參數初選

發動機性能衰退的過程中，氣路部件氣流流通能力和工作效率會逐漸下降，進而造成發動機轉子轉速及氣路中各部件截面的氣流溫度、壓力等征兆參數發生變化。因此，可以通過發動機某一穩定狀態各部件截面測量參數的變化情況，隨著時間的推移，監測分析發動機性能衰退變化情況。

根據某型發動機所測參數的工程現實，測量參數取為4個，分別為低壓轉子轉速NL、高壓轉子轉速NH、高壓壓氣機壓力P3、尾噴口溫度8T。4個測量參數組成向量其中，i∈{1,…,p}是發動機序號，j∈{1,…,l}是時間序列序號。性能參數初步選取 8個，分別為低壓壓氣機流量變化量ΔMαf、低壓壓氣機效率變化量Δηαf、高壓壓氣機流量變化量 ΔMαc、高壓壓氣機效率變化量Δηαc、高壓渦輪流量變化量ΔMtH、高壓渦輪效率變化量ΔηtH、低壓渦輪流量變化量ΔMtL、低壓渦輪效率變化量ΔηtL。8個性能參數組成向量本文計算數據均采用相對變化量。

全文設計求取性能參數變化量技術路線如圖1所示。

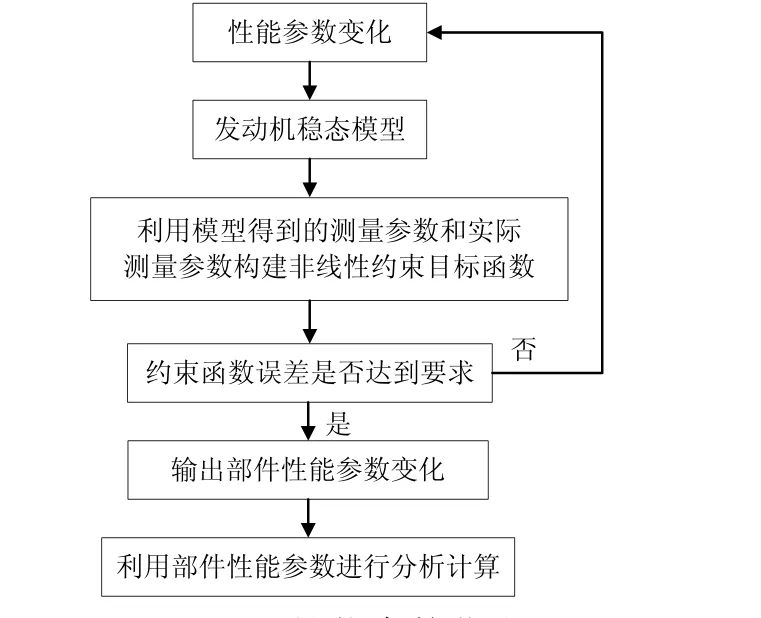
圖1 性能參數獲取

實際中的測量參數容易受到環境等因素的影響，可能攜帶大量的誤差，因此帶入模型計算時首先要經過濾波處理[2]。

如果對8個發動機部件性能參數全部計算，其計算量很大或者根本無解，而根據實際需要，我們也沒有必要計算全部8個參數，因為其中某些性能量變化可能對可測參數的影響非常小。因此，進一步分析，從8個部件性能參數中，優化選取起主要作用的性能參數[3]。

1.2 性能參數的優化選取

從定性的方面分析，發動機性能退化主要反映在推力的減少和耗油率的增加上。在尾噴口幾何面積不變時，推力的減少主要是通過尾噴管的氣流量減少，而燃油流量僅占空氣流量很小的比例，因而推力的減少主要是由于空氣流量減少引起的，故需要考慮低壓壓氣機流量變化量ΔMaf、低壓渦輪流量變化量ΔMtL和高壓渦輪流量變化量ΔMtH。耗油率的增加反映轉子部件效率的降低，由于渦輪處于高溫高壓條件下工作，葉片容易變形，使渦輪效率降低。因此，還需要考慮高壓渦輪效率變化量 tHηΔ和低壓渦輪效率變化量 tLηΔ[4-5]。

通過研究性能參數與輸出參數之間的相關性，做出定量分析，找出性能參數對輸出量影響程度最大的幾個。這里定義相關系數為：

其物理意義是當第m個性能參數變化時，對第n個輸出參數的影響程度。進行相關性分析前，先求出相關系數。采用擾動法，分別改變各性能參數1.0%，計算輸出量相應變化百分數，當h=0，Ma=0時，擾動性能參數后，輸出參數的變化量，見表1。

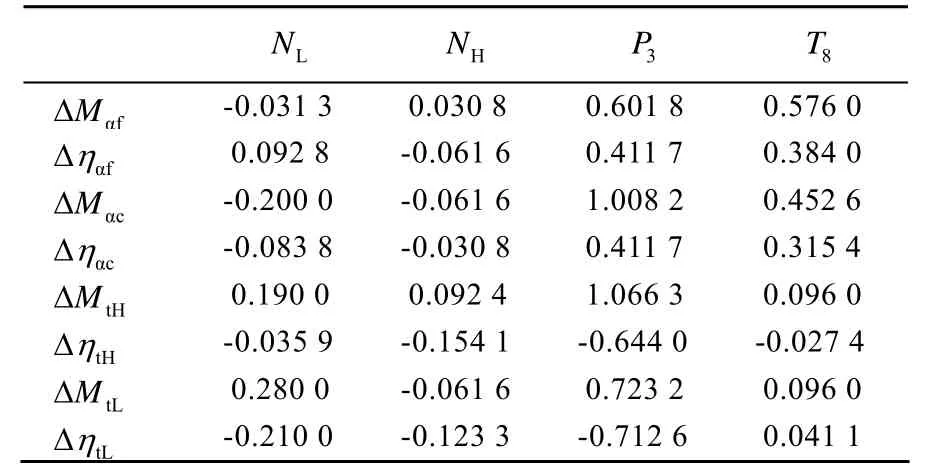
表1 輸出參數變化量

從表1中可以看出，發動機測量參數對不同部件性能參數的改變有不同的變化，其敏感程度同樣因不同的部件性能參數有顯著的不同。為便于分析，找到對某一個輸出參數影響最大的性能參數，應對相關系數進行歸一化處理，按列歸一化原則，按進行歸一化，得到歸一化參數為：

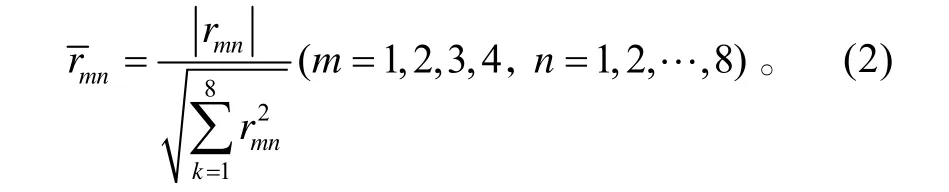
表2是經歸一化后的相關系數表，相關系數大于0.5可以認為是強相關，相關系數在0.3～0.5之間為中等相關，相關系數小于0.3為弱相關。對單個部件性能參數變化引起的各測量參數變化率求和，并進行歸一化處理，得到如圖2所示的測量參數對部件性能參數的敏感圖。

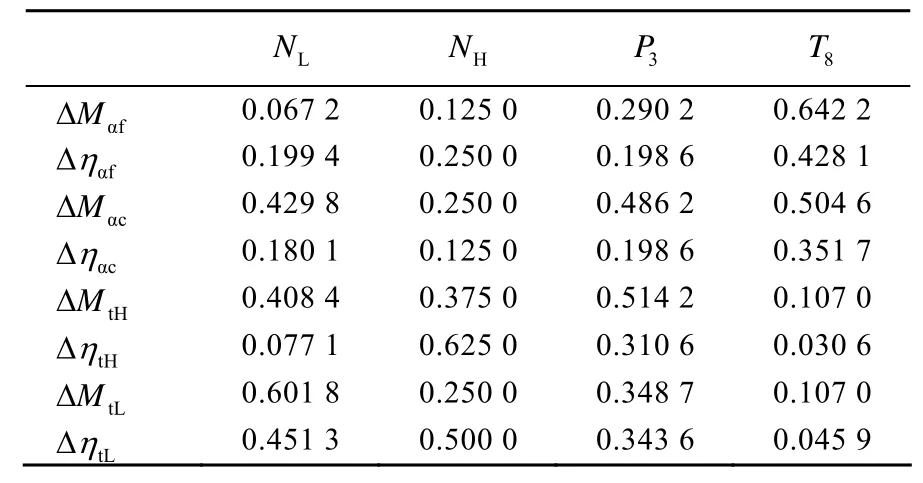
表2 歸一化相關系數

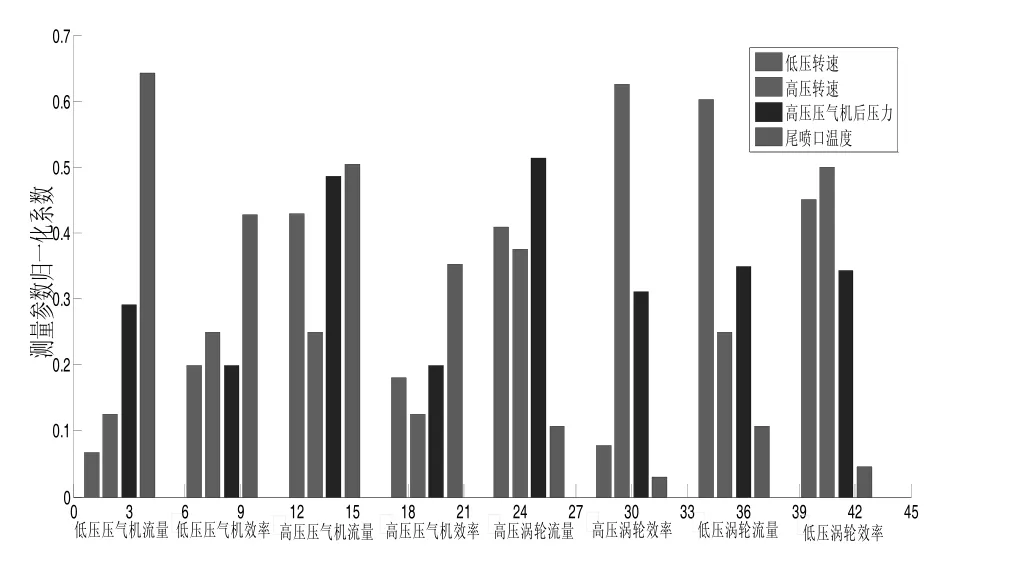
圖2 歸一化的測量參數對部件性能參數的敏感度

從表2和圖2并結合前面的定性分析，本文最終選擇的特性參數為：低壓壓氣機流量變化量ΔMaf、低壓渦輪流量變化量ΔMtL、高壓渦輪流量變化量ΔMtH和高壓渦輪效率變化量 ΔηtH。在實際計算中，保留這些參數用于計算，其余舍去，達到了優化參數的目的。此時，選取的測量參數與性能參數個數相等，按照圖1的計算流程，則性能參數出現唯一解。

2 性能參數殘差時間序列模型的建立

考慮兩種類型的性能參數變化現象(性能參數緩慢變化和突變)，文中采用通過殘差對比的方法判斷性能參數的突變。

采用如下的設計方法，構建性能參數的多元線性回歸模型[6-7]，模型如下：

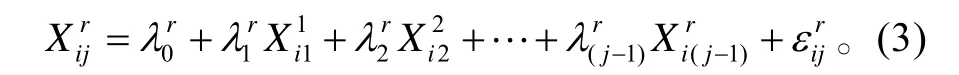
式(3)中：i表示發動機的序號；j表示時間序列序號；X表示發動機性能參數變化；λ表示性能參數的回歸因子；ε為擬合后的殘差。

利用回歸最小二乘法得到發動機性能參數平穩變化部分，與實際值的殘差反映性能參數變化趨勢，突變后的狀況反映性能出現大幅度下降，可能預示著故障的發生，具體算法步驟[8]如下。

1)利用回歸最小二乘法擬合性能參數的線性部分[9]。在每一個時間序列點l，對每一臺發動機i和每一個標準化的發動機性能參數r，線性模型的參數由下述約束得到：

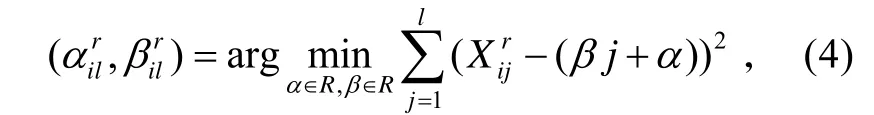
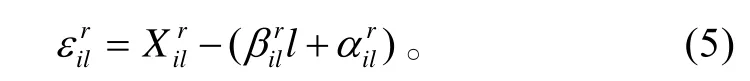
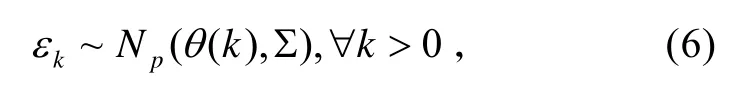
并且

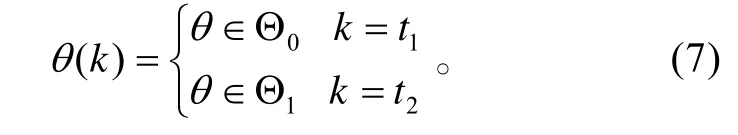
式(7)中：t1、t2是未知時間；Θ0、Θ1是兩個空間不重疊的子集；兩個超球中心都為θ0。

文中取 θ0=[0,0,0,0][11]，Θ0、Θ1如圖3所示。

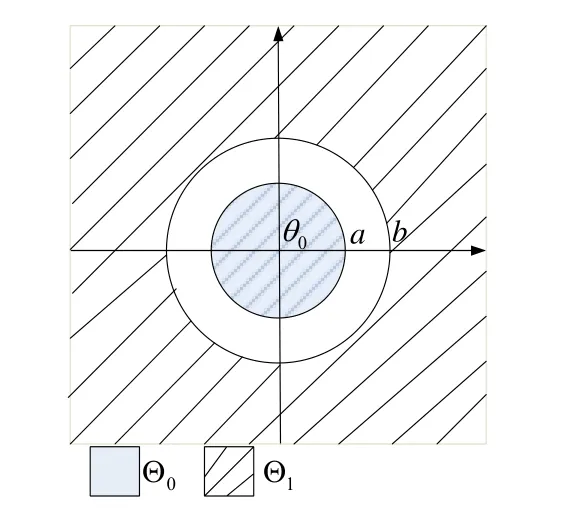
圖3 Θ0、Θ1的空間范圍

Θ0、Θ1范圍定義如下：

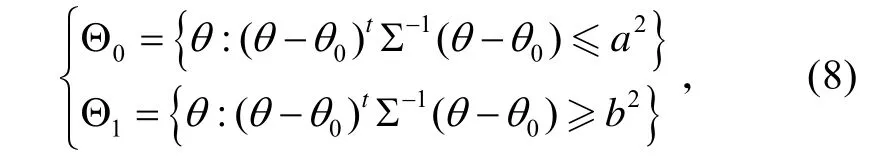
并且，a≤b。

確定性能參數衰退突變點采用的方法：設定時間點αt，表征統計值gk超過特定閾值h的時刻。統計量表示如下：

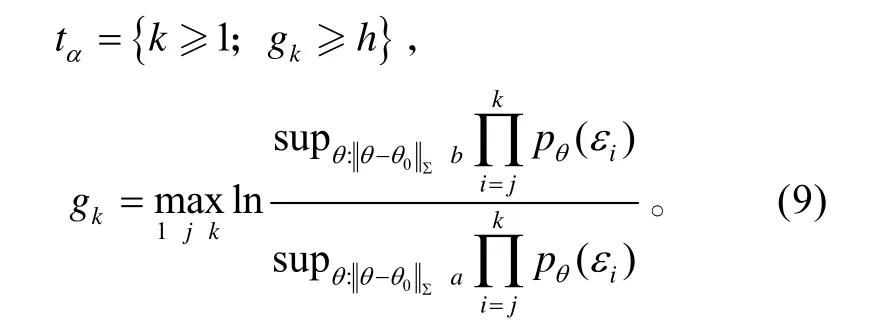
式(9)中：pθ(?)表示均值為θ；方差為Σ 多元高斯分布的密度。此時，Skj表示為：

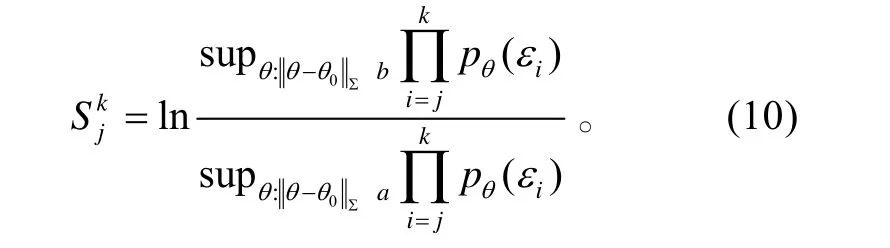
在服從高斯分布情況下，最大值問題式(9)有解析解。此時，Skj表示為：

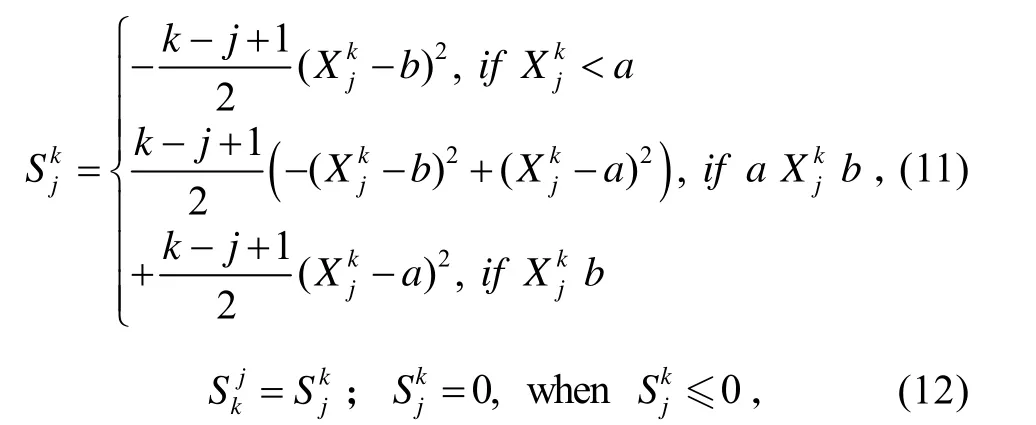
3 仿真分析

選取發動機在最大運用狀態下隨著日歷時間歷程的4個測量參數代入發動機模型進行計算，輸出部件性能參數變化，最后得到性能參數殘差序列，選取其中的某兩段進行分析。

3.1 緩慢衰退過程分析

圖4是性能參數緩慢衰退的殘差示意圖，其中橫坐標n為性能參數的時間序列點，縱坐標為選取的4個性能參數殘差，圖5是由上節算法得到的性能參數緩慢變化對應的突變時刻，當Z坐標出現大于0的點時，判斷性能出現突變；從圖5中可看出，對于性能參數緩慢衰退過程來講，不存在突變點。

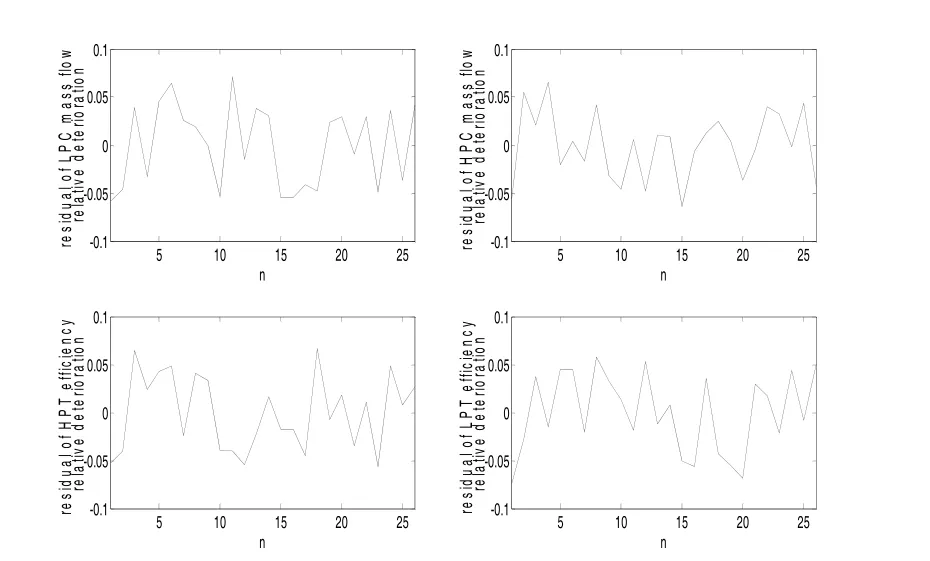
圖4 性能參數緩慢衰退殘差

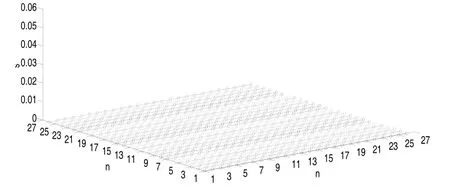
圖5 性能參數緩慢衰退對應的突變時刻

3.2 性能突變時刻的確定

如圖6、圖7所示。

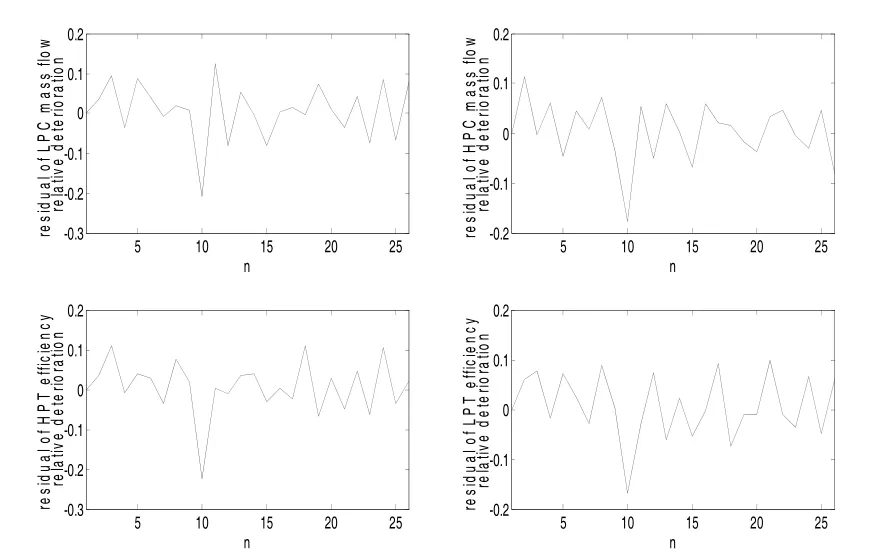
圖6 性能參數殘差變化的時間序列

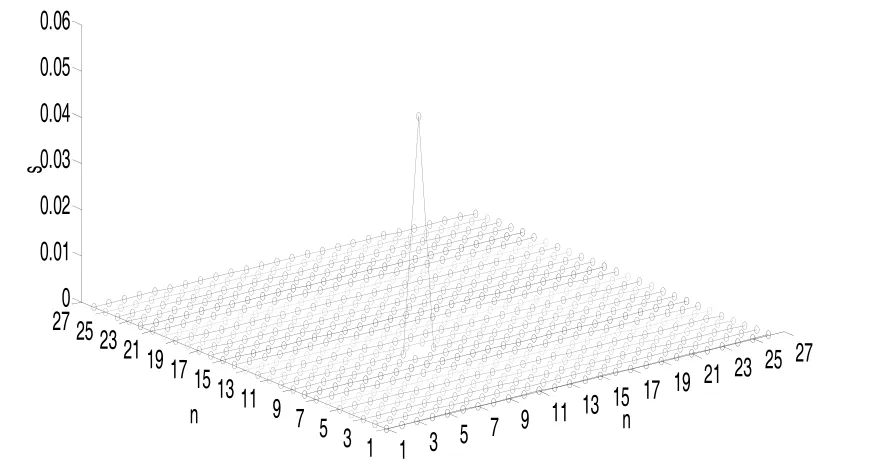
圖7 性能參數殘差變化對應的突變時刻

圖6是性能參數殘差隨時間變化的示意圖。可以看出，4個性能參數殘差在接近時刻10時，殘差開始出現下降，預示性能參數開始出現突變。當到達時刻點10時，4個性能參數殘差絕對值達到最大；另一方面，利用上節確定性能突變時間點的算法后，準確的定位了性能參數發生突變的時刻，見圖7。

4 結論

本文利用發動機模型進行發動機測量參數對部件性能參數的敏感度分析，優化選取充分表征發動機性能衰退的部件性能參數。通過構造性能參數殘差序列，分析性能參數殘差隨時間的變化規律，對發動機性能衰退進行研究。通過對殘差序列的統計量分析，確定性能衰退突變時刻。當性能參數殘差達到最大時，發動機性能會發生突變。經過仿真算例分析驗證了所建模型和所用算法的有效性，為發動機的維護起到了一定的指導作用。

[1]廉筱純,吳虎.航空發動機原理[M].西安∶西北工業大學出版社,2001∶101-104.

[2]李本威,尹大偉,王永華,等.某型渦扇發動機狀態模型修正[J].海軍航空工程學院學報,2008,23(2)∶214-216.

[3]尹大偉.某型發動機模型修正研究[D].煙臺∶海軍航空工程學院,2007.

[4]程禮,李全通.航空發動機狀態監控與故障診斷[M].西安∶空軍工程學院,1997∶31-34.

[5]李建國,李本威.航空發動機故障診斷方程的求解及應用[J].燃氣渦輪試驗與研究,2002,15(2)∶8-11.

[6]馬逢時,何良材,于明書,等.應用概率統計[M].高等教育出版社,1989∶230-241.

[7]司守奎.數學建模算法與程序[M].煙臺∶海軍航空工程學院,2007∶144-157.

[8]徐文彬,齊勇,侯迪,等.基于時間序列分析的應用服務器性能衰退模型[J].西安交通大學學報,2007,41(4)∶427-429.

[9]ETIENNE C?ME,MARIE COTTRELL,MICHEL VERLEYSEN,et al.Aircraft engine health monitoring using self-organizing maps[C]//Proceedings of the Industrial Conference on Data-Mining.Springer,2011∶1-10.

[10]MARIE COTTRELL,PATRICE GAUBERT,CéDRIC ELOY,et al.Fault prediction in aircraft engines using self-organizing maps[C]//Proceedings of the Industrial Conference on Data-Mining.Springer,2009∶37-44.

[11]BASSEVILLE M,NIKIFOROV I.Detection of Abrupt Changes∶Theory and Application[M].1993∶12-24.