面向單機相依任務調度的GPU并行蟻群算法

鄧向陽，張立民，劉 凱，黃曉冬

（海軍航空工程學院 a．電子信息工程系；b．科研部，山東 煙臺 264001）

當前許多系統面臨的都是多機多任務的復雜環境，在一個系統內會不斷出現需要服務的任務，并且在系統中往往存在多個可以進行服務的機器設備，對這類系統執行效率的研究受到了高度重視。此類系統的優化目的一般都是以執行時間最小為目的，是一個調度排序問題。雖然現實中的多機系統很復雜，但是大量多機系統具有松散耦合的特性，不同機器之間任務的聯系不是非常緊密，不同機器之間的資源關聯很小，在這種多機系統的任務調度過程中，可采用單機系統模型的線性疊加實現。另外，單機系統本身也以實體形式存在于許多應用領域。因此，有許多學者對單機調度問題進行了研究，如楊善林[1]等提出了一種啟發式算法，研究了部分可續型單機的最大完工時間調度問題；盧冰原[2]等采用粒子群算法研究了時間參數模糊化的多目標差異作業單機批調度問題模型；王栓獅[3]等采用蟻群算法對一種差異工件單機批調度問題進行了研究。

本文以單機相依任務調度問題(Dependent Task Scheduling on Single Machine，DTSSM)研究為重點，建立單機調度問題的優化模型，基于通用計算架構(Compute Unified Device Architecture，CUDA)在流多處理器(Stream Multi-Processors，SM)中實現基于局部信息素更新的實時種群進化機制，并通過多SM 上基于全局信息素更新機制的多種群協同規約，建立一種基于GPU 的并行蟻群算法，并將該算法結合單機調度問題模型，實現了一種低傳輸量、魯棒性好、并行化計算的單機相依任務調度算法。

1 單機相依任務調度問題模型

單機調度模型是應用領域的一個基本問題，對其進行深入研究是研究復雜多機系統的基礎。單機調度模型主要討論多個任務在單個機器上的執行過程，以達到效益最大化。

每個需要在機器上執行的任務叫做一個單任務，其具有如下性質：

1)由某個機器一次性單獨完成；

2)單任務需求之間可能相互依賴，單任務在不同執行序下所需的時間不同。

據此，DTSSM 問題是一個相依多任務的排序問題，通過建立任務的作業順序，使得任務之間的相依性最大，完成時間最短。DTSSM 問題的數學模型可定義為P=＜ID,T,C＞，其中，P為單任務集合，ID為該任務的編碼集合，T為相依時間關系，C為任務執行的順序號。

設有n個任務{ei}，相依時間關系矩陣為T={tij}，tij表示ej在ei之后執行時需要的時間，要求ej和ei之間具有緊前緊后執行關系，執行序變量為vi,x，其表示ei在第x序號執行，得到的DTSSM問題模型為：

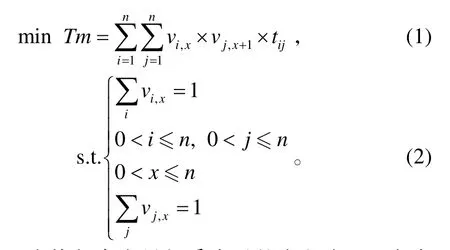
式(1)中2 個執行序變量相乘表示的含義為：只有當ei和ej具有緊前緊后執行關系時，ej的執行時間才計入總時間消耗。

相依時間矩陣T表示了不同任務相依關系下執行時間的經驗，則T為一個非對稱的非負矩陣，通過該矩陣定義了一個非對稱加權的有向圖G=(V,E)，其中頂點為任務ei的集合，弧為相依任務執行時間的集合。如果兩節點代表的任務之間可以相繼執行，則建立弧，權值大小代表了相依執行序下的完成時間，如果2 個任務間不能夠相繼執行，則節點之間不存在弧，而節點的自連接，為任務無緊前任務時的執行時間。

通過上述轉換，相依任務單機調度問題轉為在每個G中搜索一條路徑，該路徑遍歷G的所有節點，使加權和最小。該問題可等效為一個 ATSP (Asymmetric traveling salesman problem)。

2 單機相依任務調度蟻群算法

蟻群算法(Ant Colony Optimization，ACO)是一種群智能算法，通過螞蟻個體之間的簡單行為涌現出復雜的計算能力，具有并行化、正反饋、自組織、容易實現等優點，在不同領域得到了廣泛的應用，ATSP 模型求解是蟻群算法的經典應用領域。本文研究的面向DTSSM 問題的蟻群算法模型以蟻群系統(Ant Colony System，ACS)[4]為基礎，針對單機相依任務調度問題進行設計，定義為單機相依任務調度蟻群算法(DTSSM based on ACO，DTSSM-ACO)。

DTSSM-ACO 算法通過偽隨機比例規則選擇相繼執行任務，根據各條執行路徑上的信息量和啟發函數值來計算狀態轉移概率。設表示螞蟻k在執行完ei后繼續執行ej的概率，可以通過下式計算：

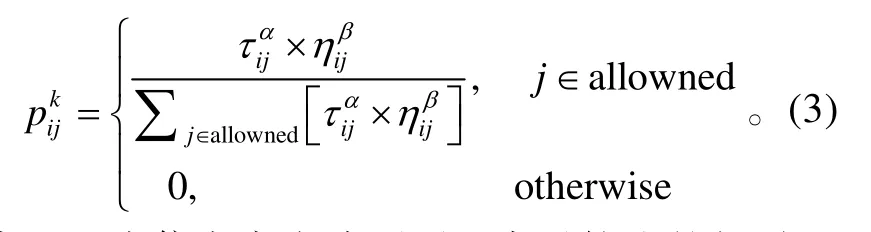
式(3)中：α為信息啟發式因子，表示軌跡的相對重要性；β為期望啟發式因子，表示相依時間關系的相對重要性；τij為弧上的信息素密度；ηij為弧上的啟發函數的值。ηij可以通過下式計算：

式中，tij表示pj在pi之后執行時的所需作業時間。

在每次迭代之后，全局信息素更新通過計算最優路徑上的耗費時間得出，按照如下規則更新最優路徑上的信息素：

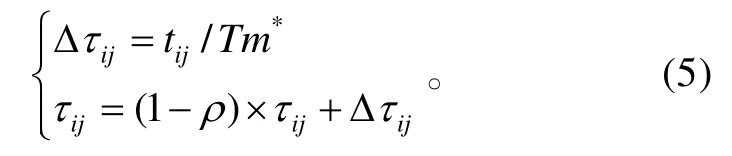
式(5)中：Δτij為路徑上的信息素增量；Tm*為本輪最優路徑所耗費的總時間；ρ為信息素揮發系數。

3 基于GPU的DTSSM-ACO算法并行化設計

3.1 蟻群算法的并行化設計

蟻群算法是一種自然的并行化算法，只有運行在并行環境中才能體現其效能。目前，已有學者針對蟻群算法研究了4 種層次上的并行化：種群層次的并行化、螞蟻層次的并行化、數據層次的并行化和函數層次的并行化[5]。對于種群層次的并行化和數據層次的并行化屬于粗粒度并行化，而螞蟻層次的并行化和函數層次的并行化屬于細粒度并行化。整體來說，對蟻群算法進行并行化研究的文獻較少，主要有M Dorigo[6]等實現了一種多種群的并行蟻群算法，得到了數據層次上的并行化設計；Marcus Randall[7]等設計了一種不需要通信的獨立多處理器并行蟻群算法；于濱[8]等在多處理機上實現了一種粗粒度的并行蟻群算法。

因為一般的并行化需要多個處理器執行，多處理器的調度、并行編程等本身也是一個問題，廣泛應用受到限制。因為GPU 的普及和結構簡單等特點，近幾年有學者將蟻群算法移植到GPU 上實現：李建明[9]等人首次采用GPU 實現了一種細粒度的并行蟻群算法；趙元[10]等人提出了基于多叉樹并行蟻群算法的區位選址優化方法，并采用GPU 對其實現了并行加速設計；白洪濤[11]等人實現了一種基于共享信息素矩陣的并行蟻群算法，并證明了算法是值收斂和解收斂的。

GPU 就是我們通常所說的顯卡的核心部分，它是一種浮點數處理器，是專為圖形數據這種計算密集型、高度并行化的情況而設計的。因此，面向GPU的設計必須轉化為標準的圖形處理過程，這種移植過程需要專業的圖形專業人員，實現難度大。

3.2 基于CUDA 的DTSSM-ACO 并行優化

為了解決GPU 應用專業受限的問題，NVIDIA公司于2007年推出了面向GPU 通用計算的CUDA架構。CUDA 是一種將CPU 和GPU 協同進行計算的架構，通過運行在CPU 上的程序進行任務的分支、選擇等操作，而采用GPU 完成面向數據的處理操作，在CPU 上串行處理，稱為Host 端的處理；在GPU 上并行處理，稱為Device 端的處理。在Host端的主控函數中，依次調用Kernel 函數進行串行運算，而每一個Kernel 函數都是一段GPU 計算過程，調用時都會將計算轉移到GPU 上執行，執行完之后返回。在Device 端的計算過程中，函數的處理過程被組織成大量的并行線程，進行同步處理。CUDA支持大量的線程并行，并在Device 中動態地創建、調度和執行這些線程。

針對前述的DTSSM-ACO 算法，下面實現一種基于CUDA 的多蟻群并行進化，且各蟻群內螞蟻并行執行的兩級并行策略。首先，將每個蟻群組織為一個Block，所有Block 共用一個路徑矩陣存儲空間，每個Block 中的螞蟻進行某個任務階段的路徑搜索工作，每個Block 具有獨立的信息素存儲空間，通過共享存儲器實現通信；每個Block 對應一個SM，在其中分配多個螞蟻，每個螞蟻對應一個線程，在一個流處理器上執行。

在上述的兩級并行策略中，每個蟻群屬于一個Block，該蟻群的所有螞蟻的私有信息，包括已有解路徑、禁忌表等信息，都存儲在共享存儲器中。獨立蟻群在計算過程中，每次螞蟻的移動都采用局部信息素更新策略更新信息素矩陣，信息素矩陣存儲在共享存儲器中，實現獨立種群的即時信息素共享；在所有獨立蟻群執行完畢之后，將各自的信息素矩陣讀回CPU 內存進行規約，并進行所有種群的信息素更新，該過程采用全局信息素更新策略，使不同獨立種群之間進行通信，達到所有螞蟻協同進化的目的。DTSSM-ACO 算法流程如圖1 所示。

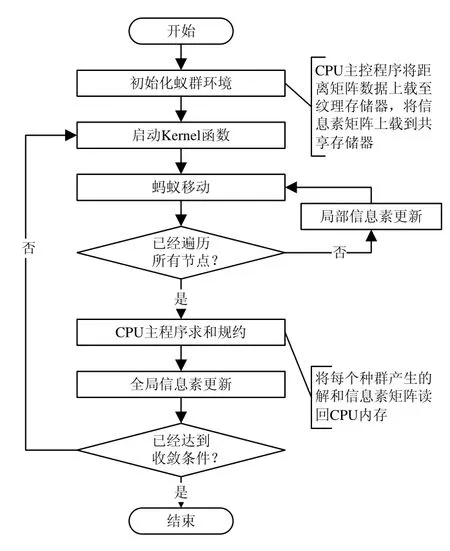
圖1 DTSSM-ACO算法流程

4 實驗結果及分析

DTSSM-ACO 算法實驗的環境為：CPU 為Intel Core i5 760@2.8GHz；內存為4GB RAM；操作系統為Windows 7，顯卡為GeForce GTX 460，CUDA的計算能力為2.1。實驗過程選取了50、100、200、400、800 個任務分5 次測試，任務之間的相依作業時間在[5, 15]之間隨機產生，每個種群輸出30 只螞蟻進行搜索，其他參數設置為ρ=0.1、α=2、β=1.2、τ0=0.001，算法循環300 次，由算法得到的全局最優值曲線和加速比如圖2 所示。

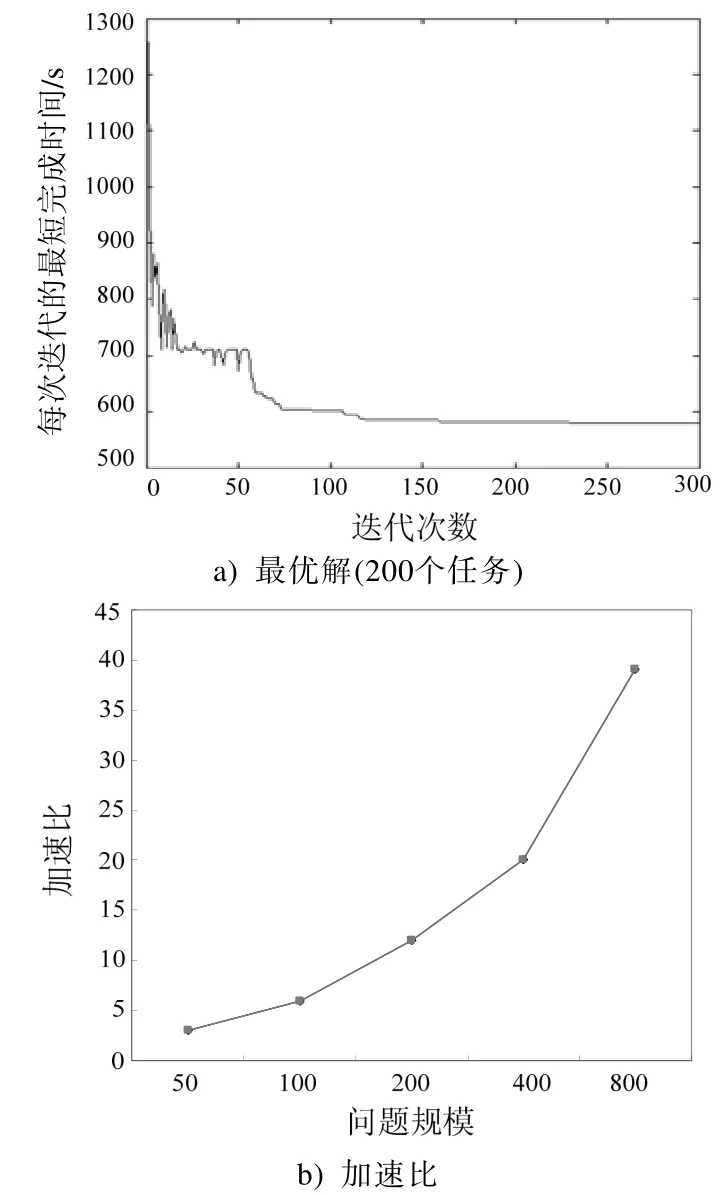
圖2 最優解變化過程和加速比

通過圖2 可分析知，算法在110 次迭代左右達到了收斂狀態，在后期保持了算法的穩定性，表明DTSSM-ACO 算法具有可行性。同時，通過在GPU上的并行優化設計，使得算法在5 種不同規模任務環境中得到了從3 到39 不等的加速比。在任務數較小時，得到的加速比小，這是因為任務數較小時并行算法的大部分時間花在從CPU 內存上載數據到GPU 內存，以及相反的數據傳輸過程，得不到好的加速效果，但是隨著問題規模的增大，大部分時間需要完成計算功能時，加速效果得到了明顯的改善。

5 結論

本文探討了一種單機相依任務調度問題，通過將該問題等效為非對稱TSP 問題，采用蟻群算法對其進行了求解，為了獲得更好的求解效率，對面向單機相依任務調度問題的蟻群算法基于GPU 進行了并行化設計，取得了較好的加速比。但是，本文沒有探討多機環境下的調度模型，也沒有對基于GPU 的并行化算法進行了更加深層次的加速，這將是后續的重點研究內容。

[1] 楊善林, 馬英, 魯付俊. 帶不可用時間段的單機調度問題的啟發式算法[J]. 系統工程學報, 2011,26(4): 500-506.

[2] 盧冰原, 黃傳峰, 賈兆紅. 模糊環境下多目標差異作業單機批調度問題研究[J]. 控制與決策, 2011,26(11): 1675-1680.

[3] 王栓獅, 陳華平, 程八一, 等. 一種差異工件單機批調度問題的蟻群優化算法[J]. 管理科學學報, 2009, 12(6):71-81.

[4] DORIGO M, GAMBARDELLA L M. Ant colony system: a cooperative learning approach to the traveling salesman problem[J].IEEE Transactions on Evolutionary Computation, 1997,1(1):53-66.

[5] ANDRIES P ENGELBRECHT. 計算群體智能基礎[M]. 譚營, 譯. 北京: 清華大學出版社, 2009:303-306.

[6] M DORIGO, DI CARO G. The ant colony optimization meta-heuristic[R]. London: McGraw Hill, 1999.

[7] MARCUS RANDALL, JAMES MONTGOMERY. Candidate set strategies for ant colony optimization[R]. Queensland: School of Information Technology, Bond University, 2002.

[8] 于濱, 程春田, 楊忠振. 一種改進的粗粒度并行蟻群算法[J]. 系統工程與電子技術, 2006,28(4):626-629.

[9] 李建明, 胡祥培, 龐占龍, 等. 一種基于GPU 加速的細粒度并行蟻群算法[J]. 控制與決策, 2009,24(8): 1132-1136.

[10] 趙元, 張新長, 康停軍. 并行蟻群算法及其在區位選址中的應用[J]. 測繪學報, 2010,39(3):322-327.

[11] 白洪濤, 歐陽丹彤, 李熙銘 等. 基于GPU 的共享信息素矩陣多蟻群算法[J]. 吉林大學學報: 工學版, 2011,41(6):1678-1683.