大型風力機氣動彈性響應計算研究

呂計男，劉子強，趙 玲，冉景洪

（中國航天空氣動力技術研究院，北京 100074）

0 引 言

隨著風力發電事業的蓬勃發展，風力機的功率已經由初期的千瓦級小型風力機上升為現在的兆瓦級大型風力機，風力機葉片長度和重量都呈現快速增加的趨勢。風力機葉片的氣動彈性分析需要氣動力載荷及結構數據。目前，氣動力載荷計算主要以動量葉素理論（BEM）及計算空氣動力學（CFD）方法為主。BEM方法簡單快捷，應用方便，理論成熟度高，一直是國內外風力機氣動載荷及氣動彈性問題研究的重要手段。CFD方法可以提供精確的流場描述，但對計算機硬件的要求很高，計算效率較低，特別是對氣動彈性分析所需的非定常氣動力計算尚存在很大難度。

本文選用南京航空航天大學設計的NH1500風輪葉片作為研究對象。該葉片長度40.5m，三維構型由南航優化后NH02系列翼型疊加組成。針對大型風力機葉片氣動彈性響應計算，本課題組開發了一套基于BEM方法的氣動彈性分析程序，該程序可以考慮偏航工況、計及葉尖及輪轂損失、考慮翼型厚度和寬度、風剪切的影響，并可以進行失速修正。本文針對NH1500葉片，比較了本程序計算的氣動載荷結果與商用軟件GH Bladed的結果，驗證了程序可靠性，并給出風力機整機結構在氣動載荷作用下的響應結果。

1 葉片動量葉素理論氣動力建模

1.1 理論基礎

動量理論［1］主要用來估算風力機的理想輸出功率，該理論描述的是風力機葉輪整體與空氣氣流的能量交換情況。葉素理論［1］將風力機葉片簡化為有限個葉素疊加的形式，葉片三維氣動特性由葉素的氣動性能沿徑向積分得到，該理論以葉素表面氣體流動的狀態分析葉片的受力和能量交換。考慮到采用動量理論與葉素理論描述的葉片氣動力與力矩在物理本質上的同一性，可以建立平衡方程得出動量葉素理論中軸向及切向速度誘導因子的顯式表達式［2］。

在理論的基礎上，可以通過葉尖損失系數、輪轂損失系數考慮由于葉尖及根部氣流沿葉片產生的二次流動而引起的力矩的減小［1，3］。

葉柵理論（Cascade Theory）研究葉片厚度和寬度的影響導致的葉素攻角的改變［1］。當周向速度誘導因子大于0.5時，風輪工作在湍流尾流狀態，這時需要對動量理論進行修正。本文的計算模型采用的是 Glauert提出的修正表達式［4－5］：

1.2 風力機坐標系統建模

根據動量葉素理論得到的風力機葉片所受的氣動力與力矩是相當于葉素局部坐標系統的。由于風力機氣動性能最優設計的要求，一般情況下，風輪轉軸傾角，槳葉錐角不為零，這樣使得氣動力／力矩需要完成從葉素局部坐標到全局坐標的坐標變換。此外，葉片旋轉過程中，工作方位角對坐標系統轉換關系的影響也需要考慮。文獻［2］中對該部分內容進行了詳盡的討論。

大型風力機的葉片很長，槳葉不同位置的風速相差很大，一般情況下需要考慮風剪切的影響。本文采用的是指數模型［4，6］：

其中，H代表葉素高度；HR為參考高度；UR為參考高度處的風速；ε為經驗風剪切指數，本文計算模型取值為0.1667。

1.3 計算流程

利用動量葉素理論獲得葉片氣動力主要分為速度誘導因子迭代求解及葉片氣動性能計算兩部分內容，文獻［7］中詳盡了敘述了速度誘導因子迭代的求解過程，這里由于篇幅限制，不再累述。程序的總流程如圖1所示。

圖1 風力機結構響應求解流程圖Fig.1 Structure response solution scheme

1.4 風力機葉片氣動力模型結果分析

南京航空航天大學針對NH1500葉片采用GH Bladed軟件進行了葉片氣動性能的校核。NH1500葉片為南航自主設計，長度40.5m，截面翼型沿葉片展向分別為 NH02＿40、NH02＿35、NH02＿30、NH02＿25、NH02＿21、NH02＿18、NH02＿15，翼型形狀及氣動性能數據為南航提供。針對該葉片，通過編寫程序，完成了葉片氣動力的建模工作，對比結果顯示自編程序的計算結果與南航提供的采用GH Bladed軟件計算的結果吻合的很好，驗證了自編程序的正確性，計算結果如圖2所示。

圖2 功率系數計算結果對比圖Fig.2 Power coefficient contrast

圖2中縱坐標表示功率系數，橫坐標表示來流風速。CpCAAA為本課題組自編程序得到的功率系數數據，CpNH為南航采用GH Bladed軟件計算得到的功率系數數據。

2 風力機全機有限元建模

2.1 葉片結構有限元建模

風力機整體結構在氣動力作用下的響應問題是風力機氣動彈性研究的一個重要方向。結構設計需要根據響應結果獲得彎矩載荷等重要數據。

風力機葉片外形沿葉片展向變化且內部結構復雜，進行結構三維有限元建模難度很大，使得分布氣動力作用下的結構響應計算的代價極大。對響應問題，局部變形對整體響應結果的影響通常不予考慮。借鑒航空氣動彈性問題的做法，將大展弦比機翼結構簡化為梁模型處理，這里將大型風力機葉片也做簡化處理。利用南航提供的結構剛度及質量分布數據通過模態分析可以獲得葉片的結構動力學特性。葉片簡單梁模型與三維有限元模型的結構動力學特性對比如表1所示。

對比結果顯示，除了第四階固有振動的頻率誤差略大之外，其它各階頻率誤差都在有限元模型建模允許誤差范圍之內。

2.2 塔架結構有限元建模

進行風力機全機的響應計算，柔性塔架的影響需要考慮。目前，南航設計的大型風力機只提供了葉片的結構屬性，無塔架屬性可供參考。本部分內容主要根據塔架剛度設計準則［8］，對塔架構成部件及邊界條件進行簡化，建立了塔架的有限元模型。

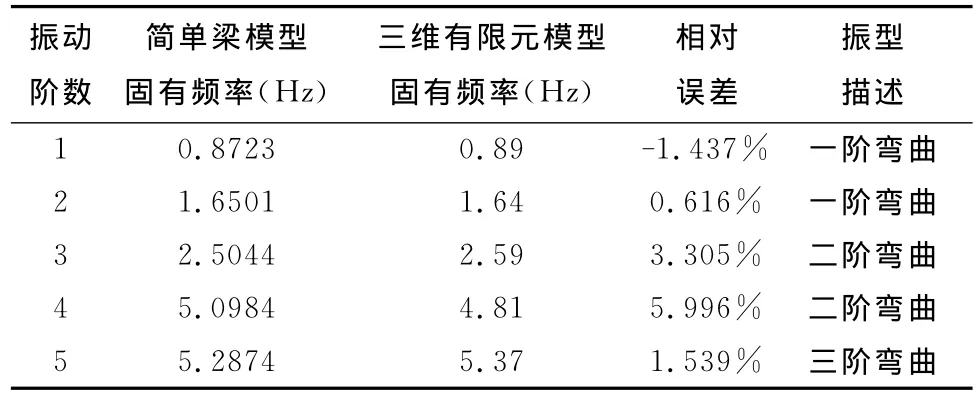
表1 葉片簡單梁模型與三維有限元模型的結構動力學特性對比圖Table1 Structural dynamic characteristic of beam and 3DFE model

塔架結構主要包括塔體及塔頂集中質量。根據剛度設計準則，塔架結構的一階固有頻率以及其上10%，和三階固有頻率以及其下10%，需要避開風力機工作頻率的1倍頻和3倍頻。南航設計的風力機額定轉速17.2RPM／min，即工作頻率為0.287Hz，三倍頻為0.861Hz。根據剛度設計準則，塔架固有振動頻率需要避開的頻率范圍為：0.287Hz～0.316Hz，0.775Hz～0.861Hz。

本文關于塔架的有限元建模沒有考慮法蘭上的螺栓、塔架內部的附屬結構等構件；在塔架頂端創建一個質量單元節點，模擬塔頂質量，質量點的位置設置在機艙、輪轂和葉片的合重心位置處；此外，塔架基礎按固支邊界條件處理。

按照以上條件，塔架的結構動力學特性如表2所示。

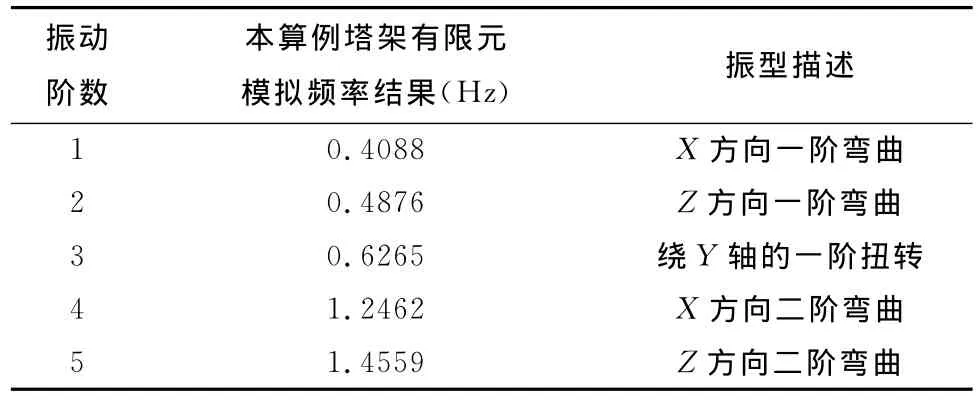
表2 塔架的結構動力學特性Table2 Structural dynamic characteristic of tower

2.3 風力機全機建模

通過商用有限元軟件建立風力機全機模型，葉片結構采用梁單元模擬，塔頂質量采用點質量單元模擬。葉片工作方位角每轉過10°動量葉素氣動力求解模塊求解一次氣動力并保存結果到數據文件。結構分析軟件讀入氣動力數據，氣動載荷以數據表形式施加到結構單元上，含邊界條件的有限元模型如圖3所示。

圖3 風力機全機有限元模型示意圖Fig.3 FE model of total wind turbine

3 計算結果與討論

采用軟件的瞬態動力學分析模塊，結構動力學方程求解采用直接積分法中的Newmark方法，結構阻尼采用Rayleigh阻尼形式。Rayleigh阻尼中的α，β為不依賴于頻率的常數，且阻尼對穩態振動的振幅沒有影響。

考慮柔性塔架作用時，參考高度處來流風速為12m／s時，葉片葉尖節點振動位移隨時間的變化如圖4－圖5所示。由于初始條件設置為零位移、零速度，振動的初始階段會產生跳躍，是強迫振動的過渡階段，隨著時間的進行，振動逐漸進入簡諧激勵下強迫振動的穩態階段。

3.1 揮舞方向振動

葉片X方向及Z（揮舞）方向振動的時程如圖4所示。X方向位移最大值27.27cm，最小值23.91cm，平衡位置為25.59cm，振幅1.68cm。揮舞方向位移最大值20.07cm，最小值17.77cm，平衡位置為18.92cm，振幅1.15cm。

圖4 葉片葉尖X及Z方向振動位移時程圖Fig.4 Response of blade in Xand Zdirection

3.2 擺振方向振動

Y（擺振）方向位移最大值4.51m，最小值4.14m，平衡位置為4.33m，振幅18.85cm，時程如圖5所示。

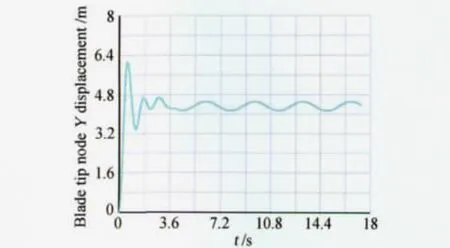
圖5 葉片葉尖Y方向振動位移時程圖Fig.5 Response of blade in Y－direction

3.3 塔架振動

塔架的振動產生結構內部載荷，塔架的振動情況將影響結構的彎矩載荷及疲勞設計。圖6給出塔架頂端節點的時域振動情況。不考慮塔架對葉片的影響，如葉片經過塔架時加速逆風效應時，塔架頂端迎風方向位移最大值7.37cm，最小值6.97cm，平衡位置為7.17cm，振幅0.2cm，時程如圖6所示。

圖6 塔架頂端振動位移時程圖Fig.6 Response of tower in time domain

3.4 幾何非線性

大型風力機葉片長度非常大，受力時會發生大位移小應變的幾何非線性效應，這時平衡方程和幾何關系都是非線性的。早期的非線性有限元分析基本上是線性分析的擴展，只能針對個別具體問題進行分析。近年來基于非線性連續介質力學原理的有限元分析有了很大的發展，商用軟件也有相應成熟的模塊求解該類問題。本部分利用商用有限元軟件分別進行了葉片線性響應分析與幾何非線性響應分析，對比結果如圖7和表3所示。

結果顯示，對葉片葉尖節點，考慮幾何非線性時葉片的變形較小，呈現出比線性分析結果剛硬的性質，這是葉片初位移效應及初應力效應共同作用的結果。

圖7 幾何非線性對葉片振動的影響Fig.7 Influence of geometry nonlinearity

表3 幾何非線性對葉片振動的影響Table3 Influence of geometry nonlinearity

4 結 論

本文建立了一套適用于大型風力機氣動彈性響應的快速計算方法。該方法可以對葉片所受氣動力進行快速預測，并快速的給出結構在氣動力作用下的響應情況，提供了一種可供風力機設計人員借鑒的技術手段。

［1］ROBERT E WILSON，PETER B SLISSAMAN，STEL N WALKER.Aerodynamic performance of wind turbines［M］.Department of Mechanical Engineering，Oregon State University，1976.

［2］劉雄，陳嚴，葉枝全.水平軸風力機氣動性能計算模型［J］.太陽能學報，2005，26（6）：792－800.

［3］PRANDTL L，TIETJENS O G.Applied hydro and aeromechanics［M］.Dover Publications，1957.

［4］DET NORSKE VERITAS and RIS NATIONAL LABORATORY.Guidelines for design of wind turbines［M］.Det Norske Veritas and Ris National Laboratory，2002.

［5］GLAUERT H.The analysis of experimental results in the windmill brake and vortex ring states of an airscrew［R］.Reports and Memoranda，1926.

［6］SPERA D A.Wind turbine technology［M］.New York ASME Press，1994.

［7］ROBERTS E.WILSON，PETER B.S.LISSAMAN.Applied aerodynamics of wind power machines［M］.Or－egon State University Corvallis，1974.

［8］趙立新.風力發電機塔架的有限元分析與優化設計［D］.吉林：吉林大學，2008.