小波熵和BP神經網絡在孤島檢測與擾動辨識中的應用

梁雪飛，陳歆技

(東南大學電氣工程學院，江蘇南京210096)

伴隨著全球范圍內的能源危機，新能源技術受到了世界各國更多的關注。風力發電、光伏發電等分布式電源（DG）接入系統可能引起的孤島現象受到人們越來越多的重視，孤島檢測成為光伏系統并網所必須解決的一個技術問題[1，2]。傳統的孤島檢測技術主要檢測電壓與頻率的波動；與被動檢測法相比，主動檢測法可以在降低檢測盲區的同時，有效地判別孤島的發生，但其向系統中注入的擾動變量對電能質量的影響不可忽視[3]；同時，電力系統中可能存在電壓或頻率波動、諧波或噪聲等污染，這些因素給孤島現象的檢測帶來了一定的困難[4-8]，因此，如何有效區分系統擾動與孤島現象的發生成為孤島檢測檢測技術的關鍵。

小波熵[9，10]以其出色的信號分析與處理能力廣泛地應用于電力系統的故障檢測與診斷中。神經網絡[11，12]作為人工智能算法，其實質反映了輸入轉化為輸出的一種數學表達式，能夠通過對輸入樣本的訓練，提取信號的特征，進而對輸入的檢測信號進行有效分類與辨識。以公共耦合點的電壓作為采樣信號，借助BP神經網絡，通過小波熵值的變化對孤島的發生進行有效檢測，理論與仿真驗證表明，該算法能夠準確識別孤島發生與電壓擾動，從而避免光伏逆變器的誤動作。

1 基于多分辨率分析的小波變換與小波熵

1.1 基于多分辨率分析的小波分解與重構

（1）對長度為N的離散信號采用Mallat算法[13]進行處理，將上一級信號通過高通濾波器Hi_D與低通濾波器Lo_D后，分別得到原信號的細節分量與近似分量，如式（1）所示；隨后對信號的近似分量繼續分解，再次通過高通、低通濾波器，這樣，在選擇了合適的小波基函數與分解層數的基礎上，原信號經過尺度j=1，2，3，…，J（其中J為最大分解尺度）的分解，最終得到D1，D2，D3，…，AJ，其中，D1，D2，D3，…，DJ-1與AJ分別表示信號的高頻細節分量與低頻近似分量。

（2）對分解后的各層系數進行小波變換系數的重構，重構高通、低通濾波器系數分別為與其中與分別是與的對偶算子。

上述即是基于多分辨率分析的小波分解與重構算法。

1.2 小波熵

熵是表征信息的一個普適量[9]，Shannon的信息熵理論指出，對于一個不確定的系統，若用一個取有限值的隨機變量表示其狀態特征，取值為xi的概率pi為：

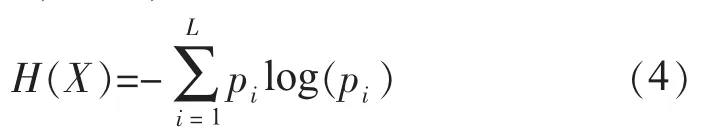
其中，當pi=0時，pilog（pi）=0，信息熵H是在一定的狀態下定位系統的一種信息測度，是對序列未知程度的一種度量，可以用來估計隨機信號的復雜性。

1.3 小波熵的構造

就多尺度小波分解而言，在某一時間窗內，信號的總能量Ppower等于各分量能量之和，進而設因而有于是可定義小波熵WEE為[9]：

2 BP神經網絡

BP神經網絡，即誤差反向傳播算法的學習過程，由信息的正向傳播和誤差的反向傳播2個過程組成。BP神經網絡的出現成功解決了求解非線性連續函數多層前饋神經網絡權重調整問題，廣泛應用于函數逼近、模式識別/分類等領域。

BP神經網絡的節點輸出模型如式（6）和式（7）所示。隱層節點輸出模型為：

輸出層節點輸出模型為：

式中：f為非線性作用函數；q為神經單元閾值。典型BP網絡結構模型如圖1所示。

3 基于小波熵與BP神經網絡的孤島檢測與擾動辨識

考慮到孤島現象的發生往往伴隨著電壓幅值或頻率的變化，因此基于小波熵與BP神經網絡的孤島檢測技術的基本原理是根據光伏電源與本地負載的公共耦合點的采樣電壓在故障前后的變化來判別當前運行狀態。將公共耦合點的采樣電壓經小波分解與系數重構后，計算其各層系數的小波熵值[14，15]，并以此作為BP神經網絡的輸入值，經神經網絡系統處理判別后確定當前電力系統所處的運行狀態，進而控制相應的保護裝置是否將光伏系統切除。

文中采樣電壓信號選自光伏系統與本地負載連接的公共耦合點處，為保證采樣信號的準確性，采樣頻率為6400Hz，即每周波1280 點的采樣速率，經小波變換系數分解與重構后，并根據式（5），分別計算其各層系數的小波熵，此后，將計算出的小波熵值作為神經網絡的輸入，用于判斷當前系統所處運行狀態。文中選擇db6小波對采樣信號進行小波分解與重構；神經網絡采用三層BP網絡，訓練函數選擇tansig函數。根據設計的需要，輸入層為6個輸入單元，輸出層1個輸出單元，而隱層節點個數根據經驗公式（8）[16]選擇為12個。

式中：n為隱層節點個數；ni為輸入節點數；no為輸出節點數；a為1～10之間的任意常數。

文中主要目的在于將電網電壓擾動與孤島現象的出現進行有效辨識，以避免光伏并網逆變器的誤動作。由于要區分的只是兩類情況，而BP神經網絡的輸出值可以限定在（-1，1）范圍內，這樣通過給定相應的訓練數據使得yi=-1表示電網電壓擾動（非孤島），yi=1表示孤島發生。

4 仿真實驗與數據分析

4.1 光伏模型及仿真實驗

通過Matlab/Simulink對4kW單向光伏并網系統進行建模仿真，電網電壓的有效值為220V，負載品質因數以Qf=2.5為例，諧振頻率為50 Hz，如圖2所示。

圖2 單向光伏并網系統

仿真中以斷路器在0.08s斷開模擬孤島現象的發生；為電網電壓施加的擾動時間為0.08～0.14s，持續3個周期共0.06s。

以公共耦合點的電壓作為采樣信號，每周波128個采樣點，采樣頻率為6400Hz，仿真時間為0.2s，共1280 個采樣點。對采樣信號采用db6小波進行6層分解。針對兩類情況4種信號（電壓暫升與暫降、孤島壓降與壓升），分別選取40個樣本作為BP神經網絡的訓練數據，然后選取60個樣本進行測試。

4.2 數據分析

4.2.1 采樣信號的小波熵值

對孤島后電壓升高與降低、電網擾動所致的電壓暫升與暫降4種信號進行小波分解與系數重構，分別選取40組數據作為BP神經網絡訓練數據輸入。4種情況下部分小波熵值如表1所示（以電壓暫升和暫降10%，孤島后電壓升高和降低10%為例）。

表1 兩類信號的小波熵值表

對表1中的小波熵值進行分析，可以看出：同類樣本（孤島后電壓升高與降低、電網擾動所致電壓暫升與暫降）之間小波熵值的變化趨勢非常相似；不同類樣本（孤島與非孤島）之間，小波熵值存在一定不同，但差異不大。由此需要借助BP神經網絡來辨識2類情況下小波熵值的內在特征，從而有效實現區分孤島與非孤島狀態的目的。

4.2.2 算例測試

針對訓練好的BP神經網絡，選取2類信號共60組數據作為測試數據來驗證所提出算法的準確性。測試結果如表2所示（選取其中的12組列表）。

表2 BP神經網絡測試結果

表2中BP神經網絡的測試結果與目標輸出誤差相對較小，可以準確有效地將孤島與擾動區分。

4.2.3 噪聲測試

電力系統測試中不可避免的會受到噪聲的影響，因此在進行孤島與擾動區分時必須將噪聲污染加以考慮。在采樣信號中加入信噪比為20 dB的高斯白噪聲，選取30組測試數據再次進行孤島與擾動的辨識。受篇幅限制，表3只列出其中的8組數據。

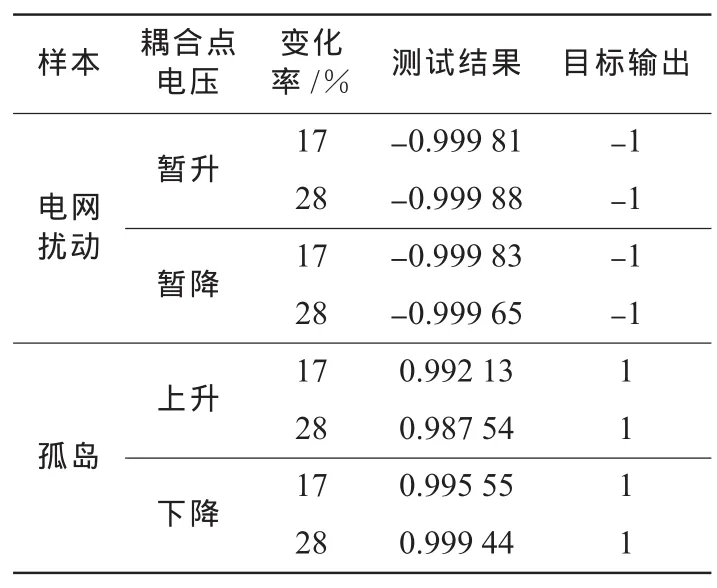
表3 BP神經網絡噪聲測試結果

添加噪聲后，各組信號的各層熵值發生明顯變化，但仍然保持表1所描述的特性，并沒有影響最終的測試結果。因此該算法具有較高的準確性。

5 結束語

文中將小波熵與BP神經網絡結合起來，作為光伏并網系統的一種孤島檢測技術。選取公共耦合點的電壓作為參考輸入，進行小波變換與系數重構后，計算每一層系數的小波熵，以此作為BP神經網絡的訓練輸入。仿真算例表明，該設計方案能夠有效地區分孤島與擾動，進而避免光伏并網逆變器的誤動作。

[1] IEEE Std 929－2000，IEEE Recommended Practice for Utility Interface of Photovoltaic(PV）Systems[S].

[2] 曹海燕，田悅欣.并網逆變器孤島控制技術[J].電力系統保護與控制，2010，38（9）：72-74.

[3] 郭小強，趙清林，鄔偉揚.光伏并網發電系統孤島檢測技術[J].電工技術，2007，22（4）：157-162.

[4] 禹華軍，潘俊民.無功補償技術在光伏并網發電系統孤島檢測中的應用[J].電工電能新技術，2005，24（3）：22-26.

[5] 劉芙蓉，康勇，段善旭，等.主動移頻式孤島檢測方法的參數優化[J].中國電機工程學報，2008，28(1)：95-99.

[6] 李軍，黃學良，陳小虎，等.基于分壓器原理的孤島檢測技術在微電網中的應用[J].中國電機工程學報，2010，30（34）：15-21.

[7] 李春玲.基于光伏并網發電系統的孤島檢測[D].天津：天津大學，2008.

[8] PIGAZO A，LISERRE M，MASTROMAURO R A，et al.Wavelet-based Islanding Detection in Grid-connected PV Systems[J].IEEE Transactions on Industrial Electronics，2009，56(11)：4445-4455.

[9] 何正友，劉志剛，錢清泉.小波熵理論及其在電力系統中應用的可行性探討[J].電網技術，2004，28（21）：17-21.

[10] 劉瑞葉，龍志剛.小波熵及小波變換的短期負荷預報[J].哈爾濱理工大學學報，2007，12(4)：62-65.

[11] 叢爽.面向Matlab工具箱的神經網絡理論與應用[M].合肥：中國科學技術大學出版社，2009.

[12] 侯媛彬，杜京義，汪梅.神經網絡[M].陜西：西安電子科技大學出版社，2007.

[13] 郭晶，孫偉娟.小波分析理論與matlab7實現[M].北京：電子工業出版社，2005.

[14] 朱艷偉，石新春，李鵬.分辨奇異譜熵和支持向量機在孤島與擾動識別中的應用[J].中國電機工程學報，2011，31(7)：64-70.

[15] 何正友，錢清泉.多分辨信息熵的計算及在故障檢測中的應用[J].電力自動化設備，2001，21(5)：9-11.

[16] 周開利，康耀紅.神經網絡模型及其MATLAB仿真程序設計[M].北京：清華大學出版社，2009.