一種新的基于二值水平集和形態學的局部分割方法

鄭 強 董恩清

(山東大學(威海)機電與信息工程學院 威海 264209)

1 引言

圖像分割是圖像處理領域中的熱點問題之一。主動輪廓模型(Active Contour Model, ACM)[1]以其強大的數學理論基礎和基于水平集(level set)的高效數值方案吸引了眾多學者。主動輪廓模型分為兩類：基于邊緣信息的模型[2,3]和基于區域信息的模型[4,5]，這兩類模型的典型代表分別是測地主動輪廓(Geodesic Active Contours, GAC)模型[2]和 CV(Chan-Vese)模型[4]。

在實際應用中，經常只需分割感興趣的特定區域，即局部分割，如醫學實踐中常常需要對具有解剖意義的殼核、小腦等特定組織進行分割。基于邊緣信息的模型雖能實現局部分割，但對噪聲敏感，對邊緣較弱圖像的分割能力較差；基于區域信息的模型雖對噪聲、弱邊緣等問題具有較強的魯棒性，但其模型是一種全局分割模型，會將圖像中具有相近亮度的區域都分割出來，無法實現局部分割。

特別強調的是，本文中局部分割的概念與基于局部統計信息的分割模型是不同的。局部分割(local segmentation)指的是從復雜圖像中分割局部區域，而基于局部統計信息的分割模型(local region-based model)是一種全局分割(global segmentation)模型。兩者之間的相同點是，本文的局部分割模型和基于局部統計信息的分割模型都會用到局部統計信息。

局部分割是一個具有挑戰性的課題，局部分割精度(Local Segmentation Precision, LSP)不足和窄帶控制不穩定是當前局部分割方法中存在的兩個主要問題。近年來，局部分割逐漸引起眾多學者的重視[6-11]，其中 Lankton等人[6]的研究最具代表性。他們提出一種局部分割框架 LRBAC (Localizing Region Based Active Contours)，該框架允許任意基于區域信息的模型以局部的形式表達，將曲線進化過程控制在零水平集附近的窄帶范圍內。實驗結果表明，該框架是一種非常有效的局部分割方法，對灰度不均勻圖像也能取得較好的分割結果。然而，該方法存在以下不足：(1)水平集函數需要不斷重新初始化為符號距離函數作為保證，并且為了保證算法的穩定性，進化步長必須滿足 CFL(Courant-Friedrichs-Lewy)條件，這些將導致該方法的計算量較大；(2)水平集函數重新初始化過程中存在誤差導致窄帶控制方案不穩定。

基于LRBAC方法，Mille[7]提出一種窄帶主動輪廓模型，該模型能夠更好地控制窄帶，并且構建了基于曲率的模型；胡玉暉[8]提出一種基于局部子區域的活動輪廓模型，較好地解決了復雜多紋理圖像中的目標分割問題。然而，兩者都沒有解決LRBAC方法[6]中符號距離函數所帶來的困擾。Zhang等人[9]提出一種可以選擇局部分割或是全局分割的圖像分割方法 SBGFRLS(Selective Binary and Gaussian Filtering Regularized Level Set)方法，該方法用可選擇的二值水平集函數實現局部分割，并且用高斯濾波實現曲線平滑。然而，該方法對灰度不均勻圖像分割能力不足，且局部分割精度受高斯濾波影響較大。

本文在LRBAC方法的基礎上，提出一種新的局部分割方法 BSMORLS(Binary and Selective Morphological Operation Regularized Level Set)。主要思路如下：(1)用二值水平集取代傳統的符號距離函數以降低計算量，并通過嚴格保持水平集函數的二值性以確保窄帶控制的穩定性和局部分割的精度；(2)引入局部統計信息，增強對灰度不均勻圖像的分割能力；(3)用可選擇的形態學算子改進曲線平滑項，增加曲線平滑的靈活性；(4)本文方法用稀疏場算法實現以提高計算效率。在合成圖像和醫學圖像上的實驗結果表明，提出的方法能更好地實現圖像局部分割。

2 局部分割模型(LRBAC)

文獻[6]提出的局部分割框架LRBAC是圖像局部分割模型的典型代表。設圖像I的定義域為Ωx，變量x表示定義域Ωx上的任意一點，即x∈Ωx。C是用符號距離函數的零水平集表示的閉合曲線，即C= {x|φ(x)=0 }。用海維塞德函數(Heaviside Function)指定閉合曲線C的內部部分：

同理，閉合曲線C的外部部分用(1 -H(φ(x)))表示,并用海維塞德函數的導數δ(φ(x))來指定圍繞在進化曲線附近的窄帶區域：

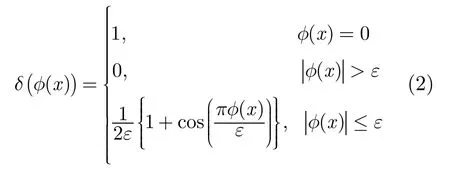
為了引入變量y，定義如下特征函數

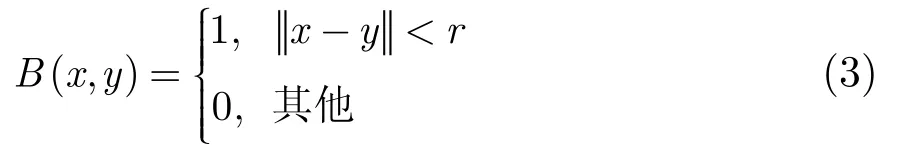
當y在以點x為圓心，r為半徑的圓的內部時，其取值為1，否則為0。Ωy為變量y的定義域，即y∈Ωy。函數B(x,y)用來標記局部鄰域，且被閉合曲線C分為局部內部區域和局部外部區域。

如圖1所示，取δ(φ(x))控制的窄帶區域上任意一點為圓心，r為半徑做圓，則圓被閉合曲線C分為局部內部區域(圖1閉合圓中的“1”標記部分)和局部外部區域(圖1閉合圓的“2”標記部分)。

因此，LRBAC方法的局部分割模型如下：

函數F(I(y),φ(y))為任意基于區域信息的能量模型，文獻[6]分析了 3種能量模型：UM(Uniform Modeling)能量模型，MS(Mean Separation)能量模型和HS(Histogram Separation)能量模型。本文以UM能量模型中的典型代表CV模型為例，式(4)的梯度下降流為

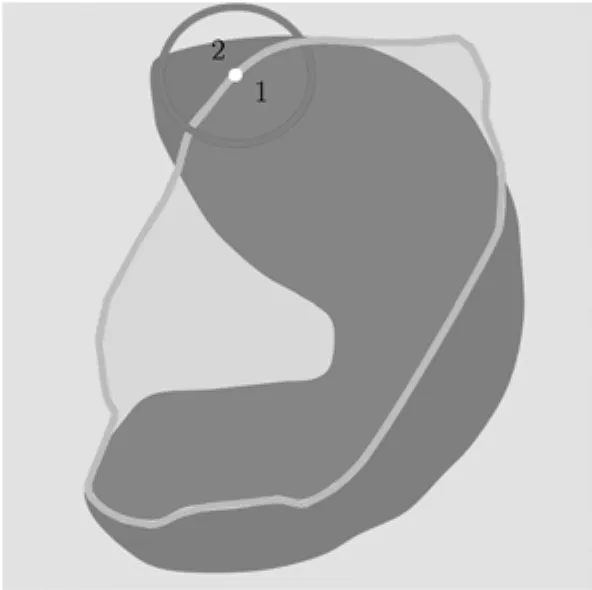
圖1 局部化模型示意圖

3 本文方法及相關問題分析

本文針對局部分割中存在的兩個問題，引入二值水平集函數取代傳統的符號距離函數，并用二值水平集函數的取代式(5)中δ(φ(x))以精確控制圍繞在進化曲線附近的窄帶區域，并且在每次迭代時都嚴格保證水平集函數的二值性。與LRBAC[6]方法相同，本文引入局部統計信息，增加對灰度不均勻圖像的分割能力。同時，本文提出用可選擇的形態學算子(開運算、閉運算和中值集算子)作為新的曲線平滑方案，增加曲線平滑的靈活性。為了提高計算效率，本文方法采用稀疏場算法實現。特別說明的是，二值水平集的用中心差分實現，后文中若無特別說明均以此為準。

另外，Zhao等人[12]也曾將曲線進化公式中的δ(φ(x))用取代，取代的目的是為了擴大曲線進化范圍。因為當進化曲線離圖像邊緣較遠時，δ(φ(x))函數會抑制離進化曲線較遠的圖像邊緣的檢測，而符號距離函數滿足，可以消除δ(φ(x))函數對非零水平集的抑制。這與本文方案是有本質區別的。在本文方案中，二值水平集函數的并沒有改變δ(φ(x))函數窄帶控制的原始思想，采用二值水平集函數的取代δ(φ(x))函數是為了使得窄帶控制更加穩定和精確，從而更加有利于實現圖像局部分割。

3.1 本文方法(BSMORLS)

綜上，本文提出的圖像局部分割方法如下：

(1)初始化水平集函數φ(x)

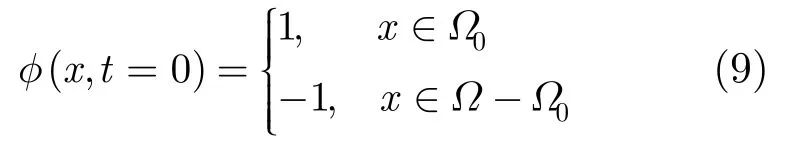
其中Ω0是圖像定義域Ω的一個子集。

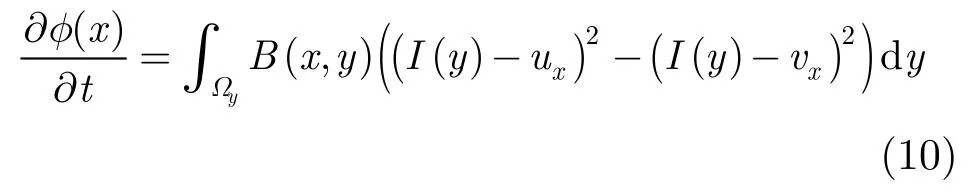
其中ux和vx用式(7)和式(8)更新，用中心差分實現。值得注意的是，式(10)除了將式(5)中的δ(φ(x))函數用函數取代以更加準確而穩定的選取窄帶內的點以外，還將式(5)中的δCV(φ(y))函數去掉。

Chan等人[13]指出，由于CV模型用非緊支撐且光滑的函數逼近海維塞德函數HCV(φ(y))，因此，CV模型的梯度下降流

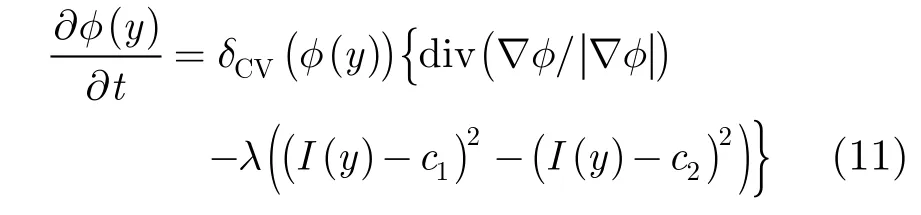
與式(12)具有相同的穩態解

因此，將式(5)中的δCV(φ(y))函數去掉是合理的。

(3)對步驟(2)中更新的窄帶內的點取如下運算

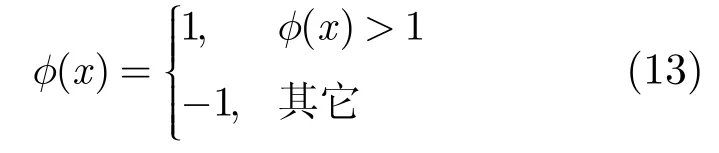
(4)用可選擇的形態學運算平滑曲線，主要包括開運算、閉運算和中值集運算。

用可選擇的形態學運算平滑曲線不但更加有利于保持水平集函數的二值性，并且能夠增加曲線平滑的靈活性，使其更加有利于實現圖像局部分割。

(5)判斷進化曲線是否收斂，若沒有收斂，則轉到步驟(2)，若收斂，則停止曲線進化。

為提高運算速度，本文方法采用稀疏場算法實現。稀疏場算法一般用數據鏈表的形式實現，本文提出用二值水平集函數的作為新的數據鏈表。如圖 2,Lout和Lin是由控制的窄帶的非零數值區域，數據寬度是2ρ。以閉合曲線為分界線，Lout和Lin分別為數據鏈表的外部部分和內部部分。一般假定Lout和Lin的寬度相同，且都為ρ。本文算法在實現過程中只提取控制的窄帶之內的點(Lin和Lout)進行更新，此舉提高了計算效率。

圖2 數據鏈表及局部分割精度示意圖

3.2 相關問題分析

本文主要對局部分割精度、窄帶控制的穩定性、曲線平滑方案等問題進行分析。

(1)局部分割精度及窄帶控制穩定性分析

定義局部分割精度(Local Segmentation Precision, LSP)ρ是曲線法線方向上參與水平集函數進化，且對曲線進化有貢獻的數據寬度。如圖 2所示，參與水平集函數進化的數據寬度是2ρ，但是由于曲線上的點只能沿一個方向進化，即向內或者向外，所以實際對曲線進化有貢獻的數據寬度是ρ。數據寬度越寬，LSP越低；數據寬度越窄，LSP越高。

LSP對局部分割有重要意義。如圖3所示為兩目標由遠及近的情況下的局部分割結果，其中方形閉合曲線為初始輪廓。圖3(a)和圖3(b)都采用較低的LSP；圖3(c)和圖3(d)都采用較高的LSP。實驗結果表明，當兩目標距離較遠時，LSP對局部分割影響較小；當兩目標距離較近時，若LSP較低，則兩目標之間會互相干擾，導致無法實現局部分割，只有當LSP較高時，才能較好的實現局部分割。

圖3 局部分割精度分析

結合以上定義，分析LRBAC方法中的δ(φ(x))函數，SBGFRLS方法中的函數與本文BSMORLS方法的函數發現，三者控制的都是 LSP。δ(φ(x))函數建立在符號距離函數的基礎上，函數建立在二值水平集函數的基礎上。為方便圖示，假定控制 LSP的函數為L(φ(x))，則L(φ(x))可 能 為δ(φ(x)),或。分析圖4發現，δ(φ(x))函數是一平滑鐘形函數(ε=1.5)，而(高斯濾波器大小為3×3)和函數類似于理想的低通濾波器。顯然，只要能夠保持水平集函數的二值性，比δ(φ(x))能更精確更穩定地控制窄帶區域，且比函數的 LSP更高。根據 LSP的定義，若用中心差分實現，則本文方案的LSP可以穩定地控制在一個像素的精度。一個像素寬度是較為理想的LSP，如果LSP小于一個像素寬度則會影響進化速度，而如果LSP大于一個像素寬度，對于圖像中存在相距較近目標的情況下，圖像局部分割結果則有可能出現目標之間互相干擾的現象。

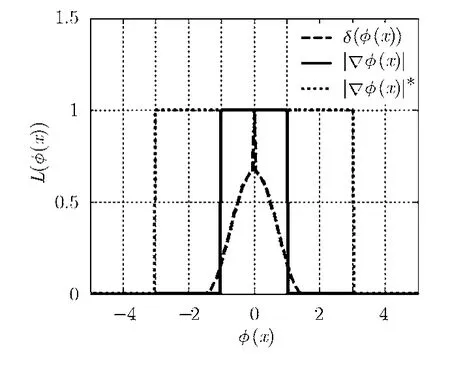
圖4 局部分割精度控制函數

在SBGFRLS方法中，在使用3×3大小的高斯濾波器的情況下，LSP不能達到一個像素的精度。下面特別說明，當使用更小尺寸如2×2大小的高斯濾波器的情況下，LSP也不能穩定地達到一個像素的精度，從而證明不論高斯濾波器的大小如何，SBGFRLS方法中LSP都不能穩定地達到一個像素的精度。設定φ(x)為如下二值水平集，且考慮零水平集處于豎直狀態下的情況，G(x)是大小為2×2方差為1.0的高斯濾波器。

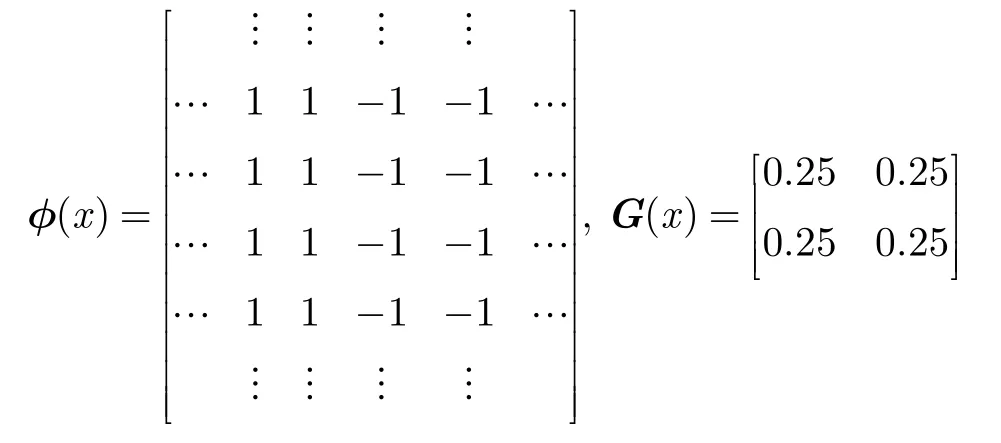
二者卷積后得

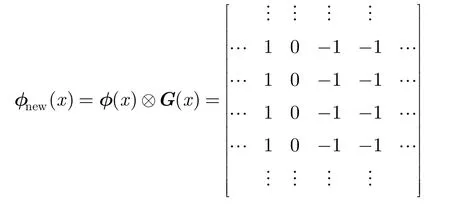
若用中心差分由φnew(x)求得則LSP必大于 1。因此，不論高斯濾波器的大小如何，SBGFRLS方法中LSP都不能穩定地達到一個像素的精度。

(2)曲線平滑方案分析 本文提出用可選擇的形態學算子(開運算、閉運算和中值集運算)作為曲線平滑方案基于以下原因：

(a)形態學運算不但具有較好的平滑作用，而且更容易保持水平集函數的二值性。LRBAC[6]采用曲率作為平滑方案，SBGFRLS[9]采用高斯濾波作為平滑方案，都與形態學中值集運算的平滑效果基本相同，但是形態學算子在運算前后更加容易保持水平集函數的二值性。在本文方法中嚴格保持水平集函數的二值性是一個核心問題。

(b)用可選擇形態學算子作為曲線平滑方案是基于圖像特征的考慮。開運算只磨光凸向圖像外部的邊角，而能夠保留凸向圖像內部的邊角。閉運算只磨光凸向圖像內部的邊角，而能夠保留凸向圖像外部的邊角。對于沒有特別明顯或者特別尖銳邊角的圖像，則可以用中值集運算平滑曲線。這極大增加了曲線平滑方案的靈活性。

圖5所示是曲線平滑方案對比分析圖，其中方形閉合曲線為初始輪廓。圖5(a)和圖5(b)分別用形態學中值集算子和開運算作為平滑方案的分割結果；圖5(c)和圖5(d)分別用形態學中值集算子和閉運算作為平滑方案的分割結果。實驗結果表明，開運算能保留凸向圖像內部的邊角，閉運算能保留凸向圖像外部的邊角，增加曲線平滑方案的靈活性將更加有利于實現圖像局部分割。

4 實驗結果及對比分析

由于 SBGFRL[9]方法基于全局統計信息，對灰度不均勻圖像的分割能力不足，為了增加可比性，本文將該方法的數據驅動力改為與本文相同，在相同數據驅動力的前提下更能證明本文方案在局部分割中的優勢。此處特別標記，原文獻[9]中的方法為SBGFRL(G)，修改數據驅動力后的方法為SBGFRL(L), L和G分別指基于局部的統計信息和基于全局的統計信息。

為了分析和驗證本文提出的局部分割算法BSMORLS的實際效果，試驗中同時采用了LRBAC[6]方法、SBGFRLS(G)[9]方法和 SBGFRLS(L)方法一同對灰度不均勻圖像進行局部分割，其中方形閉合曲線為初始輪廓。

圖6和圖7是對灰度不均勻圖像的分割結果。圖6(a)為LRBAC 方法的分割結果，局部鄰域半徑為15；圖6(b)為SBGFRLS(G)方法的分割結果，高斯濾波器大小為5×5，方差為 1.0；圖 6(c)為SBGFRLS(L)方法的分割結果，局部鄰域半徑為15，高斯濾波器大小為5×5，方差為 1.0；圖 6(d)為本文BSMORLS方法的分割結果，局部鄰域半徑為15，曲線平滑方案選為形態學閉運算。實驗結果表明，LRBAC 方法受窄帶控制不穩定影響，分割過程中出現窄帶范圍之內搜索不到點參與曲線進化，從而迫使曲線進化停止的現象；SBGFRLS(G)和SBGFRLS(L)方法由于LSP不夠，相鄰目標之間會出現互相干擾的現象，此外，對比圖6(b)和圖6(c)發現，SBGFRLS(G)對灰度不均勻圖像的分割能力不足；本文提出的BSMORLS方法由于LSP高，對灰度不均勻圖像的分割能力較強，曲線平滑方案選取靈活，因此能夠達到較好的分割效果。

圖5 曲線平滑方案對比分析

圖6 灰度不均勻圖像分割結果

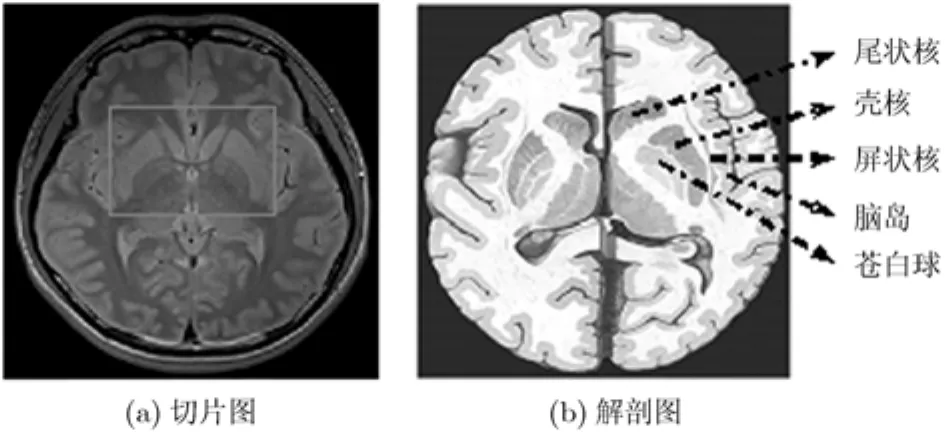
圖7 含有殼核區域的整個腦部切片圖及解剖結構

圖7(a)為取自橫軸位質子和 T2加權快速自旋雙回波序列(TSE-PD/T2)中的含有殼核區域的一張腦部切片圖，磁共振圖像來自于威海市市立醫院；圖7(b)為相應的解剖結構。在MR腦圖像中，殼核的分割受殼核外側的屏狀核及腦島影響較大，因為殼核外側與屏狀核之間僅有一層很薄的外囊相隔，距離非常近，在MR腦圖像中一般只有一到兩個像素的寬度，而腦島和屏狀核之間距離也非常近，所以在分割殼核區域時分割結果常會受到屏狀核甚至腦島區域的干擾，造成誤分割。另外，尾狀核對殼核的分割也有一定的干擾。圖8給出相應實驗結果。

圖8為對幾種算法對殼核區域的分割結果對比圖。圖8(a)為LRBAC 方法的分割結果，局部鄰域半徑為11；圖8(b)為SBGFRLS(G)方法的分割結果，高斯濾波器大小3×3，方差 1.0；圖 8(c)為SBGFRLS(L)方法分割結果，鄰域半徑 11，高斯濾波器大小3×3，方差 1.0；圖 8(d)為本文BSMORLS方法的分割結果，鄰域半徑11，曲線平滑方案用形態學閉運算。實驗結果表明，LRBAC 方法受窄帶不穩定影響，分割過程中出現窄帶范圍之內搜索不到點參與曲線進化，從而迫使曲線進化停止的現象；SBGFRLS(G)和SBGFRLS(L)方法由于LSP不夠，尾狀核、屏狀核和腦島對殼核的分割都存在干擾現象；本文提出的 BSMORLS方法由于LSP高，對灰度不均勻圖像的分割能力較強，曲線平滑方案選取靈活，因此能夠達到較好的分割效果。

此外，在MR腦圖像中，殼核上半部分成像比較清晰，下半部分靠近蒼白球的一側成像也比較清晰，而下半部分靠近屏狀核的區域比較模糊，在分割過程中閉合曲線容易出現凸向外部的邊角，因此分割殼核區域時曲線平滑方案采用形態學閉運算將更加有利于局部分割。圖9給出相應的對比分析。

圖9為不同曲線平滑方案對分割影響對比圖。圖 9(a)-9(d)都用本文方法進行分割，局部鄰域半徑為11，但每個圖所對應的曲線平滑方案不同。圖9(a)為無任何曲線平滑方案時分割結果；圖 9(b)為用形態學中值集運算作為曲線平滑方案時分割結果；圖 9(c)為用形態學開運算作為曲線平滑方案時分割結果；圖9(d)為用形態學閉運算作為曲線平滑方案時分割結果。實驗結果表明，針對殼核區域的分割，選用形態學閉運算更加有利于分割。由此可見，靈活選取曲線平滑方案將更加有利于局部分割。

5 結束語

圖像分割是圖像處理中的研究熱點，當前的分割方法大多熱衷于全局分割，而在實際應用尤其是醫學圖像中卻更多地要求局部分割。局部分割是一個具有挑戰性的課題，窄帶控制不穩定和局部分割精度不足是當前局部分割方法中存在的兩個主要問題。本文提出一種新的局部分割方法，能夠較好地解決以上問題，并且進一步增加了曲線平滑的靈活性，稀疏場運算的引入使得本文方法實現更加簡單。應用合成圖像和醫學圖像對幾種方法進行對比分析，本文方法能更好地實現圖像局部分割。

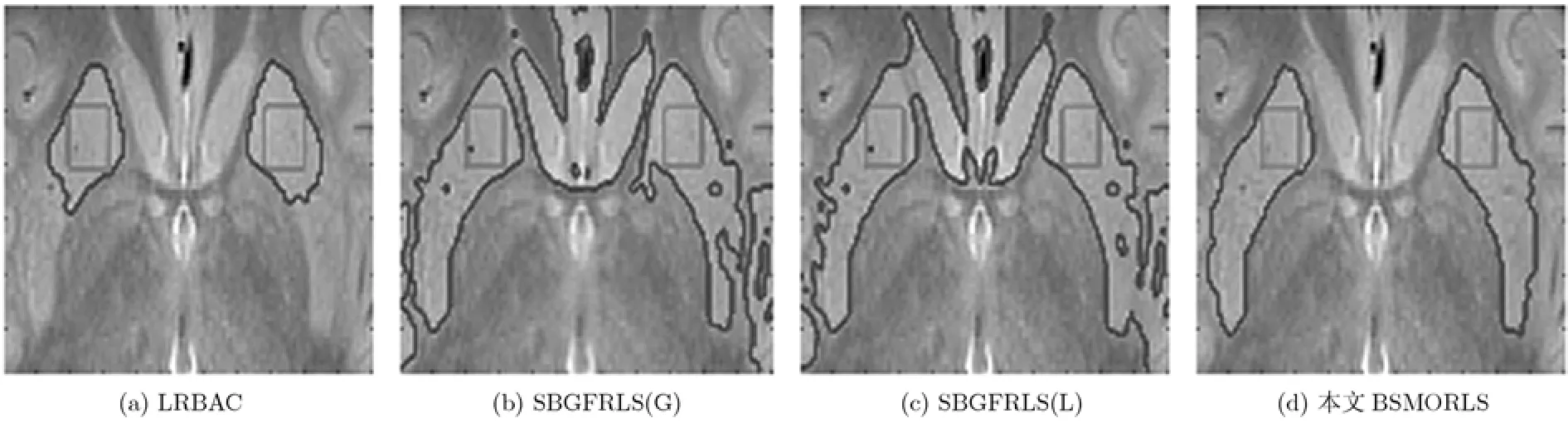
圖8 幾種算法對殼核區域分割對比圖

圖9 不同曲線平滑方案對分割影響對比圖

[1]Jayadevappa D, Kumar S S, and Murty D S. Medical image segmentation algorithms using deformable models: a review[J].IETE Technical Review, 2011, 28(3): 248-255.

[2]Caselles V, Kimmel R, and Sapiro G. Geodesic active contours[J].International Journal of Computer Vision, 1997,22(1): 61-79.

[3]Li C M, Xu C Y, Gui C F,et al.. Distance regularized level set evolution and its application on image segmentation[J].IEEE Transactions on Image Processing, 2010, 19(12):3243-3254.

[4]Chan T and Vese L. Active contour without edges[J].IEEE Transactions on Image Processing, 2001, 10(2): 266-277.

[5]Wang X F, Huang D S, and Xu H. An efficient local Chan-Vese model for image segmentation[J].Pattern Recognition, 2010, 43(3): 603-618.

[6]Lankton S and Tannenbaum A. Localizing region-based active contours[J].IEEE Transactions on Image Processing,2008, 17(11): 2029-2039.

[7]Mille J. Narrow band region-based active contours and surfaces for 2D and 3D segmentation[J].Computer Vision and Image Understanding, 2009, 113(9): 946-965.

[8]胡玉暉. 基于局部子區域的活動輪廓圖像分割方法[J]. 通信技術, 2010, 43(2): 68-70.Hu Yu-hui. Sub-localizing region-based active contours[J].Communications Technology, 2010, 43(2): 68-70.

[9]Zhang K H, Zhang L, Song H H,et al.. Active contours with selective local or global segmentation: a new formulation and level set method[J].Image and Vision Computing, 2010,28(4): 668-676.

[10]Shi Y H, Dong E Q, Li Z Z,et al.. Research on the segmentation of tiny multi-target in brain tissues based on support vector machines[C]. IEEE International Conference on Complex Medical Engineering, Harbin, China, May 22-25,2011: 478-482.

[11]劉曉軍, 董恩清, 呂成林, 等. 磁共振腦部圖像殼核區域有監督蟻群分割算法研究[J]. 中國生物醫學工程學報, 2010, 29(5):683-687.Liu Xiao-jun, Dong En-qing, Lv Cheng-lin,et al.. Supervised segmentation algorithm based on ant colony for putamen region in brain MRI[J].Chinese Journal of Biomedical Engineering, 2010, 29(5): 683-687.

[12]Zhao H K, Chan T, Merriman B,et al.. A variational level set approach to multiphase motion [J].Journal of Computational Physics, 1996, 127(1): 179-195.

[13]Chan T, Esedoglu S, and Nikolova M. Algorithms for finding global minimizers of image segmentation and denoising models [J].Journal on Applied Mathematics, 2006, 66(5):1632-1648.