Mean Shift的漸進(jìn)無(wú)偏變換圖像配準(zhǔn)
楊 烜
(深圳大學(xué)計(jì)算機(jī)與軟件學(xué)院 深圳 518060)
1 引言
圖像配準(zhǔn)的目的是尋找兩幅圖像之間的變換函數(shù),使得圖像中相應(yīng)目標(biāo)的位置對(duì)準(zhǔn)[1]。基于標(biāo)志點(diǎn)對(duì)應(yīng)關(guān)系的圖像配準(zhǔn)方法已得到廣泛使用[2-6],這類方法需要根據(jù)對(duì)應(yīng)點(diǎn)對(duì)構(gòu)造變換函數(shù),變換函數(shù)具有明確的解析式,易于分析,計(jì)算簡(jiǎn)單。但這類變換函數(shù)往往是不可逆的,只能確保標(biāo)志點(diǎn)之間的對(duì)應(yīng)關(guān)系,不能保證圖像間其他位置的對(duì)應(yīng)關(guān)系,即變換的無(wú)偏性較差。
如果變換函數(shù)及其逆變換的Jacobia在1附近對(duì)稱分布,稱為無(wú)偏變換[7]。無(wú)偏變換對(duì)于圖像配準(zhǔn)非常重要,它意味著無(wú)論圖像A向圖像B配準(zhǔn),或是圖像B向圖像A配準(zhǔn)都可以使同一目標(biāo)得到配準(zhǔn)。更重要的是,無(wú)偏變換是拓?fù)浔3值模梢允箞D像在形變前后的拓?fù)潢P(guān)系不發(fā)生變化,這是大多數(shù)圖像配準(zhǔn)方法努力實(shí)現(xiàn)的目標(biāo)[8-10]。目前關(guān)于無(wú)偏變換的研究比較少,文獻(xiàn)[11]定義的對(duì)稱代價(jià)函數(shù),使源圖像和目標(biāo)圖像互換后的變換函數(shù)互逆,但該方法采用FFD形變模型,計(jì)算量較大;文獻(xiàn)[4]提出了標(biāo)志點(diǎn)的一致性配準(zhǔn)方法,該方法可以使標(biāo)志點(diǎn)在正、反變換達(dá)到一致,但會(huì)導(dǎo)致標(biāo)志點(diǎn)對(duì)應(yīng)關(guān)系發(fā)生較大誤差,還需要引入一致性強(qiáng)度配準(zhǔn)進(jìn)一步調(diào)整;文獻(xiàn)[7]定義了變換函數(shù)與理想變換之間的對(duì)稱KL距離,并定義了對(duì)稱目標(biāo)函數(shù)尋找無(wú)偏變換函數(shù),但文獻(xiàn)[7]采用的是粘性流體配準(zhǔn)模型,計(jì)算量仍然很大。
本文針對(duì)基于標(biāo)志點(diǎn)對(duì)應(yīng)關(guān)系的圖像配準(zhǔn)問(wèn)題,提出了一種基于無(wú)偏變換的漸進(jìn)式圖像配準(zhǔn)方法,該方法只需要很少的幾個(gè)初始標(biāo)志點(diǎn),通過(guò)不斷加入新的標(biāo)志點(diǎn)逐漸提高配準(zhǔn)精度。本文從理論上分析了選擇標(biāo)志點(diǎn)的原則,利用Mean Shift迭代快速尋找對(duì)應(yīng)標(biāo)志點(diǎn),構(gòu)造無(wú)偏的變換函數(shù)。本文方法所構(gòu)造的圖像變換函數(shù)既具有較好的無(wú)偏特性,同時(shí)又保證了標(biāo)志點(diǎn)之間的對(duì)應(yīng)關(guān)系。
2 標(biāo)志點(diǎn)分布對(duì)sKL距離的影響
無(wú)偏變換要求變換函數(shù)及其逆變換使圖像被壓縮和被膨脹程度是一致的,我們采用文獻(xiàn)[7]提出的對(duì)稱Kullback-Leibler(sKL)距離來(lái)描述變換的無(wú)偏性。假設(shè)變換函數(shù)為h,逆函數(shù)為h-1,h和h-1的Jacobi行列式分別為定義3種概 率 密 度 函 數(shù) pdfh(ξ)=|Dh(ξ)|,pdfh-1(ξ)=|Dh-1(ξ)|,pdfid(ξ)=1,其中pdfid是單位映射(id(x)的概率密度函數(shù)。對(duì)稱Kullback-Leibler(sKL)距離定義為
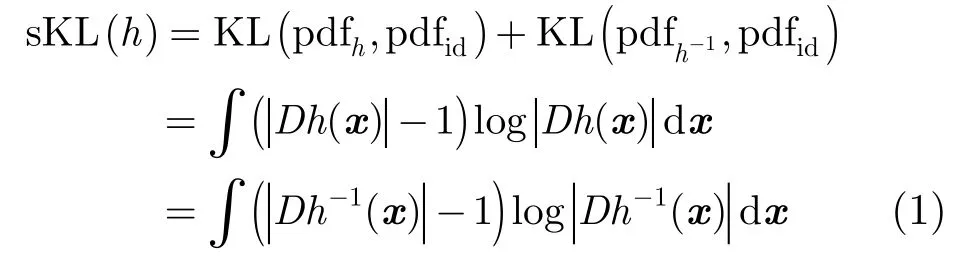
其中KL是Kullback-Leibler距離。尋找無(wú)偏的變換函數(shù),就是使變換函數(shù)的sKL距離盡可能小。對(duì)于基于標(biāo)志點(diǎn)對(duì)應(yīng)關(guān)系的配準(zhǔn)問(wèn)題而言,就是尋找標(biāo)志點(diǎn)對(duì),在配準(zhǔn)精度提高的同時(shí),使變換函數(shù)的sKL距離盡可能小。
假設(shè)源、目標(biāo)點(diǎn)集分別為P和Q,有N對(duì)標(biāo)志點(diǎn)(pi,qi),i=1,2,…,N。pi∈P,qi∈Q,利用徑向基函數(shù)構(gòu)造變換函數(shù),
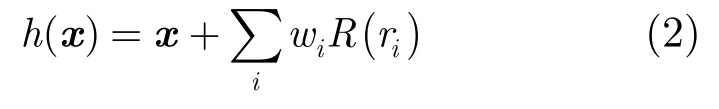
其中x是變換空間中的點(diǎn),R(r)是徑向基函數(shù),ri=||x-pi||,系數(shù)wi,i=1,…,N滿足方程KW=Q-P,K是N×N矩陣,Kij=R(||pi-pj||)。徑向基函數(shù)構(gòu)造的h不能保證可逆,即使其逆函數(shù)h-1存在,h-1與h的壓縮和膨脹程度也有較大差異,即無(wú)偏性較差。
下面我們將在一個(gè)簡(jiǎn)單2維模型上,分析添加標(biāo)志點(diǎn)對(duì)變換函數(shù)sKL的影響。假設(shè)當(dāng)前只有一個(gè)源標(biāo)志點(diǎn)p向右水平移動(dòng)到目標(biāo)點(diǎn)q,水平位移量為d,變換函數(shù)h(x)及其Jacobi行列式Dh(x)為
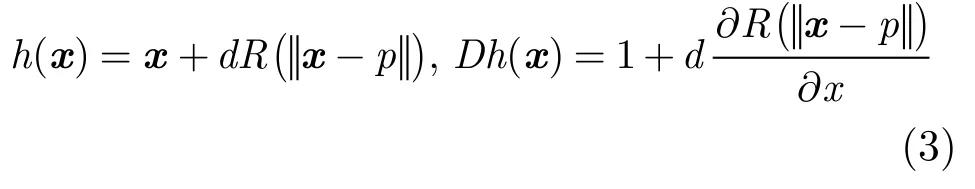
當(dāng)基函數(shù)是單調(diào)減的緊支撐徑向基函數(shù)時(shí),滿足 ?R(r)/ ?r< 0 。不失一般性地以p為原點(diǎn),則x< 0 的點(diǎn)(p左側(cè)區(qū)域)Jacobi值大于1,而x>0(p右側(cè)區(qū)域)Jacobi值小于1。在點(diǎn)p的垂直上方L處添加點(diǎn)pa,該點(diǎn)水平位移至qa,假設(shè)位移量為dR( | |pa-p| | )+ε,其中dR( ||pa-p| |)是根據(jù)原變換函數(shù)h(x)對(duì)pa的位移量,ε是該位移的小擾動(dòng)。則新的變換函數(shù)ha(x)為
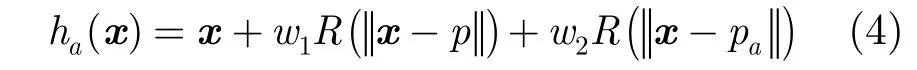
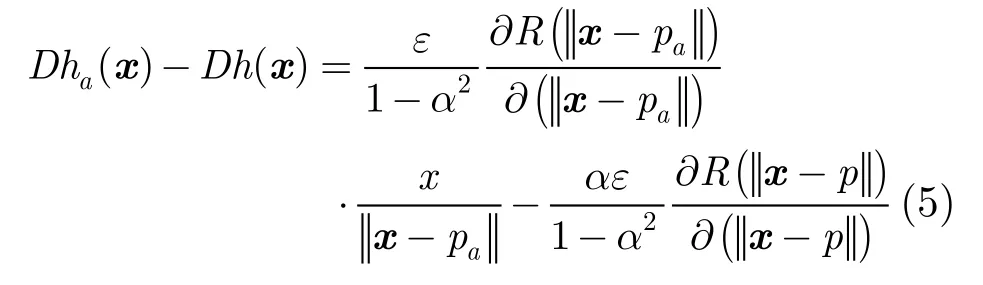
當(dāng)L相對(duì)基函數(shù)的支撐集較小時(shí),式(5)可以近似為

我們以緊支撐薄板樣條(CSTPS)[5]作為徑向基函數(shù)進(jìn)行分析,可以推出
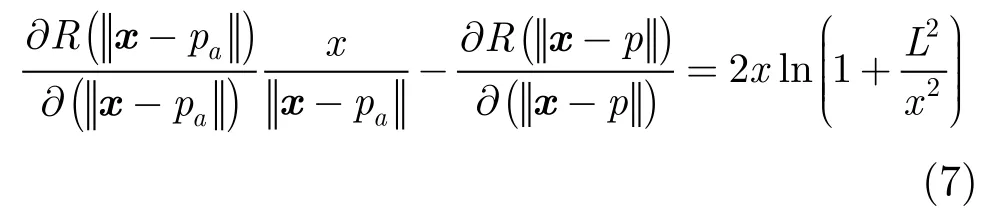
式(7)表明,新增點(diǎn)可以使x>0的點(diǎn)Jacobi值增加,x<0的 Jacobi值減小,這意味著通過(guò)添加點(diǎn),在點(diǎn)p兩側(cè)的Jacobi值更接近1,即變換函數(shù)的無(wú)偏性改善了。需要說(shuō)明的是,擾動(dòng)ε不能過(guò)大,否則調(diào)整量會(huì)過(guò)大,可能會(huì)使變換函數(shù)的無(wú)偏性變差。上述分析中對(duì)于新增標(biāo)志點(diǎn)pa的位置并沒(méi)有嚴(yán)格的限制,一般地講,我們需要在原標(biāo)志點(diǎn)附近選擇新增點(diǎn),并且新增點(diǎn)的位移與原變換函數(shù)產(chǎn)生的位移是一致,即新加點(diǎn)的對(duì)應(yīng)點(diǎn)選擇在原變換函數(shù)的映射位置附近,這樣該點(diǎn)的位移趨勢(shì)與原變換函數(shù)近似,以滿足ε較小的條件。另一方面,L較小也意味著將在較小的范圍內(nèi)搜索對(duì)應(yīng)標(biāo)志點(diǎn),有利于尋找到準(zhǔn)確的對(duì)應(yīng)點(diǎn)。
對(duì)于圖像配準(zhǔn)問(wèn)題,上述的要求可以這樣理解:當(dāng)原始變換函數(shù)的無(wú)偏性需要改善時(shí),可以在原標(biāo)志點(diǎn)的附近添加新增標(biāo)志點(diǎn),新增標(biāo)志點(diǎn)的選擇原則是以圖像配準(zhǔn)精度得到提高為依據(jù),這樣新增標(biāo)志點(diǎn)可以對(duì)變換函數(shù)的無(wú)偏性起到改善作用。描述得更形象一些,當(dāng)形變曲面被某些位移撕扯時(shí),由于這種撕扯的受力不夠均勻,會(huì)使圖像在這些撕扯位置附近出現(xiàn)過(guò)度擠壓或膨脹的情況。通過(guò)增加標(biāo)志點(diǎn),可以使撕扯效果得到緩解,變得平滑和均勻,變換函數(shù)的無(wú)偏性得到改善。
3 Mean Shift確定新增標(biāo)志點(diǎn)對(duì)
假設(shè)S,R分別是源圖像和參考圖像,當(dāng)前源標(biāo)志點(diǎn)集為P,目標(biāo)標(biāo)志點(diǎn)集為Q,標(biāo)志點(diǎn)對(duì)集合為?pi∈P,選擇新增源標(biāo)志點(diǎn)滿足
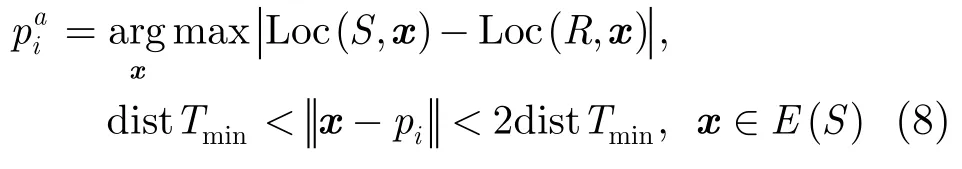
其中 L oc(I,x)是圖像I中以x為中心的局部區(qū)域,E(S)是源圖像S的邊緣點(diǎn)集合。新增源標(biāo)志點(diǎn)處于邊緣上,其所處的區(qū)域與參考圖像相差較大。同時(shí)該點(diǎn)與當(dāng)前標(biāo)志點(diǎn)的距離不能太遠(yuǎn),這樣可以利用當(dāng)前標(biāo)志點(diǎn)提供一個(gè)較理想的初始位置,有利于Mean Shift迭代收斂;同時(shí)也不能距離過(guò)近,以免局部形變受力不勻。
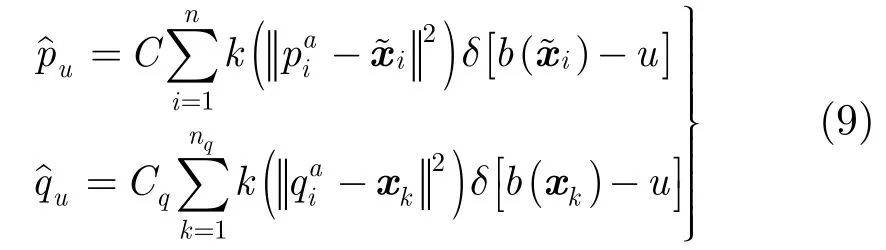
其中k(x)是核函數(shù),分別是以為中心的鄰域點(diǎn),是歸一距離,C和Cq是歸一系數(shù),u是灰度量化值,b(x)是量化函數(shù),本文采用直方圖模糊約束聚類方法進(jìn)行量化。根據(jù)Mean Shift迭代,更新為
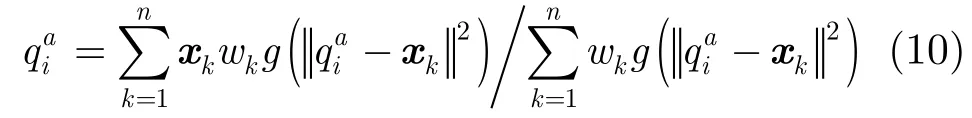

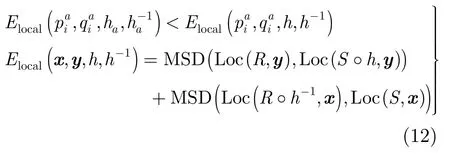
由于Mean Shift收斂是基于概率密度函數(shù)變化最大方向進(jìn)行的,容易收斂于局部最優(yōu)。需要對(duì)Mean Shift進(jìn)行幾點(diǎn)改進(jìn)。首先進(jìn)行多尺度配準(zhǔn),將配準(zhǔn)圖像下采樣到大尺度圖像上進(jìn)行Mean Shift收斂,可以減小搜索范圍。將大尺度圖像的標(biāo)志點(diǎn)對(duì)映射到小尺度圖像中,得到粗配準(zhǔn)結(jié)果。然后在小尺度圖像中重復(fù)這個(gè)配準(zhǔn)過(guò)程,得到精度更好的配準(zhǔn)結(jié)果。
其次,由于Mean Shift統(tǒng)計(jì)的概率密度是不反映圖像空間位置信息的,Mean Shift收斂后對(duì)應(yīng)的點(diǎn),可能并不是使局部圖像空間對(duì)應(yīng)關(guān)系最優(yōu)的點(diǎn)。本文在Mean Shift迭代的路徑中計(jì)算各點(diǎn)的局部配準(zhǔn)度量,選擇局部配準(zhǔn)度量最大的點(diǎn)作為收斂結(jié)果,以提高對(duì)應(yīng)點(diǎn)精度。另外,Mean Shift迭代路徑要進(jìn)行限制,以避免沿某個(gè)錯(cuò)誤方向迭代過(guò)遠(yuǎn)。
在一個(gè)尺度下的完整配準(zhǔn)過(guò)程如下:
步驟 1 輸入源圖像和參考圖像,初始標(biāo)志點(diǎn)對(duì)集合Ω,設(shè)置參數(shù) d istThmin,Th,支撐集c。
步驟 2 利用式(2)計(jì)算Ω的變換函數(shù)h(x)。
步驟 3 如果 d istTmin>T h,則算法退出,否則
步驟 4 ?pi∈P,確定滿足式(8)的新增源標(biāo)志點(diǎn)。
步驟 7 計(jì)算Ω∪Ωa的變換函數(shù)ha(x)和,以及代價(jià)函數(shù)。
步驟 9 如果集合Ω沒(méi)有增大,則 d istTmin=distTmin+ 1 。轉(zhuǎn)至步驟3。
4 實(shí)驗(yàn)結(jié)果
分別針對(duì)大形變和小形變配準(zhǔn)進(jìn)行實(shí)驗(yàn)驗(yàn)證。圖1中第1、第2行是Rose和Clown的大形變配準(zhǔn),分別選擇了4個(gè)和7個(gè)初始標(biāo)志點(diǎn)對(duì),采用CSTPS作為徑向基函數(shù),支撐集c=200,d istTmin= 8,Th=16。圖像大小均為 256×256,將圖像下采樣為128×128,進(jìn)行大尺度配準(zhǔn),再進(jìn)行小尺度配準(zhǔn)。其中Rose圖、Clown圖中各添加了142, 92對(duì)標(biāo)志點(diǎn),可以看出, Rose的邊界部分和Clown的帽沿這些形變劇烈的地方都得到了較好的配準(zhǔn)。
為了比較配準(zhǔn)效果,本文同時(shí)通過(guò)SIFT特征[13]確定對(duì)應(yīng)標(biāo)志點(diǎn),將位移大于32的嚴(yán)重誤配標(biāo)志點(diǎn)對(duì)剔除。SIFT標(biāo)志點(diǎn)對(duì)應(yīng)關(guān)系的閾值設(shè)為使變換函數(shù)Jacobi值大于0的最大值,以盡可能多地保留標(biāo)志點(diǎn)對(duì)。SIFT在Rose圖和Clown圖中分別添加了42和31對(duì)標(biāo)志點(diǎn),SIFT在Clown中尋找的標(biāo)志點(diǎn)對(duì)存在誤差,無(wú)法得到Jacobi值大于0的變換結(jié)果。這表明 SIFT不適用于形變比較劇烈的彈性配準(zhǔn)問(wèn)題,而本文方法具有較好的魯棒性。
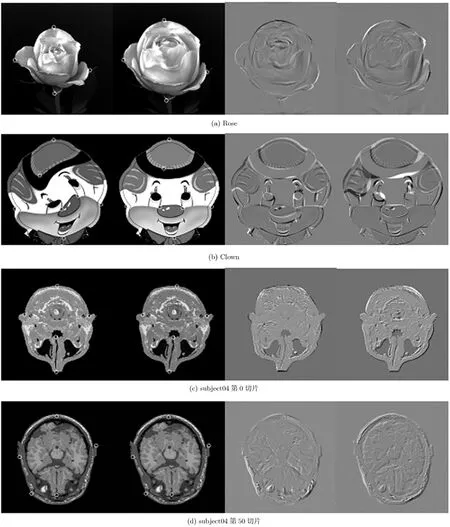
圖1 將源圖像配準(zhǔn)到參考圖像的實(shí)驗(yàn)結(jié)果(從左到右:待配圖像,參考圖像,本文方法配準(zhǔn)結(jié)果與參考圖像的差,SIFT配準(zhǔn)結(jié)果與參考圖像的差)
小形變配準(zhǔn)采用了人體腦部掃描切片,待配準(zhǔn)圖像源于BrainWeb的subject04個(gè)體的腦部體數(shù)據(jù)切片,分別是第0和第50切片,經(jīng)過(guò)人工小形變,得到參考圖像。第0和第50切片中各選擇了5對(duì)初始標(biāo)志點(diǎn)。這兩幅配準(zhǔn)圖像的細(xì)節(jié)比較豐富,特別是腦切片中部區(qū)域?qū)ε錅?zhǔn)要求較高,本文方法在第0,第50切片分別增加了110, 123對(duì)標(biāo)志點(diǎn),并且在腦中部區(qū)域確定了多個(gè)精度較高的標(biāo)志點(diǎn),提高了這些區(qū)域的配準(zhǔn)精度,而SIFT在第0,第50切片中各新增65和308對(duì)標(biāo)志點(diǎn),但這些標(biāo)志點(diǎn)中有許多點(diǎn)幾乎重合,而在腦切片中部區(qū)域選擇的標(biāo)志點(diǎn)較少,分布也不均勻,導(dǎo)致這些區(qū)域配準(zhǔn)精度不高。表1列出了本文方法和SIFT配準(zhǔn)結(jié)果的互信息、均方差(MSD)、相關(guān)系數(shù)(CC)和sKL距離,加粗的數(shù)值表示最優(yōu)結(jié)果。從表1可以看出,對(duì)于小形變配準(zhǔn)問(wèn)題,本文配準(zhǔn)結(jié)果同樣優(yōu)于 SIFT方法的結(jié)果,同時(shí)sKL距離表明,本文方法得到的變換函數(shù)的無(wú)偏性優(yōu)于SIFT方法。
5 結(jié)論
本文針對(duì)標(biāo)志點(diǎn)對(duì)應(yīng)關(guān)系的圖像配準(zhǔn)問(wèn)題,提出了一種漸進(jìn)式無(wú)偏變換的配準(zhǔn)方法。首先人為選擇數(shù)量極少的幾個(gè)初始標(biāo)志點(diǎn),在初始標(biāo)志點(diǎn)附近添加適當(dāng)?shù)臉?biāo)志點(diǎn),利用Mean Shift迭代尋找相應(yīng)的對(duì)應(yīng)點(diǎn);根據(jù)新標(biāo)志點(diǎn)對(duì)判定配準(zhǔn)度量的變化,確定需要添加到標(biāo)志點(diǎn)集合的新標(biāo)志點(diǎn)對(duì);在擴(kuò)展的標(biāo)志點(diǎn)集合中繼續(xù)利用Mean Shift迭代尋找對(duì)應(yīng)標(biāo)志點(diǎn),逐步達(dá)到配準(zhǔn)的效果。該方法中尋找對(duì)應(yīng)標(biāo)志點(diǎn)的過(guò)程充分考慮了變換無(wú)偏性的影響,同時(shí)為Mean Shift收斂提供了較準(zhǔn)確的初始位置,多尺度的配準(zhǔn)策略有利于魯棒地尋找到準(zhǔn)確的對(duì)應(yīng)點(diǎn)。實(shí)驗(yàn)比較結(jié)果表明本文方法不僅適用于大形變配準(zhǔn)問(wèn)題,也可以用于解決小形變問(wèn)題,是一種魯棒的配準(zhǔn)方法。

表1 配準(zhǔn)結(jié)果比較(N/A表示變換函數(shù)拓?fù)洳荒鼙3?
[1]Rueckert D and Aljabar P. Nonrigid registration of medical images: theory, methods, and applications.IEEE Signal Processing Magazine, 2010, 27(4): 113-119.
[2]Myronenko A and Song X B.Intensity-based image registration by minimizing residual complexity.IEEE Transactions on Medical Imaging, 2010, 29(11): 1882-1891.
[3]Chen J, Tian J, Lee N,et al.. A partial intensity invariant feature descriptor for multimodal retinal image registration.IEEE Transactions on Biomedical Engineering, 2010, 57(7):1707-1718.
[4]Johnson H J and Christensen G E. Consistent landmark and intensity-based image registration.IEEE Transactions on Medical Imaging, 2002, 21(5): 450-461.
[5]Zhang Z X and Yang X. Elastic image warping using a new radial basic function with compact support. Proceedings of International Conference on Bio-inspired Systems and Signal Processing 2008, Funchal, Madeira, Portugal, January 28-31,2008: 216-219.
[6]Shen D and Davatzikos C. HAMMER: hierarchical attribute matching mechanism for elastic registration.IEEE Transactions on Medical Imaging, 2002, 21(11): 1421-1439.
[7]Leow A D, Yanovsky I, Chiang M C,et al.. Statistical properties of Jacobian maps and the realization of unbiased large-deformation nonlinear image registration, 2007, 26(6):822-832.
[8]Lin X B, Qiu T S, Morain-Nicolier F,et al.. A topology preserving non-rigid registration algorithm with integration shape knowledge to segment brain subcortical structures from MRI images.Pattern Recognition, 2010, 43(7):2418-2427.
[9]Sdika M. A fast nonrigid image registration with constraints on the Jacobian using large scale constrained optimization.IEEE Transactions on Medical Imaging, 2008, 27(2): 271-281.
[10]Noblet V, Heinrich C, Heitz F,et al.. 3-D deformable image registration: a topology preservation scheme based on hierarchical deformation models and interval analysis optimization.IEEE Transactions on Image Processing, 2005,14(5): 553-566.
[11]Gholipour A, Kehtarnavaz N, Yousefi S,et al.. Symmetric deformable image registration via optimization of information theoretic measures.Image and Vision Computing,2010, 28(6): 965-975.
[12]Comaniciu D, Ramesh V, and Meer P. Real-time tracking of non-rigid objects using mean shift. Proceedings of IEEE Conference Computer Vision and Pattern Recognition, Los Alamitos: IEEE Computer Society Press, 2000: 142-149.
[13]Lowe D G. Distinctive image features from scale-invariant keypoints.International Journal of Computer Vision, 2004,60(2): 91-110.

