“三步”巧數食物鏈——“找岔路相加法”

徐建蕓

由于食物鏈和食物網能夠將生態系統及相關重要知識聯系起來，成為生物學科綜合題型的良好載體，所以一直是高考的重點和難點，計算食物網中食物鏈的條數就是其中常考點之一。對于生態系統中營養結構復雜的食物網，考生們經常會出現丟三落四、或多或少的情況。

同時筆者在教學過程中也曾遇到相關知識點進退兩難的窘境。在必修三課本P91的教材圖片處理的過程中，突然有學生問這么錯綜復雜的食物網總共有幾條食物鏈。于是為滿足他們的好奇心，讓他們用傳統的方法自己數，最后眼看著時間一分一秒地流逝卻沒有得到正確的結果。以前對于這類數量多、耗時長、難度大的食物網，在課堂中教師一般不想也不敢讓學生體驗。于是筆者通過查閱資料、探索歸納并總結出一種行之有效、方便快捷、容易掌握的方法——“找岔路相加法”。

1 “找岔路相加法”的原理和方法

食物鏈之所以能形成食物網，是因為某種生物可能以多種生物為食物，且該生物也可能成為多種生物的食物，因此以該生物為中心就形成了食物網中一個錯綜復雜、有進有出的“岔口”。食物網中“岔口”的復雜程度不同，有一進多出、多進一出以及多進多出等等。

（1）找出食物網中的所有生產者，并計數出流入下一營養級的“岔路”條數。因為食物鏈的起點是生產者，而且生產者流入下一營養級的“岔路”有幾條，該食物網中的食物鏈就至少有幾條，并通過后面的“結”增加。

（2）食物網中的各級消費者按以下類型分類討論：

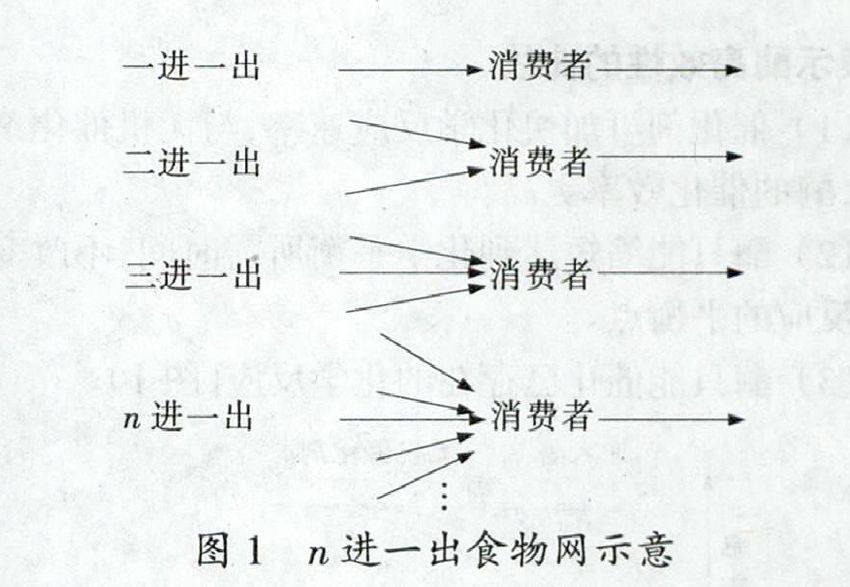
①n進一出（含一條“岔路”）。

如圖1中，由于一條完整的食物鏈必須從生產者開始數到此鏈的最高營養級生物為止，所以該類型中唯一的“岔路”本就已經和它的每一條“來源”（實際上是上一級的去路）同屬于一條食物鏈上。由于這些食物鏈在上一級生物時已經計數，因此該類型的“結”未有新的食物鏈增加。故當消費者只含有一條“岔路”時，此處食物鏈的條數不增加，此類型不需要篩選出來參與最后的相加。

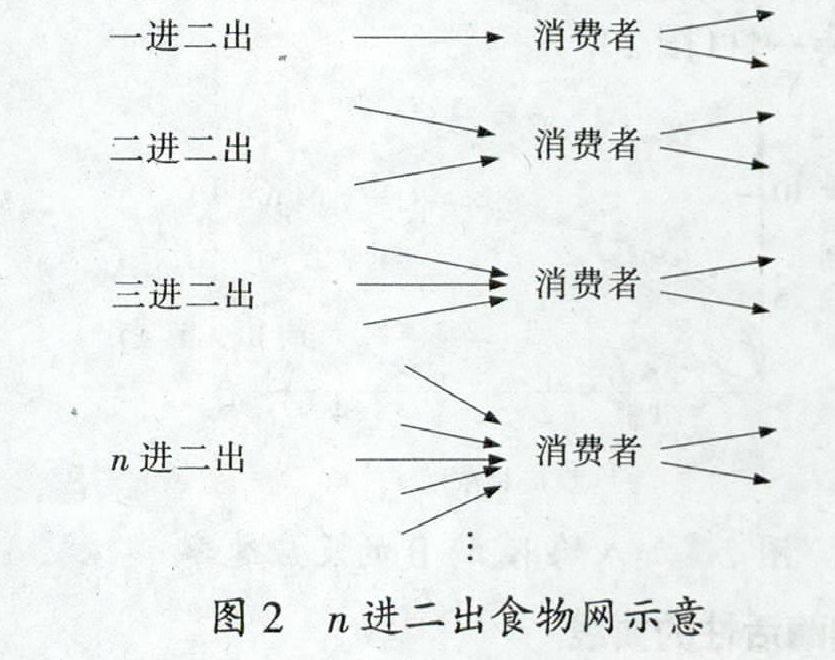
②n進二出（含兩條“岔路”）。

如圖2中，該類型“結”的兩條“岔路”中有一條和每一個“來源”也已屬同一條食物鏈上（如1→1，2→1），此處新增加的食物鏈是另一條“去路”和每一個“來源”分別產生的（如1→2，2→2）。以此類推，n進二出的類型中新增加的食物鏈條數為：nx（2—1）。所以當消費者含有兩條“岔路”時，需要將其篩選出，并按照上述規律計算結果與其他個體相加。

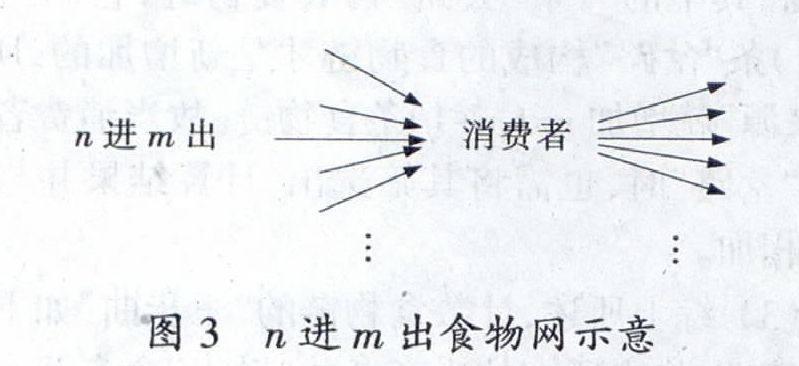
③n進m出（含多條“岔路”）

如圖3中，根據上面的分析發現：每一條“來源”都已和其中的一條“去路”構成食物鏈，它們與其余（m-1）條“岔路”構成的食物鏈才是新增加的，所有n條“來源”就增加nx（m-1）條食物鏈。故當消費者含有多條“岔路”時，也需將其篩選出，計算結果并與其他個體相加。

（3）綜上所述，計數食物鏈的“三步曲”如下。第一步篩選：找出所有的生產者并“揪出”含有兩個及兩個以上“岔路”的各級消費者。第二步計算：數出所有生產者的“岔路”的條數，對于篩選出的消費者，根據它們所組成的“結”是幾進幾出的具體情況進行計算新增加的食物鏈數目，若某消費者組成的“結”為n進m出，則該“結”處新增加的食物鏈數為nx（m—1）。第三步相加：將以上生物的計算結果相加，所得之和即為食物網中所有食物鏈的條數。

學生能準確掌握“找岔路相加法”的原理和方法，并加以熟練運用，以后不管遇到多么復雜的食物網，都能夠迅速而準確地計算出其中食物鏈的數目，尤其，是在考試甚至高考中贏得時間和分數。