六相感應電動機調速系統的建模與仿真

屈魯，謝衛，盧穎娟，張貽旭

(上海海事大學物流工程學院，上海 201306)

0 引言

電力電子技術的發展，使得三相感應電動機的變頻調速技術得到廣泛應用.但是，三相感應電動機系統可靠性不足，只要有一相出現故障，就會導致系統崩潰;并且在大功率場合下，由于功率開關器件的串并聯會出現不均壓和不均流等一系列問題.與三相感應電動機系統相比，多相感應電動機系統在許多方面，尤其是在大功率場合具有突出的優勢.在電動機容量一定和相電流不變的情況下，隨著電動機定子相數的增加，所需供電電壓降低，可用低壓功率器件實現大功率，避免由功率器件串并聯帶來的問題.此外，對于多相感應電動機系統，當其中一相或多相退出運行或缺相運行時，系統無須停機，仍然可以穩定運行，系統運行可靠性提高.目前，多相感應電動機及其調速系統在電動汽車、船艦推進、航空航天等領域的研究和實踐日益增加.［1－2］

本文主要研究六相感應電動機調速系統的建模及仿真.六相感應電動機的轉子繞組仍為常見的鼠籠結構，定子繞組采用兩組互差30°電角度的對稱三相繞組構成的六相雙Y型結構.若將鼠籠形轉子繞組也等效為類似的六相雙Y型繞組，則六相感應電動機的物理模型可用圖1表示.研究表明，采用這種繞組結構可以有效削弱轉矩脈動，大幅度減小電機的損耗，提高電動機的極限容量.

1 六相感應電動機的數學模型

為便于分析，同時也滿足工程實際所需的精度要求，可作如下假設:

(1)定子、轉子表面光滑，無齒槽效應，氣隙均勻;

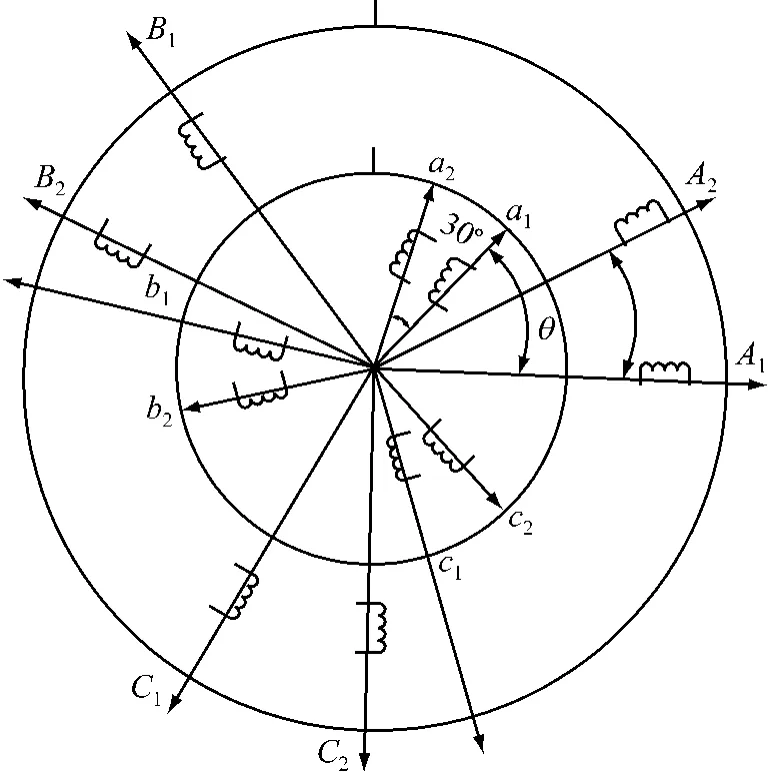
圖1 六相感應電動機的物理模型

(2)不計鐵磁飽和、磁滯、渦流影響及導體趨膚效應;

(3)氣隙磁場正弦分布，忽略磁場高次諧波的影響.

1.1 三相靜止A－B－C坐標系的數學模型

根據上述假設條件，由六相感應電動機的物理模型及電磁關系，可得其在三相靜止A－B－C坐標系下的數學模型［3－4］.

1.1.1 磁鏈方程

六相感應電動機在A－B－C坐標系下的磁鏈方程為

式中:ψs為定子磁鏈向量;ψr為轉子磁鏈向量;is為定子電流向量;ir為轉子電流向量;Lss為定子自感矩陣;Lrr為轉子自感矩陣;Lsr=LrsT為定、轉子互感矩陣.

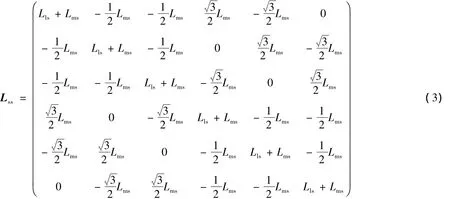
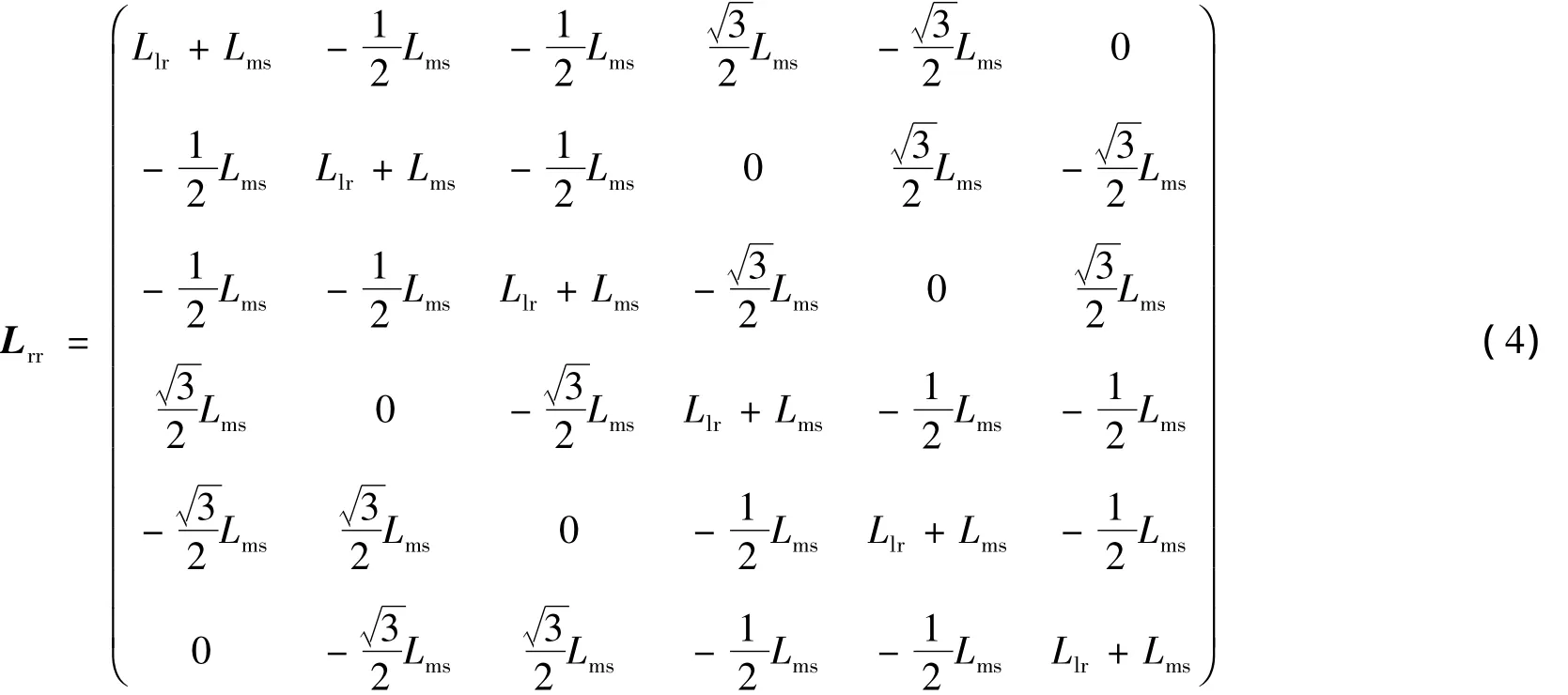
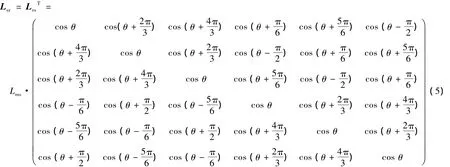
式中:Lls為定子等效兩相繞組的自感;Llr為轉子等效兩相繞組的自感;Lms為定子與轉子同軸等效繞組間的互感;θ為轉子a1相與定子A1相之間的夾角.

1.1.2 電壓方程

六相感應電動機在A－B－C坐標系下的電壓方程為

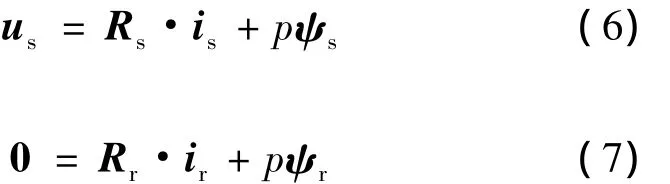
式中:us為定子電壓向量;Rs為定子電阻矩陣;Rr為轉子電阻矩陣.

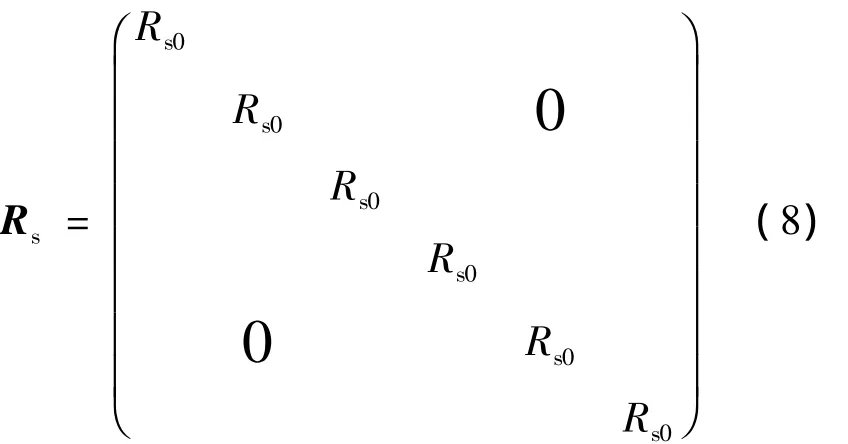
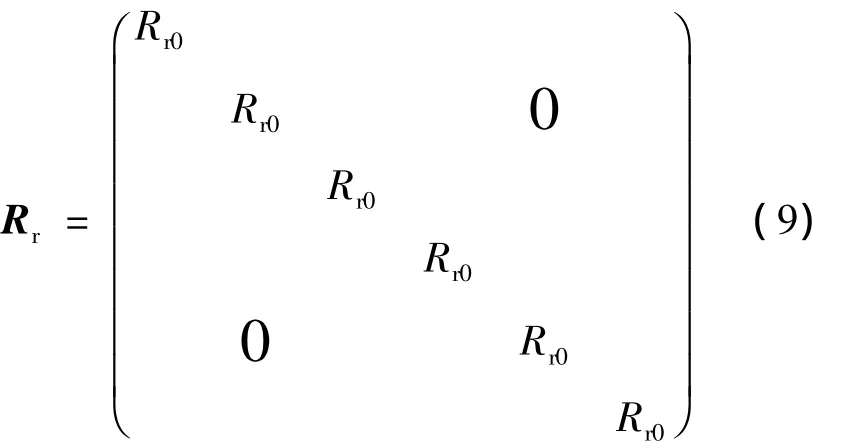
式中:Rs0是定子每相電阻;Rr0是轉子每相電阻.

1.1.3 轉矩方程與運動方程

六相感應電動機在A－B－C坐標系下的轉矩方程為

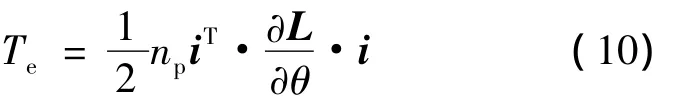
若忽略電力拖動系統傳動機構中的黏滯性摩擦和扭轉彈性，則六相感應電動機在A－B－C坐標系下的運動方程為

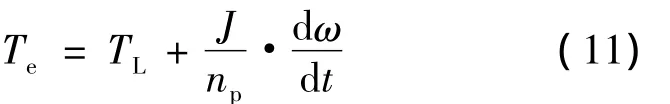
式中:TL為負載轉矩;ω為轉子角速度.

1.2 兩相旋轉d－q坐標系的數學模型

六相感應電動機在A－B－C坐標系下的數學模型是一個高階、非線性、強耦合的多變量系統，可以通過坐標變換對其進行降階、化簡，由此建立六相感應電動機在d－q坐標系下的數學模型.滿足功率不變和磁動勢不變的變換矩陣及其逆矩陣［5］如下:

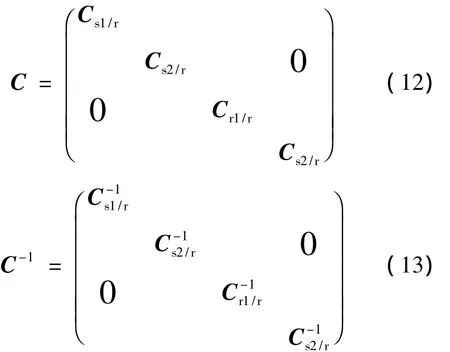
其中:

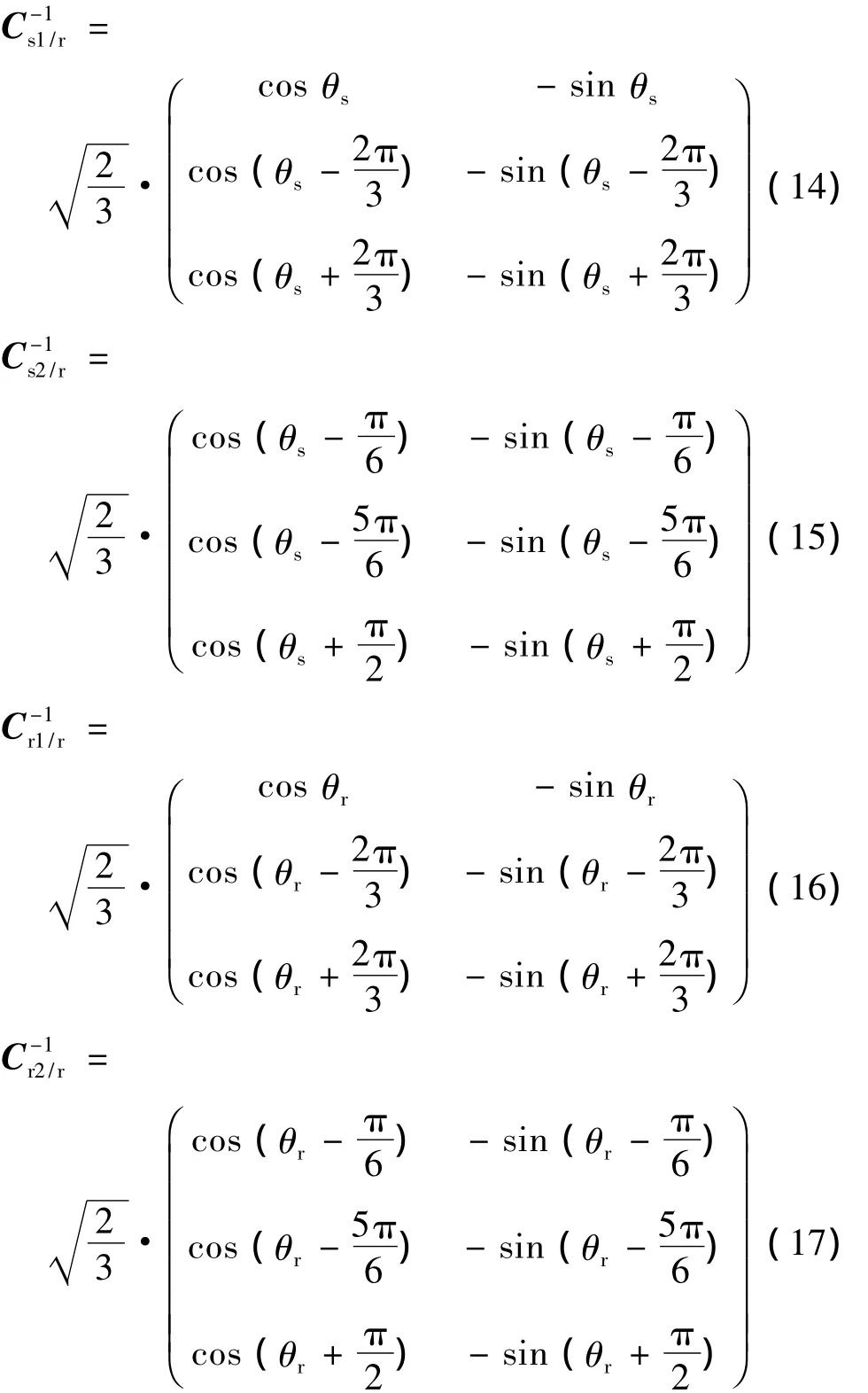
式中:θs為d軸與A1軸之間的夾角;θr為d軸與a1軸之間的夾角.

1.2.1 磁鏈方程

六相感應電動機在d－q坐標系下的磁鏈方程為

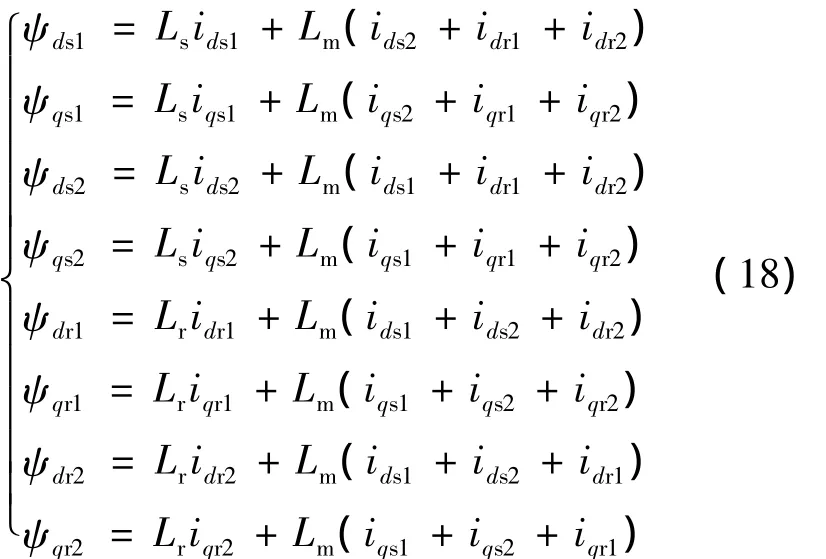
式中:Lm=1.5Lms，為d－q坐標系同軸定子與轉子等效繞組間互感;Ls=1.5Lms+Lls，為 d－q坐標系定子等效兩相繞組自感;Lr=1.5Lms+Llr，為 d－q坐標系轉子等效兩相繞組自感.

1.2.2 電壓方程

六相感應電動機在d－q坐標系下的電壓方程為

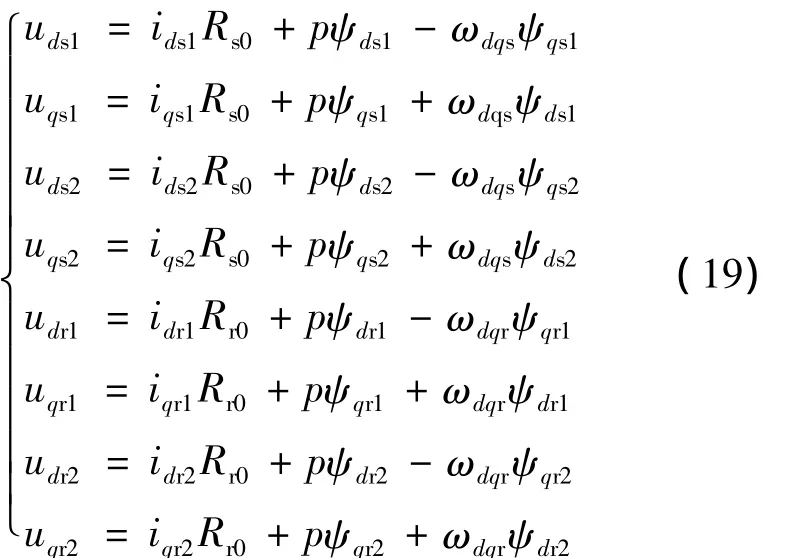
式中:ωdqs為d－q坐標系相對于定子A1相的角轉速;ωdqr為d－q坐標系相對于轉子a1相的角轉速.

1.2.3 轉矩方程與運動方程

六相感應電動機在d－q坐標系下的轉矩方程為

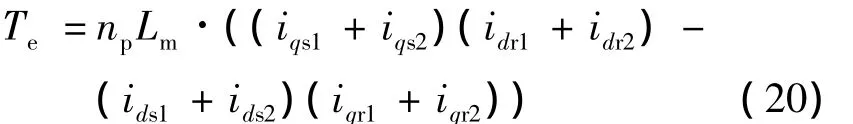
運動方程為

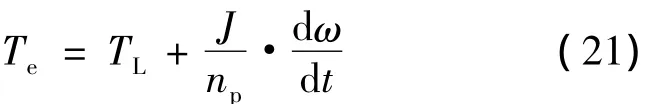
2 SVPWM技術

六相感應電動機采用電壓源型逆變器供電時，定子電流諧波較大，這是因為定子繞組的阻抗較小.解決這一問題的有效方法是采用空間矢量脈寬調制(Space Vector Pulse Width Modulation，SVPWM)技術.

六相感應電動機定子采用雙Y型繞組，其中定子繞組A1，B1，C1可由圖2所示的六相橋式電壓源型逆變電路的(一)組逆變電路供電;定子繞組A2，B2，C2由逆變電路的(二)組供電.［6］

圖2 六相橋式電壓源型逆變電路

當進行SVPWM時，可采用兩組相位差為30°電角度的三相對稱正弦波作為調制信號和同一個三角載波信號進行調制，生成兩組觸發脈沖控制逆變器上器件的通斷，由此產生兩組相位差互為30°電角度的SVPWM波，其基本電壓空間矢量分布見圖3.

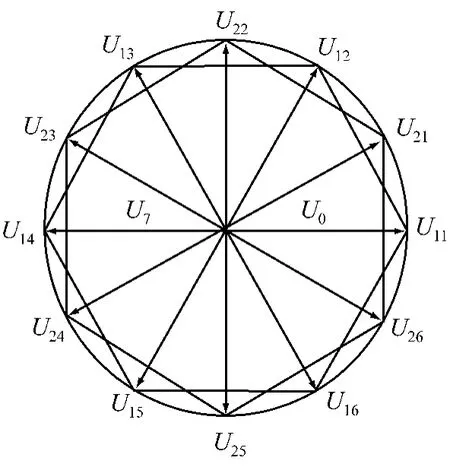
圖3 六相逆變器SVPWM基本電壓空間矢量分布

3 MATLAB建模及仿真

3.1 SVPWM電壓源型逆變器的建模仿真

按照上述SVPWM原理，在SIMULINK環境下建立SVPWM六相電壓源型逆變器的仿真模型并進行仿真，有關參數:直流電壓1 000 V，正弦波頻率50 Hz，三角波頻率1 860 Hz.仿真所得的逆變器輸出相電壓波形見圖4.

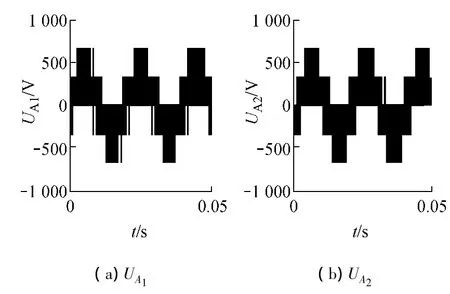
圖4 逆變器輸出電壓UA1和UA2

3.2 六相感應電動機調速系統的建模仿真

根據六相感應電動機在d－q坐標系下的數學模型，在SIMULINK環境下建立基于兩相同步旋轉坐標系下的六相感應電動機仿真模型，主要包括電壓、磁鏈和轉矩等3個子模塊，見圖5.由SVPWM六相電壓源型逆變器供電，進行電動機起動和回饋制動的仿真.

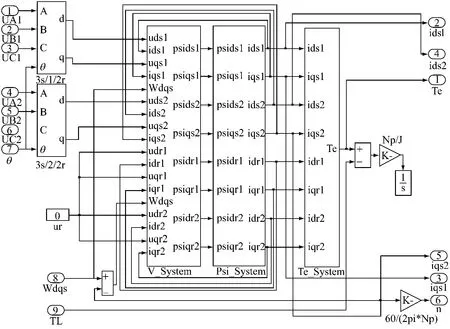
圖5 六相感應電動機的仿真模型

六相感應電動機額定數據如下:np=3，f1=50 Hz，Rs=0.22 Ω，Rr=0.47 Ω，Ls=0.039 5 H，Lr=0.039 5 H，Lm=0.036 4 H，J=0.116 N·m2.3.2.1 起動仿真

令負載轉矩為零，仿真結果見圖6.

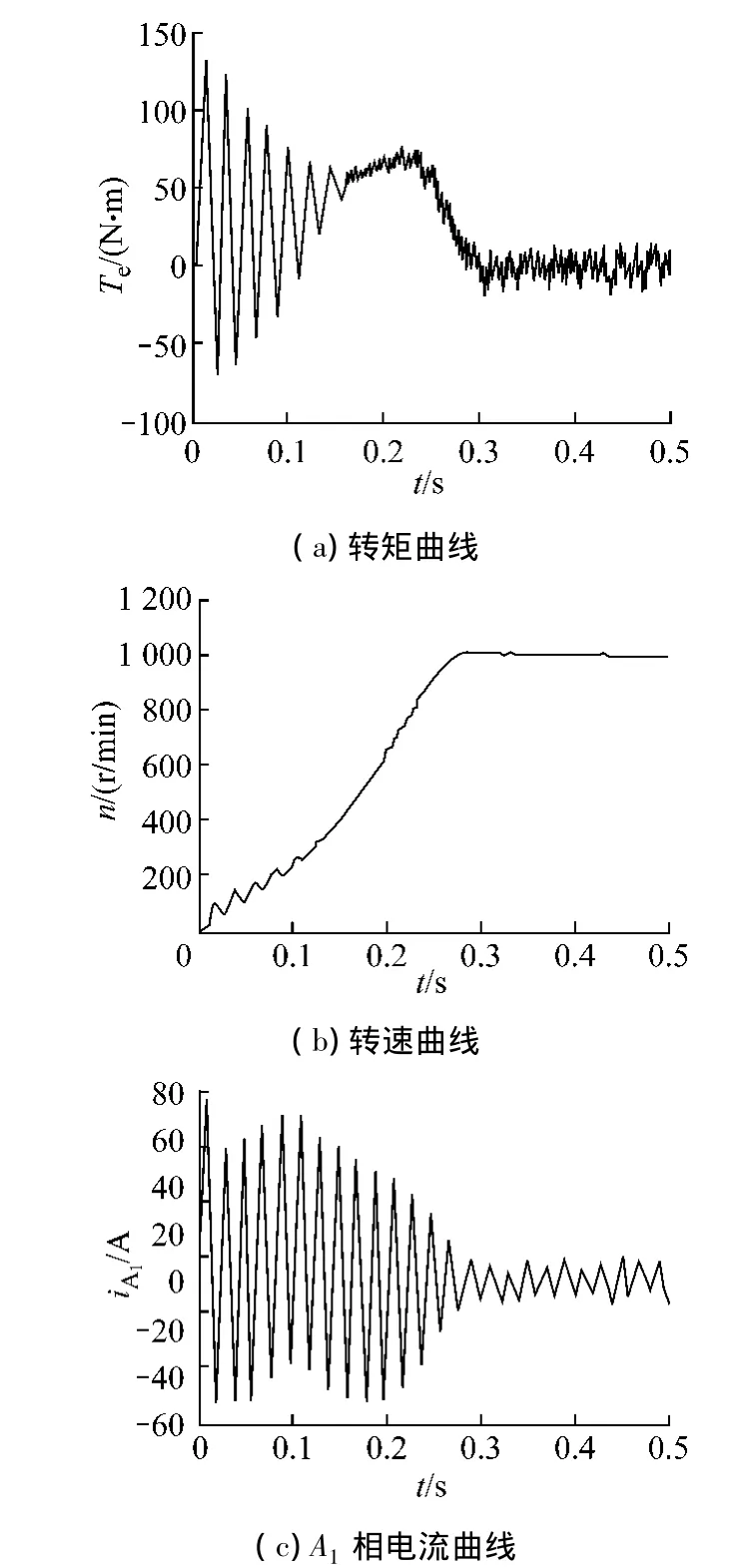
圖6 起動仿真結果

由仿真結果可知，空載直接起動只需0.3 s，轉速就穩定在同步轉速上.

3.2.2 回饋制動仿真

當電動機空載運行0.5 s之后，將負載轉矩改成負值，進入回饋制動過程，仿真結果見圖7.

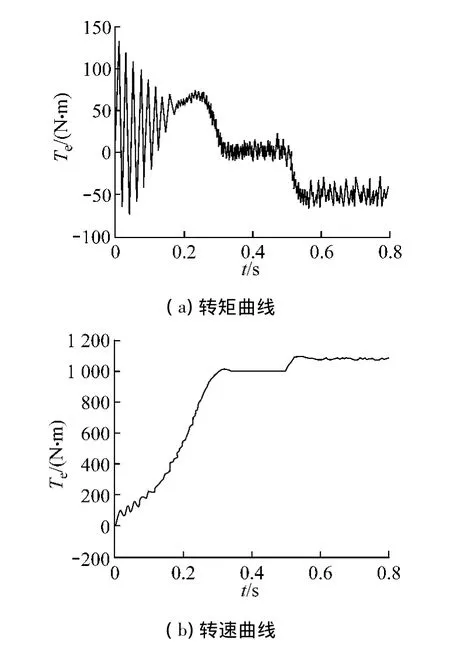
圖7 回饋制動仿真結果

由仿真結果可知，當電機轉速超過同步轉速時，電機進入發電狀態，向電網回饋電能，僅需0.1 s就達到穩定，動態性能好.

4 結束語

在MATLAB/SIMULINK環境下，建立SVPWM六相電壓源型逆變器供電的六相感應電動機調速系統的數學模型和仿真模型，并在此基礎上分別進行直接空載起動和回饋制動的動態仿真.通過仿真結果分析，可知六相感應電動機調速系統具有較好的的動態性能和穩態性能.

［1］SMIRANDA R，JACOBINA C B，LIMA A M N.Modeling and analysis of six－phase induction machine under fault condition［J］.IEEE Trans on Energy Applications，2009，4(9):824－829.

［2］金愛娟，李少龍，任永德，等.六相感應電機的SVPWM技術研究［J］.測控技術，2004，23(6):40－42.

［3］LIN Chen，FAN Yang.Unified voltage modulation method for dual three－phase induction machine［J］.IEEE Proc 3rd Int Conf Machine Learning ＆Cybernetics，2004，26(29):672－677.

［4］李山，王明渝，劉和平.基于DSP的六相感應電機矢量控制系統設計［J］.大電機技術，2005(3):23－26.

［5］陳伯時.電力拖動自動控制系統［M］.3版.北京:機械工業出版社，2003:63－270.

［6］ZHAO Y，LIPO T A.Space vector PWM control of dual three－phase induction machine using vector space decomposition［J］.IEEE Trans Industry Applications，1995，31(5):1100－1109.