一類含有參數的Euler和的閉形式

晉慧峰，張明學

（太原理工大學 數學學院，太原030024）

關于古典Euler和以及推廣的Euler和的計算一直是人們關注的問題。在文獻［1］中，Borwein給出了如下結果：

之后，Philippe等人［2］利用留數定理考慮了更一般的Euler和

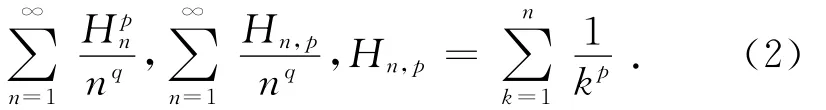
其中，整數p，q≥1，p＋q為奇數，然而對于下面交錯Euler和的計算卻比較困難。David Bailey利用PSLQ方法得到如下結果

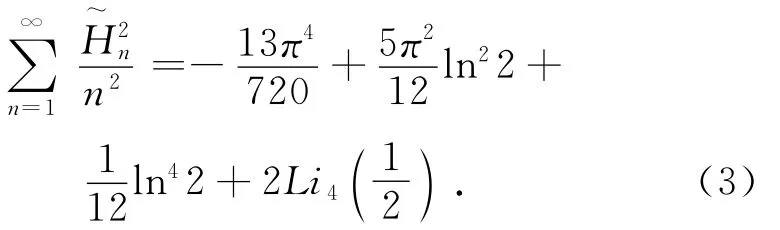
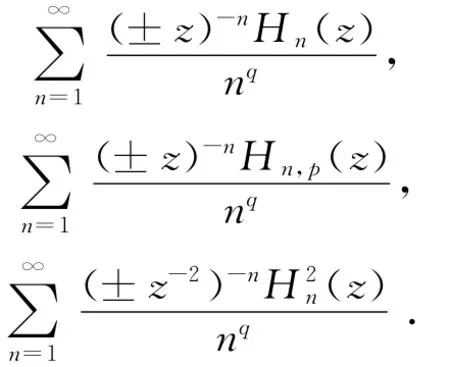
其中z是復平面單位圓上的復數。值得注意的是各種Euler和在量子力學中有著重要的應用，因此本文的研究無論從理論還是應用方面都是很有意義的。

1 主要定理

有關Euler和的計算，早些Euler采用的留數法仍然是最有效的方法之一，即下面的引理。

引理 （Cauchy，Lindel?f） 設ζ（s）是核函數，r（s）是有理函數且在無窮遠處具有O（s－2）.那么，

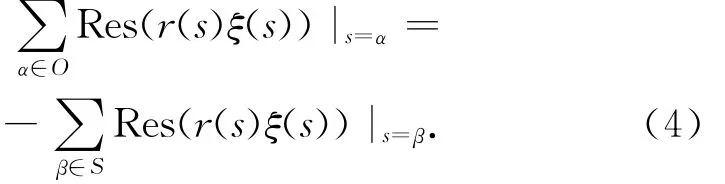
其中：S是r（s）的極點；O是ξ（s）的極點且不含有r（s）的極點；Res（h（s））｜s＝λ表示h（s）在s＝λ處的留數。

我們引入的核函數

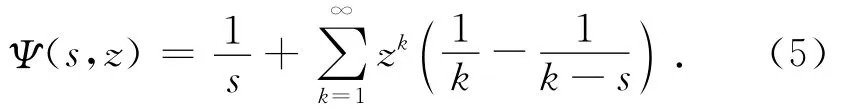
其中z是單位圓上的復數。Ψ（s，z）的極點是0，1，2，…，且在極點處的冪級數展開式

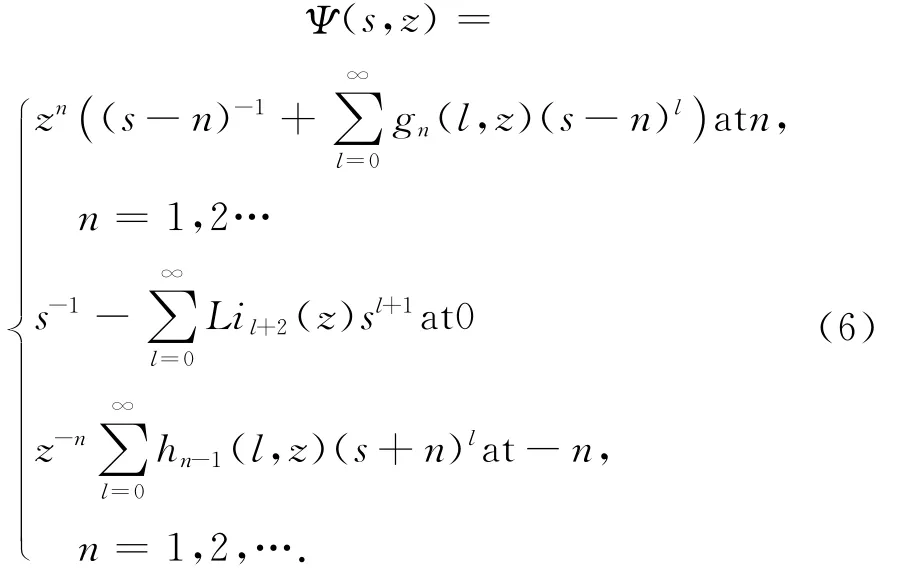
其中

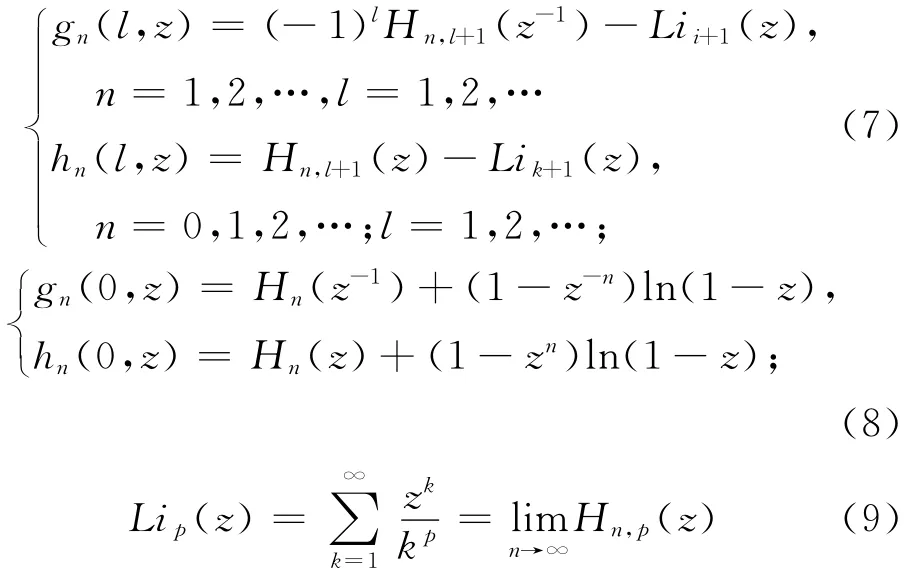
是多項式對數函數。由（6）我們可以得到

和

最后我們還需要下面的展開

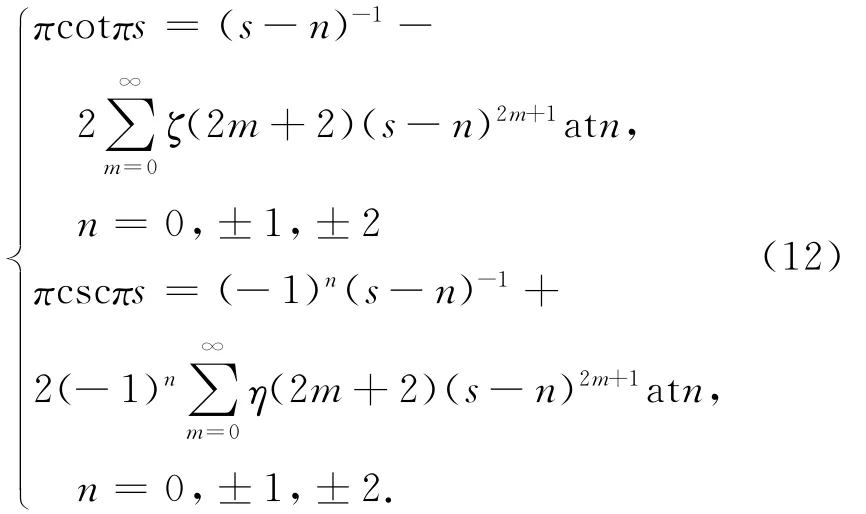
其中，ζ（n），η（n）＝ （1－21－n）ζ（n）分別是黎曼Zeta函數和η函數。

利用引理和（10）－（12）我們就得到了下面的兩個定理。

定理1 如果整數q≥2，那么

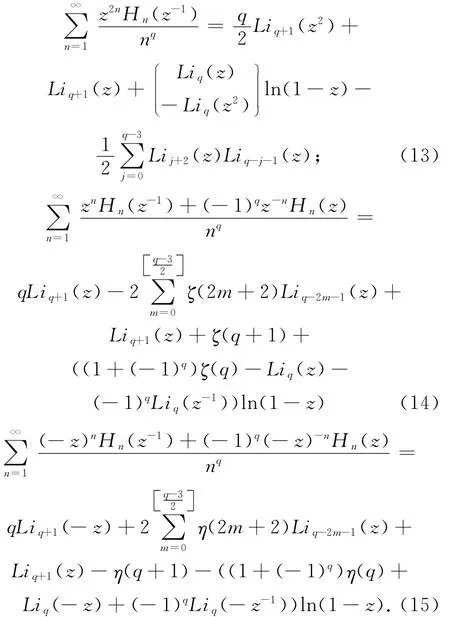
定理2 如果整數q≥2，p≥2，那么

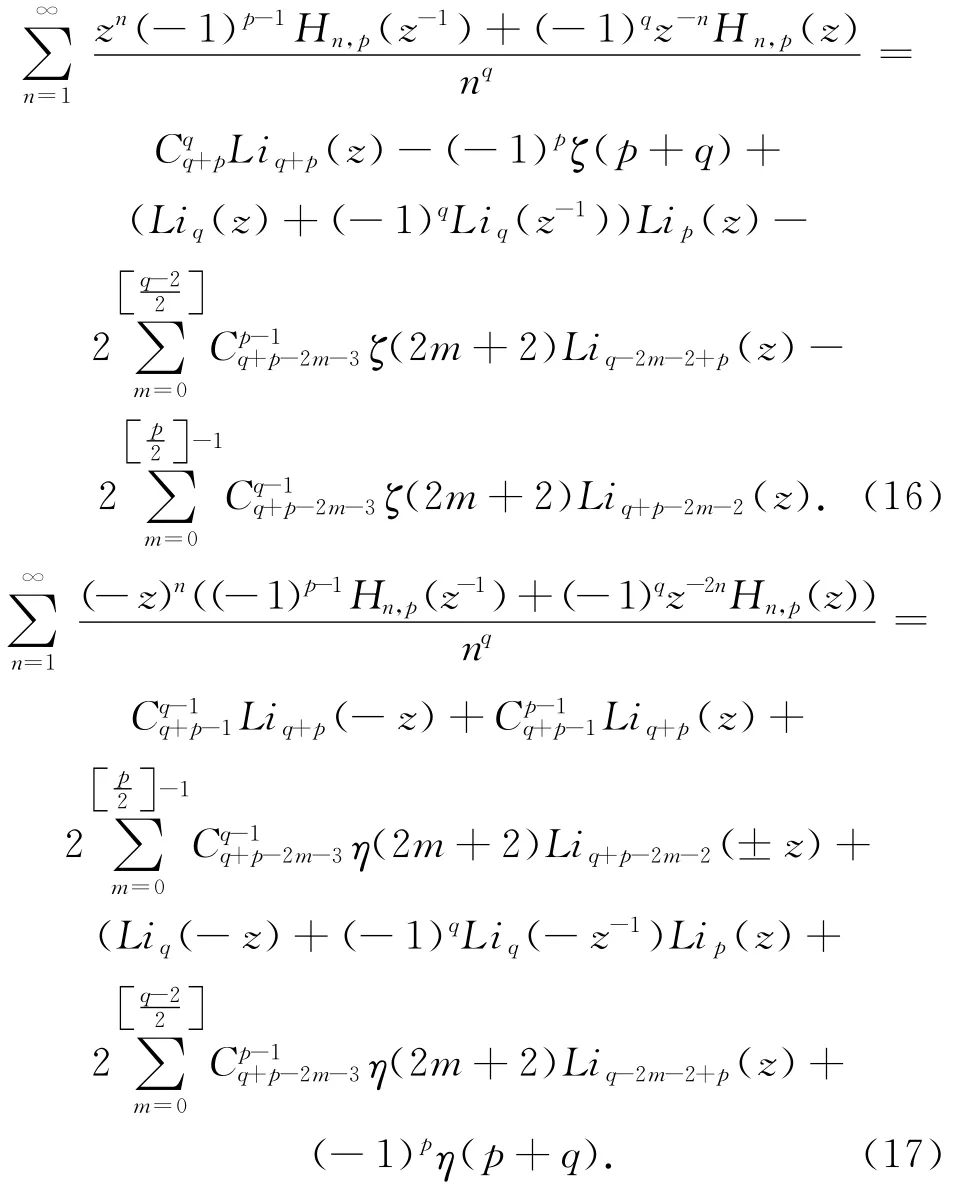
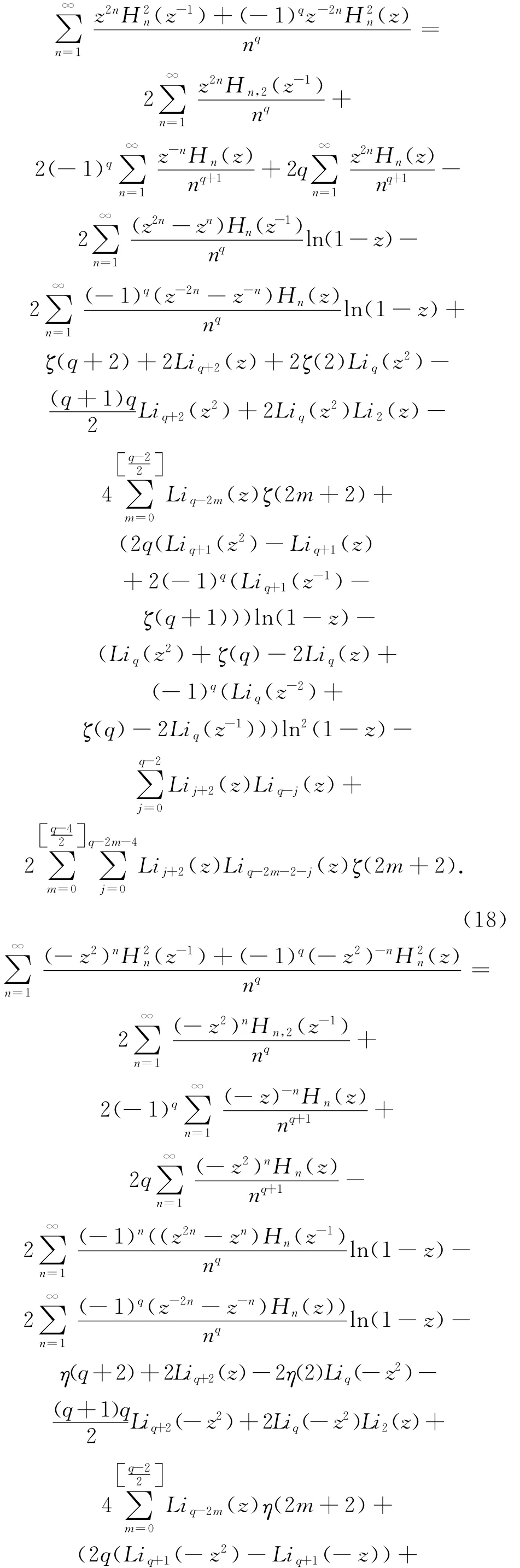
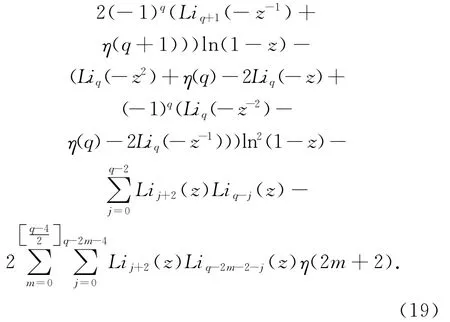
定理1，2的證明 這兩個定理證明的關鍵是留數的計算，因此我們只證明式（18），其它證明完全類似。簡單計算可知留數為

將式（7）和式（8）代入上式并利用引理可知（18）成立。

2 定理的應用

本文的特點是由于我們引進了含有參數的基本核函數式（5），把許多Euler和的計算問題統一起來討論，通過選取不同的參數z，得到各種擴展的Euler和。為了說明我們給出結果的有效性，討論一些特殊參數z對應的Euler和。讓式（13）—（19）中z＝1，就得到了通常Euler和的結果，這些結果可以見文獻［2，4］。不過我們將式（16）對應的結果寫出來

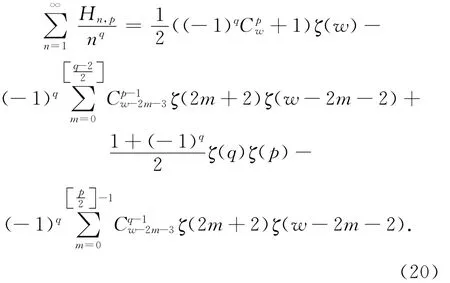
其中，w＝p＋q是奇數。由于（20）式的右邊都是黎曼Zeta函數的代數和，我們把它稱為第一閉形式。例如（1）就是閉形式。如果Euler和能用多項式對數函數Lin（z）和特殊常數表示，我們把它稱為第二閉形式。例如（3）和（13）都是第二閉形式。對于許多積分和Euler和人們希望得到這兩種閉形式，這也是目前人們研究的一個熱點。特別當z＝±1時，（13）就是第一閉形式，即

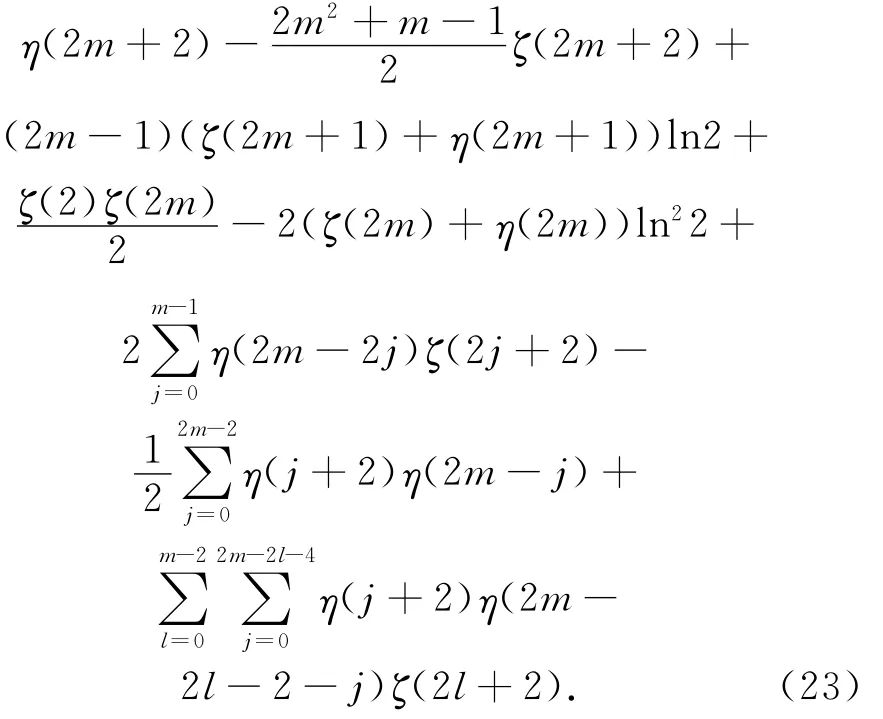
在式（14）中，讓z＝－1，我們有

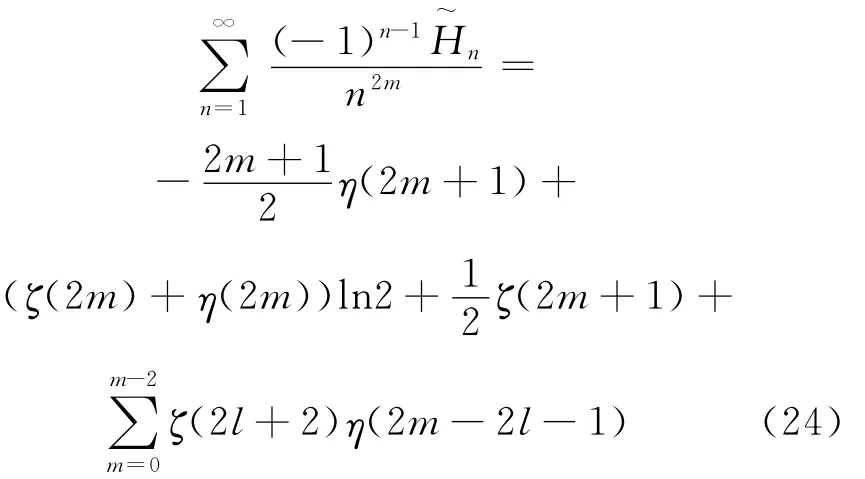
將式（21）和式（24）代入到式（22）和式（23）中，我們得到

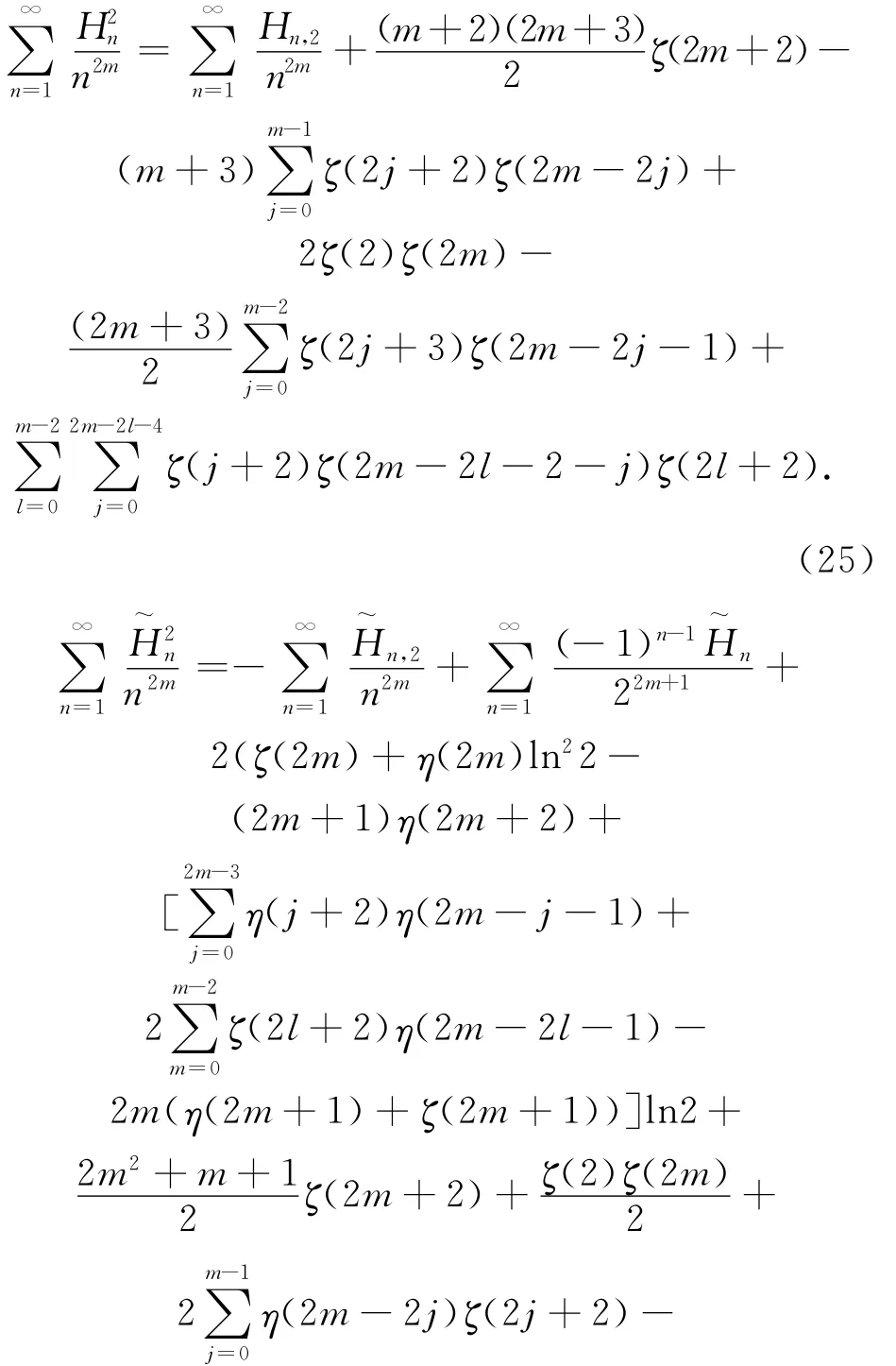
下面我們考慮一些新的Euler和，首先設整數P，Q是不可約的，那么

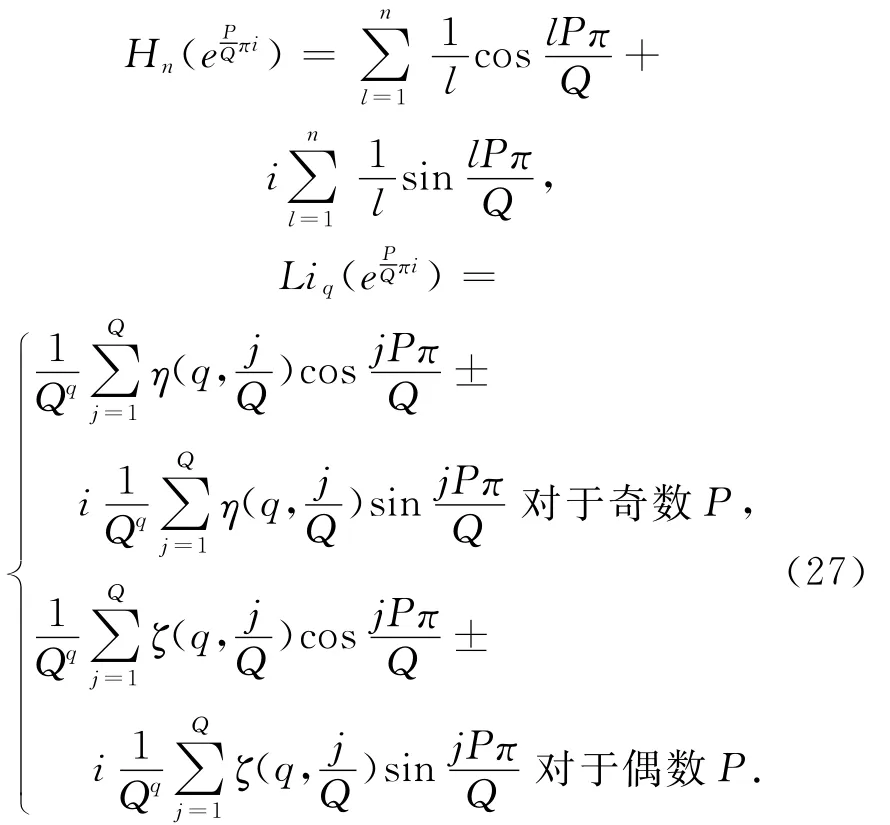
其中，ζ（q，a），η（q，a））是黎曼zeta函數和η函數的推廣，前者通常稱為Hurwitz Zeta函數，它們的定義是

在式（13）中讓z＝eQPπi（整數P，Q是不可約的），利用式（27）我們可以得到下面擴展Euler和的恒等式。

1）當P為偶數時，

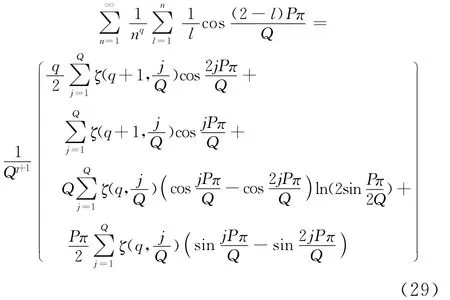
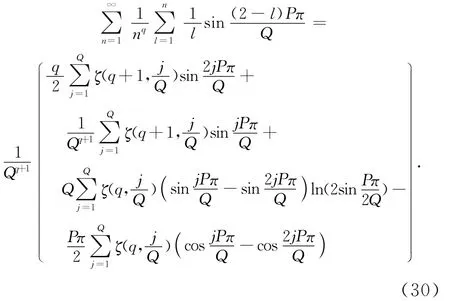
2）當P為奇數時，

完全類似地，從式（14）－式（19）也可以得到其他新的擴展Euler和的恒等式。因篇幅所限，不再舉例。

3 結論

通過引進含有參數的Euler和，將各種Euler和統一起來討論；通過適當選取參數可以得到許多新的Euler和。本文應用Cauchy和Linde?f定理仍然是解決Euler型和的重要手段之一，關鍵是核函數的構造。我們引進含有參數Z的基本函數Ψ（S，Z）是本文的另一創新點。由于合理地選取構造核函數的基本函數 ，因而解決了含有參數的線性和非線性Euler和的Zeta函數和Hurwitz Zeta函 數表示問題。

［1］ David Borwein，Jonathan M Borwein.On an Intriguing Integral and Some Series Related toζ（4）［J］.Proceedings of the A-merican Mathematical Society，1995，123（4）：1191-1198.

［2］ Philippe Flajolet，Bruno Salvy，Euler Sums and Contour Integral Representations［J］.Experimental Mathematics，1998，7（1）：15-35.

［3］ 商妮娜，秦惠增.一類擴展Euler和的表示問題［J］.純粹數學與應用數學，2011（6）：730-741.

［4］ David Borwein，Jonathan M Borwein，Roland Girgensohn.Explicit Evaluation of Euler Sums［J］.Proceedings of the Edinburgh Mathematical Society，1995，38，277-294.