綜合孔徑微波輻射計互耦模型與校正方法

郭 強 謝利子 馮小虎 林維夏 張志清 張 勇

(中國氣象局中國遙感衛星輻射測量和定標重點開放實驗室，國家衛星氣象中心，北京 100081)

引 言

微波輻射計可獲取大氣、海洋、陸地微波輻射圖像，反演降水、地表參數和水氣等參數，獲得大氣層不同高度的溫、濕度分布和卷云參數，并探測地表溫度和表面發射率。星載微波輻射計是氣象衛星的重要荷載之一，已在我國新一代極軌氣象衛星FY-3上裝載。在靜止軌道上裝載微波輻射計將大大提高獲取資料的時效性，為數值預報、模式計算和天氣分析提供有力的數據支持。我國已規劃發展三軸穩定的FY-4新一代靜止氣象衛星，用于接替現有的FY-2系列靜止氣象衛星。計劃發展光學和微波兩種類型的FY-4衛星，目前FY-4光學星已立項。

靜止軌道微波遙感的關鍵是需要高精度大口徑掃描天線，采用綜合孔徑天線的干涉式被動微波成像技術[1-2]可以有效減小天線口徑。干涉式綜合徑微波輻射計通過采用不同基線的干涉測量，得到合成一個等效大口徑天線所需的所有基線組合，對目標輻射亮溫的空間譜進行測量，并利用傅里葉變換反演得到目標亮溫分布。綜合孔徑微波輻射計實際上就是多個具有不同基線的二元干涉儀的組合。利用傅氏域的共軛對稱性，可以使天線物理孔徑減小一半，天線陣列大大稀疏。

對于綜合孔徑天線陣列，天線單元之間不可避免地存在相互耦合，這種互耦作用會改變天線單元方向圖，造成輻射效率損失，導致輻射計反演圖像的失真，使系統性能下降。現有的文獻[3-4]對綜合孔徑微波輻射計互耦做過一些研究分析，但這些工作并不是建立在天線理論分析的基礎上，只是將互耦關系用系數替代，不能清晰地描述互耦對微波輻射計影響的機理。若采用文獻[3]的分析對互耦作用進行校正，僅能通過測量方法得到包含復雜誤差影響的轉移矩陣，無法建立綜合孔徑微波輻射計受天線互耦影響的完整理論模型，也無法深入研究天線互耦對系統的影響及相應的反演誤差校正方法。從天線互耦機理出發，建立便于研究和分析的綜合孔徑微波輻射計互耦理論模型，討論消除互耦影響的反演校正方法，并給出通過優化天線匹配減小互耦影響的方法。

1.天線互耦

互耦是指天線陣元之間的電磁作用，一個陣元產生的電場會改變其他陣元上的電流分布以及輻射或接收方向圖。互耦會導致天線輸入端與饋線的阻抗不匹配，造成輻射效率的損失[5]。另一方面，天線間的互耦作用會導致各天線方向圖的不同，一定程度上降低信號的相關性。隨著天線陣元間距的增大，互耦會逐漸變小。對于一個雙偶極子線性天線陣，歸一化陣元間距為0.2時，利用NEC[6]仿真得到互耦影響下的單個天線遠場方向圖如圖1所示，另一偶極子天線終端接50 Ω負載。

(a) 有互耦

(b) 無互耦圖1 存在(a)和不存在(b)互耦的雙偶極子 天線中單個天線的輻射方向圖

考慮綜合孔徑微波輻射計上兩天線組成的二元干涉儀，采用網絡分析法將其等效為二端口網絡，則有電壓和電流關系

(1)

2.系統模型

根據前面對天線互耦的分析，利用阻抗矩陣來描述綜合孔徑微波輻射計的互耦效應，可以建立圖2所示的系統模型。采用M單元稀疏天線陣，ZRC為天線阻抗矩陣，ZL為負載阻抗矩陣。天線遠場區觀測區域S上的點x到天線陣元的距離為ρ(θ)，θ為對應的觀察角。

圖2 考慮天線互耦影響的綜合孔徑微波輻射計系統模型

根據基本電路理論，天線陣元接收電壓與負載端接收電壓的關系為

VR=ZL(ZRC+ZL)-1V=CRV

(2)

考慮微波輻射計的天線陣元i和j，在x坐標上的位置分別為xi和xj.根據綜合孔徑微波輻射計的原理，兩天線接收電壓Vi和Vj的復相關所代表的可見度函數與觀測目標的亮溫分布為傅里葉變換對關系。對于觀測區域在天線遠場區的情況，天線方向圖為F(θ)，觀測目標的輻射場強為E(θ)，則Vi可寫為[3]

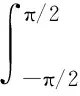
(3)

接收電壓Vi和Vj的復相關記為

[E(θ)?E(θ′)]·

e-j(2π/λ)[ρi(θ)-ρj(θ′)]dθdθ′

(4)

式中：符號?表示復相關；c為常數。對于遠場區，根據幾何關系近似有ρi-ρj≈(xi-xj)sinθ=dijsinθ，E(θ)?E(θ′)=c0T0(θ)δ(θ′-θ)，則上式可進一步簡化為

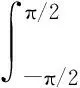
(5)

令l=dij/λ，T(θ)=c2c0F2(θ)T0(θ)cosθ，t=sinθ，對上式作變量代換有

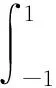
(6)

可見度函數Vc與亮溫分布T滿足傅里葉變換關系。設最小基線長度為Δl=lmin，基線l=nΔl，天線陣長度為L=NΔl，可以將式(6)寫成離散傅里葉變換形式

(7)

VRij=VRi?VRj

(8)

包含互耦影響的可見度函數可以寫成矩陣形式

VRc=CAVc+CB=CAWT+CB

(9)

式中：W=[e-j[2π/(2N+1)]kn](2N+1)×(2N+1)且WW*=(2N+1)I2N+1，I為單位矩陣，上標*表示復共軛；向量Vc為

Vc= [Vc[-N]Vc[-N+1] …Vc[0]

…Vc[N-1]Vc[N]]

(10)

CA和CB可以根據基線組合情況結合式(8)得到，矩陣CA的元素由式(8)的前半部分決定，代表耦合關系；向量CB的元素由式(8)的后半部分決定，代表接收信號自相關的影響。當不存在互耦影響時CA為對角陣且CB=0.以如圖3所示的稀疏天線陣結構為例，最小基線長度為D，共有6種基線組合，N=6.

圖3 稀疏天線陣

根據式(8)有

VRc[0] =VR11=VR1?VR1

VRc[1] =VR12=VR1?VR2

VRc[2] =VR34=VR3?VR4

……

VRc[6] =VR14=VR1?VR4

(11)

式中：VRc[-N]=(VRc[N])*.Vkk為常數，上面各式的后半部分即向量CB的元素為常數，有

(12)

Vkl與Vc[N]的關系為Vkl=Vc[M[k，l]]， 其中矩陣M為

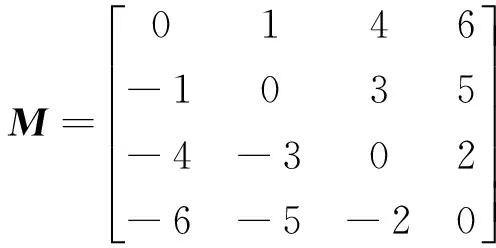
(13)

代表基線組合情況。根據式(11)，同樣可以將矩陣CA寫為矩陣形式。

3.反演校正

通過傅里葉反變換，可以反演得到亮溫分布

(13)

那么，互耦影響下反演亮溫與原始亮溫的關系寫成矩陣形式有

=CDT+CE

(14)

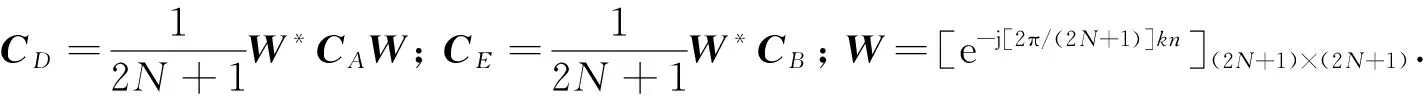
根據式(9)和式(14)，通過綜合孔徑微波輻射計天線陣特征參數和陣列分布求出耦合矩陣CR，得到CA和CB，進而得到系數矩陣CD和CE，就可以對互耦引起的反演亮溫失真進行校正，即有

(15)

通過仿真或測量可以得到天線自阻抗和互阻抗，用于本文給出的綜合孔徑微波輻射計互耦模型，便于進一步研究和分析。與簡單將互耦影響等效成可見度函數相關系數的方法相比，應用這種模型可以將綜合孔徑微波輻射計天線互耦的機理和校正方法清晰地表達出來，以便研究相應的方法來改善互耦造成的反演誤差。

為減小互耦作用，采用改善匹配網絡的方法來減小綜合孔徑天線單元間的耦合。研究表明：選擇適當的天線匹配網絡可以在一定程度上減小互耦造成的影響，改善多天線系統的性能[7-9]。自阻抗匹配是指天線端口與其自阻抗共扼匹配的情況。輸入阻抗匹配是指各天線終端的匹配負載阻抗等于其輸入阻抗的復共軛。天線的輸入阻抗由自阻抗和互阻抗共同決定，存在互耦時天線的輸入阻抗會隨天線間距大小而變化。多端口共軛匹配對于改善互耦影響和最大化信號能量傳輸而言是最優的匹配方案，但實現較為困難。采用包含互耦因素的輸入阻抗匹配或多端口網絡匹配優化天線匹配，可以改善綜合孔徑微波輻射計的性能，使耦合矩陣CR更接近于對角陣，其物理意義是天線互耦影響的減小。

4.仿真實驗

考慮圖3所示的稀疏天線陣結構，通過設定已知亮溫的觀測場景來驗證綜合孔徑微波輻射計天線互耦模型。為簡化分析，假設天線陣元為半波偶極子天線，天線單元的半徑為0.01λ，最小基線長度D=λ/2，天線陣長度L=6D，N=6，天線角分辨率為arcsin(2/N)=19.47°，不考慮輻射計靈敏度。天線的自阻抗和互阻抗根據文獻[10]中的感應電動勢法求取。觀測場景的背景亮溫為Tb=40 K，在輻射計視場中心和左側40°處分別有亮溫為TA=100 K和TB=80 K的點目標源A和B.

根據本文建立的綜合孔徑微波輻射計互耦模型進行仿真，得到在自阻抗匹配和輸入阻抗匹配情況下包含互耦影響的相對亮溫分布，以及采用本文的反演校正方法對互耦進行校正得到的原始亮溫分布。以100 K作為標準參考值，得到的相對亮溫分布曲線如圖4所示，對應的輻射亮溫圖像見圖5.

圖4 相對亮溫分布

圖5 輻射亮溫圖像

5.結 論

近年來，我國在綜合孔徑微波輻射成像技術方面的研究取得了顯著成果，一些技術已經達到國際前沿水平。星載綜合孔徑微波輻射計關鍵技術的研究，是下一代FY-4靜止氣象衛星發展計劃的重要部分。針對綜合孔徑微波輻射計天線陣單元間的互耦問題，利用阻抗參數方法描述天線間的互耦作用，建立了清晰完整的綜合孔徑微波輻射計互耦模型。通過對綜合孔徑微波輻射計亮溫反演原理的描述，給出互耦模型下反演亮溫失真的理論分析，并提出相應的校正方法。通過對比不同天線匹配網絡的情況，討論了如何改善互耦引起的亮溫反演失真。這些工作對于研究和解決綜合孔徑微波輻射計的反演誤差，提供了有益的思路。

[1] THOMPSON A R. Interferometry and Synthesis in Radio Astronomy[M]. New York: John Wiley & Sons, 2nd edition, 2001.

[2] RUF C S, SWIFT C T, TANNER A B, et al. Interferometric synthetic aperture microwave radiometry for the remote sensing of the earth[J]. IEEE Trans. Geosci. Remote Sensing, 1998, 26(5): 597-611.

[3] 董曉龍，張升偉，吳 季，等. 綜合孔徑微波輻射計天線單元互耦的影響及其校正[J]. 電子學報. 2001, 29(9): 1280-1282.

DONG Xiaolong, ZHANG Shengwei, WU Ji, et al. Effect of mutual coupling between antenna elements on the imaging of synthetic aperture radiometer and its calibration[J]. Chinese Journal of Electronics, 2001, 29(9): 1280-1282.

[4] 董曉龍，吳 季，姜景山. 信道互耦和不平衡度對綜合孔徑微波輻射計復相關干涉測量的影響分析及其校準[J]. 電子學報. 2001, 29(7): 947-949.

DONG Xiaolong, WU Ji, JIANG Jingshan. Analysis and calibration of effects on complex correlations from mutual coupling and imbalance between channels[J]. Chinese Journal of Electronics, 2001, 29(7): 947-949.

[5] 李 忻, 聶在平. 天線互耦對MIMO無線信道性能的影響[J]. 電波科學學報, 2005, 20(4): 546-551.

LI Xin, NIE Zaiping . Effect of mutual coupling on the performance of MIMO wireless channels[J]. Chinese Journal of Radio Science, 2005, 20(4): 546-551.

[6] Numerical Electromagnetics Code (NEC)[CP]. http://www.nec2.org.

[7] WALLACE J W and JENSEN M A. Termination-dependent diversity performance of coupled antennas: network theory analysis[J]. IEEE Trans. Antennas and Propagation, 2004, 52: 98-105.

[8] GUO Qiang, ZHOU Xilang, YIN Wenyan, et al. Effects of antenna matching on compact MIMO beamforming systems in frequency-selective fading channels[C]//Asia Pacific Microwave Conf., Dec. 2009, 1: 445-448.

[9] 郭 強，周希朗，張維炯. 天線匹配對萊斯信道下緊湊MIMO系統性能的影響[J]. 電波科學學報. 2009, 24(6): 1009-1013.

GUO Qiang, ZHOU Xilang, ZHANG Weijiong. Effect of antenna matching on compact MIMO system performance in Rician fading channels[J]. Chinese Journal of Radio Science, 2009, 24(6): 1009-1013.

[10]BALANIS C A. Antenna Theory Analysis and Design[M]. New York: John Wiley & Sons, 2nd edition, 1997.