基于傳聲器陣列的產品噪聲源定位技術的應用

李嘉，張國慶

（深圳市計量質量檢測研究院，廣東 深圳 518055）

0 引言

傳聲器陣列定位技術是一種非常有效的噪聲源識別、定位以及聲場可視化的工具。它可在非接觸條件下對噪聲源進行精確的定位，在機電產品工作噪聲改善，汽車、飛機、高鐵的噪聲、振動與舒適性（NVH）檢測，大型旋轉機械的非接觸式在線故障診斷等領域有著廣泛的應用[1]。

傳聲器陣列是指由一定的幾何結構排列而成的、若干個傳聲器組成的陣列，它具有很強的空間選擇性，而且不需移動傳聲器就可獲取移動的聲源信號，同時它還可以在一定的范圍內實現聲源的自適應檢測、定位及跟蹤，這使得它在諸多領域有著廣泛的應用[2]。傳聲器陣列聲源定位是指用傳聲器陣列來拾取聲音信號，通過對多路聲音信號進行分析與處理，在空間域中定出一個或多個聲源的平面或空間坐標，即得到聲源的位置。現階段，比較成熟并在測量領域應用較多的兩種聲源定位技術是：基于空間聲場變換法（STSF）的傳聲器陣列聲源定位技術和基于波束形成法（Beamforming）的傳聲器陣列聲源定位技術。

1 基于STSF的傳聲器陣列聲源定位技術

1.1 穩態STSF定位方法

在近場測量時，廣泛使用的方法為空間聲場變換法（STSF： Spatial Transformation of Sound Field）。

由理想流體媒質中的小振幅聲波的波動方程[3-4]，可以得到無時間變量的穩態聲場的Helmholtz方程：

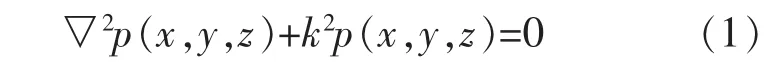
式（1）中：p（x，y，z）——空間聲壓，是直角坐標系 x，y，z的函數；

k=w/c=2π/f——聲波數；

c——聲速；

λ——特征波長。

對于z＞0的空間為自由聲場的情況，即所有的聲源均位于z=0平面以下，用格林公式求解式（1），得z＞0空間任一點的聲壓為：

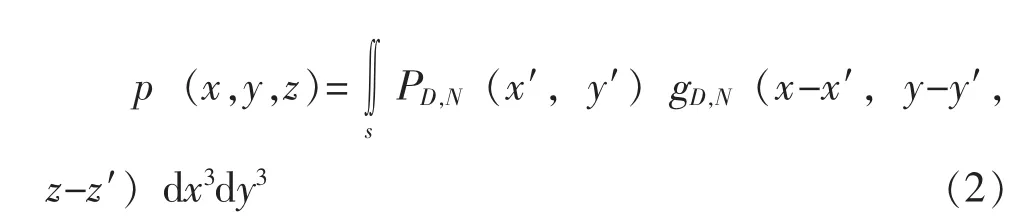
式（2）中，S積分在無窮大的邊界面進行，gD，N為無窮大平面的格林函數。

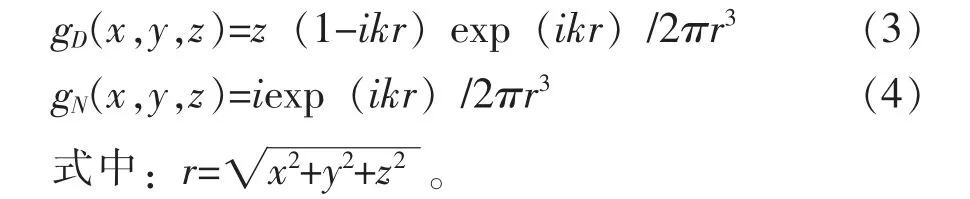
已知空間內沿x，y方向上的二維連續傅里葉變換:

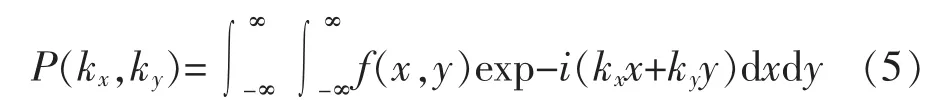
對式（2）兩邊進行二維傅里葉變換，根據二元卷積定理可知：

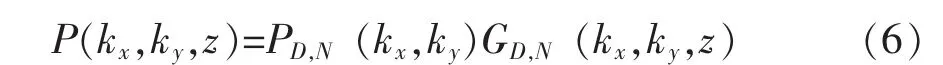
式（6） 中： P（kx，ky，z）， PD，N（kx，ky）是聲壓 p（x，y，z）和邊界條件 PD，N（x，y）的二維連續傅里葉變換；

GD，N（kx，ky，z）為 gD，N的二維傅里葉變換， 解析表達式為：

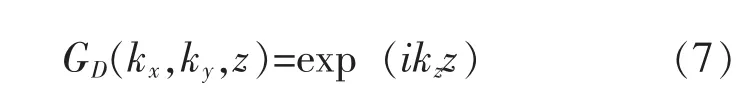
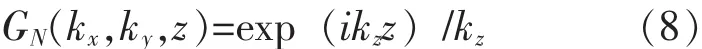
將式（7）、（8）帶入式（6），可以建立任意兩平面z=zH（全息面）和z=zS（重建面）的一般關系[5]：

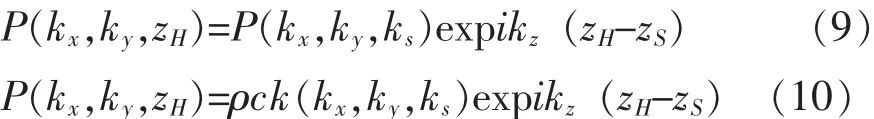
式中：ρ——聲介質的平均密度。

由式（9）、（10）可知：已知 z=zS平面的聲壓或質點法向振速，可以預測出z=zH的聲壓情況，通過Euler公式可以很方便地推測出z=zH面的質點法向振速，由此，可以進一步地導出聲場參量：聲強及遠場指向性等；同理，已知z=zH的聲壓數據也可以反演表面z=zS的聲壓和質點法向振速。由此，可以得到平面近場聲全息的基本重建公式：

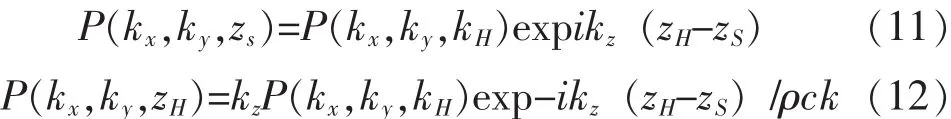
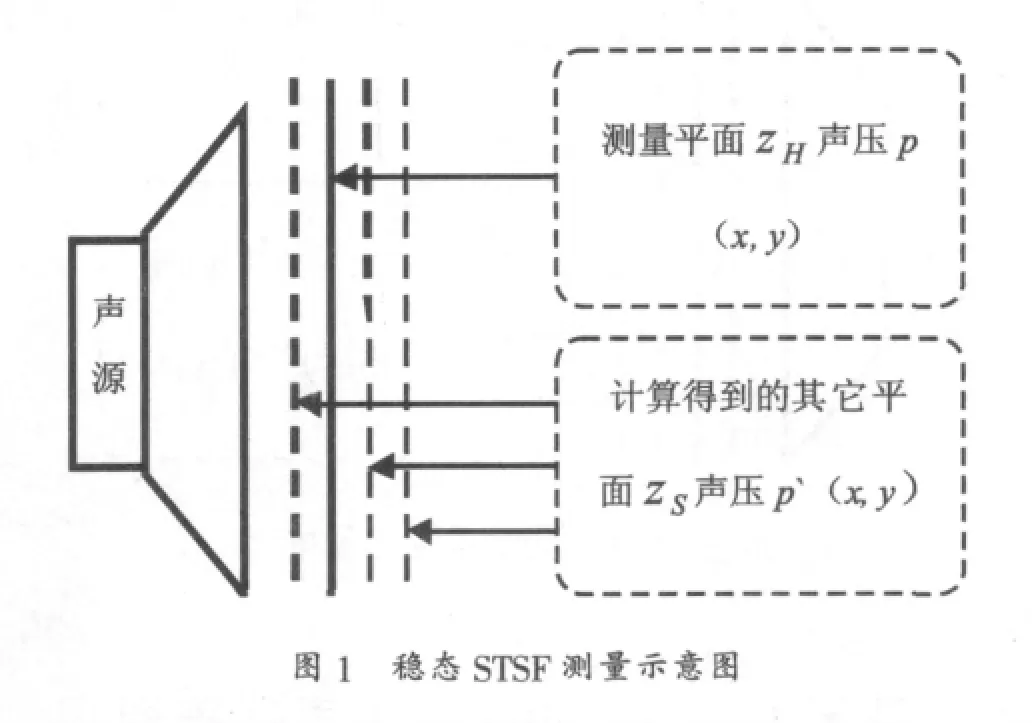
在實際的測量過程中，STSF測量系統通過將傳聲器陣列測得的一個平面的二維空間數據，通過近場聲全息（NAH：Near-field Acoustical Holography）和Helmholtz積分方程，計算出其它平面位置的聲壓，得到三維空間的聲場圖形，從而實現空間聲源定位，如圖1所示。

使用STSF技術的陣列聲學定位系統，要求傳聲器陣列必須覆蓋所測量的聲源表面，并且傳聲器陣列需要在被測聲源的近場測量。傳聲器在陣列中的間距決定了測量的上限頻率，如式（13）所示。

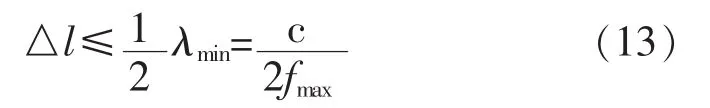
式（13）中：△l——傳聲器間距。

根據此規律，傳聲器間距和測量頻率的上限關聯典型值如表1所示。

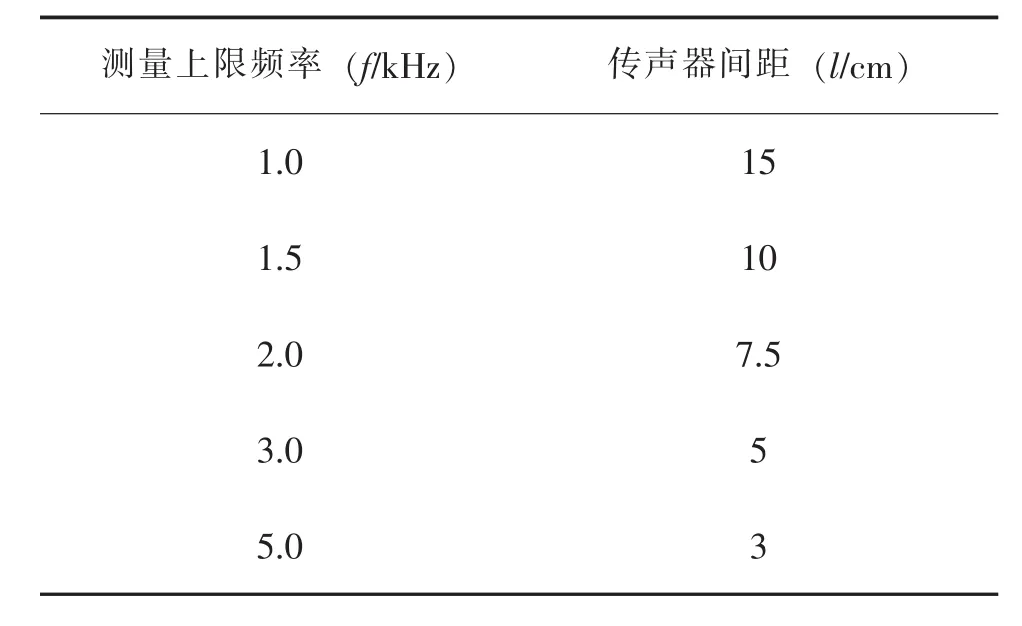
表1 STSF測量陣列聲器間距和測量頻率的上限關聯典型值

因此，使用STSF測量陣列進行聲源測量時，由于傳聲器陣列中測點間距的關系，測量頻率上限是有限的，通常在1.5kHz以下。

1.2 非穩態STSF定位方法

圖1所示的STSF測量系統，主要適用于穩態聲源的測量。當被測聲源為非穩態聲源時，需要在傅里葉變換和全息過程中加入時間參量t，其變換過程如圖2所示。

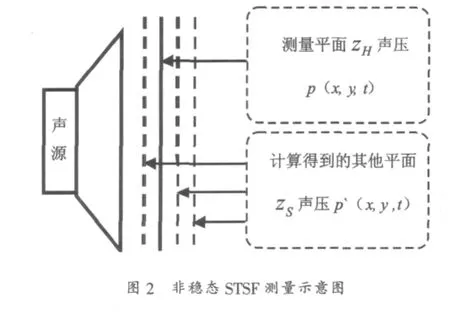
2 基于Beamforming的傳聲器陣列聲源定位技術

STSF測量方法解決了近場聲定位的測量，但是當測量遠距離聲源，或者聲源表面積很大，不可能使用傳聲器陣列在近場完全覆蓋時，就需要另一種可以使用較少測量點的傳聲器陣列，在較遠的距離對聲源進行定位測量的方法。最常見的就是基于Beamforming技術的聲源定位方法。

在使用STSF進行聲源定位時，由于是近場測量，可以認為聲源輻射方向與傳聲器陣列面垂直陣列中的每個傳聲器所接收到的信號之間在時間上是同步的；而在遠場測量時，聲源更接近于點聲源，如圖3所示。

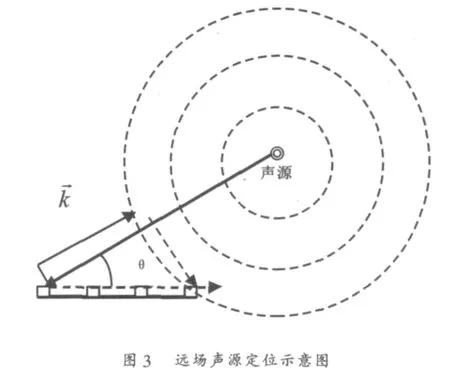
由于聲源和各個傳聲器之間的距離不相等，每個傳聲器接收到的聲波有不同的時延△m，式（14）表示了第i個傳聲器接收到的信號[6]。

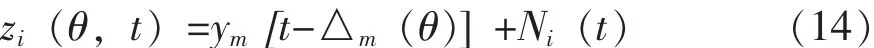
式（14）中：Ni（t）——表示均值趨于零的干擾。

由于傳聲器陣列的結構和聲速是已知的，于是，對于空間每個位置的聲源，都可以解出一組對應的時延。如果對每個傳聲器接收到的信號分別用△m修正，就要將來自聲源的聲波對齊，然后將所有M個修正后的信號求和；由于干擾信號Ni（t）的均值趨于零，因此，可以得到增強了的聲波信號， 見式（15）。

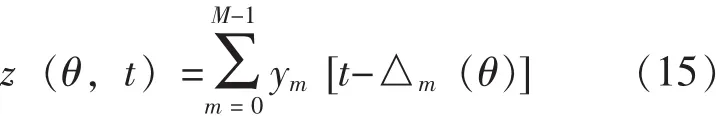
將圖3中的時延△m的向量形式帶入式（15），可得到接收信號的時域向量表達式，見式（16）。

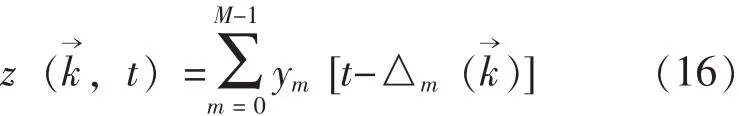
對式（16）進行傅里葉變換，即可求出接收信號的頻域向量表達式，見式（17）。

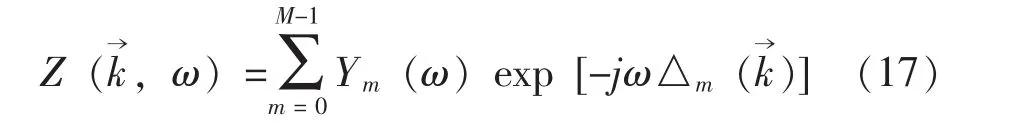
在使用時，Beamforming陣列聲學測試系統的測試距離最小值要求大于傳聲器矩陣的直徑，最大值可到無窮遠。其有效的聚焦范圍通常為測試距離的1.15倍，如圖4所示。系統的空間分辨率R≌（L/D）λ，測量上限頻率由fmax最大旁瓣量決定，下限頻率fmax＞3c/D。因此，Beamforming陣列聲學測試系統的測量下限頻率無法做到很低。

3 兩種噪聲源定位技術的應用條件

由于兩種聲源定位技術的原理有所不同，所以其適用的頻率范圍和空間范圍也各不相同。表2列出了兩種聲源定位技術在指標上的差異。

表2 STSF和Beamforming的對比

可以看出，STSF和Beamforming這兩種聲源定位技術，一個適用于近場中低頻，另一個適用于遠場中高頻，兩者互為補充。

4 結束語

在電子及工業產品的噪聲測量及改善的過程中，噪聲源的準確定位極為重要。為了保證聲源定位的準確性，應對不同的聲源特性合理地選擇傳聲器陣列聲源定位的方法，并結合信號頻譜分析、模態分析等技術，分析噪聲產生的原因，加以改善。同時，如何將兩種聲源定位技術的優點結合起來，實現一個傳聲器陣列可同時覆蓋近聲場和遠聲場，并可在全頻段進行聲源的定位測量，是聲源定位技術下一步研究的重點。

[1]李加慶，陳進，史重九.基于聲全息的故障診斷方法[J].機械工程學報，2009，45（5）:34-38.

[2]林志彬，徐柏齡.基于傳聲器陣列的聲源定位 [J].電聲技術， 2004， 5： 19-23.

[3]WILLIAMS E G， MAYNARD J D.Holographic imaging without the wavelength resolution limit[J].Physics Review Letters， 1980， 45： 554-557.

[4]WANG Z， WU S F.Helmholtz equation-least-squares method for the reconstructing the acoustic pressure field[J].Journal of the Acoustical Society of America， 1997， 102：2020-2032.

[5]宮延明，金濤，謝志東.應用近場聲全息方法對噪聲源的實驗研究 [J].現代機械，2008，（3）:34-37.

[6]錢世鍔.聲學照相機 [J].國外電子測量技術，2009，28（2）： 5-8.