基于支持向量機(jī)的MEMS陀螺儀隨機(jī)漂移補(bǔ)償*

李澤民，段鳳陽，馬佳智

(空軍航空大學(xué)航空控制工程系，長春130022)

隨著微電子技術(shù)和集成電路技術(shù)的發(fā)展，采用微機(jī)電系統(tǒng)(MEMS)技術(shù)的慣性傳感器以其體積小、質(zhì)量輕、成本低、產(chǎn)品可靠性高等優(yōu)異特性，被廣泛應(yīng)用于汽車、航空、航天和武器制導(dǎo)等軍民領(lǐng)域[1]。由于受自身結(jié)構(gòu)缺陷和加工工藝的限制，MEMS陀螺儀存在較大的漂移，尤其是其中的隨機(jī)漂移，具有隨機(jī)性、非線性、非平穩(wěn)和弱時(shí)變特性，已成為制約MEMS陀螺儀向高精度領(lǐng)域應(yīng)用的主要因素，必須建立有效的誤差模型對(duì)其進(jìn)行預(yù)測(cè)和補(bǔ)償[2]。

目前常用的陀螺儀隨機(jī)漂移預(yù)測(cè)方法主要有兩類:一類是以傳統(tǒng)時(shí)間序列分析法為代表的統(tǒng)計(jì)建模方法，如將AR模型或者ARMA模型與Kalman濾波器相結(jié)合[3－4]。這類方法要求時(shí)間序列具有平穩(wěn)性、正態(tài)性和獨(dú)立性特征，極大的限制了模型的使用范圍和預(yù)測(cè)精度。另一類是以神經(jīng)網(wǎng)絡(luò)為代表的人工智能算法[5]。神經(jīng)網(wǎng)絡(luò)具有很好的非線性逼近能力，但神經(jīng)網(wǎng)絡(luò)訓(xùn)練過程遵循的是經(jīng)驗(yàn)風(fēng)險(xiǎn)最小化準(zhǔn)則，存在著過擬合現(xiàn)象，導(dǎo)致算法的泛化性能差，并且訓(xùn)練過程受局部極小點(diǎn)的困擾。基于統(tǒng)計(jì)學(xué)習(xí)理論[6]的支持向量機(jī)SVM(Support Vector Machine)方法，其訓(xùn)練過程遵循的是結(jié)構(gòu)風(fēng)險(xiǎn)最小化原則，不易發(fā)生局部最優(yōu)及過擬合現(xiàn)象，能夠很好的克服神經(jīng)網(wǎng)絡(luò)的上述缺陷，非常適合非線性的隨機(jī)序列動(dòng)態(tài)建模[7]。

本文通過對(duì)隨機(jī)漂移序列進(jìn)行相空間重構(gòu)，將回歸支持向量機(jī)用于陀螺儀隨機(jī)漂移的預(yù)測(cè)和補(bǔ)償，以探索新的更加有效的隨機(jī)漂移補(bǔ)償方法。

1 支持向量機(jī)預(yù)測(cè)模型

支持向量機(jī)是建立在統(tǒng)計(jì)學(xué)習(xí)理論的VC維理論和結(jié)構(gòu)風(fēng)險(xiǎn)最小化準(zhǔn)則的基礎(chǔ)上，根據(jù)有限樣本信息在模型的復(fù)雜度和學(xué)習(xí)能力之間尋求最佳折衷，以期望獲得最好的泛化能力[8]。其基本思想是對(duì)于非線性問題，利用非線性變換將其映射到一個(gè)高維的特征空間中，并在此空間進(jìn)行線性分析，即將低維空間的非線性問題轉(zhuǎn)化為高維特征空間中的線性問題來解決。通常引入一個(gè)核函數(shù)以代替高維空間中的內(nèi)積運(yùn)算，從而巧妙的避免了復(fù)雜的計(jì)算，并且有效地克服了維數(shù)災(zāi)難和局部極值問題。

對(duì)于給定的容量為N的隨機(jī)漂移樣本集T={xk，yk}(k=1，2，…，N;xk∈Rn，yk∈R)，其中 xk為輸入變量，yk為相應(yīng)的目標(biāo)值。根據(jù)支持向量機(jī)的基本思想，首先通過非線性變換將輸入空間映射到一個(gè)高維特征空間，在此特征空間中的SVM預(yù)測(cè)模型為:

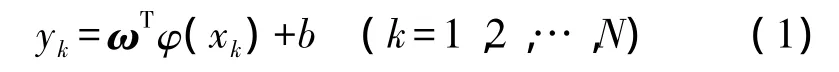
式中，ω、b和φ(xk)分別為權(quán)值向量、閾值和進(jìn)行空間映射的非線性變換。依據(jù)結(jié)構(gòu)最小化準(zhǔn)則，并考慮偏離點(diǎn)的影響，引入非負(fù)的松弛因子，問題轉(zhuǎn)變?yōu)橛屑s束最優(yōu)問題:

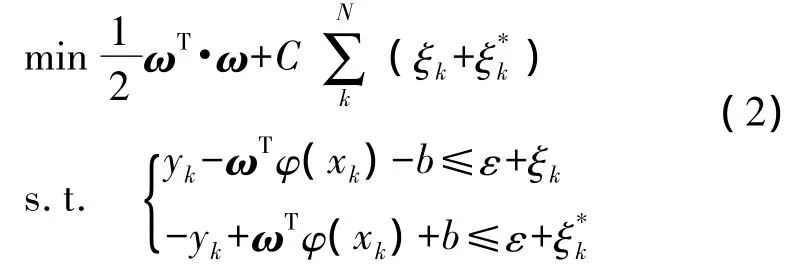
對(duì)于此約束二次規(guī)劃問題，依據(jù)KKT條件，通過引入非負(fù)的拉格朗日乘子α，α*，將問題轉(zhuǎn)化為二次規(guī)劃的對(duì)偶問題:

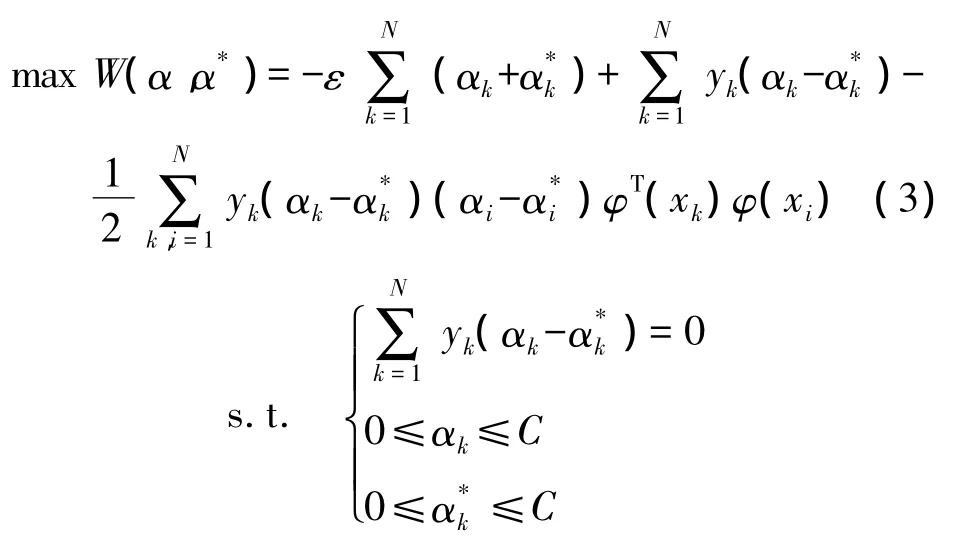
求解上式可得到所求的預(yù)測(cè)模型:

上式需要計(jì)算高維空間的內(nèi)積，當(dāng)維數(shù)很高時(shí)計(jì)算量巨大，造成所謂的維數(shù)災(zāi)難。引入核函數(shù)K(xk，x)來代替內(nèi)積的計(jì)算，即

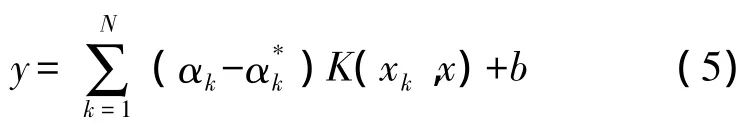
核函數(shù)接受低維的輸入而計(jì)算高維的內(nèi)積，可以有效的避免維數(shù)災(zāi)難。根據(jù)泛函理論，滿足Mercer條件的函數(shù)都可以作為核函數(shù)。很多研究和實(shí)驗(yàn)表明:當(dāng)缺少過程的先驗(yàn)知識(shí)情況下，選擇徑向基核函數(shù)比選擇其他核函數(shù)預(yù)測(cè)性能好。在對(duì)各種常用核函數(shù)預(yù)測(cè)效果對(duì)比的基礎(chǔ)上，本文選擇了徑向基核函數(shù) K(x，xi)=exp(－‖x－xi‖2/σ2)。

2 支持向量機(jī)預(yù)測(cè)模型的建立

2.1 相空間重構(gòu)

陀螺的隨機(jī)漂移是一維的標(biāo)量時(shí)間序列，需要通過相空間重構(gòu)，把標(biāo)量時(shí)間序列嵌入到一個(gè)輔助的相空間中，以得到滿足支持向量機(jī)要求的訓(xùn)練和測(cè)試序列。

由Takens嵌入定理[9]可知:如果嵌入維的維數(shù)m≥2D2+1，D2是系統(tǒng)的維數(shù)，則通過相空間重構(gòu)的得到的系統(tǒng)與原始系統(tǒng)是等價(jià)的。對(duì)于標(biāo)量時(shí)間序列:{x(i)}，i=1，2，…N，由延遲坐標(biāo)相空間重構(gòu)法得到的重構(gòu)序列為:

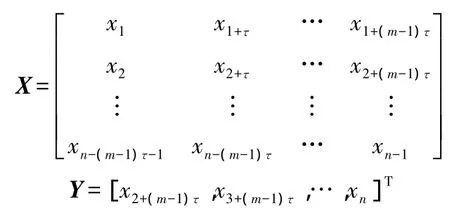
其中m和τ分別為嵌入維數(shù)和延遲時(shí)間，對(duì)一個(gè)序列進(jìn)行相空間重構(gòu)關(guān)鍵是要確定這兩個(gè)參數(shù)。嵌入維數(shù)m表征吸引子的空間間隔和幾何不變量;延遲時(shí)間τ反映了任意兩個(gè)相鄰延遲坐標(biāo)點(diǎn)的相關(guān)程度。m和τ的不恰當(dāng)配對(duì)將影響重構(gòu)后的相空間結(jié)構(gòu)與原空間的等價(jià)關(guān)系。本文使用的C-C法是通過引入嵌入窗寬τw=(m－1)τ將m和τ統(tǒng)一起來的。C-C法基于大量的統(tǒng)計(jì)結(jié)果產(chǎn)生，計(jì)算量少、計(jì)算速度快，計(jì)算結(jié)果理想，并且魯棒性能和抗噪聲性能尤其突出，是最為廣泛使用的計(jì)算時(shí)間窗的方法。

2.2 核函數(shù)參數(shù)和SVM參數(shù)的選擇

支持向量機(jī)模型中，待確定的參數(shù)為不敏感系數(shù)ε、懲罰系數(shù)C和徑向基核函數(shù)中的參數(shù)σ，這幾個(gè)參數(shù)在模型的訓(xùn)練過程中都是定值，需要訓(xùn)練前事先確定。常用的方法有交叉驗(yàn)證法、基于VC維的誤差估計(jì)和LOO誤差估計(jì)[10－11]。本文使用的k-折交叉驗(yàn)證法，對(duì)于中等規(guī)模的問題而言，是最為可靠的參數(shù)選擇方式。

統(tǒng)計(jì)學(xué)習(xí)理論中，通過比較算法的泛化能力來評(píng)價(jià)支持向量機(jī)的好壞，即檢驗(yàn)?zāi)Ｐ蛯?duì)測(cè)試集的預(yù)測(cè)精度來衡量該模型的優(yōu)劣。本文使用的誤差指標(biāo)為均方根誤差:

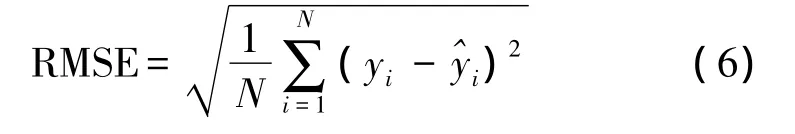
即所有格點(diǎn)中，均方根誤差最小的格點(diǎn)處對(duì)應(yīng)的參數(shù)為所尋找的最優(yōu)參數(shù)組合。

3 支持向量機(jī)預(yù)測(cè)模型的實(shí)驗(yàn)驗(yàn)證

3.1 實(shí)驗(yàn)方法和步驟

采集一組MEMS陀螺儀STIM202的靜態(tài)數(shù)據(jù)，經(jīng)過確定性誤差補(bǔ)償和小波閾值去噪，得到表征陀螺儀隨機(jī)漂移的時(shí)間序列。當(dāng)樣本容量大于3 000時(shí)，C-C法尋找最優(yōu)相空間重構(gòu)參數(shù)的效果較好，因此取該時(shí)間序列中長度為3 500的一段序列作為實(shí)驗(yàn)數(shù)據(jù)。以前500個(gè)樣本點(diǎn)為訓(xùn)練集訓(xùn)練模型，用后2 000個(gè)樣本點(diǎn)做測(cè)試。實(shí)驗(yàn)步驟如下:

(1)相空間重構(gòu)

首先對(duì)此標(biāo)量時(shí)間序列進(jìn)行相空間重構(gòu)，得到符合要求的訓(xùn)練集和測(cè)試集。利用C-C法求解最優(yōu)的嵌入維數(shù)m和延遲時(shí)間τ。得到時(shí)間窗τw=13，延遲時(shí)間τ=4，計(jì)算可得嵌入維數(shù)m=4。

(2)樣本歸一化

支持向量機(jī)對(duì)零均值方差為1的數(shù)值最敏感，為了減小模型訓(xùn)練誤差，對(duì)重構(gòu)后的訓(xùn)練集和測(cè)試集進(jìn)行歸一化處理:

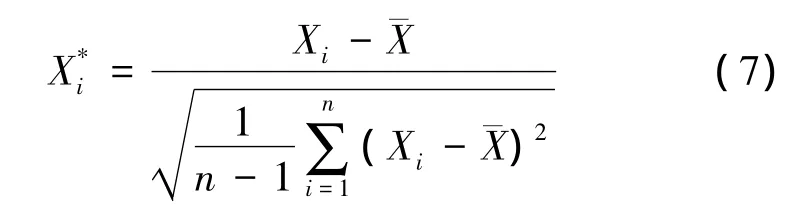
(3)核函數(shù)參數(shù)和SVM參數(shù)的選擇

使用k-折交叉驗(yàn)法尋找最優(yōu)參數(shù)，k取5，誤差評(píng)價(jià)指標(biāo)為均方根誤差RMSE，得到的最優(yōu)參數(shù)組合為(C，σ，ε)=(0.329 88，21.112 1，0.094 6)。

(4)模型的訓(xùn)練和測(cè)試

利用上步得到的最優(yōu)參數(shù)組合，通過SMO[12]算法訓(xùn)練SVM模型，并對(duì)訓(xùn)練得到的模型進(jìn)行測(cè)試。為了說明SVM模型的有效性，還分別使用了最大Lyapunov指數(shù)法、一階加權(quán)局域法和RBF神經(jīng)網(wǎng)絡(luò)法對(duì)重構(gòu)樣本做了訓(xùn)練和預(yù)測(cè)。

3.2 實(shí)驗(yàn)結(jié)果及分析

圖1為最大Lyapunov指數(shù)法和一階加權(quán)局域法的預(yù)測(cè)結(jié)果。由于這兩種方法預(yù)測(cè)速度很慢，所以只用來預(yù)測(cè)了50步。從圖中可以看出，但這兩種方法對(duì)陀螺隨機(jī)漂移的預(yù)測(cè)都不太理想。

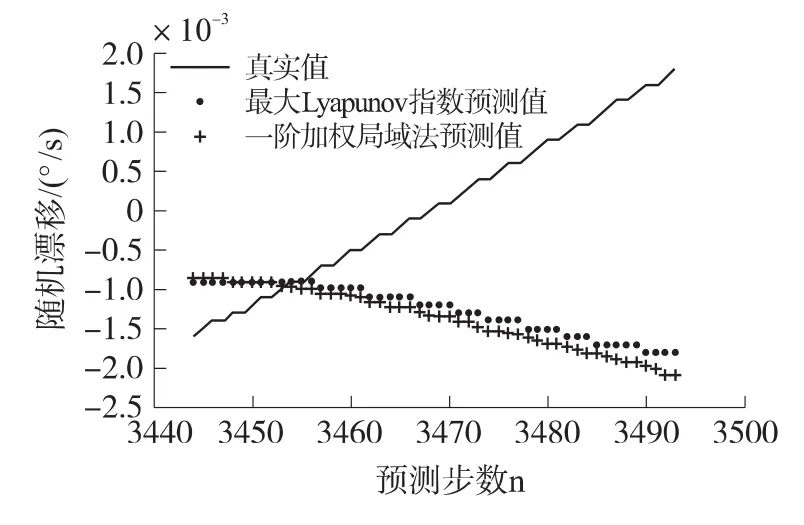
圖1 最大Lyapunov指數(shù)法和一階加權(quán)局域法的預(yù)測(cè)結(jié)果

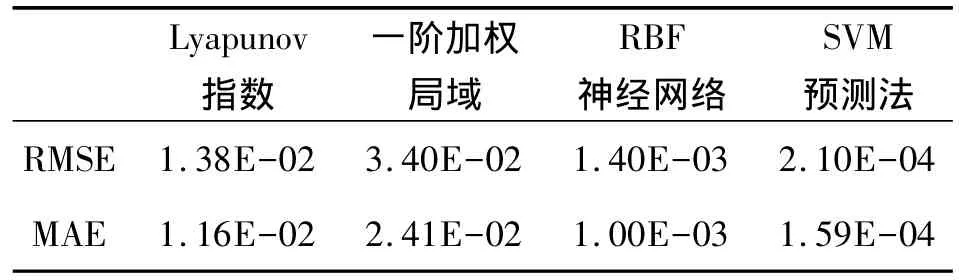
表1 幾種方法對(duì)測(cè)試集的預(yù)測(cè)結(jié)果

圖2和圖3所示分別為RBF神經(jīng)網(wǎng)絡(luò)方法與SVM法對(duì)訓(xùn)練集的預(yù)測(cè)絕對(duì)誤差和對(duì)測(cè)試集的預(yù)測(cè)效果，表1記錄了4種方法對(duì)測(cè)試集預(yù)測(cè)的均方根誤差RMSE和平均絕對(duì)誤差MAE。從以上圖表可得到結(jié)論:

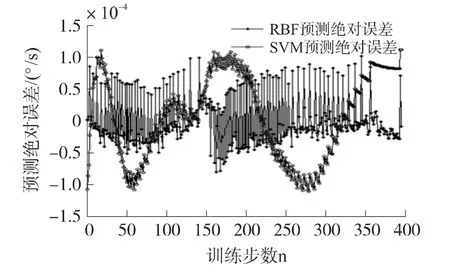
圖2 RBF法和SVM法對(duì)訓(xùn)練集的預(yù)測(cè)絕對(duì)誤差

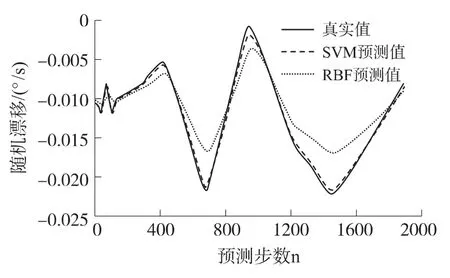
圖3 RBF法和SVM法對(duì)測(cè)試集的預(yù)測(cè)結(jié)果

(1)對(duì)于相同的訓(xùn)練集，RBF神經(jīng)網(wǎng)絡(luò)法和SVM法相比，具有更高的訓(xùn)練精度。

(2)對(duì)于相同的測(cè)試集，SVM法比RBF神經(jīng)網(wǎng)絡(luò)法的預(yù)測(cè)效果要好，能夠更好的預(yù)測(cè)出陀螺隨機(jī)漂移的變化趨勢(shì)。

(3)SVM法的預(yù)測(cè)誤差隨著預(yù)測(cè)步數(shù)的增加而不斷增大。

造成以上結(jié)果的原因是:RBF神經(jīng)網(wǎng)絡(luò)法是一種基于風(fēng)險(xiǎn)經(jīng)驗(yàn)最小化準(zhǔn)則的學(xué)習(xí)算法，它的訓(xùn)練過程力求對(duì)訓(xùn)練集做到最好的擬合，而忽視了模型結(jié)構(gòu)固有的置信風(fēng)險(xiǎn)，因此預(yù)測(cè)效果受到模型自身缺陷的限制。SVM法以結(jié)構(gòu)風(fēng)險(xiǎn)最小為學(xué)習(xí)準(zhǔn)則，既兼顧訓(xùn)練集的擬合精度，又重視置信風(fēng)險(xiǎn)的減小，因而具有較好的泛化能力，能取得更好的預(yù)測(cè)效果。

由于陀螺隨機(jī)漂移時(shí)間序列的非線性和弱時(shí)變特征，造成訓(xùn)練模型的預(yù)測(cè)精度隨預(yù)測(cè)步數(shù)的增加而增大，訓(xùn)練得到的模型只能做短時(shí)預(yù)測(cè)。為了提高全程的預(yù)測(cè)精度，每隔一定時(shí)間以新加入的樣本為訓(xùn)練集，而對(duì)于器件的同一次工作，可以保持模型的各個(gè)參數(shù)不變，重新訓(xùn)練預(yù)測(cè)模型。3個(gè)軸向的模型訓(xùn)練可以間隔進(jìn)行，模型的訓(xùn)練耗時(shí)很少，對(duì)系統(tǒng)的正常工作的實(shí)時(shí)性影響不大。

4 總結(jié)

本文將基于機(jī)器學(xué)習(xí)理論的支持向量機(jī)法，用于MEMS陀螺儀隨機(jī)漂移的建模和補(bǔ)償。通過相空間重構(gòu)將問題轉(zhuǎn)換為支持向量機(jī)所需要的形式，利用最優(yōu)化算法求得了相空間重構(gòu)、核函數(shù)和預(yù)測(cè)模型的各項(xiàng)參數(shù)。仿真結(jié)果表明，該方法克服了傳統(tǒng)方法的不足，能夠很好的預(yù)測(cè)陀螺的隨機(jī)漂移，可以用于實(shí)際工程中MEMS陀螺儀隨機(jī)漂移的補(bǔ)償。

[1]張英，戚紅向.航天慣導(dǎo)產(chǎn)品及技術(shù)發(fā)展簡介[J].航天標(biāo)準(zhǔn)，2010(3):40－43.

[2]陳殿生，邵志浩，雷旭升.MEMS陀螺儀隨機(jī)誤差濾波[J].北京航空航天大學(xué)學(xué)報(bào)，2009，35(2):246－250.

[3]方靜，尚捷，顧啟泰.光纖陀螺隨機(jī)誤差建模的實(shí)驗(yàn)研究[J].傳感技術(shù)學(xué)報(bào)，2008，21(9):1514－1517.

[4]李杰，張文棟，劉俊.基于時(shí)間序列分析的Kalman濾波方法在MEMS陀螺儀隨機(jī)漂移誤差補(bǔ)償中的應(yīng)用研究[J].傳感技術(shù)學(xué)報(bào)，2006，19(5):2215－2219.

[5]盧海曦，夏敦柱，周百令.基于遺傳小波神經(jīng)網(wǎng)絡(luò)的MEMS陀螺誤差建模[J].中國慣性技術(shù)學(xué)報(bào)，2008，16(2):216－219.

[6]Vapnik V N.The Nature of Statistical Learning Theory[M].New York:Springer-Verlag，1995:35－46.

[7]趙志宏，楊紹普.基于SVM的混沌時(shí)間序列分析[J].動(dòng)力學(xué)與控制學(xué)報(bào)，2009，7(1):5－8.

[8]Smola A J，Schoelkopf B.A Tutorial on Support Vector Regression[J].Statistics and Computing，2004(14):199－222.

[9]呂金虎.混沌時(shí)間序列分析及其應(yīng)用[M].武漢:武漢大學(xué)出版社，2002:66－71.

[10]Ito K，Nakano R.Optimizing Support Vector Regression Hyper-Parameters Based on Cross Validation[J].Proceedings of the International Joint Conference on Neural Networks，2003(7):2077－2082.

[11]王曉蘭，康蕾.在線模糊最小二乘支持向量機(jī)的時(shí)間序列預(yù)測(cè)[J].計(jì)算機(jī)工程與應(yīng)用，2010，46(9):215－240.

[12]Keerthi S，Shevade S K.SMO Algorithm for Least-Squares SVM Formulation[J].Neural Computation，2003，15(2):487－507.