可靠通信的多跳水聲網絡能量最小路徑*

王 琛，方彥軍

(武漢大學自動化系，武漢430072)

近年來，隨著人類海洋活動的日益頻繁，水聲傳感器網絡以其在海洋資源勘探、環境監測以及軍事防御等眾多領域的應用潛力，引起了國內外研究學者的廣泛關注[1－3]。由于水聲網絡的節點通常由電池供電，而目前水下充電技術尚不成熟，且在水下大范圍更換電池成本太高，因此降低節點能耗以延長網絡生命期就顯得尤為重要。

目前已有許多針對降低水聲網絡能耗的路由協議和 MAC(Medium Access Control)協議被提出[4－8]，但并未重視水聲信號的傳播特性。文獻[9]在分析水聲信號傳播特性后指出，多跳模式可以有效減少節點功耗，同時能增加可用帶寬，有望成為下一代水聲網絡的組網策略;在此基礎上，文獻[10]指出直線等距的多跳網絡模型相對于二維或三維模型能耗更低，但并未給出理論證明。與之類似的問題在無線傳感器網絡中也有研究，如文獻[11－12]分別證明了AWGN信道和多跳網絡的總能耗在直線等距的拓撲下最低。

不過，與陸地無線信道相比，水下信道的傳輸條件要惡劣得多，數據包在傳輸過程中發送失敗、丟包等情況更為頻繁[13]，為保證水下網絡的可靠通信，通常會有鏈路層的恢復機制(如檢錯重發或使用前向糾錯碼等)，由此而帶來的能耗在前述對能量最小路徑的研究中并未考慮。

本文通過建立可靠通信的多跳水聲網絡能耗模型，研究給定接收信噪比條件下的網絡能量最小路徑問題，證明了可變發送功率和固定發送功率兩種模式下，直線等距網絡的總能耗最小，并給出最優跳數和最優距離的求解方法。

1 系統模型

1.1 水聲傳播損失與噪聲

根據Urick的傳播模型[14]，頻率為 f kHz的水聲信號傳輸距離d km時的傳播損失A(d，f)的分貝形式為:

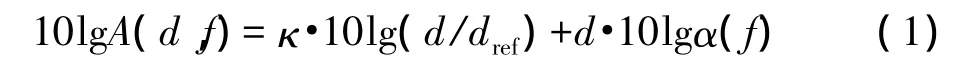
等式(1)右邊第1部分為擴展損失，第2部分為衰減損失。式中dref為參考距離(通常取值為1 m)，κ為衰減因子(一般介于1到2之間);α(f)為頻率性的吸收系數(單位為dB/km)，可通過Thorp公式[15]得到。在某些較低的頻率區域，α(f)常由下面的經驗公式獲得[16]:

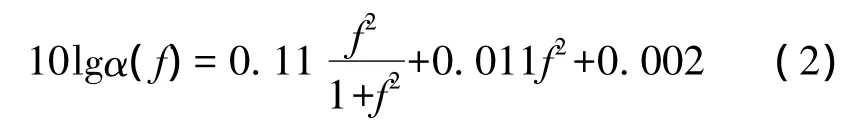
水下環境噪聲受潮汐、湍流、海面的風浪、船舶擾動及熱噪聲等多種因素的影響，其功率譜密度N(f)隨載波頻率的升高而降低，在特定的頻率區間可采用如下經驗公式近似表示[16]

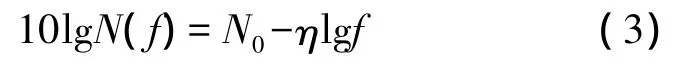
其中 N0=50 dB re μ Pa，η=18 dB/decade。

本文假設 κ=1.5，α(f)和 N(f)分別由式(2)和式(3)計算得出。

1.2 多跳網絡模型

考慮一個二維多跳網絡模型，源節點和目的節點相距為D，通過任意分布的K－1個中繼節點進行數據通信(如圖1所示)。源節點用N0表示，目的節點用Nk表示，中繼節點表示為Ni，i=1，…，K－1，其中K 為跳數。采用文獻[17]中的表示，設第i條鏈路的距離di滿足di=φiD，不難得出(其中代表直線路徑)。

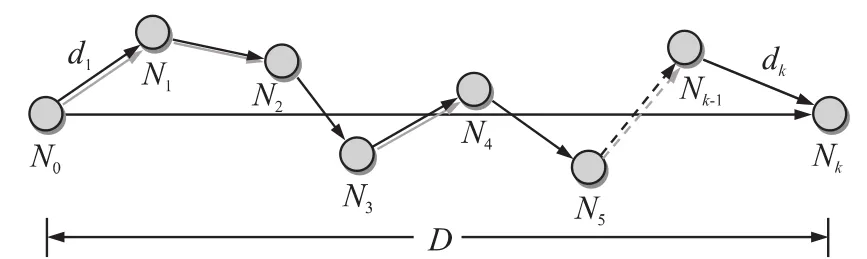
圖1 二維多跳網絡模型

對此網絡模型做如下假設:(1)節點只能半雙工通信，這意味著節點不能同時處于發送和接收狀態;(2)鏈路的連通性僅限于相鄰的兩個節點之間，因此不考慮節點間的合作機制以及網絡的空間重用;(3)節點可以選用固定發送功率和可變發送功率兩種模式，但同一網絡中各節點所用模式相同;(4)每個節點都具備檢錯重發數據的功能。

1.3 可靠通信的能量模型

一條鏈路傳輸一個數據包所需的能耗E包括發送數據包的能耗Et和接收并處理數據包的能耗Ec:

Et可通過發送功率Pt乘以發送時間得到，L為數據包長(單位bit)，ρ為調制帶寬效率(單位bit/s/Hz)，B(d)為可用帶寬(單位 kHz)，隨距離的增加而變小[10]。對于給定的目標接收信噪比γtgt，

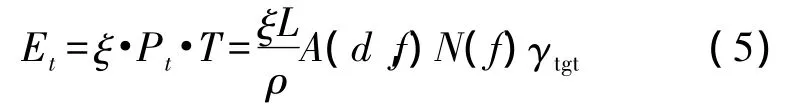
其中ξ是聲功率(單位為dB re μ Pa)轉換為電功率(單位為 Watt)的轉換系數。

Ec與鏈路的距離無關，且通常遠小于Et，因此本文假設Ec為固定值。則式(4)可轉化為

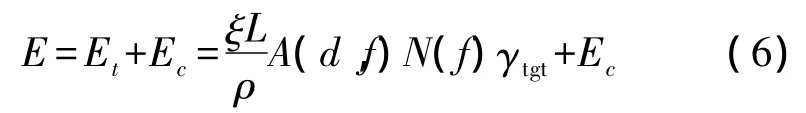
若設鏈路誤包率為p，則確保數據包傳輸成功所需的發送次數是一個幾何分布的隨機變量，且平均發送次數為1/(1－p)[18]。因此，鏈路可靠傳輸一個數據包的能耗

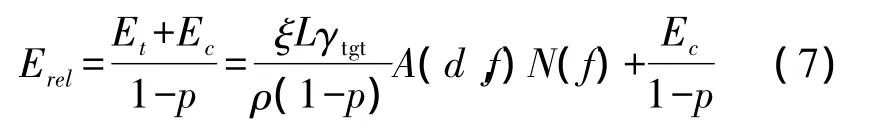
2 AN積的簡化

從式(7)可以看出，鏈路可靠傳輸的能耗主要取決于A(d，f)N(f)(簡稱AN積)，其包含傳輸距離d和信號頻率f兩個變量，研究起來比較復雜。本節將研究AN積的性質，尋求f和d之間的關系，以便簡化計算。

2.1 AN積的性質

由式(1)～式(3)可得出分貝形式的AN積:

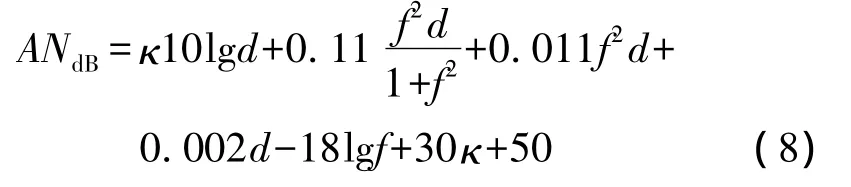
圖2畫出了不同傳輸距離時的AN積與信號頻率的關系。從圖2可以看出有如下性質。

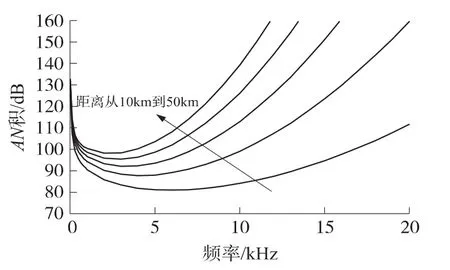
圖2 不同傳輸距離時的AN積與信號頻率的關系

性質1對于給定的傳輸距離d，存在一個最優頻率fo(d)使AN積最小，即

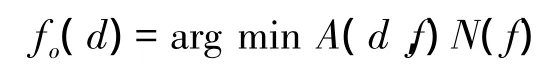
證明 將ANdB對f求導，其一階導數滿足

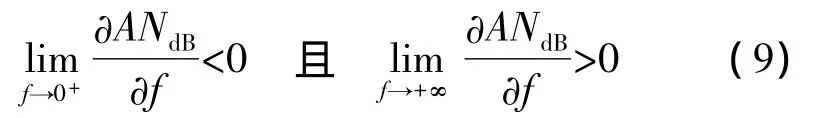
故存在頻率f=fo(d)使

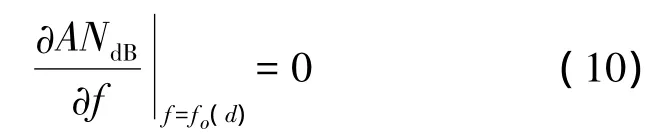
此時ANdB達到最小值。證畢。

2.2 d與fo(d)的關系

性質1表明，距離為d的鏈路采用fo(d)作為信號頻率時AN積最小。若能得出d與fo(d)的函數關系，則可將式(7)轉化為僅含d一個變量的表達式。為此，將ANdB對d求導，并令其一階導數為零

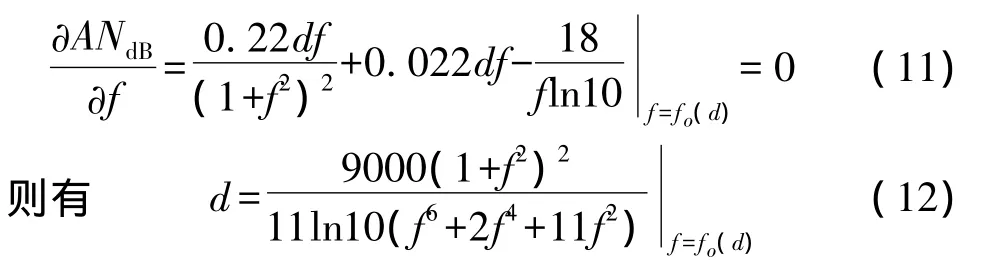
從上式無法得到fo(d)關于d的閉式解。為此，將上式的數值解通過MATLAB曲線擬合得到兩個擬合度較好的曲線 fo(d)=adβ和 fo(d)=adβ+χ，其參數見表1，其中SSE(Sum of Squares due to Error)為和方差，RMSE(Root Mean Squared Error)為均方根。注意到式(12)中f均為偶次方冪，而擬合曲線中參數β與0.5十分接近，因此我們采用如下函數作為擬合曲線以簡化計算:

表1 最優頻率擬合曲線及其參數

其 SSE 為2.6207，RMSE 為0.2196。圖3給出了該曲線(實線)與數值解(圓圈)的示意圖，從圖3可以看到，該曲線擬合度令人滿意。

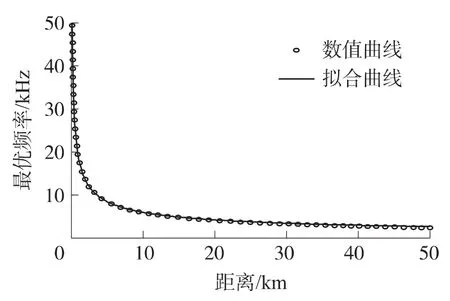
圖3 最優頻率與距離的關系

2.3 AN積的簡化表達

將式(13)代入式(8)即可得到

注意到g(d)是d的單調遞增函數，因為g'(d)＞0。

3 能量最小路徑分析

本節利用第2節得到的AN積的近似表達式來分析可變發送功率VTP(Variable Transmission Power Strategy)和固定發送功率FTP(Fixed Transmission Power Strategy)兩種情況下的能量最小路徑。

在可變功率情況下，節點通過調整發送功率以保證信號到達目的節點時有相同的目標接收信噪比γtgt。在此情況下，若各鏈路信號頻率變化不大時，傳輸距離越大的鏈路需要越高的發送功率。

在固定功率情況下，各節點的發送功率相同。為保證各鏈路的接收信噪比不低于γtgt，此時各鏈路的發送功率應選擇AN積最大鏈路的發送功率。盡管與可變功率相比，固定功率對能量的利用效率明顯較低，但對其研究也是必要的，因為目前大部分水聲節點不具備調節發送功率的功能。

3.1 可變功率的能量最小路徑

由式(7)，鏈路i的可靠傳輸能耗

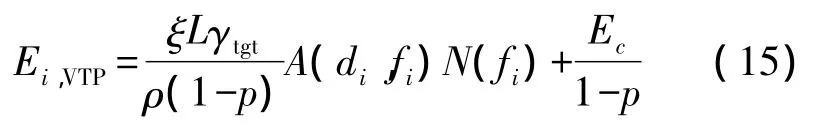
則網絡可靠傳輸的總能耗為

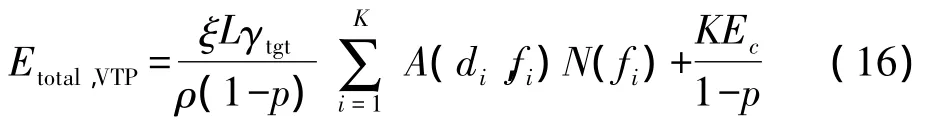
將近似的AN積代入，則可變功率的能量最小路徑問題可以轉化為以下優化問題:

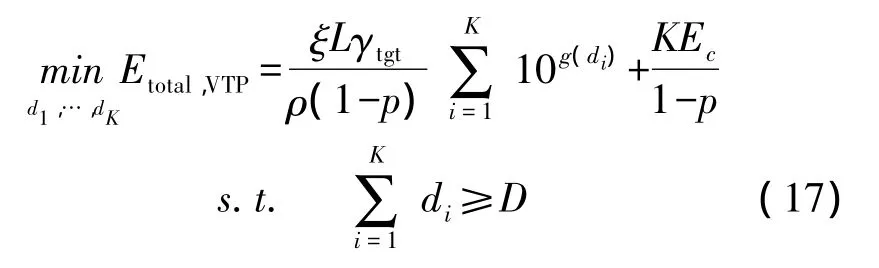
其中變量為di。該優化問題的解由以下定理給出。

定理1對于節點任意分布的多跳水聲網絡，若各節點采用可變功率模式，且各鏈路接收信噪比不低于給定的目標接收信噪比，則直線等距路徑使可靠傳輸的網絡總能耗最小。

證明 構造該優化問題的拉格朗日函數

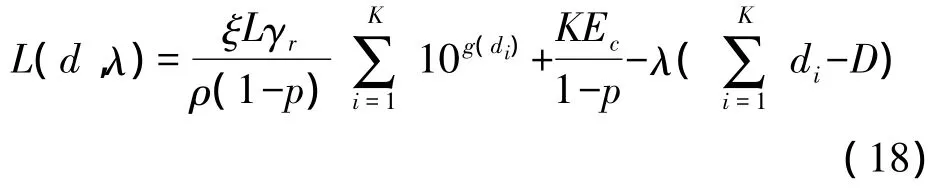
其中 λ≥0 為拉格朗日乘子，d=(d1，d2，…，dK)。則其KKT條件(Karush-Kuhn-Tucker Condition)為:

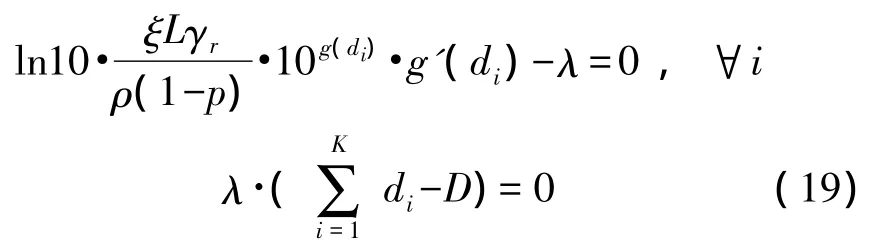
由第1組優化條件可知，對任意的i，Χ(di)=10g(di)·g'(di)為固定值，由 Χ(d)=10g(d)·g'(d)的單調性(Χ'(d)＞0)可知 d1=d2=…=dK，為等距網絡;同時，第一組條件表明λ0，因此不難從第2個條件得出，為直線網絡;進而可得KKT對，其中 λ*可由式(19)得出。另一方面，考察其切空間中的任意 y≠0，有 yTH(d*，λ*)y＞0，其中H(d*，λ*)為該優化問題的拉格朗日函數在(d*，λ*)處的 Hesse矩陣[19]，故能保證 KKT 條件的充分性。綜上可知，直線等距網絡能使可變功率情況下的網絡能耗最小。證畢。

3.2 固定功率的能量最小路徑

固定功率情況下，鏈路i的能耗取決于所有鏈路中AN積最大鏈路的能耗，即

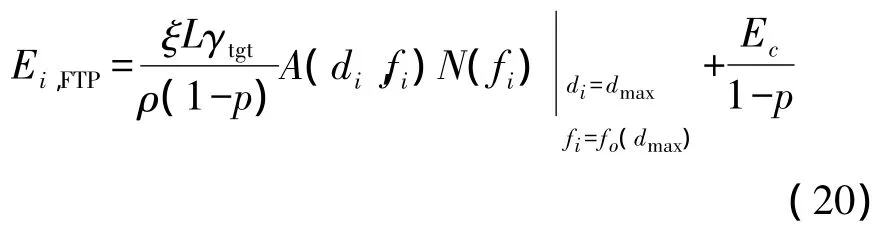
由于各鏈路發送功率相同，因此可靠發送一個數據包的總能耗

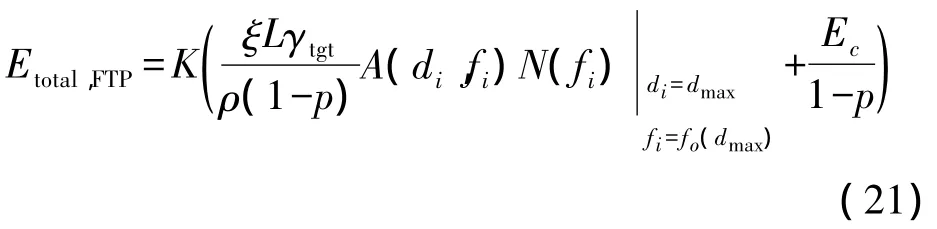
將近似的AN積代入，則固定功率的能量最小路徑問題可以轉化為以下優化問題:

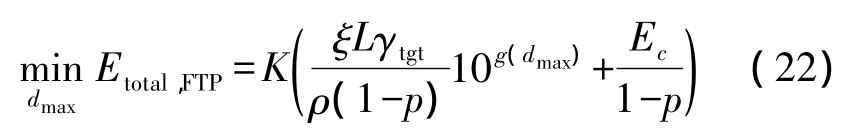
其中變量為 dmax。該優化問題的解由以下定理給出。

定理2對于節點任意分布的多跳水聲網絡，若各節點采用固定功率模式，且各鏈路接收信噪比不低于給定的目標接收信噪比，則直線等距路徑使可靠傳輸的網絡總能耗最小。

證明 不難看出，Etotal，FTP是關于dmax的單調遞增函數，因此式(22)與下面的式子等價:

因為 di≤dmax，所以;而，則Kdmax≥D，故，即

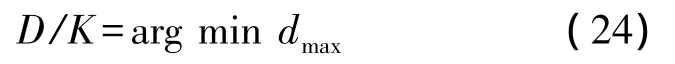
此即表明直線等距網絡能使固定功率情況下的網絡能耗最小。證畢。

3.3 最優跳數與最優距離

既然可靠通信的能量最小路徑是直線等距網絡，那么自然需要考慮一個問題，即各節點相距多少能使能耗最少?也就是，使能耗最小的最優跳數是多少?

因此，考慮直線等距網絡的總能耗

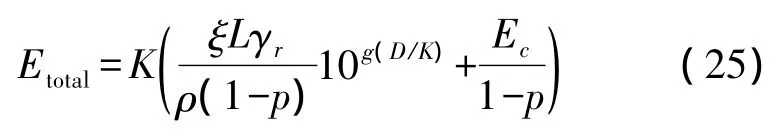
把K視為連續量，將上式對K求導并令其一階導數為零可得

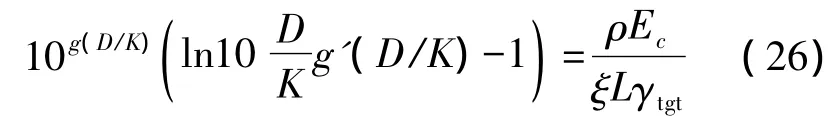
若令d*為方程的解，則最優跳數

其中k*為自然數，d*可通過數值方法求得。此時網絡的最優能耗為

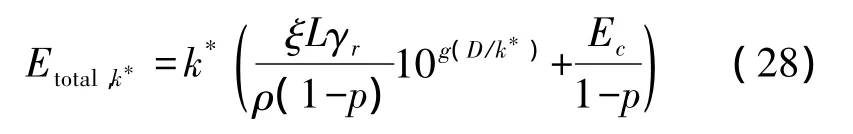
4 仿真結果

本節對第3節的定理進行驗證，并對直線等距網絡的最優跳數和最優距離進行仿真。仿真中只考慮直線網絡的情況(即)，因為在同樣的節點分布時非直線網絡能耗顯然更高。仿真試驗的參數設置如下:誤包率 p=0.1，調制帶寬效率 ρ=0.5，聲－電功率轉換系數 ξ=4×10－17，數據包長度 L=256 byte，接收能耗Ec=0.5 J，目標接收功率信噪比 γtgt=20 dB。

圖4比較了不同節點位置時可變功率和固定功率模式下的能耗與距離的關系。從圖中可以看出，不論是2跳或是3跳網絡，等距時的能耗最低，這與第3節的理論相符。同時可以看出，當節點位置相同時，固定功率模式較可變功率模式能耗更高，這是由于固定功率模式下，各鏈路發送功率均選擇AN積最大鏈路的發送功率，以犧牲能耗為代價來證各鏈路的接收信噪比不低于γtgt。

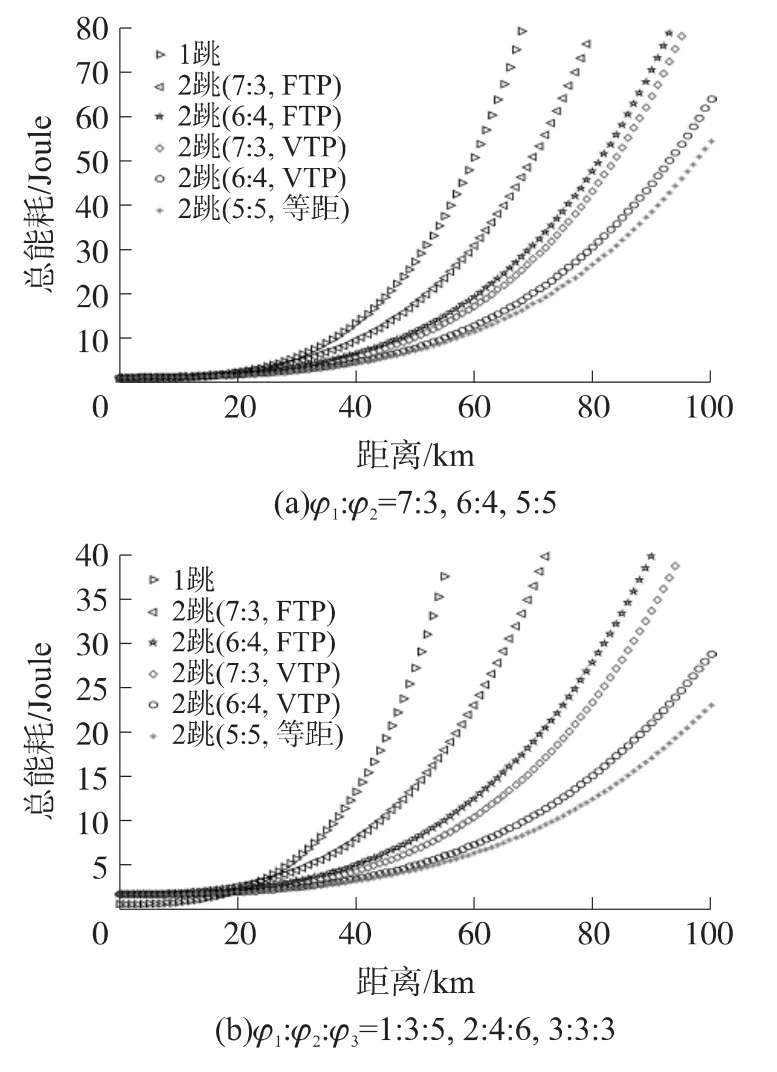
圖4 不同節點位置時能耗與距離的關系比較

圖5描繪了直線等距網絡在傳輸距離從10 km到100 km時總能耗與跳數的關系。從圖中能明顯看出，對不同的傳輸距離，存在一個最優跳數使總能耗最低，且距離越長，最優跳數越大。

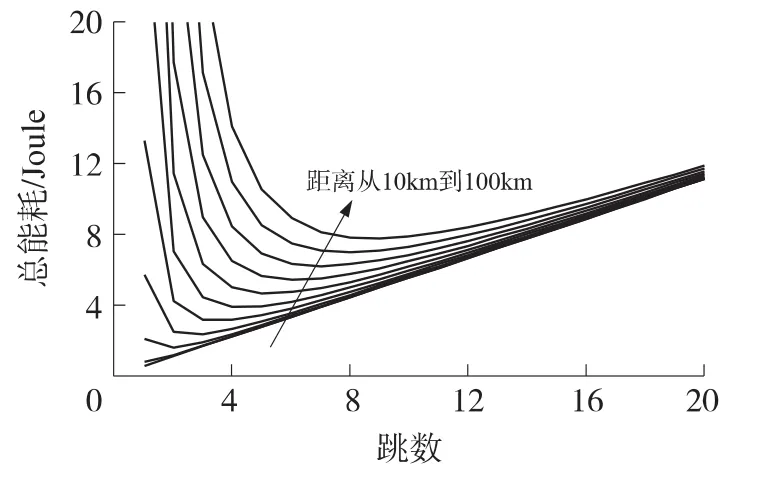
圖5 直線等距網絡在不同距離時總能耗與跳數的關系

圖6給出了直線等距網絡在跳數從1到12時總能耗與傳輸距離的關系，可以看出，在某一段距離區間內，存在一個最優跳數使總能耗最低，且相鄰跳數的總能耗與跳數關系曲線之間的交點(小圓圈)，其連線近似為一條直線，印證了式(27)中最優跳數與最優距離近似的線性關系，而相鄰交點間的距離也近似相等(約13 km)，即為最優距離。

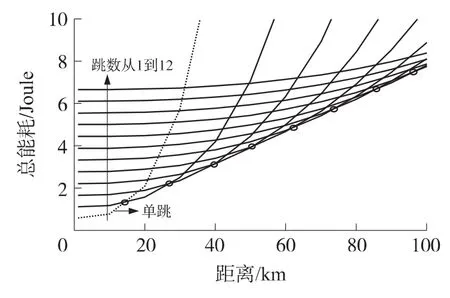
圖6 直線等距網絡在不同跳數時總能耗與距離的關系

此外，從圖4～圖6都能看出，在較短傳播距離(k＜15 km)時，單跳較多跳能耗更低，這也說明并非任何情況下都是多跳能耗更優。

5 結束語

本文研究了可靠傳輸條件下多跳水聲網絡的能量最小路徑。建立了二維的網絡能量模型，通過曲線擬合的方法得到了最優頻率－距離的近似表達式，并利用該表達式分析了可變功率和固定功率兩種模式下的能量最小路徑。結果表明，無論對于可變功率還是固定功率的多跳水聲網絡，其可靠傳輸時直線等距網絡能使總能耗最小。考慮直線等距網絡，本文還給出了使能耗最小的最優跳數和最優距離。所得結果對于近岸環境監測網絡的實現有一定的指導意義。

[1]Heidemann J，Mitra U，Preisig J，et al.Underwater Wireless Communication Networks(Guest Editorial)[J].IEEE Journal on Selected Areas in Communications，2008，26(9):1617－1619.

[2]呂超，王碩，譚民.水下移動無線傳感器網絡研究綜述[J].控制與決策，2009，24(6):801－807.

[3]郭忠文，羅漢江，洪鋒，等.水下無線傳感器網絡的研究進展[J].計算機研究與發展，2010，47(3):377－389.

[4]鐘永信，黃建國，韓晶.基于空間喚醒的水聲傳感器網絡節能路由協議[J].電子與信息學報，2011(6):1326－1331.

[5]Lee U，Wang P，Noh Y，et al.Pressure Routing for Underwater Sensor Networks[C]//IEEE INFOCOM，San Diego，CA，USA，2010:1－9.

[6]劉玉梁，潘仲明.水下無線傳感器網絡能量路由協議的仿真研究[J].傳感技術學報，2011，24(6):905－908.

[7]王錦程，李德識.一種基于水聲信道的無線傳感器網絡路由協議[J].傳感技術學報，2009，22(1):107－110.

[8]Park M K，Rodoplu V.Uwan-Mac:An Energy-Efficient Mac Protocol for Underwater Acoustic Wireless Sensor Networks[J].IEEE Journal of Oceanic Engineering，2007，32(3):710－720.

[9]Stojanovic M，Preisig J.Underwater Acoustic Communication Channels:Propagation Models and Statistical Characterization[J].IEEE Communications Magazine，2009，47(1):84－89.

[10]Zorzi M，Casari P，Baldo N，et al.Energy-Efficient Routing Schemes for Underwater Acoustic Networks[J].IEEE Journal on Selected Areas in Communications，2008，26(9):1754－1766.

[11]Bae C，Stark W E.On Minimum Energy Routing in Wireless Multihop Networks[C]//Information Theory and Applications Workshop，San Diego，CA，USA，2009:346－350.

[12]Zhang R，Gorce J M.Optimal Transmission Range for Minimum Energy Consumption in Wireless Sensor Networks[C]//IEEE Wireless Communications and Networking Conference(WCNC)，Las Vegas，Nevada，USA，2008:757－762.

[13]Liu L，Zhou S，Cui J H.Prospects and Problems of Wireless Communication for Underwater Sensor Networks[J].Wireless Communications and Mobile Computing，2008，8(8):977－994.

[14]Urick R J.Principles of Underwater Sound[M].New York:McGraw-Hill，1983.

[15]Berkhovskikh L，Lysanov Y.Fundamentals of Ocean Acoustics[M].New York:Springer，1982.

[16]Stojanovic M.On the Relationship between Capacity and Distance in an Underwater Acoustic Communication Channel[J].ACM SIGMOBILE Mobile Computing and Communications Review(MC2R)，2007，11(4):34－43.

[17]Bae C，Stark W E.End-to-End Energy-Bandwidth Tradeoff in Multihop Wireless Networks[J].IEEE Transactions on Information Theory，2009，55(9):4051－4066.

[18]Banerjee S，Misra A.Minimum Energy Paths for Reliable Communication in Multi-Hop Wireless Networks[C]//ACM International Symposium on Mobile Ad Hoc Networking ＆ Computing(MobiHoc)，EPFL Lausanne，Switzerland，2002:146－156.

[19]Borwein J M，Lewis A S.Convex Analysis and Nonlinear Optimization:Theory and Examples[M].Springer Verlag，2006.