鋼筋混凝土梁的優化設計

曾彬峻，李文興

(桂林理工大學土木與建筑工程學院，廣西 桂林 541004)

0 引 言

在工程建筑物中，矩形鋼筋混凝土梁是一種很常見的受力構件，所以探討此類構件的優化設計問題具有一定的現實意義.建筑物中梁板結構部分的造價占總結構造價的50%左右，梁設計的合理與否對結構工程造價的影響起到至關重要的作用.優化設計的方法有很多，包括拉格朗日乘子法、復形法、模糊優化法、罰函數法等等.而近來很多研究者又采用各種優化方法的改進方法進行優化設計，譬如模糊動態罰函數法、模糊罰函數遺傳算法等，但是最有效的方法還是罰函數法[1].應用罰函數對鋼筋混凝土進行優化已有很多學者進行過研究，基本都是基于單調的一種材料組合下進行截面、經濟效益的優化，因此本文采用罰函數法，并結合MATLAB的優化工具箱對多種材料組合進行研究，先得出每一組的優化結果，然后從所有實驗組里選出最優、最經濟的設計.

1 優化設計原理

罰函數法針對約束函數構造適當的中間函數，并引入罰因子將約束條件引入到目標函數中構成無約束目標函數，對于約束優化問題，罰函數的一般形式為[2]：

(1)

式(1)中：φ[hv(x)]和ψ[gu(x)]分別為根據等式約束hv(x)和不等式約束gu(x)構造的中間函數，恒為非負.r1和r2為罰因子或罰參數，是大于零的實數，根據中間函數的特性，罰因子的值在迭代過程中會不斷變化.中間函數與罰因子的乘積稱為懲罰項，在設計變量取值接近邊界的過程中，罰因子與中間函數朝相反的方向變化，但在無限逼近的過程中懲罰項趨于零.當約束條件未被滿足時，罰因子越大，罰函數的值也越大，不符合罰函數極小化的目的，所以罰函數內包含了當約束條件未被滿足時在目標函數上所受的“懲罰”[3].

隨著罰因子的不斷調整，無約束最優解會不斷的逼近有約束的最優解，所以罰函數法其實是一種序列無約束極小化方法，簡稱“SUMT”法.SUMT的方法有很多，從原理上可以分為：外點法，內點法和混合法.在本文中是采用混合罰函數法對鋼筋混凝土梁進行最優值求解.

混合罰函數法[2]是把外點法和內點法結合起來，不等式是約束采用內點法，等式約束采用外點法.對于一半形式優化問題：

min(max)f(x)=f(x1,x2,...,xn)，x∈Rn

(2)

滿足gu(x)≤(≥)0，u=1,2,...,L

hv(x)=0,v=1,2,...,M

混合罰函數的具體形式為：

(3)

混合罰函數法的迭代過程如下：

a.選擇初始迭代點x(0)，合適的初始罰因子及罰因子r(0)遞減速率c，且計數k=0；

b.對不等式約束按內點法構造中間函數，對等式約束按外點法構造中間函數；

c.令k=k+1;r(k)=cr(k+1)進行迭代;

d.判斷迭代是否滿足精度要求：|f(x(k))-l(x(k)),r(k)|<ε，k=1,2,...n，如果不等式成立且滿足迭代過程結束，以x(k)作為最優解x*的最終近似值，否則轉到第(3)步繼續迭代.

2 鋼筋混凝土梁的優化設計

2.1 模型建立

本文以單筋混凝土簡支梁為例，其計算簡圖如圖1所示：

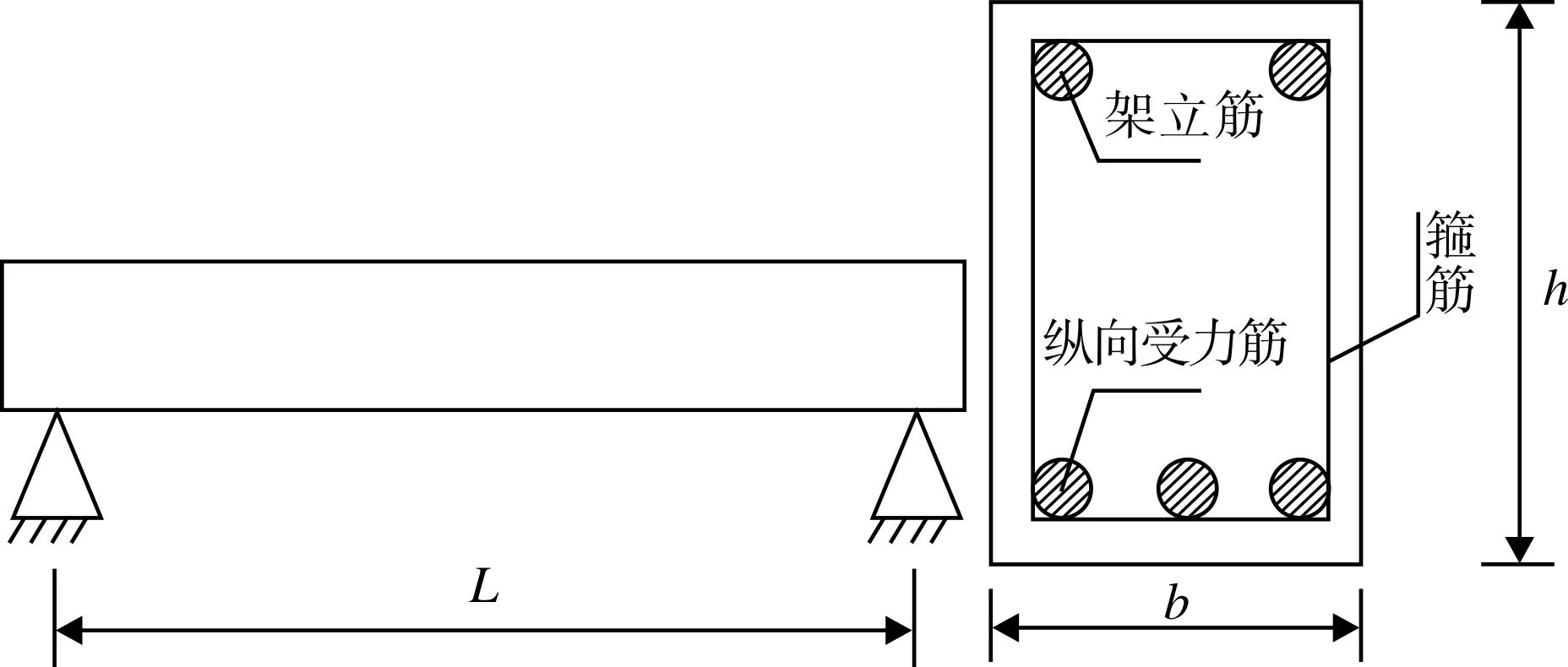
圖1 優化設計計算簡圖Fig.1 Optimal design diagram

2.2 變量設計

由于鋼筋混凝土的優化設計是一個多變量的，多約束，非線性的優化設計，所以等截面矩形梁本身的材料費用取決于混凝土的造價和鋼筋的造價之和.混凝土的造價取決于截面的尺寸(即b和h)，而鋼筋的造價包括(架立筋，受力筋，箍筋)的造價，對于單筋梁時，架立筋是按照構造配筋的，所以不會發生變化，箍筋也是按照構造配筋的但是隨梁高變化，但是不太靈敏，所以鋼筋造價跟受力筋的面積As的變化相關.

2.3 目標函數

本文僅計入混凝土的造價，鋼筋的造價，混凝土的強度和鋼筋的強度，考慮到是等截面梁，所以目標函數[4]假定為：

Z=bhZe+AsZs

(4)

式(4)中：Ze、Zs為混凝土受拉縱筋As的單位造價，元/m3.

2.4 約束條件

2.4.1 正截面承載力要求[5]

(5)

fyAs=fcbx

(6)

式(5)中：M為彎矩設計值；fc為混凝土彎曲抗壓強度設計值；B為梁的截面寬度；h為梁的截面高度；x為混凝土受壓區高度.

2.4.2 最小配筋率要求

Y2=As-ρminb(h-as)≥0

(7)

式(7)中：按規范規定取的縱向受拉鋼筋最小配筋率.

2.4.3 最大配筋率要求

Y3=ξ-ξb≤0

(8)

(9)

式(8)中：ξb表示鋼筋界限受壓區高度

2.4.4 斜截面承載力要求(構造配筋)

Y4=V-0.7ftb(h-as)≤0

(10)

式(10)中：ft表示混凝土軸心受拉強度設計值.

2.4.5 梁的尺寸控制

Y5=b≥b0

(11)

Y6=h≥h0

(12)

式(11)中：b0和h0分別表示梁寬度和高度的下限值.

2.5 優化數學模型

由(5)到(13)，X=[b,h,As]T及minf(x)=Z=bhZe+AsZs組成.

3 MATLAB的優化求解

MATLAB優化工具箱是面向最優化問題求解的專用工具箱，具有強大的科學計算能力，含有一系列的優化算法函數，對各種優化問題提供了一個完整的解決方案，主要包括線性規劃、二次規劃、非線性規劃、最小二乘法問題、非線性方程求解、多目標優化、最小最大問題、以及半無限問題等等的優化問題.在土木工程領域中，結構優化問題大多數都是多變量、非線性約束的最優化問題，因此使用MATLAB優化工具箱中的fmincon函數進行求解，其具體的數學模型可以用式(13)形式表示：

(13)

式(13)中：x,b,beq,lb和ub為向量；A和Aeq為矩陣；C(x)和Ceq(x)為函數向量，分別表示非線性不等式和非線性等式約束；f(x)為標量函數.

fmincon的具體調用的一般形式為：x=fmincon(fun,x0,A,b)，其中fun為目標函數，x0為迭代初值.對于鋼筋混凝土梁的最優化設計問題的具體流程如圖2所示.

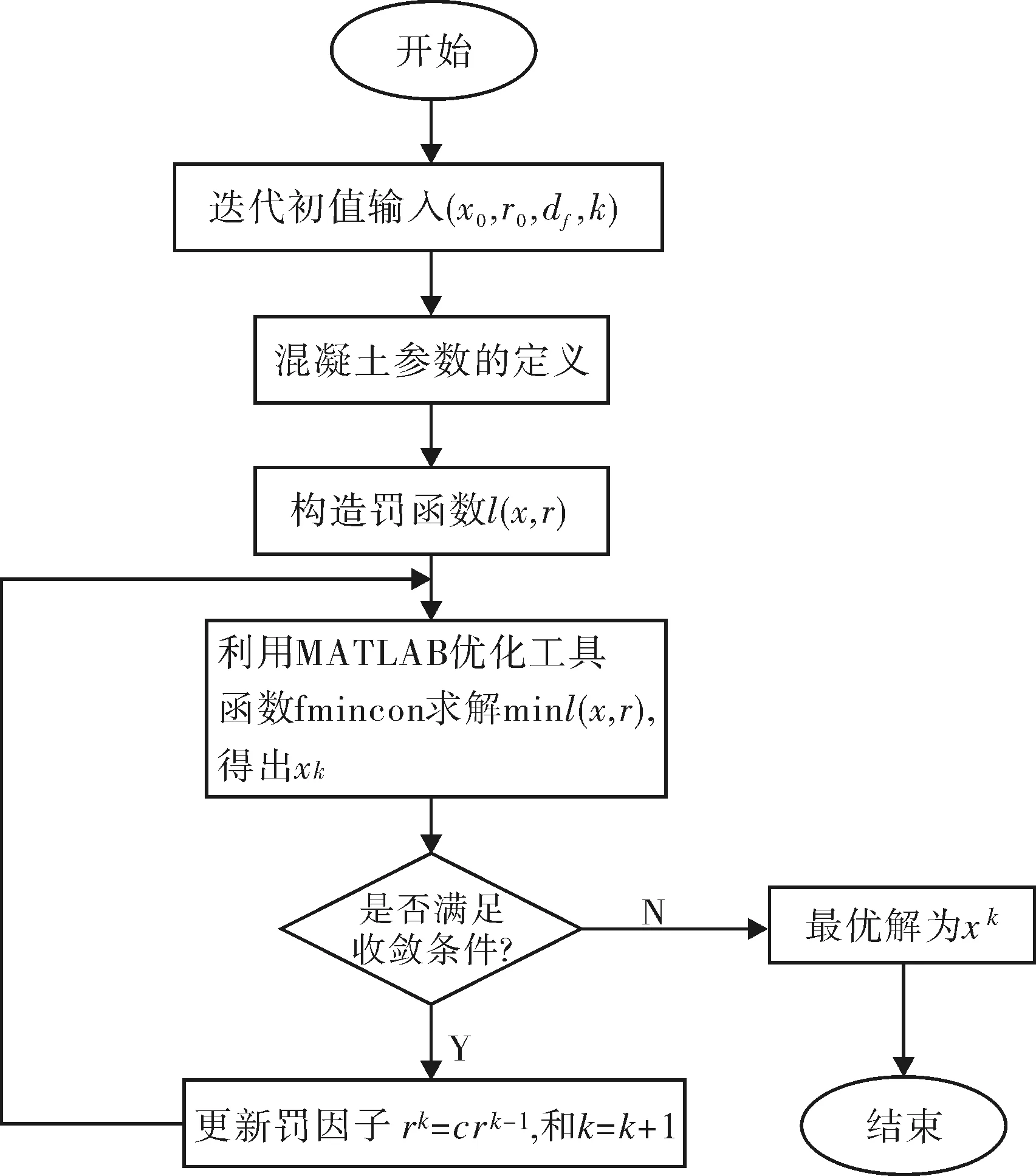
圖2 MATLAB優化實現流程圖Fig.2 MATLAB realize optimization flow chart

4 實例分析

有一矩形截面簡支梁，跨度L=6 m,上面有均布荷載q=50 kN/m作用，其混凝土可選用C20—C40，鋼筋可以選用HRB335,HRB400.材料信息：混凝土單價(C20：400元/m3，C25：415元/m3，C30：430元/m3，C35：445元/m3，C40：460元/m3),鋼筋4 000 元/t.試求在滿足承載力要求及規范所規定的構造要求的條件下，而造價最經濟的設計.

a. 最大彎矩和最大剪力計算

b. 罰函數的構造

φ=(X,r)=450bh+4 000×7.85As-

結果輸出:運用MATLAB優化實現流程，通過10次材料參數的改變，得到各種組合下鋼筋混凝土梁的優化結果如表1所示.

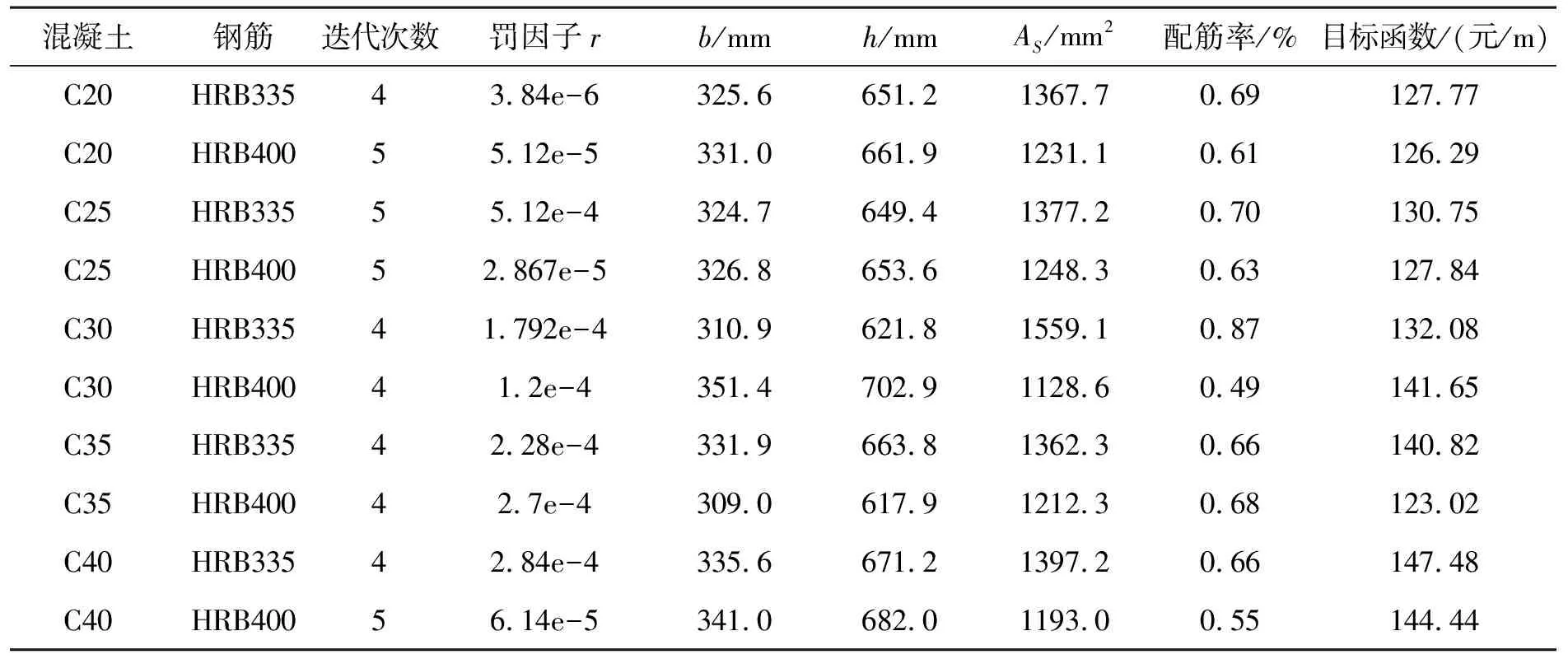
表1 各種組合下的優化結果

5 結 語

a.本文采用了5種混凝土和2種鋼筋進行了組合和比較，最后得出最優的設計方案.從表中可以看出選用C35和HRB400可以作為本設計的最經濟方案.

b.優化設計的結果是否理想和迭代次數的多少，跟選擇的罰因子初值r0有關.如果剛開始選擇了合適的罰因子，迭代次數會大大的減小.

c.從表中可以看出，對于同種混凝土如果適當的增加截面尺寸，而減少鋼筋的用量可以減少結構的造價如：C20,C25,C40；如果增加截面尺寸過大，反而會增加成本如：C30；如果想用減小截面尺寸來減少成本可以通過選用高強度鋼筋的方法如： C35.

d.本設計每個結果都是該組合的最優結果，在約束條件下組合的縱筋最大配筋率為0.87%，在矩形截面梁常用配筋范圍0.6%～1.5%之間.

e.采用MATLAB優化工具箱求解工程優化問題，可以大大的減少工作量，提高優化設計的精度，從而得到最經濟，最有效的設計方案.

參考文獻：

[1] 孫靜. 罰函數法及在鋼筋混凝土梁優化設計中的應用[J]. 山西建筑，2010，36(26):78-79.

[2] 李萬祥.工程優化設計與MATLAB實現[M]. 北京：清華大學出版社，2009.

[3] 蔡新，郭興文，張旭明. 工程結構優化設計[M]. 北京：中國水利水電出版社，2003.

[4] 張靖靜. 鋼筋混凝土受彎構件正截面設計優化設計分析[J]. 工業建筑，2005，35(2):100-102.

[5] 范良宜. 鋼筋混凝土矩形截面梁實用優化設計方法[J]. 基建優化，1998，19(3): 27-30.