基于響應面方法的車輛多目標協同優化

劉士士，谷正氣，伍文廣，米承繼，梁小波，彭國譜

(1. 湖南大學 汽車車身先進設計制造國家重點實驗室，湖南 長沙，410082；2. 湘電重型裝備股份有限公司，湖南 湘潭，411100)

車輛的懸架系統是影響操縱穩定性和行駛平順性的關鍵部件，操縱穩定性和行駛平順性又是評價汽車整體性能的重要指標。近年來，國內外在操縱穩定性和行駛平順性方面已經開展了不少研究[1-8]。然而車輛的操縱穩定性和行駛平順性之間存在著耦合變量，單純基于某一項性能的優化往往會導致另一性能的降低。因此，單目標優化方法或是基于某一性能的多目標優化的方法，未能考慮二者的耦合關系。鑒于此，文中采用一種能同時使車輛的操縱穩定性和行駛平順性達到最佳匹配的協同優化的方法，該方法是一種典型的多學科設計方法，可以將車輛的操縱穩定性和行駛平順性的各項指標進行多目標的平衡和優化。本文作者用ADAMS/CAR軟件建立了完整的整車模型，在優化過程中選用協同優化的響應面算法作為優化方法。響應面方法是在試驗的基礎上考慮其隨機誤差，同時將復雜未知的函數關系在小區域內用簡單的一次或二次多項式來擬合，計算較簡單[9-10]。由于響應面方法是以試驗為基礎，因此，試驗設計的合理性直接影響了優化的準確性和效率，采用中心復合理論進行試驗設計，大大提高了優化效率，使汽車的操縱穩定性和平順性同時得到提高。

1 整車模型的建立和評價指標

本文所研究的模型是在 Adams/CAR軟件中建立的動力學整車模型。該模型共有135個自由度[11]，分為7個子系統，建模時，先分別建立各個子系統的模型，然后在子系統間建立通信端口命令，最后裝配成整車模型。模型的前懸架采用雙橫臂獨立式懸架，后懸架為多連桿獨立懸架，轉向系為齒輪齒條轉向系，制動器為四輪盤式制動器，底盤為去掉車身幾何體的剛性底盤，前后輪胎型號均為 205/50R17。所建的動力學模型如圖1所示，建模中需要的重要參數如表1所示。

鑒于汽車系統的復雜性，建模時進行了如下適當的簡化[12-13]。

(1) 除輪胎、阻尼元件、彈性元件及橡膠元件外，其余構件均作為剛體，忽略其變形；

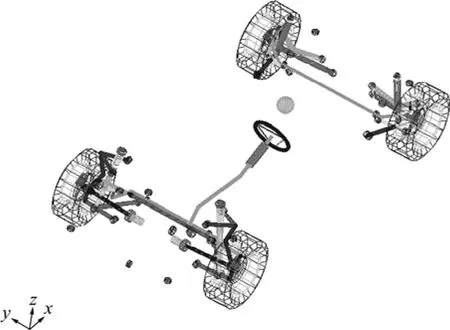
圖1 整車動力學模型Fig.1 Vehicle dynamics model

(2) 對于剛體之間的柔性連接作適當的簡化，用線性彈性橡膠襯套來模擬實際工況下的動力學特性，且對于理想鉸鏈，除轉動副和滑動副之外各運動副的摩擦力均忽略不計。

整車動力學模型建立后，常需要對模型進行試驗驗證，本文采用文獻[1]介紹的方法對該模型進行驗證，驗證結果說明文中的建模方法是可行的，并具有較高的準確度，可以用來進行整車性能預測分析。

汽車的操縱穩定性能是指在駕駛者不感到過分緊張、疲勞的條件下，汽車能遵循駕駛者通過轉向系及轉向車輪給定的方向行駛，且當遭遇外界干擾時，汽車能抵抗干擾而保留穩定行駛的能力。操縱穩定性是影響汽車主動安全的重要性能之一。

汽車操穩性的評價方法很多，一般包括開環和閉環兩種評價方法。在汽車動力學軟件中，操縱穩定性的評價方法可根據中國汽車行業標準 QC/T 480—1999，通過幾種典型的行駛工況來模擬典型駕駛操縱的通道性能，這些典型行駛工況是從汽車實際行駛中選取的，評價比較接近于實際交通情況，因此能如實地反映汽車的操縱穩定性。該標準規定的汽車穩定性的評價指標如下：

表1 整車建模主要參數Table 1 Main parameters of vehicle model

(1) 轉向瞬態響應試驗(轉向盤轉角階躍輸入)仿真試驗按照側向加速度為2 m/s2時的汽車橫擺角速度的響應時間t進行評價計分。汽車橫擺角速度響應時間的評價計分按下式計算：

式中：NJ，t60，t100和t分別為橫擺角速度響應時間的計分值、下限值、上限制和試驗值。

(2) 轉向瞬態響應試驗(轉向角轉角脈沖輸入)仿真試驗按照相位滯后角α進行評價計分。相位滯后角的評價計分按下式計算：

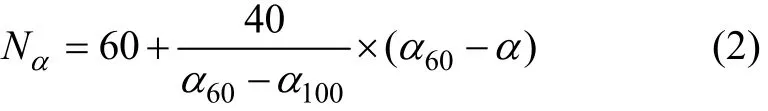
式中：Nα，60α，100α和α分別為相位滯后角的評價計分值、下限值、上限制和試驗值。

(3) 蛇形試驗。仿真試驗按照基準車速(65 km/h)下的平均橫擺角速度峰值γ進行評價計分，平均橫擺角速度峰值的評價計分按下式計算：

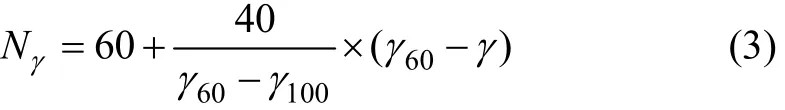
式中：γN，60γ，100γ和γ分別為平均橫擺角速度峰值的計分值、下限值、上限制和試驗值。

(4) 轉向回正試驗。仿真試驗按照松開轉向盤3 s時的殘留橫擺角速度的絕對值rΔ進行評價計分，殘留橫擺角速度的絕對值評價計分按下式計算：

式中：rNΔ，60rΔ，100rΔ和rΔ分別為殘留橫擺角速度絕對的評價計分值、下限值、上限制和試驗值。

汽車平順性主要是保持汽車在行駛過程中產生的振動和沖擊環境對乘員舒適性的影響在一定界限之內，因此平順性主要是根據乘員主觀感覺的舒適性來評價。由于要對所建車型進行多目標的協同優化，考慮操縱穩定性的同時也要考慮平順性，故構建加權加速度均方根值的評價計分值，評價標準同操穩一樣，評價計分值越大越好。行駛平順性隨機輸入試驗評價計分可通過下式計算：

式中：Na，a60，a100和aw分別為隨機輸入試驗的評價計分值、下限值、上限制和試驗值。

2 協同優化的響應面算法

中國汽車行業標準QC/T 480—1999中規定，汽車操縱穩定性的評價按照各項指標的評價計分數大小來衡量，評價計分數小于 60分的為不及格，大于 100分的按照100分來計算。為了便于進行優化，將5個評價指標做如下替換：

所構建的協同優化的系統級數學模型如下：

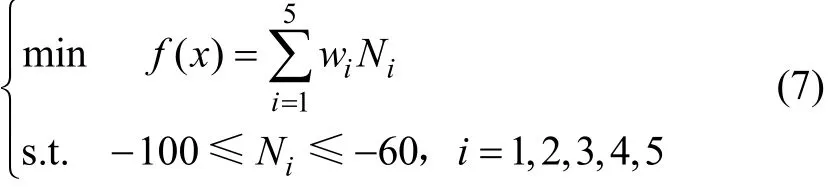
式中：f(x)為多目標的優化函數值；Ni為各個子目標的計分值，可通過仿真試驗獲得；wi為第i項目標函數的權因子，主要表示各子目標函數重要程度。文中進行研究時將 5個子目標函數看作同等重要，所以有wi=1 (i=1, 2, 3, 4, 5)。

懸架系統是影響整車性能的主要因素，而懸架的結構參數和性能參數對汽車的操縱穩定性和行駛平順性有很大的影響。因此，根據文獻[2, 13]，通過影響汽車操縱穩定性和行駛平順性的靈敏度分析，作者把前后懸架的剛度和減震器的阻尼以及橫向穩定桿的扭轉剛度作為操縱穩定性和平順協同優化的變量(假設彈簧和減震器是左右對稱的)。這6個優化變量是對整車的操縱穩定性和行駛平順性影響最大的因素，為了便于仿真計算，將優化變量分別乘以一個比例因子來改變其大小。考慮到文中是在基本確定的模型上進行的優化，所以選定各優化變量的范圍為±50%，設計變量見表2。

文中有優化變量6個，優化目標5個，因此二階響應曲面模型的回歸系數共有。為了得到回歸方程，每個因子所取的水平應大于或等于3，因而所要做的試驗次數是很多的，文中變量有6個，如果做3水平全因子試驗，就需要做729次試驗。而試驗次數之大，很難實現，中心復合試驗設計就是為了解決這一矛盾而提出的一種設計試驗的方法，因此文中選用中心復合設計來設計試驗，并進行回歸設計。作者將各個設計變量正規化，設它們的最大值均為1，最小值均為-1，各個變量具有交互作用。根據文獻[14]經過計算分析，該文需進行32次二水平部分試驗，15次中心點試驗和12次軸向點試驗，共59次試驗。安排好試驗次數，根據1.1節在ADAMS/CAR中建立的整車模型，編寫5個優化目標的驅動控制文件及相應工況的路面進行優化仿真，得到評價指標的計分值。部分試驗安排和仿真結果如表3所示。

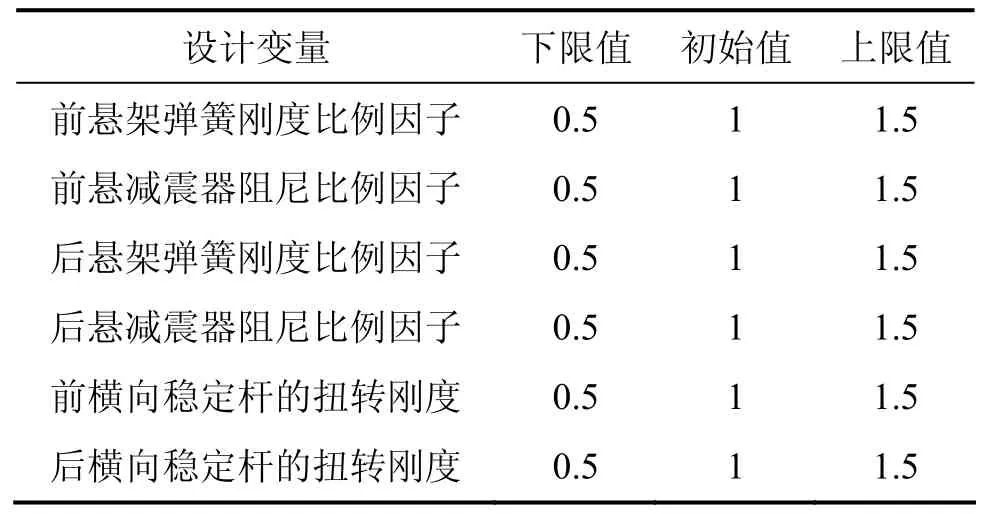
表2 設計變量初始值的取值范圍Table 2 Range of design variables’ initial value

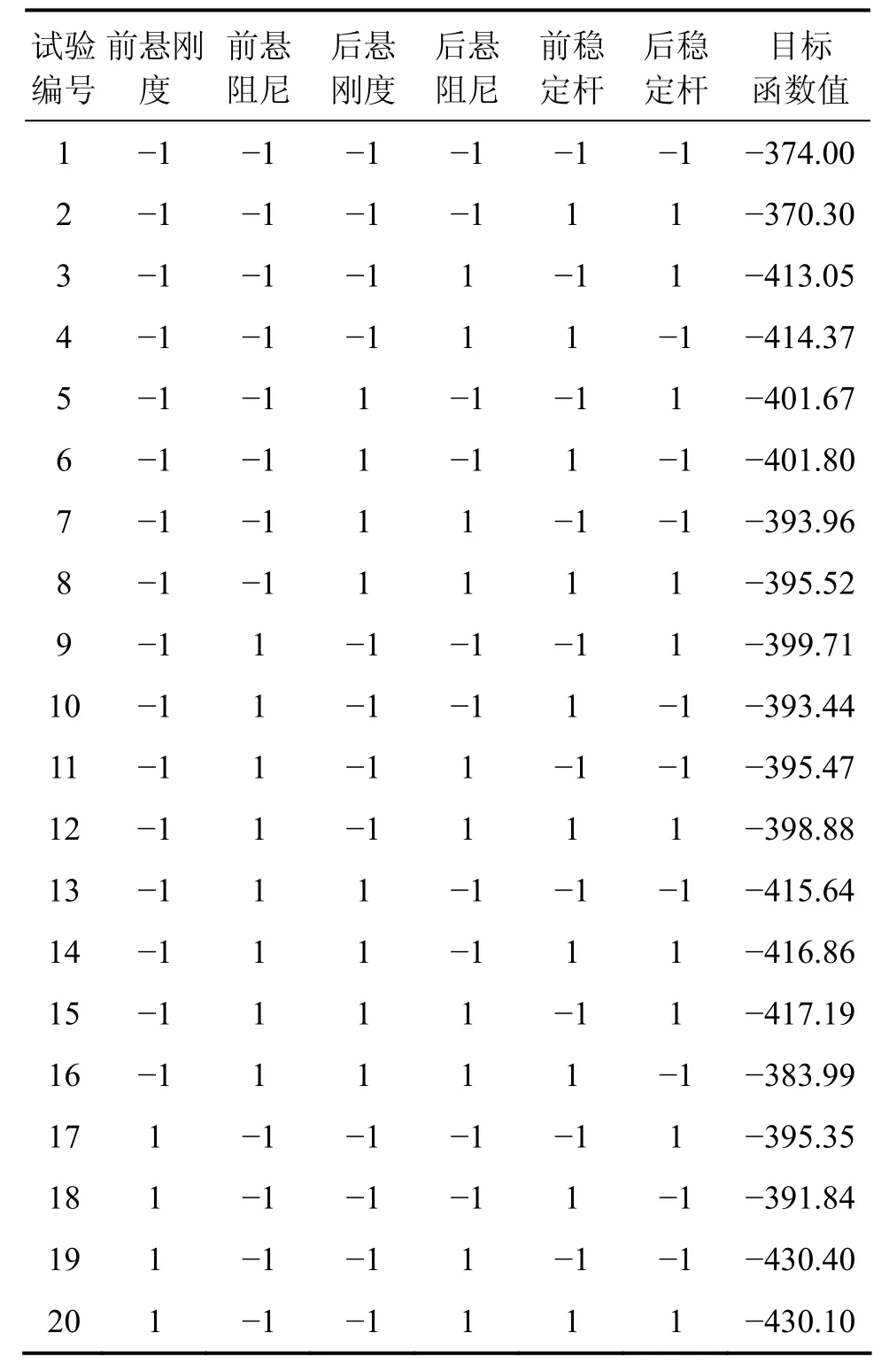
表3 基于中心復合試驗的部分試驗設計Table 3 Part design based on central composite experimental

文中的設計變量有6個，其近似模型見式(8)，其中：ε為隨機誤差，服從正態分布，其均值為零，方差為2σ。

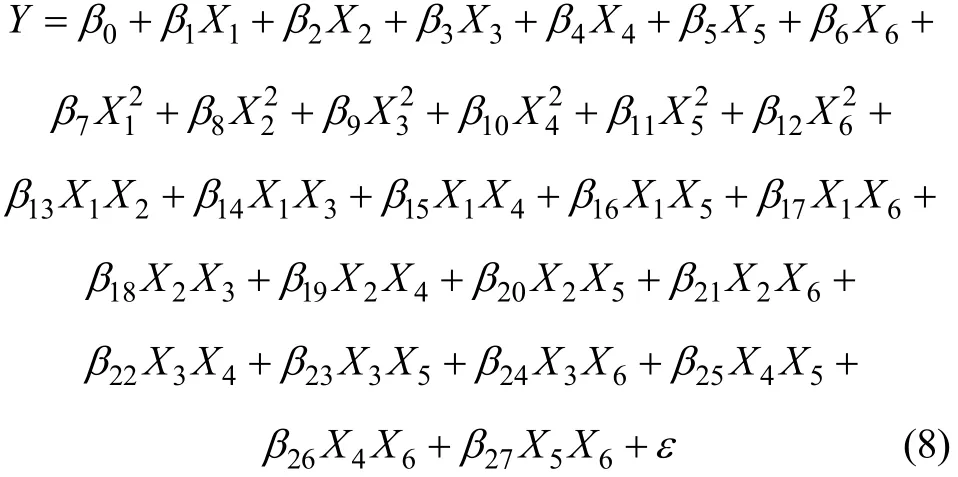
根據實驗結果，獲得在不同變量xi的水平值組合下的系統響應值 yi，用二次多項式模擬作為輸入和輸出的實際函數的近似，根據最小二乘法原理對這些數據進行擬合。

二階響應面的回歸系數β的最小二乘估計值是：

得到回歸模型為：

采用響應面方法進行優化時，需要對擬合的響應面模型進行檢驗。作者采用二階統計模型的顯著性來檢驗該模型參數假設的正確性，計算可得此回歸模型的回歸平方和、誤差平方和以及檢驗統計量等，表 4所示為顯著性方差分析參數表。

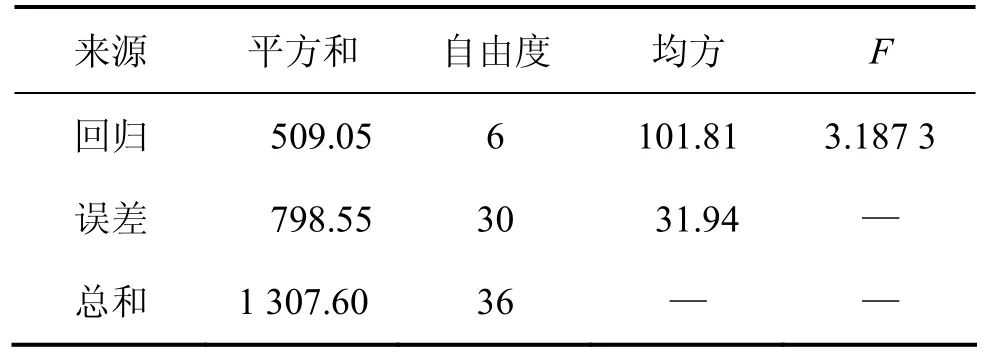
表4 顯著性方差分析Table 4 Significant analysis of variance

查表可得 F0.1,6,30=2.61，由于 F0.1,6,30＜F，因此該統計模型在顯著性水平10%下是顯著的，即該模型能較好地擬合仿真試驗數據。

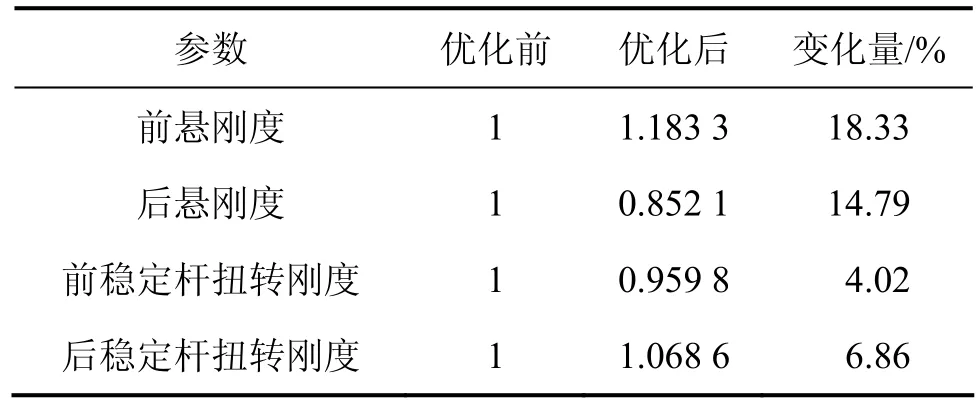
表5 優化前后參數變化量對比Table 5 Parameter variation compared before and after optimization

3 優化結果

通過擬合得出二次目標函數，運用 MATLAB優化工具箱對目標函數在可行域內進行優化，使該函數取得最小值[15]，圖2和3所示為變量優化前后的阻尼曲線，表5所示為其數值變化，圖4～8所示為試驗中評價操縱穩定性和平順性的性能曲線，表6所示為評價分。

圖2 優化前后前懸架阻尼曲線Fig.2 Front suspension damping curves before and after optimization

圖3 優化前后后懸架阻尼曲線Fig.3 Rear suspension damping curves before and after optimization

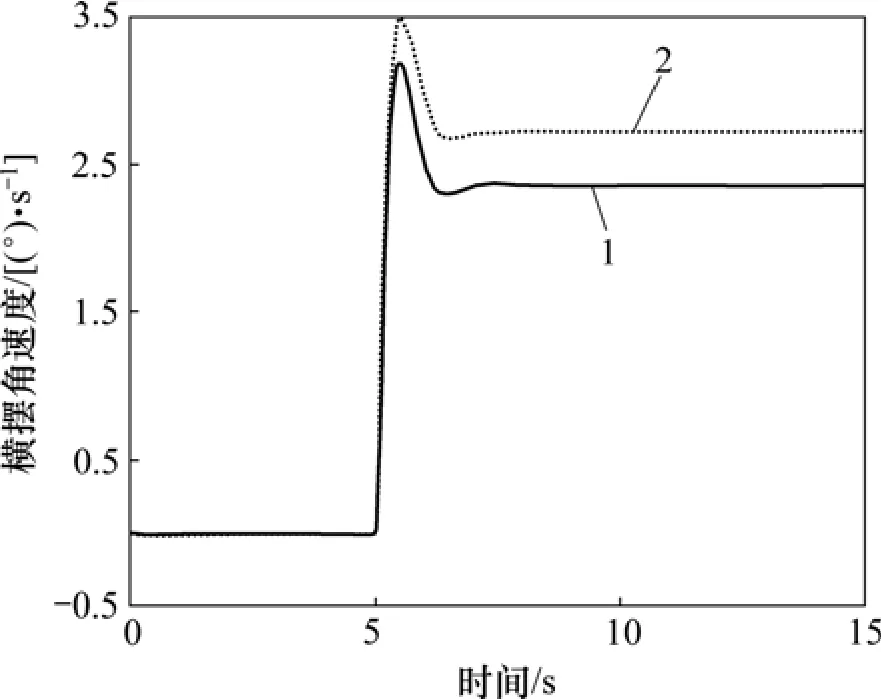
圖4 優化前后轉向盤角階躍輸入試驗中橫擺角速度曲線Fig.4 Yaw rate curves of step input of steering wheel angle experiments before and after optimization

圖5 優化前后轉向角轉角脈沖試驗中橫擺角速度曲線Fig.5 Yaw rate curves of angle pulse of steering wheel angle before and after optimization

從仿真結果及其優化前后仿真圖形對比可以看出，優化后操縱穩定性中的橫擺角速度響應時間縮短，超調量也相應減少；平順性性能中的車身質心位置的加權加速度均方根值比優化前減少5%左右。文中所采用的優化方法使汽車總的評價指標的計分提高了13%，操縱穩定性和平順性同時得到優化。

圖6 優化前后蛇行試驗中橫擺角速度曲線Fig.6 Yaw rate curves of hunting test before and after optimization

圖7 優化前后轉向回正試驗中橫擺角速度曲線Fig.7 Yaw rate curves of steer-return test before and after optimization

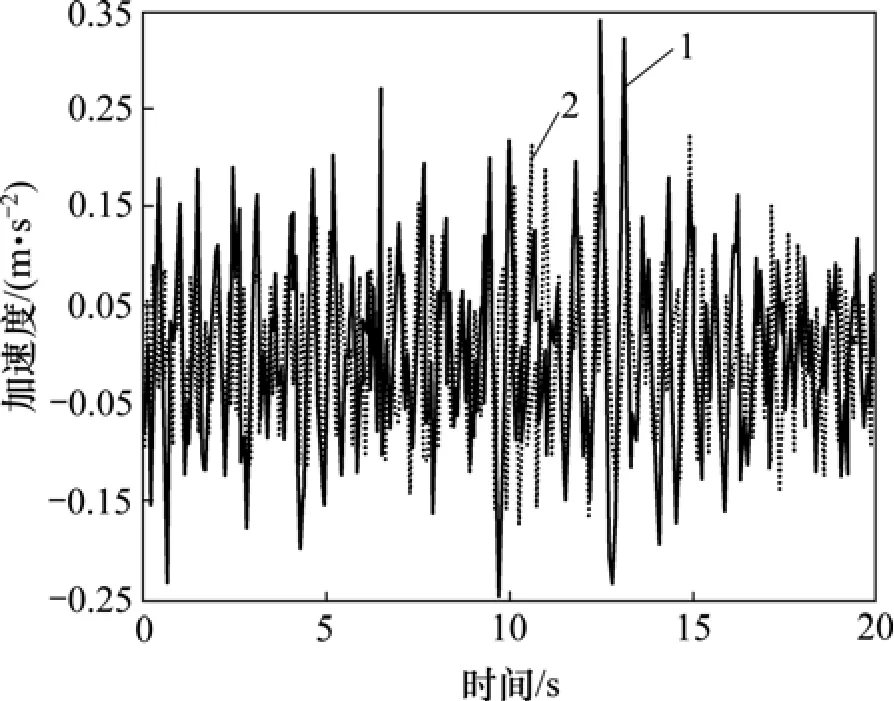
圖8 優化前后平順性B級隨機路面車身垂向加速度曲線Fig.8 Vertical acceleration of vehicle body curves of comfort test in B-class random road

表6 優化前后評價分變化量Table 6 Evaluation of changes in scores before and after optimization

4 結論

(1) 利用ADAMS/CAR軟件建立整車剛柔耦合多體系統動力學模型，并運用中心復合實驗設計理論，結合響應面方法擬合出二次響應面模型，得到的最優解使車輛的操縱穩定性和平順性性能同時得到提高。

(2) 將協同優化的響應面算法用在整車操縱穩定性和平順性優化中，所涉及的變量的選擇和優化方法對其他類型車輛的設計和車輛其他性能的協同優化同樣具有一定的參考價值。

[1] 海貴春. 某智能四驅SUV動力學性能分析與優化研究[D]. 長沙: 湖南大學機械與動載工程學院, 2008: 37-116.HAI Gui-chun. Analysis and optimization of dynamic performance for a SUV[D]. Changsha: Hunan University.School of Mechanical and Vehicle Engineering, 2008: 37-116.

[2] 呂征, 谷正氣, 李偉平, 等. 基于響應面方法的汽車操縱穩定性優化[J]. 系統仿真學報, 2009, 21(24): 7961-7968.Lü Zheng, GU Zheng-qi, LI Wei-ping, et al. Optimization of vehicle handing and stability based on RSM[J]. Journal of System Simulation, 2009, 21(24): 7961-7968.

[3] Sobieski J S, Kodiyalam S, Yang R Y. Optimization of car body under constrains of noise, vibration, and harshness(NVH), and crash[J]. Structural and Multidisciplinary Optimization, 2001,22(4): 295-306.

[4] Uys P E. Criteria for handling measurement[J]. Journal of Terramechanics, 2006, 43: 43-67.

[5] Uys P E. Suspension settings for optimal ride comfort of off-road vehicles traveling on roads with different roughness and speeds[J]. Journal of Terramechanics, 2006, 18: 1-13.

[6] Craig K, Stander N, Dooge D, et al. MDO of automotive vehicle for crashworthiness and NVH using response surface methods[C]//The 9th AIAA/ISSMO Symposium on Multidisciplinary Analysis and Optimization. 2002:AIAA-2002-5607.

[7] 鄭軍. 新概念車操縱穩定性與舒適性研究[D]. 長沙: 湖南大學機械與運載工程學院, 2007: 52-110.ZHENG Jun. On the ride comfort and handling characteristics of a new concept car[D]. Changsha: Hunan University. School of Mechanical and Vehicle Engineering, 2007: 52-110.

[8] 楊榮山, 袁仲榮, 黃向東, 等. 基于近似模型的車輛操縱穩定性及平順性的優化研究[J]. 汽車技術, 2009(7): 18-22.YANG Rong-shan, YUAN Zhong-rong, HUANG Xiang-dong,et al. Optimization and research on vehicle’s handling stability and ride comfort based on approximate model[J]. Automobile Technology, 2009(7): 18-22.

[9] 王婭, 谷正氣, 李偉平, 等. 基于響應面方法的某智能 SUV平順性優化[J]. 機械科學與技術, 2010, 29(3): 373-379.WANG Ya, GU Zheng-qi, LI Wei-ping, et al. Optimization of the ride comfort of an intelligent sport-utility vehicle(SUV)[J].Mechanical Science and Technology for Aerospace Engineering,2010, 29(3): 373-379.

[10] 陳立周. 機械優化設計方法[M]. 北京: 冶金工業出版社,2005: 215-230.CHEN Li-zhou. Mechanical optimum design[M]. Beijing:Metallurgical Industry Press, 2005: 215-230.

[11] 海貴春, 谷正氣, 駱軍, 等. 某 SUV 車穩態轉向特性與優化[J]. 系統仿真學報, 2009, 21(7): 2068-2071.HAI Gui-chun, GU Zheng-qi, LUO Jun, et al. Analysis and optimization of stable steering characteristic for SUV[J]. Journal of System Simulation, 2009, 21(7): 2068-2071.

[12] 陳黎卿, 陳無畏. 基于聯合仿真技術的主動懸架自適應模糊PID控制研究[J]. 系統仿真學報, 2008, 20(5): 1340-1344.CHEN Li-qing, CHEN Wu-wei. Study of active suspension adaptive fuzzy control based on co-simulation[J]. Journal of System Simulation, 2008, 20(5): 1340-1344.

[13] 王凱峰. 基于虛擬現實與虛擬樣機的汽車操縱穩定性研究[D].合肥: 合肥工業大學機械與汽車工程學院, 2007: 28-29.WANG Kai-feng. Research on vehicle handling stability based on virtual reality and virtual prototype[D]. Hefei: Hefei University of Technology. School of Mechanical and Automotive Engineering, 2007: 28-29.

[14] 任露泉. 試驗優化設計與分析[M]. 2版. 北京: 高等教育出版社, 2003: 246-278.REN Lu-quan. Optimum design and analysis of experiments[M].2nd ed. Beijing: Higher Education Press, 2003: 246-278.

[15] 蘇金明, 阮沈勇, 王永利. Matlab工程數學[M]. 北京: 電子工業出版社, 2005: 73-83.SU Jin-ming, RUAN Shen-yong, WANG Yong-li. Matlab engineering mathematics[M]. Beijing: Electronic Industry Press,2005: 73-83.