對稱協同開采人工礦柱失穩的突變理論分析

陳慶發，古德生，周科平，蘇家紅

(1. 中南大學 資源與安全工程學院，湖南 長沙，410083；2. 廣西大學 資源與冶金學院，廣西 南寧，530004；3. 廣西華錫集團股份有限公司，廣西 柳州，545006)

隨著全球對礦產資源的爭奪進一步升級，原本不太引人注意的采空區隱患資源也日益受到關注。據不完全統計，這部分資源目前已經占我國有色金屬資源的1/3，將成為我國礦業發展的重要接替資源[1]。傳統觀念認為資源開采與空區治理一種矛盾，分別獨立設計、施工。本文作者從礦山大系統角度出發，以采礦環境再造理論[2-3]為指導，引入協同論，提出了“隱患資源開采與采空區處理協同”的礦業發展新技術模式及“協同利用”采空區處理新方法[4]。人工礦柱支撐頂板是采空區協同利用的基本模式之一，其與頂板之間的變形協調機制與礦石礦柱的相比有明顯差別，研究人工礦柱的穩定性對于采空區周邊隱患資源的協同開采起著至關重要的作用。對礦柱的穩定性分析，已從單一的強度理論、經驗公式，向圍巖組成的力學平衡系統的失穩研究方向發展。秦四清等[5-6]應用突變理論分析了對稱開采時的礦柱失穩效應；李江騰等[7-8]對與非對稱開采的礦柱失穩的突變模型進行探討。本文作者基于突變理論，探討對稱協同開采時人工礦柱突發失穩的力學機理。

1 頂板-人工礦柱的協同作用模型及變形協調機制

人工礦柱形成前，頂板已經發生一定程度的下沉，在未發生突發失穩前，實施人工礦柱支撐措施，一方面，可抑制頂板后期下沉，避免可能的災害事故；另一方面，留設的部分空間可作為資源開采過程中的部分空間進行利用(如爆破補償空間)，實現隱患資源開采與空區處理的協同。

人工礦柱的空間表現形式有很多種，其中長條形人工礦柱最常見。根據材料力學，為簡化分析，可將空區頂板視為彈性梁。為了達到最佳抑止效果，人工礦柱應布設于空區中間，荷載通過頂梁傳遞給人工礦柱。由于礦柱相對狹窄，單位長度的礦柱的作用視為作用在梁跨中的集中力 F，巖梁自重和上覆巖層的作用簡化為均布載荷 q。在頂板未發生突發失穩前，對于硬巖來說，人工礦柱的變形遠大于采空區周邊圍巖的變形，故認為梁是固支的。

根據前述分析，分別繪出采空區頂板-人工礦柱組合結構示意圖及采空區頂板-人工礦柱協同作用力學模型[9-10]分別見圖1和圖2。

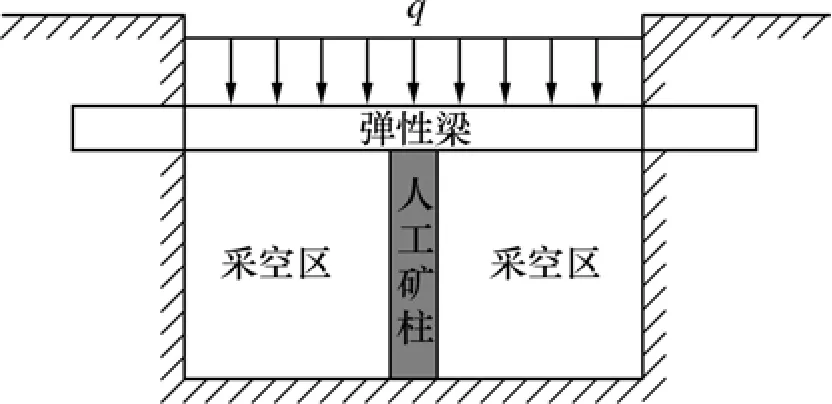
圖1 頂板-人工礦柱組合結構Fig.1 Composite structure of roof-artificial pillar

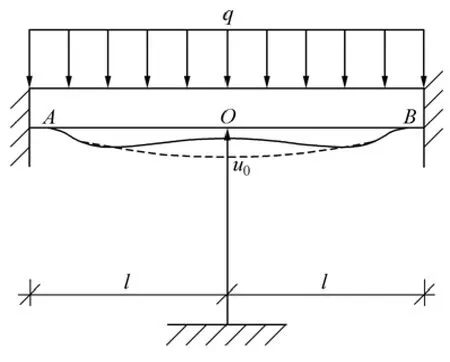
圖2 頂板-人工礦柱協同作用力學模型Fig.2 Synergistic effect mechanical model of roof-artificial pillar

根據損傷力學，人工礦柱的應力和應變關系可用weibull分布模型表達為[11]：

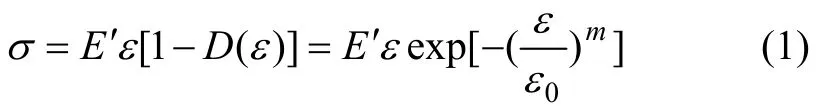
式中：σ和E′分布為人工礦柱膠結充填體的應力與彈性模量；ε0為平均應變測度；m為分布函數的形狀參數，其物理意義反映了介質的均質性，定義為介質的均勻性系數。

對于上述協同作用力學模型，若梁和人工礦柱長度方向取1個單位，則寬度為d、高度為h的人工礦柱在被壓縮量為u′時，有：

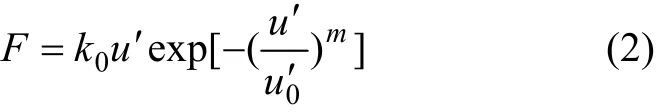
根據材料力學理論，無集中力F作用時，彈性梁達到圖2虛線所示的靜平衡位置，此時，考慮人工礦柱集中力F作用時，彈性量的部分能量釋放在人工礦柱上，頂板彈性梁AO的彎距方程有：

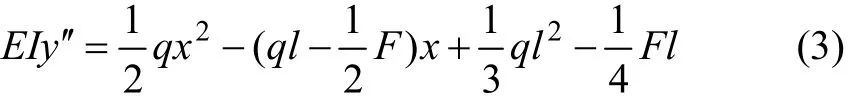
根據邊界條件：

對式(3)積分，可得AO段的撓曲線方程：

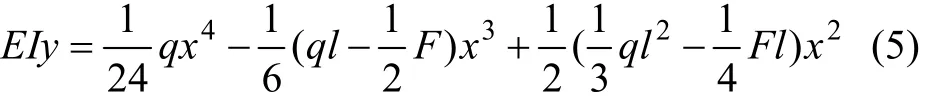
當x=l時，將y(l)=u0-u′代入撓曲線方程，可以得出人工礦柱壓縮量關系式：

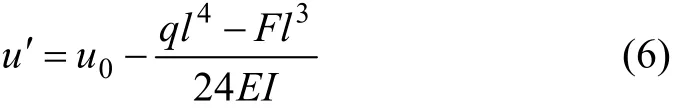
可見：人工礦柱壓縮量是1個依賴于頂板彈性模量、泊松比、覆巖和頂板自重、頂板慣性距、采空區寬度、膠結充填體隔墻的彈性模量、寬度和高度等參數有關的量。

2 人工礦柱失穩的尖點突變模型

2.1 突變理論

1972年Thom創立并系統闡述了突變理論[12]，之后許多學者對該理論進行了研究，其中最有影響的是Zeeman提出的“突變理論”[13]。

突變理論認為，系統所處的狀態可以用一組參數描述。當系統穩定時，標志該狀態的某一函數就有唯一的取值。當參數在某一范圍變化時，該函數有多個極值，系統處于不穩定狀態。隨著參數的繼續變化，系統又從不穩定態進入另一穩定態，此時，系統就會發生突變。可以在不知道系統有哪些微分方程且不需求解微分方程的條件下，僅在幾個假設的基礎上，用少數幾個控制變量便可以定性或定量地預測系統的性質。

由分類定理對梯度系統進行分類后指出：在控制變量不大于4個時，有7種初等突變形式(折疊、尖點、燕尾、蝴蝶、雙曲點、橢圓臍點和拋物臍點)。目前，除個別情況，大多數研究者將問題歸結為尖點突變模型去處理，如：施澤進等[14]建立了斷層活動的尖點突變模型；黃潤秋[15]建立了反傾斜坡彎曲拉裂的尖點突變模型；劉軍等[16]通過綜合考慮了地下水的影響建立了一個新的巖體失穩尖點突變模型。

2.2 人工礦柱失穩的尖點突變模型

尖點突變模型勢能函數標準形式為：

式中：x為狀態變量；u和v為控制變量。

相空間由狀態變量x及控制變量u和v構成的三維空間。相空間平衡曲面 M 方程可通過對勢能函數V(x)求導得到：

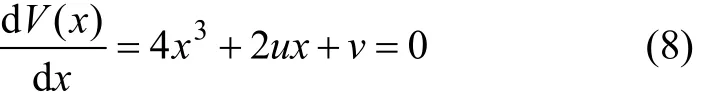
相空間中的圖形稱為突變流形，它是1個有褶皺的曲面，從而在不同的區域內，平衡位置為 1個、2個或3個。對應于中葉的勢函數取極大值，平衡位置是不穩定的；而對應于上下葉的平衡位置上是穩定的。顯然，在曲面有豎直切線，即滿足：

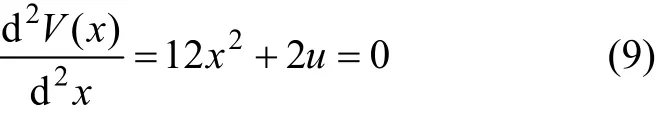
由式(9)可見：平衡位置的數目是不同的，這些點稱為突變點或奇異點，實際上是曲線的拐點，是1條拋物線，如圖3所示。

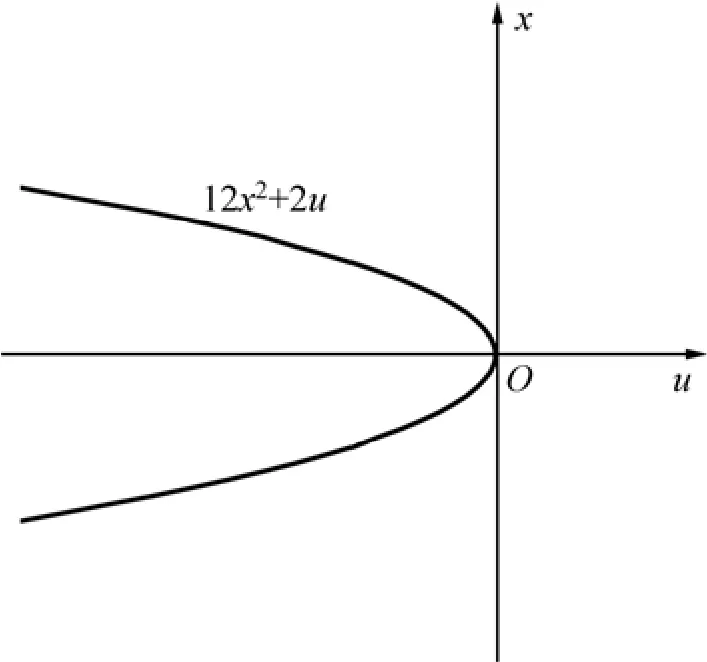
圖3 勢函數二階導數為零的拋物線Fig.3 Parabolic at potential function’s second derivative zero

由式(8)和(9)消去x，可得到滿足分支點集的方程：

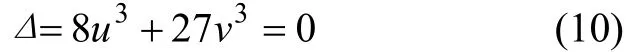
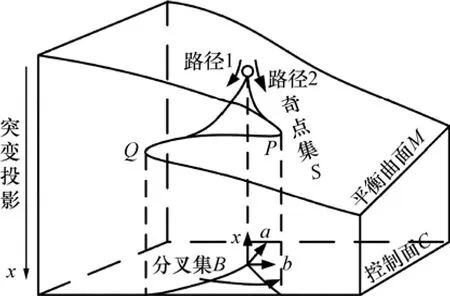
圖4 尖點突變模型圖Fig.4 Cusp catastrophe model diagram

平衡狀態曲面由上、中、下3葉組成，如圖4所示。從正面看，其形態似1條S形曲線，存在明顯的拐點。設想系統的狀態是以(x，u，v)為坐標的三維相空間的1點來表示，任一相點必然落在三葉曲面上。當系統參數發生變化時，它經歷的平衡位置是突變流形上的1條曲線，這樣，就可以分析由1個光滑的勢函數所控制的系統中如何會出現不連續的性態。

由式(2)和(10)，根據靜力平衡條件，可以得到總勢能的一階導數，即有突變流形方程：

根據平衡曲面的光滑性質，求得尖點。尖點處有V″=0，得到：

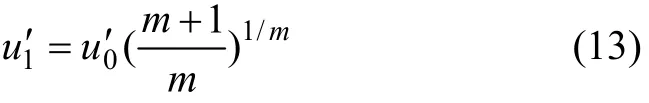
即尖點處在人工礦柱本構關系曲線拐點處。

將平衡曲面方程相對于1u′用Tayloy展開式展開，截取至3次項，然后，修改為尖點突變模型的平衡曲面標準形式4x3+2ux+v=0得：

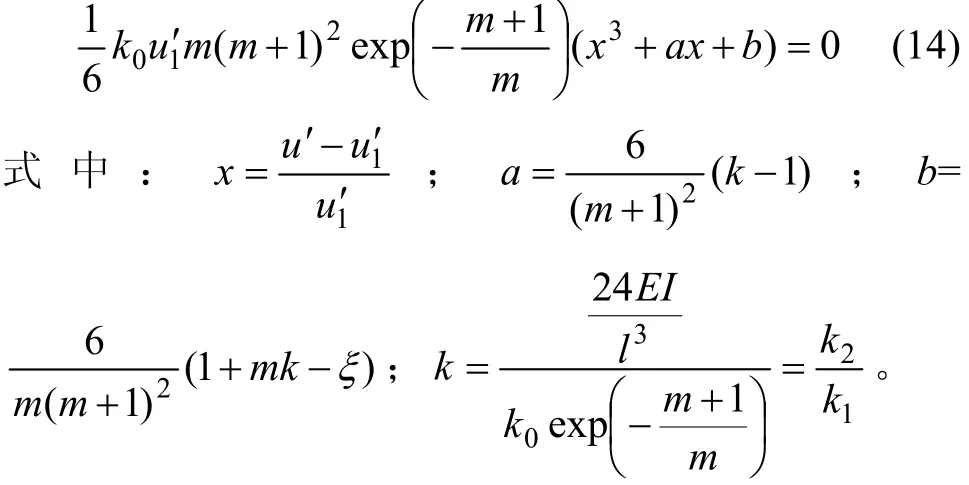
按尖點突變模型逐步進行推導，最終得到系統發生失穩的充要條件：

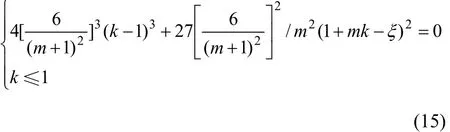
可見：系統突發失穩與系統剛度比有密切相關性；當系統的各部分的彈性模量、采空區寬度和人工礦柱的幾何參數和力學性質參數等沒有發生變化時，k隨m的增大而減小。

3 人工礦柱對頂板穩定性調控作用

在m不變時，人工礦柱充填體的力學參數和幾何參數是可以根據需要進行調控的，即的。

充填體的彈性模量E′可通過改變混凝土各項配比在一定范圍內實現調整，必要時可能采用化學藥劑進行調整。

在m和混凝土質量已確定的情況下(即E′確定)，人工礦柱的高度h對應于采空區的高度，加大礦柱寬度來強化其支撐能力，從而強化頂板的穩定性。

根據剛度比小于等于1的特性，施工中，人工礦柱的寬度必須滿足如下公式：

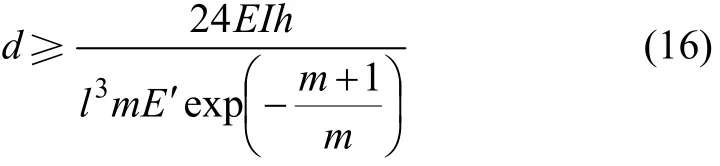
實施人工礦柱后的采空區剩余空間寬度，可根據采礦工藝對各種空間的要求進行留設，一般來說，爆破補償空間不低于2 m，各種機械設備用硐室按規程而定(一般大于2 m)。

此外，采空區在人工礦柱有最小必要寬度后，無需形成更寬的人工礦柱，必要時可在剩余空間內通過充填采場廢石進一步強化人工礦柱的支撐能力，調整采空區局地應力環境。

4 結論

(1) 通過分析實施人工礦柱工藝前后頂板力學狀態的變化規律，建立了頂板-人工礦柱協同作用力學模型，分析了組合結構變形協調機制，推導了人工礦柱的壓縮量表達式。

(2) 基于突變理論，建立了人工礦柱突發失穩的尖點突變模型。人工礦柱突發失穩與剛度比 k、介質均勻性系數m具有密切相關性。

(3) 通過改變人工礦柱的力學參數和幾何參數，可在一定程度上調控頂板的穩定性和采空區局地應力環境，為協同開采隱患資源服務。

[1] 鄒國良. 我國有色金屬危機礦山發展對策[J]. 金屬礦山, 2007,36(12): 22-23.ZOU Guo-liang. Countermeasures for development of China’s non-ferrous metallic mines in crisis[J]. Metal Mine, 2007, 36(12):22-23.

[2] 古德生, 李夕兵. 現代金屬礦床開采科學技術[M]. 北京: 冶金工業出版社, 2006: 66-86.GU De-sheng, LI Xi-bing. Modern mining science and technology for metal mineral resources[M].Beijing:Metallurgical Industry Press, 2006: 66-86.

[3] 周科平, 高峰, 古德生. 采礦環境再造與礦業發展新思路[J].中國礦業, 2007, 16(4): 34-36.ZHOU Ke-ping, GAO Feng, GU De-sheng. Mining environment regenerating and new thoughts on the development of mining industry[J]. China Mining Magazine, 2007, 16(4): 34-36.

[4] 陳慶發, 周科平, 胡建華, 等. 碎裂礦段開采與空區處理協同研究[J]. 中南大學學報: 自然科學版, 2010, 41(2): 728-735.CHEN Qing-fa, ZHOU Ke-ping, HU Jian-hua, et al. Synergism study of mining and goaf treatment in cataclastic ore section[J].Journal of Central South University: Science and Technology,2010, 41(2): 728-735.

[5] 秦四清, 何懷鋒. 狹窄煤柱沖擊地壓的突變理論分析[J]. 水文地質與工程地質, 1995, 18(5): 17-20.QIN Si-qing, HE Huai-feng. Analysis of the destabilization for the narrow coal pillar burst by the catastrophe theory[J].Hydrogeology and Engineering Geology, 1995, 18(5): 17-20.

[6] 徐曾和, 徐小荷, 唐春安. 堅硬頂板下煤柱巖爆的尖點突變理論分析[J]. 煤炭學報, 1995, 20(5): 485-491.XU Zeng-he, XU Xiao-he, TANG Chun-an. Theoretical analysis of a cusp catastrophe bump of a coal pillar under hard rocks[J].Journal of China Coal Society, 1995, 20(5): 485-491.

[7] 李江騰, 曹平. 非對稱開采時礦柱失穩的尖點突變模型[J].應用數學和力學, 2005, 26(8): 1003-1008.LI Jiang-teng, CAO Ping. Cusp catastrophe model of instability of pillar in asymmetric mining[J]. Applied Mathematics and Mechanic, 2005, 26(8): 1003-1008.

[8] 潘岳, 張勇, 吳敏應, 等. 非對稱開采礦柱失穩的突變理論分析[J]. 巖石力學與工程學報, 2006, 25(Suppl.2): 3694-3702.PAN Yue, ZHANG Yong, WU Min-ying, et al. Analysis of catastrophe theory for pillar destabilization in dissymmetric mining[J]. Chinese Journal of Rock Mechanics and Engineering,2006, 25(Suppl.2): 3694-3702.

[9] 潘岳, 王志強, 張勇. 突變理論在巖體系統動力失穩的應用[M]. 北京: 科學出版社, 2008: 87-93.PAN YUE, WANG Zhi-qing, ZHANG Yong. Application of catastrophe theory for dynamic failure of rock[M]. Beijing:Science Press, 2008: 87-93.

[10] 秦四清, 王思敬. 煤柱-頂板協同作用的脆性失穩與非線性演化機制[J]. 工程地質學報, 2005, 13(4): 437-446.QIN Si-qing, WANG Si-jing. Brittle instability and non-linear evolution mechanism of the synergistic action of pillar roof system[J]. Journal of Engineering Geology, 2005, 13(4):437-446.

[11] Karcinovic D. Statistic aspects of the continuous damage theory[J]. Int.J Soils Structure, 1999, 18(7): 551-962.

[12] Thom R. Structural stability and morphs genesis [M]. New York:Benjamin Addison Wesley, 1997: 1-28.

[13] Zeeman E C. Catastrophe theory[J]. Scientific American, 1976,236(4): 65-83.

[14] 施澤進, 羅蟄潭, 彭大鈞. 非線性地質勘探研究導論[M]. 成都: 四川科學技術出版社, 1995: 40-55.SHI Ze-jin, LUO Zhe-tang, PENG Da-jun. Introduction to nonlinear geological prospecting[M]. Chengdu: Sichuan Science and Technology Press, 1995: 40-55.

[15] 黃潤秋, 許強. 工程地質廣義系統科學分析原理及應用[M].北京: 地質出版社, 1997: 139-143.HUANG Run-qiu, XU Qiang. Theory and application of generalized systemic science analysis in engineering geology[M].Beijing: Geology Press, 1997: 139-143.

[16] 劉軍, 秦四清, 張倬元. 緩傾角層狀巖體失穩的尖點突變模型研究[J]. 巖土工程學報, 2001, 23(1): 42-44.LIU Jun, QIN Si-qing, ZHANG Zhuo-yuan. Study on cata strophic model with cusp point for failure of stratified rock mass with a gentle inclination[J]. Chinese Journal of Geotechnical Engineering, 2001, 23(1): 42-44.