公交停靠站通行能力及泊位數設計研究
楊 波,瞿春濤
(1.成都市規劃設計研究院,四川成都 610081;2.中國華西工程設計建設有限公司,四川成都 610031)
公交停靠站作為公交系統的節點,是乘客與公交系統連接的橋梁。而公交停靠站的通行能力又決定了公交線路通行能力,決定了停靠站的設計尺寸,即停靠站的泊位數。合理的泊位數又決定了站點的利用情況:停靠站的泊位數設計過少,站長過短,導致公交車輛頻繁地在站外等候進站,增加了公交車輛的運行時間,而且對道路交通流產生不利的影響;停靠站的泊位數設計過多,站長過長,則增加了車輛在站臺的運行時間,停靠站不能有效利用。所以停靠站的通行能力和泊位數設計具有重要的研究價值。
李娜,陳學武[1]分析了影響停靠能力的四個因素:在站消耗時間,公交車到達率,站長和道路交通狀況,利用回歸分析的方法確定了合理的站長。王波[2]對公交專用道上停靠站停車位的計算方法進行了研究,重點針對隨機性到達情況,文章運用排隊論和引入置信度提出計算模型,并通過示例說明該方法的計算過程。
本文主要依據《公交通行能力和服務水平手冊(第二版)》[3],探討了公交停靠站通行能力模型中相關參數值的確定方法,根據采集的基礎數據,利用仿真軟件對清空時間和有效泊位數進行研究。利用通行能力分析和排隊論兩種方法計算停靠站的泊位數,運用實例探討這兩種方法的應用情況。
1 公交停靠站通行能力分析
公交停靠站的通行能力是指對于某一公共汽車停靠站而言,在一定的道路交通狀況下,在同一時間內所能服務停靠的最多車輛數。停靠能力是一個反映公交車中途停靠站提供為公交車停靠的服務能力大小的指標,是公交設施提供公交服務的供應量。設計泊位數必須達到停靠站所能提供最大停靠能力的要求。停靠站的通行能力主要取決于公交車輛的站點停靠時間和停靠站的類型、泊位數、站長、臨道交通量等等。單個泊位的停靠站通行能力計算公式為[3]如下。
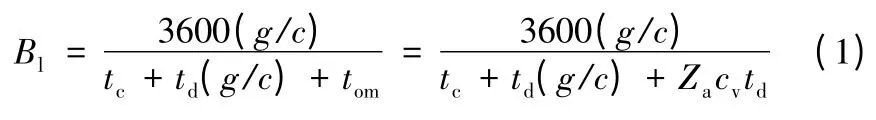
式中:Bl為單個停靠泊位的通行能力(輛/h);g/c為綠信比(等于1.0 就代表了無信號交叉口的狀況);tc為清空時間(s),包括車輛啟動時間(2~5 s)、駛出一個公交車長的時間(5~10 s)、重新匯入車流的延誤時間;td為平均停靠時間;tom為運行裕量;Za為期望失敗率a 對應的標準正態分布值;cv為停靠時間的變異系數。
1.1 清空時間分析
從車輛關門到駛離站點,這段時間為清空時間tc。當后面車輛不能匯入超越前車進站時,即車輛排隊進站時,這段時間是固定的,包括車輛啟動時間、行駛自身長度時間、離開站臺時間。多項研究[3]得出清空時間為9~20 s 之間。車輛啟動-行駛自身長度-駛離車站需要10 s 左右的時間。
當車輛在港灣式停靠站停靠的時候,清空時間將會包含另外一個時間:公交車輛等待進入臨近車道的時間,即公交車輛重新進入車道產生的延誤時間。這個時間取決于相鄰車道的交通流量,隨著流量增加而增加。同時取決于上游交叉口的交通信號,將會產生較大的間隙,車流連續通過站點。可以使其他車輛讓行公交車進入行車道,以減少或者消除延誤(圖1)。
由于車輛隨機到達,且受到控制方式的影響,港灣式車站的公交車重新進入車道的延誤時間可以采用仿真的辦法進行研究。現利用VISSIM 交通仿真軟件進行仿真試驗,本試驗主要模擬遠端停靠站的車輛行為,研究車輛匯入車流時產生的延誤時間。根據高峰時間實際公交車輛到達情況,輸入公交到達和停靠的基本參數,以及駕駛員駕駛特征參數(車輛跟馳、換道以及優先規則等等),在不同的臨道交通量和交通控制方式下進行交通仿真。臨道交通量取100~1000(輛/h),控制方式分為信號控制(g/c=0.5)和無信號控制(g/c=1.0)進行多組試驗。

圖1 港灣式停靠站車輛運行示意

圖2 臨道交通量與延誤時間關系
由圖2可以看出:隨著臨道交通量的增加,延誤時間也隨之增加;上游有信號控制的條件下,公交車輛可以利用信號控制產生的間隙進入車道,延誤時間比無信號控制的延誤時間相對較小;仿真結果值與手冊建議的的延誤時間值相差不大。
1.2 有效泊位數分析
停靠泊位越多,公交停靠站通行能力越大,因為更多的公交車輛可以同時上下客。每增加一個停靠站所增加的停靠能力,取決于停靠泊位是港灣式還是直接式的,以及車輛到達特征。但是停靠站通行能力隨著泊位數的增加并不是線性增長的,所以研究物理泊位的有效性具有重要的實際意義。
現通過交通仿真的辦法確定停靠站泊位的有效性。VISSIM 仿真軟件中車輛是隨機到達的。在軟件中分別建立泊位數從1個到5個的港灣式停靠站和直接式停靠站仿真模型,共計10個模型,仿真時間為1 h,最后得出各個站點所通過最大車輛數,物理泊位數的效率和累計效率值,見表1。從表1可以看出,每增加一個物理泊位所增加的效率是逐漸減少的,4個或者5個停靠泊位的有效泊位比3個停靠泊位也大不了多少。通常在實際泊位數設計時至少需要2個有效停靠泊位,即至少要設置3個物理停靠泊位。
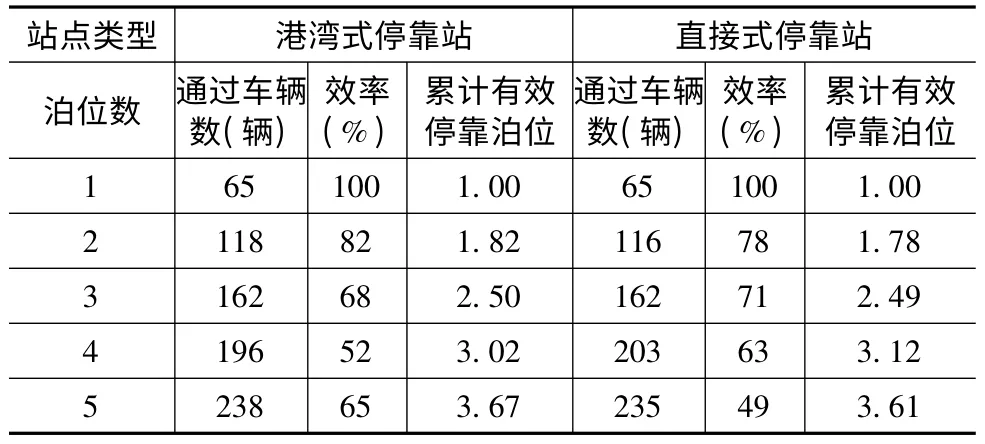
表1 停靠站有效泊位數參考表
2 公交停靠站泊位數設計
2.1 泊位數計算方法一
當公交沿線具有公交專用道,線路發車頻率不高,使得公交車輛行駛干擾較小,車輛到站比較均勻時,根據式(1)計算通行能力,由實際車輛到達率λ,根據下式計算出有效泊位數,參照表1,最后得出實際設計泊位數。這種計算方法可以計算港灣式和直接式停靠站的停靠泊位數。

式中:Nb為停靠站有效泊位數;Bl為單泊位停靠站通行能力;λ為單位時間到站的公交車數。
2.2 泊位數計算方法二
實際車輛到達隨機性較大,近似服從泊松分布,停靠站為車輛停靠服務。所以由排隊論知識,針對停靠站與停靠車流構成一個排隊系統。該排隊系統假設停靠站駛入漸變段只能容納一輛車輛進入,與車流構成單路排隊多通道服務的M/M/N 系統。車輛單列排隊,只要站臺有空閑泊位,車輛按照先到先服務的原則,進站停靠進行上下客服務。這種方法只適用于公交車輛進站時不能超越前車的港灣式停靠站的泊位數。
港灣式停靠站泊位數計算方法如下。根據排隊論可知,系統中沒有車輛的概率為:
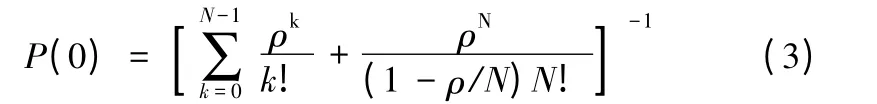
系統中有k 輛車的概率為
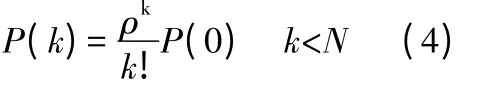
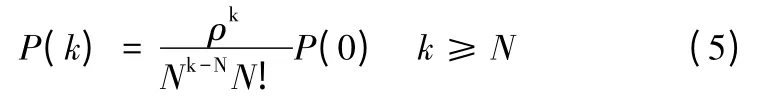
站點平均車輛數為:
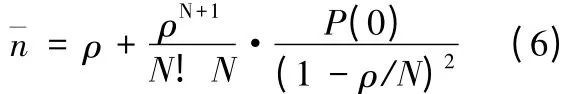
式中:N為系統的通道數,即公交站泊位數;
ρ為服務強度,ρ=λ/μ。對于該系統而言,若ρ/N<1,則系統是穩定的,每個狀態將會循環出現。即到站的公交車將逐步消散;若ρ/N>1,則系統是不穩定的,等候進站的公交排隊將越來越長。因此,確保該系統正常工作的條件是ρ/N<1;
λ為公交車輛到達率,單位時間內到達的公交車輛數(輛/h);
μ為公交停靠站服務率,即單位時間內一個停車泊位服務的公交車數(輛/h);
λ、μ 按照高峰時段取值,設定泊位數初始值N,按照上述公式計算可以得出排隊系統的平均車輛數珔n,判斷:

式中:a為設計失敗率,即公交車在站外等候排隊的概率。通常取0.05~0.10。
3 實例分析
根據重慶市南坪停靠站的公交到達次數和停靠時間調查數據,車輛到達服從泊松分布,高峰小時車輛的到達率λ為160(輛/h),車輛在站平均停靠時間為28 s,標準差為14.25 s,連續兩輛車輛的最小間隔為17 s,臨道交通量為600輛/h.假設車輛不受信號燈控制的影響,請合理設計該站點泊位數(設計失敗率a=0.10)。
3.1 按計算方法一求解
3.1.1 設計成港灣式停靠站
臨道交通量為600 輛/h,則根據圖2,得出tc=14 s;設計失敗率為a=0.10,查表Za=1.28,停靠時間標準差s=14.25 s。則運營裕量tom=sZa=18.24,td=28 s,g/c=1.0。把上述值帶入公式(1)得到停靠站的通行能力為:

3.1.2 設計成直接式停靠站

3.2 按計算方法二求解
由2.2節知道,這種方法只適用于計算車輛不能超越的港灣式停靠站的泊位數。
λ=160(輛/h),μ=3600/(28+17)=80(輛/h),則ρ=λ/μ=2。取N=3,根據式(4),P(0)=0.099,珔n=3.04,由表1,N=3 對應的有效泊位數為Nb=2.50<3.04,不符合條件(7)需要重新計算。
取N=4,根據式(4),P(0)=0.130,珔n=2.17,由于有效泊位數為Nb=3.02>2.17,滿足條件(8)。根據式(5)和式(6),P(1)=0.261,P(2)=0.261,P(3)= 0.174,P(4)= 0.087。P(k>4)=1-P(k≤4)=1-P(0)-P(1)-P(2)-P(3)-P(4)=0.087<0.10,滿足要求。所以按車輛不能互相超越的港灣式停靠站應設計4個泊位。
4 結 論
本文利用VISSIM 仿真軟件分析了清空時間和有效泊位數的取值,并與手冊建議值進行了對比,得到兩者相差較小,反映了仿真軟件在進行交通工程研究的準確性和實用性。然后詳細討論了通行能力分析和排隊論這兩種確定泊位數的方法,前者適用于計算各種停靠站設計形式的泊位數,而后者則只能計算在公交車輛排隊進站,車輛不能互相超越的情況下的港灣式停靠站泊位數,在這種情況下兩種方法計算結果是一致的。綜上所述,本文為停靠站通行能力分析和泊位數設計提供了較為科學而實用的方法。而對于存在非機動車和行人干擾的停靠站通行能力分析和泊位數設計有待于進一步研究。
[1]李娜,陳學武.公交車中途停靠站停靠能力及設計站長計算初探[J].土木工程學報,2003,36(7):72-77
[2]王波.公交專用道上停靠站停車位的計算方法研究[J].交通運輸工程與信息學報,2004,2(4):40-44
[3]Transportation research board.TCRP REPORT 100:Transit Capacity and Quality of Service Manual,2nd Edition[R],2003

