優化復合控制技術在有源電力濾波器中的應用

王雅 魏文新 張維

（1.中國船舶重工集團公司第七一二研究所，武漢430064；2.海軍駐桂林地區軍事代表室，廣西 桂林 541002；3.海

軍駐蕪湖軍事代表室，安徽蕪湖 430033）

0 引言

電力電子裝置和非線性負載的廣泛應用，使得大量的無功電流和諧波電流注入電網，嚴重影響了電網和電氣裝置的安全運行和可靠使用[1]。APF與無源濾波器相比，可以動態的抑制諧波和無功電流，不易與系統發生諧振。近年來，單相APF逐漸成為研究熱點[2]。

目前，對APF的研究主要集中在三相三線和三相四線并聯型APF的指令電流的提取，控制性能的提高上[3,4]，對單相有源電力濾波器的研究顯得不足。對于APF的電流環而言，輸入指令主要為快速變化的諧波信號，PI控制器的帶寬有限，無法做到對這種多個頻率正弦信號疊加的諧波電流的精確跟蹤。基于內模原理的重復控制技術理論上可以實現對正弦指令信號的無靜差跟蹤[5]，但基于工頻周期的調節的重復控制的缺點是動態響應慢，如果設計不當，容易引起相鄰頻率諧波的相互干擾。因此對單相APF，本文提出了一種靜止坐標系下的采用 PI控制和帶前饋的重復控制相結合的電流復合控制策略。重復控制可以有效的增加系統的補償精度，保證輸出電流精確跟蹤給定（負載諧波），前饋環節的引入可以有效的減小相鄰頻率間的相互干擾，有利于提高系統的穩定性，同時有利于增強系統的補償精度，理論上也可以增加重復控制的動態性能。PI控制保證系統的動態性能，理論分析和實驗結果均表明基于 PI和帶前饋的重復控制并聯運行的控制策略穩態精度高，動態響應快，補償性能良好。

1 單相有源電力濾波器模型及其控制系統

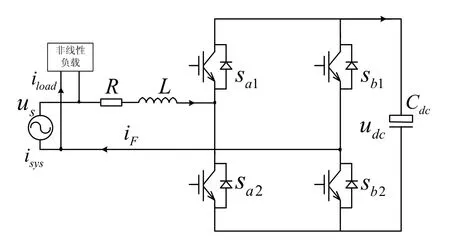
圖1 單相有源電力濾波器電路模型

單相并聯型APF的電路模型如圖1所示，Sa1，Sa2，Sb1，Sb2代表兩個橋臂的開關管，L為 APF的輸出電感，R代表輸出電感內阻和每個橋臂的上下管互鎖死區壓降等效阻抗之和。Cdc代表直流母線上的濾波電容。

由圖1可以建立靜止坐標系下單相APF的數學模型如式(1)所示。

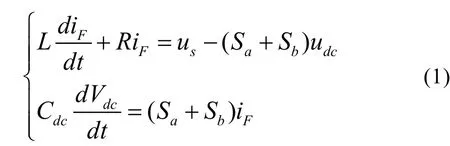
由式(1)可得單相 APF在靜止坐標系下的數學模型框圖如圖2虛線框內所示，圖2中電網電壓是一個擾動量，考慮電網電壓可能存在畸變以及給控制器提供一個穩態運行的工作點，加入電網電壓前饋。

此時引入一個新的控制變量ur

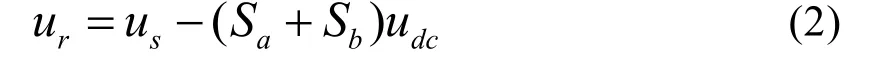
將式(2)帶入式(1)可得：

此時控制對象實際簡化成一個一階慣性環節，Sa1實際相當于APF橋臂中點的輸出電壓。

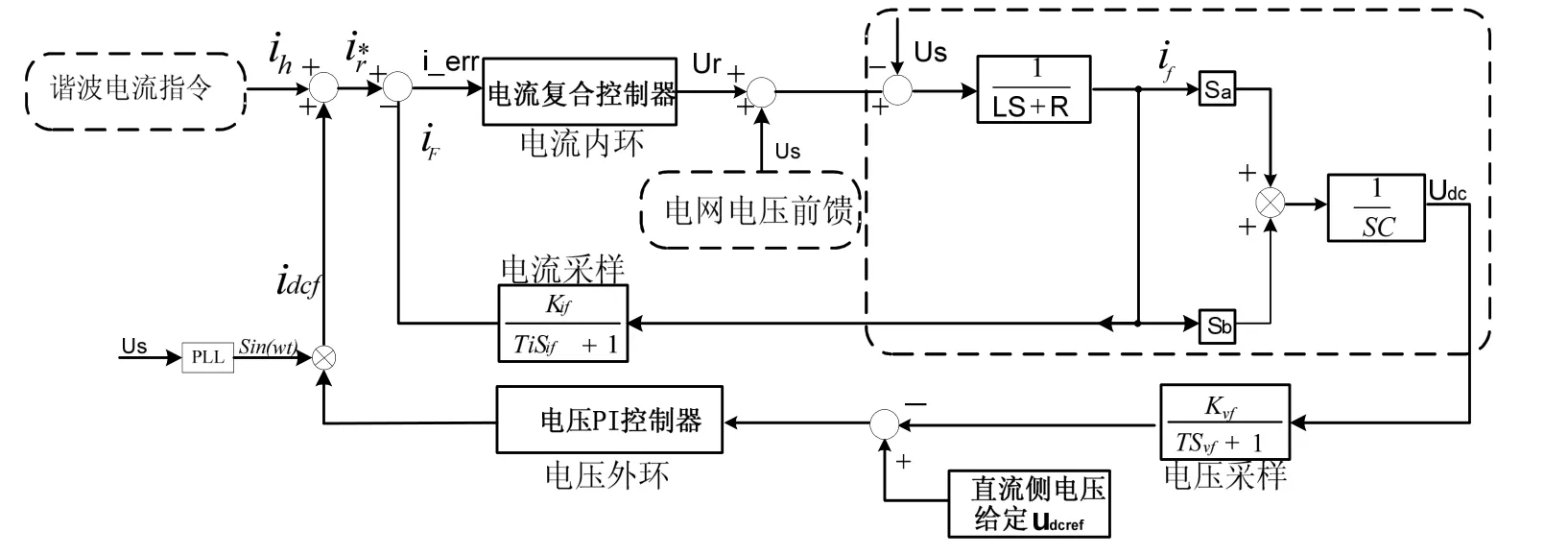
圖2 單相APF控制框圖

2 單相有源電力濾波器控制器參數設計

2.1 重復控制器的分析和設計

重復控制的等效結構圖如圖3所示，N為每周期采樣次數。

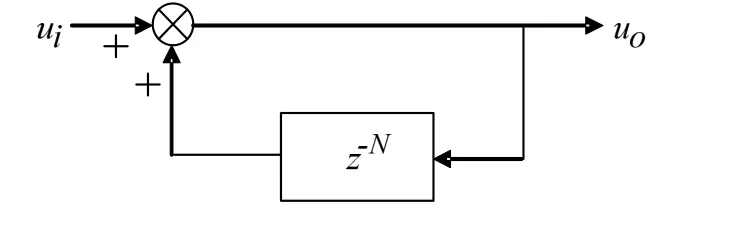
圖3 嵌入式重復控制技術

重復信號發生器的離散形式是：

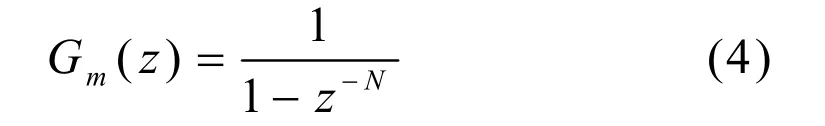
式(4)中N=T/Ts，T為基波周期，Ts為采樣周期。由式(4)可以看出，這是一種類似“純積分”環節的數學形式，這種“純積分”的缺點在于引入了N個位于單位圓圓周上的開環極點，從而使開環系統呈現臨界穩定狀態，只要對象的建模略有偏差，或者對象參數稍微發生變化，閉環系統就極有可能失去穩定，對穩定性和魯棒性不利。因此為了提高系統的穩定性，實際系統大多采用嵌入式的重復信號發生器，增加了濾波器 Q(z)，Q(z)可以是一個低通濾波器，以減弱積分效果，如圖4所示。

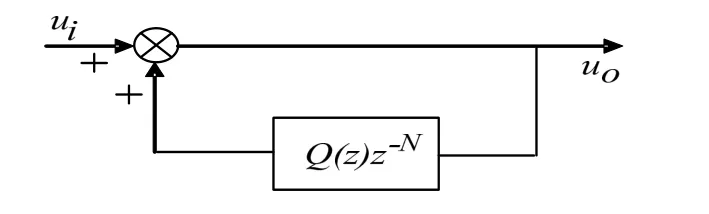
圖4 改進的重復控制技術

其離散化的數學模型為：

一般取Q(z)為一個小于1的常數K，則由式(5)可知，嵌入式重復控制的諧振峰值為1/(1-K)，在節點處的最小增益為1/(1+K)。在改進型重復控制器的基礎上增加一個前饋環節，如圖5所示，引入位于極點之間的零點，諧振峰值由原來的1/(1-K)變為(1+K)/(1-K)，同時在節點處最小的增益由原來的1/(1+K)變為(1-K)/(1+K)，可以獲得更大的帶寬，有利于增強系統的補償精度，提高系統的穩定性。同時鄰極點之間的最小增益減小，使得在同一時間內不同頻率的諧波增強了選擇性。

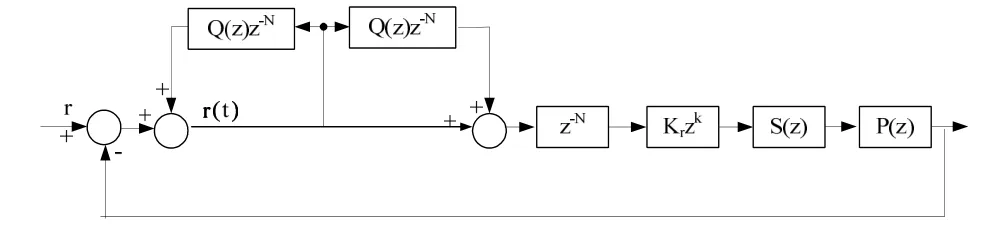
圖5 帶前饋的重復控制器

其輸入輸出關系為：

帶前饋的嵌入式重復控制器結構如圖 5所示，Q(z)是一個低通濾波器，本文中簡單的取為一個小于 1的常數，與周期延遲環節 z-N串聯構成重復控制器的內模部分。S(z)是針對控制對象P(z)而設置的補償器。本文以工頻周期正弦信號作為重復控制的內模進行設計，因此根據內模原理，只要以基波周期重復出現的信號，重復控制器理論上均可以做到對此穩態無靜差的跟蹤。

圖5中，Q(z)不僅與控制系統的穩定性有關，而且與補償精度有關，Q(z)的取值是以犧牲穩態精度來提高系統的穩定性的。本文中取Q(z)=0.95。上文中提到的，控制對象一階慣性環節特性、系統采樣、指令計算和滯后一拍的控制均會增大系統響應的延遲時間。因此用超前拍數環節來補償數字控制的一拍延遲以及控制對象的相位滯后，本文通過估算和實驗驗證選取超前拍數為2，即超前環節為z2，選取合適的Kr來調節重復控制器的收斂速度，Kr不能取的太大，否則容易導致系統的不穩定。本文取Kr＝0.5，此時補償器S(z)設計為KrS(z)。

2.2 PI控制器的分析和設計

由上述分析可知，控制對象可以簡化成一個一階慣性環節，因此基于PI控制的電流閉環控制系統為一個典型的二階系統，可以采用零極點對消的方式將此時的閉環傳函簡化成一階模型，這種方法的核心思想就是使控制器的零點偏移到該系統在S平面的極點。

取比例常數Kp和積分常數Ki為

此時可以得到基于 PI控制的電流環閉環傳遞函數如式(5)所示。

式(8)中Tf為系統響應的延遲時間。由式(8)可知，系統延遲響應時間與比例常數Kp成反比，與輸出電感L成正比，因此減小輸出電感和增大比例常數有助于提高系統的補償精度，但是控制對象一階慣性特性決定了PI控制無法消除延遲，系統采樣、指令計算和數字控制一拍滯后的特性使得電流響應的時間延遲變嚴重，因此增大比例常數、減小輸出電感對輸出電流的跟蹤精度改進有限，而且可能引起其他問題，如導致系統不穩定，引起系統振蕩等。

2.3 改進的復合控制策略分析

為了同時兼顧系統的動態特性和穩態性能，在單相有源電力濾波器控制系統中，將重復控制器與 PI調節器并聯運行使用組成電流復合控制策略，如圖6所示。

當系統穩態運行時，系統的跟蹤誤差小，重復控制占主導作用，PI控制器作用很小；當系統出現大的擾動時，重復控制器由于存在一個工頻周期的延時，在擾動瞬間，一個工頻周期內無法產生調節作用，而PI控制迅速調節，一個基波后重復控制器調節作用使跟蹤誤差減小，直至系統達到新的穩定運行狀態。

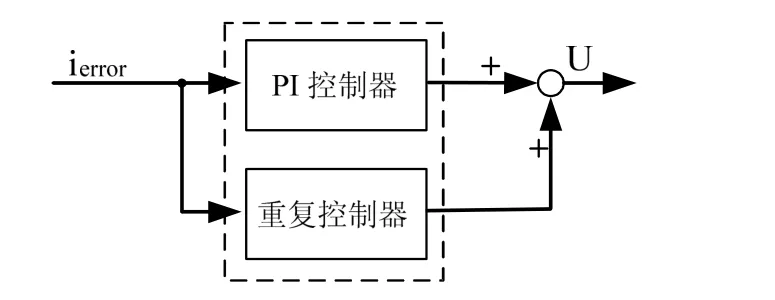
圖6 電流環復合控制器框圖

3 實驗結果

為了理論分析的正確性，在研制的22kVA單相并聯型APF實驗平臺上進行驗證，電路結構參數如表1所示。

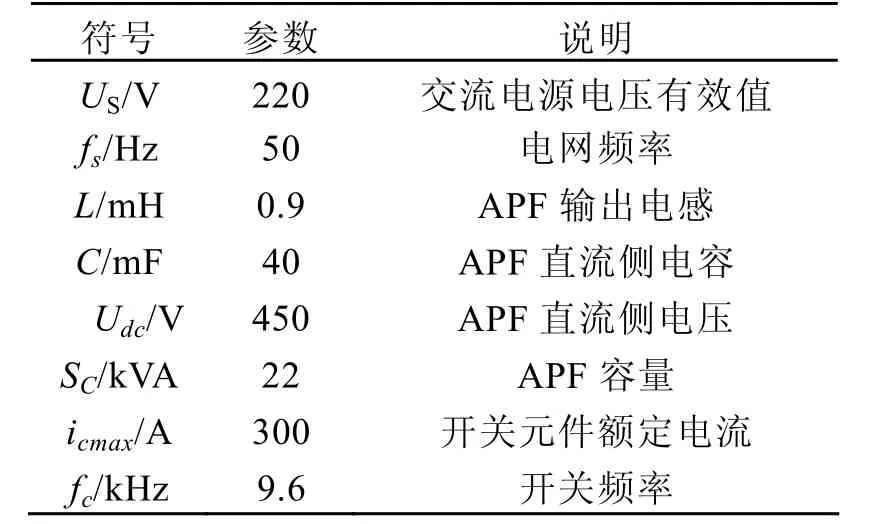
表1 并聯型APF實驗系統電路結構參數

搭建的單相不控整流橋帶 RL型負載作為諧波源，直流側電感和電阻分別為8 mH和5.5 Ω。圖7為非線性負載電流波形，即APF未投入工作時，系統側電流波形，由頻譜分析可以看出，畸變電流為奇數次諧波電流，其中3次諧波畸變率為14.8%，總諧波電流畸變率(THD)為20.4%。

圖7 補償前系統電流波形和頻譜分析

電流內環單獨采用 PI控制時的補償效果如圖8所示，可以看出，在固定點處的電流階躍依舊很明顯，3次諧波畸變率從補償前的 14.8%降低到8.9%，THD由補償前的20.4%降低到13.8%，可見PI的補償效果有限，尚未達到諧波抑制的國家標準。

采用 PI控制和帶前饋的重復控制并聯運行的電流復合控制策略下，補償效果如圖9所示。3次諧波畸變率從14.8%降低到1.73%，THD下降至 3.6%，補償精度得到顯著提高，波形質量得到明顯改善，達到了諧波抑制的國家標準。

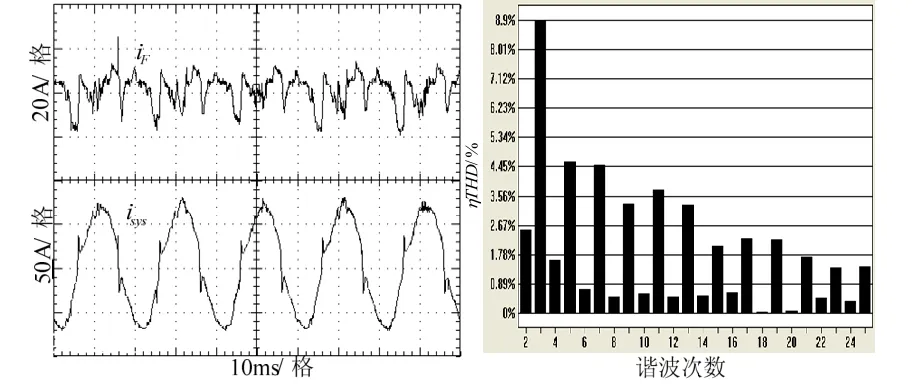
圖8 單獨PI控制器時系統電流和電流頻譜

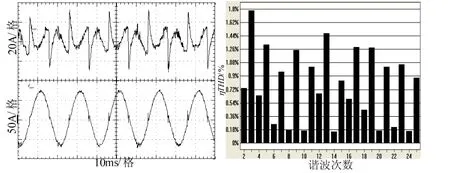
圖7 復合控制補償時系統電流和電流頻譜

4 結論

本文分析了PI控制器在單相APF中應用的局限性，為改善單相APF穩態時補償精度，同時兼顧其動態響應特性，提出了PI控制器和帶前饋的重復控制器相結合的電流復合控制策略，并從理論上分析了帶前饋的重復控制的優勢。實驗結果表明改進的復合控制策略可以明顯提高單相APF的補償性能，達到了諧波抑制的國家標準。

[1]王兆安, 楊君, 劉進軍.諧波抑制和無功功率補償[M]. 北京： 機械工業出版社, 1998

[2]T. Tanaka, E.Hiraki, K.Ueda, K.Sato, S.Fukuma. A Novel Detection method of active and reactive currents in single phase circuits using the correlation and cross-correlation coefficients and its applications[J]. IEEE transactions on power delivery, 2007, 4(22)：2450-2456.

[3]李戰鷹, 任震, 楊澤明. 有源濾波裝置及其應用綜述[J]. 電網技術, 2004, 28(12)： 40-43.

[4]李江, 孫海順, 程時杰等. 基于灰色系統理論的有源濾波器預測控制[J]. 中國電機工程學報, 2002,22(2)： 6-10.

[5]Robert Gri?ó, Rafael Cardoner, Ramon Costa-Castelló,Enric Fossas. Digital repetitive control of a three-phase four-wire shunt active filter[J]. IEEE transactions on industrial electronics, 2007, 54(3)：1495-1503.