雙目標純方位定位數據處理分析

唐揚 劉承禹 胡科強

（1. 海軍工程大學兵器工程系，武漢430033；2. 二炮研究院，北京100085）

0 引言

單個矢量水聽器無法直接測得水下目標的距離增加了量測的不確定性[1～4]，失去觀測站本身所具有的定位跟蹤能力。不借助其他傳感器，觀測站只能轉換到被動。被動工作方式所獲得的定位跟蹤目標的定位精度，要低于沒有干擾的情況。測角誤差對定位跟蹤精度的影響一般要大于測距誤差，所以研究有效的被動傳感器定位跟蹤數據關聯算法具有較高的理論價值和現實意義。

本文利用時空關聯迭代找到目標同一時刻散射的水聲信號在兩方位序列中的位置，采用航真狀態轉移和平滑窗相結合以減小數據波動和實現航真管理實現雙目標的有效跟蹤，并對跟蹤性能進行了仿真實驗。

1 純方位定位解算原理

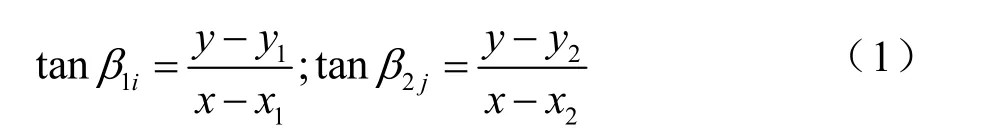
P的坐標為：

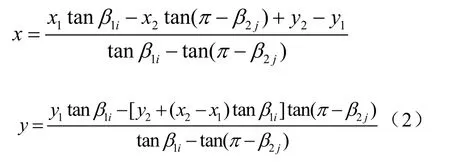
考察兩個浮標的關聯問題，浮標i保留原方位序列，即根據真真真值點的直角坐標，直接換算成該浮標的方位數據。取k時刻及k+1時刻的真真真值點，作線性插值，可產生浮標 j的方位序列，需確定相對延遲點數Δk及時延修正量δi：

式中： R ound[·]表示四舍五入，c為聲速，T為數據采樣率。于是， β2(k +Δk )與β1(k)建立了基本的時空關聯。其次，對該式[·]內的量值取小數部分，賦予δi，再基于k時刻真真真值點坐標，以v? T?δi（v為目標航速）步長向k+1時刻真值點方向插值，換算成方位數據，添入 β2(k + Δk )即可。若 δi＞0.5，則上述過程中的δi以1-δi代之，且基于 k +1時刻真真點向k時刻真真點反向插值。至此，生成了用于仿真的方位數據序列。此時，若利用同時刻的β1(k)與β2(k)進行跟蹤，將產生偏量，稱做無關聯解算。實際解算，需利用文獻[6]的迭代算法進行關聯。

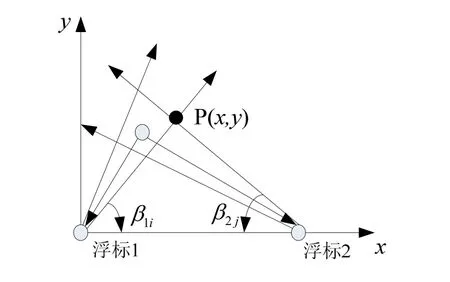
圖1 雙基陣純方位定位解算原理圖

2 卡爾曼濾波器用于純方位TMA

卡爾曼濾波的基本出發點是建立恰當的數學模型，即描述動態過程的狀態方程和量測方程。

取狀態矢量為：

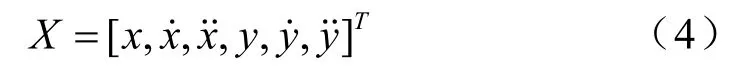
觀測矢量為：

則相應的狀態方程和測量方程分別為：

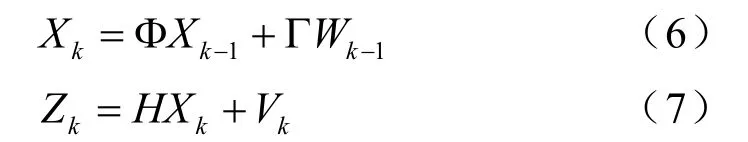
其中，Φ是狀態轉移矩陣，Γ是隨機擾動加速度狀態轉移矩陣，H是測量矩陣，它們分別滿足：

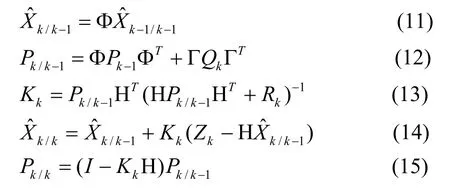
采用三點法得到初值，用限定下限法抑制濾波器發散[7]。

3 航真狀態轉移處理

利用門限鑒別法判別“野值”，即每個測量點真都與濾波器的預測點真進行比較，若其間距超過預設門限 D(取值與上節所述相同)，則暫定為“野值”，作為試探航真 A[8]的初值加以保留，而濾波器仍以預測值代替測量值繼續進行處理，在處理中使用三階非線性擬合套以 26點滑動時間窗，然后進行卡爾曼濾波處理。如圖2。

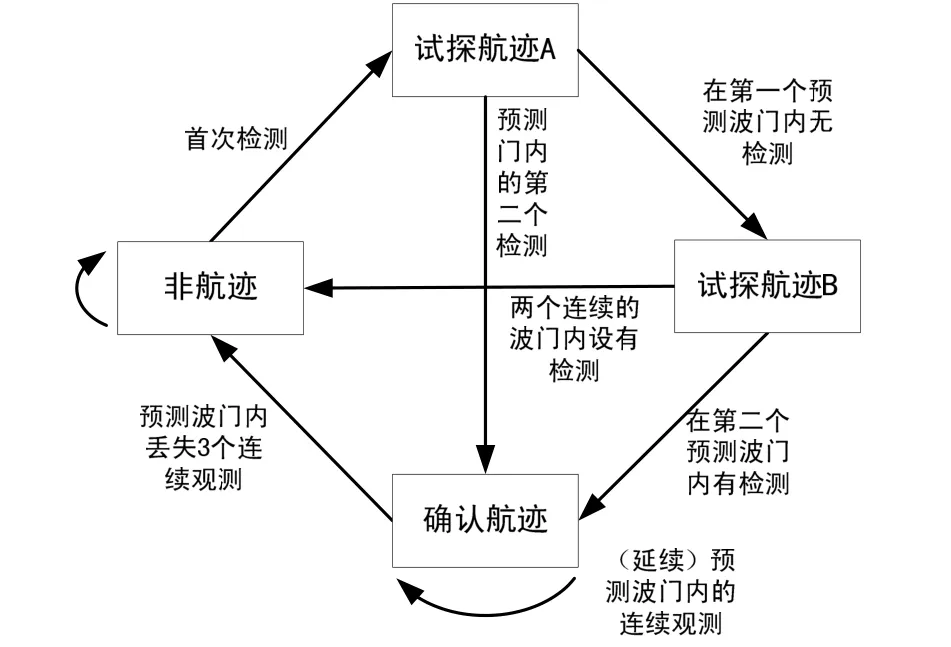
圖2 航真狀態轉移圖

基于航真狀態轉移的目標跟蹤處理軟件流程如圖3所示。

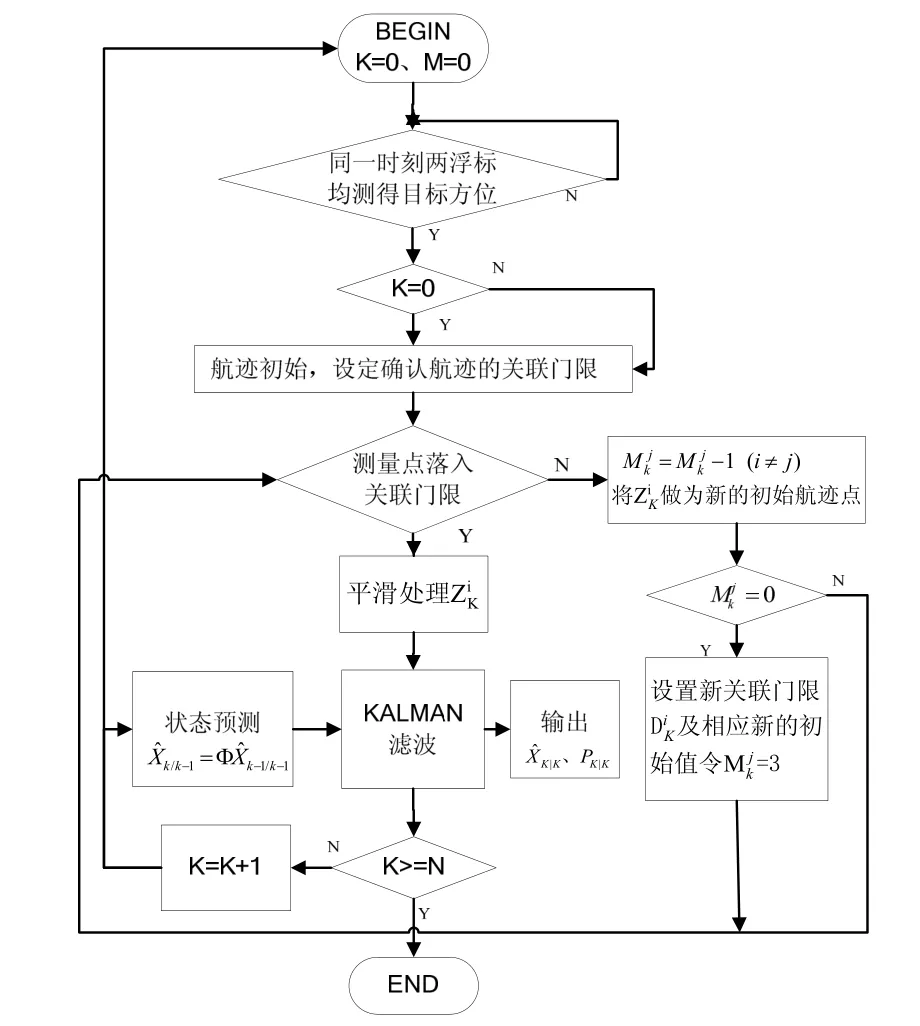
圖3 程序流程圖

4 仿真實驗與分析

我們對上面分析的雙基陣純方位 TMA方法進行了仿真計算。圖4給出的是數據關聯前后，卡爾曼濾波仿真的結果，圖5、6給出了兩種情況下的距離誤差比較。從圖可以看出，雙基陣純方位 TMA的目標估計是收斂的，且數據無關聯解算表現為有偏測量，其解算結果與真實情況相比產生了很大的偏量，而數據關聯后則基本消除了兩浮標的時空差異所帶來的影響。

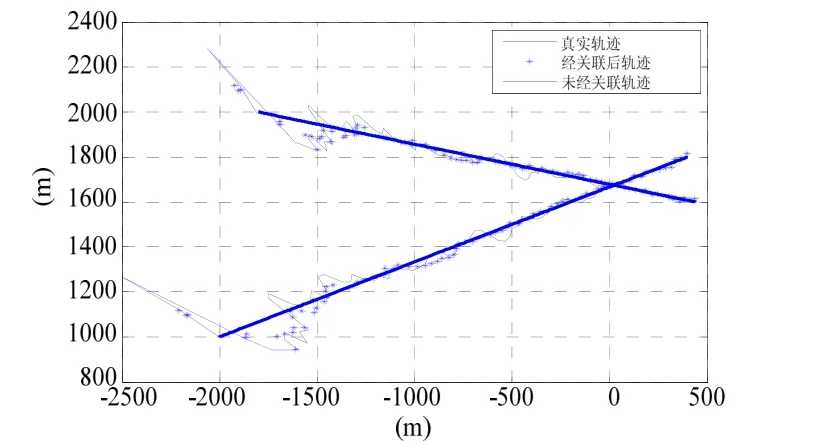
圖4 真真跟蹤

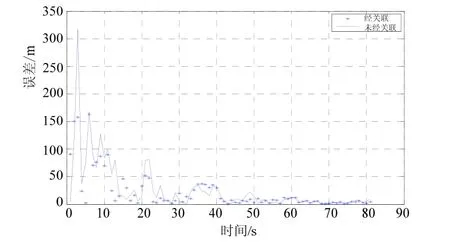
圖5 目標1誤差比較圖

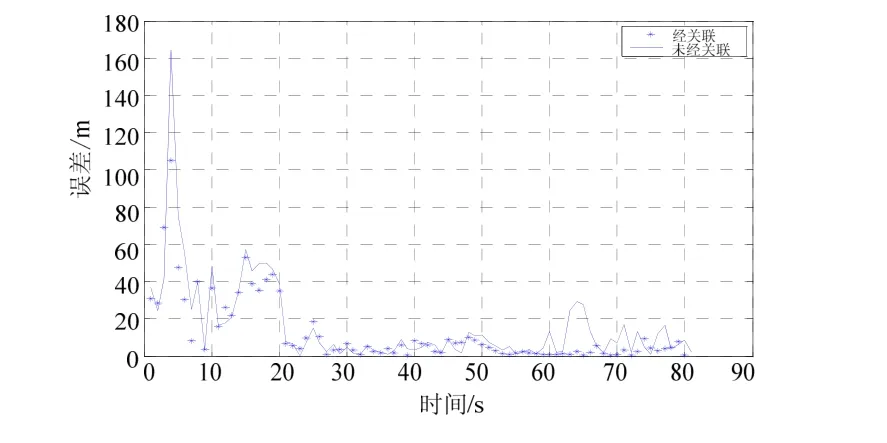
圖6 目標2誤差比較圖

5 結論

本文對雙基陣純方位定位中數據時空校準，航真狀態轉移和航真管理進行了研究，分析了數據關聯、航真狀態轉移、平滑濾波對卡爾曼濾波和實時目標跟蹤的影響效果。通過仿真實驗，數據關聯有效消除了兩浮標的時空差異所帶來的影響，提高了算法的穩定性和全局收斂性；通過航真狀態轉移進行航真管理實現雙目標的實時跟蹤處理。

[1]MR. Garey and D.S .Johnson, Computer sand Intract ability： A Guide to the Theory of N-P Completeness.SanFrancisco, CA： Freeman,1979.

[2]C.H.Papa dimitriouand K. Steiglitz, Combinatorial Optimization： Algorithms and Complexity E nglewood Cliffs, N J：P rentice-Hall,1982 .

[3]Ljung L. Asymptotic behavior of extended kalman filter as a parrameter estimator for linear system[J].IEEETransonAutomatticControl,1979,24(1)：36 -50.

[4]YANG Yuan-xi，GAO Wei-guang.A new learning statistic for adaptive filter based on predicted residuals [J].Progress in Natural Science, 2006, 16(8)：833-837.

[5]孫仲康, 周一宇, 何黎星. 單多基地有源無源定位技術[M]. 北京： 國防工業出版社, 1996： 234-241.

[6]樊羚珂. 卡爾曼濾波在被動測距聲納中的應用[J].哈爾濱船舶工程學院學報, 1986, 59-66.

[7]王燕. 水下目標被動定位仿真研究[D]. 哈爾濱工程大學, 2000, 31-33.

[8]劉同明. 數據融合技術及其應用[M]. 北京： 國防工業出版社, 2000, 168-175.