關于一個二元整數函數正負性的研究

李 強

（大慶職業學院工商管理系 黑龍江 大慶 163000）

0 引言

我們要研究的二元整數函數為：

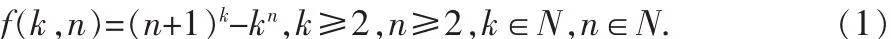
此問題源于我們要論證的一個數論問題，本文的目的就是考查該函數在其定義域內函數值符號的變化情況.

1 引理及定理

此結果可借助函數的導數知識簡單推得，故略.

引理2當n≥7時，有：

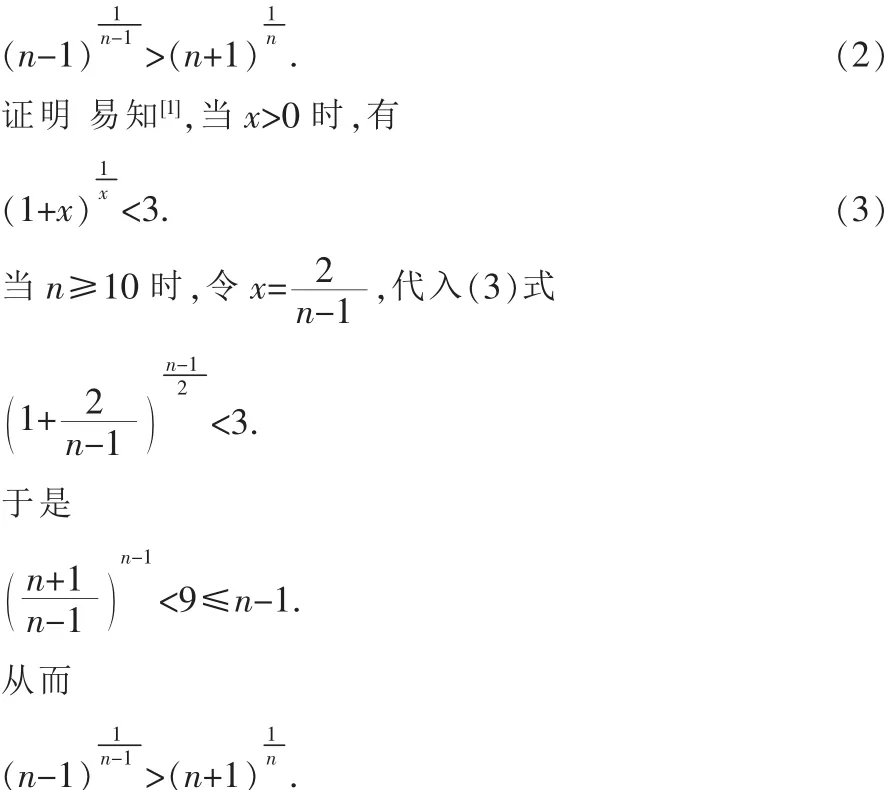
容易驗證當n=7，8，9時，上式也成立.命題得證.

定理 1 當 k≥n≥2 時，有：f（k，n）＞0.

證明 當n＝2時，根據引理1有

由（4），（5），（1）式知，定理成立.

定理 2 當 n≥7，2≤k≤n-1 時，有：f（k，n）＜0.

證明 當 n≥7 時，有：n－1≥6.

由（1）式知，定理成立.

根據定理 1 知，陣列（f（k，n））（k≥2，n≥2）的對角及下三角塊上的元素都為正數。而由定理2，當列數n≥7時，上三角塊中的元素均取負數.再經過驗知：f（2，3），f（2，4），f（2，5），f（3，4），f（4，5），f（5，6），取正，而 f（2，6），f（3，5），f（3，6），f（4，6）取負.綜上，我們可得下表.

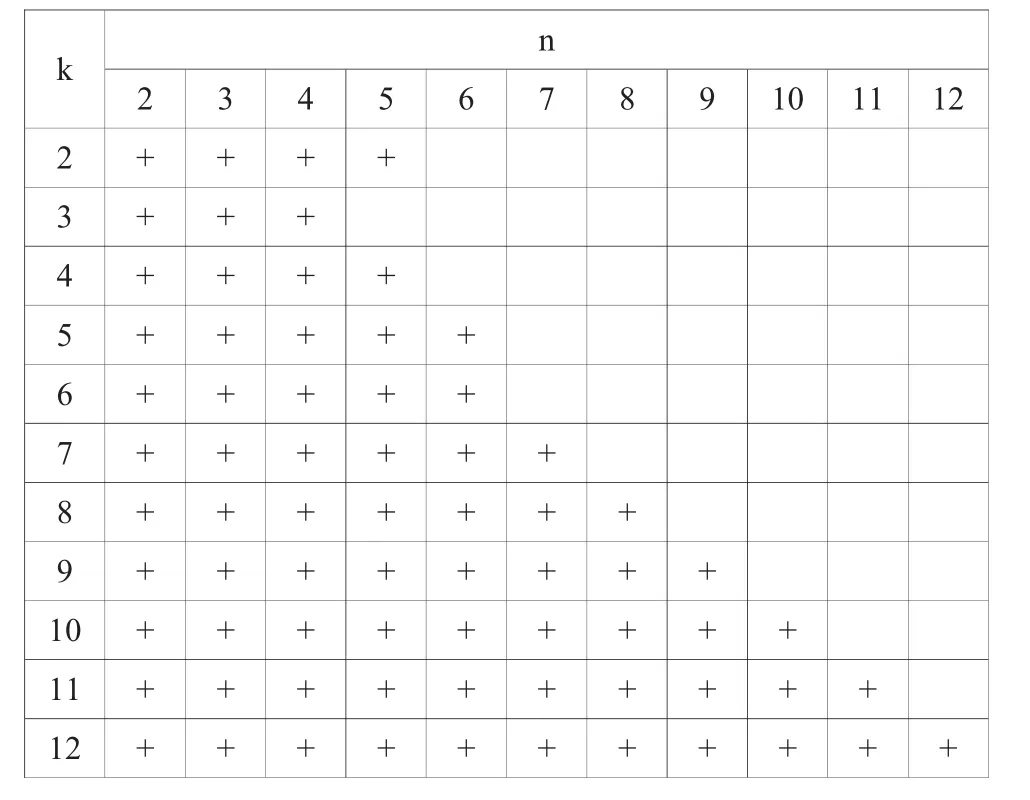
表1 二元整數函數f（k，n）的符號變化（空白代表函數在該處的取值為負）

具體地，我們通過MATLAB編程計算出了當2≤k，n≤9時，二元整數函數 f（k，n）的取值情況.

由表2可見，表1所得到的結果是完全正確的.

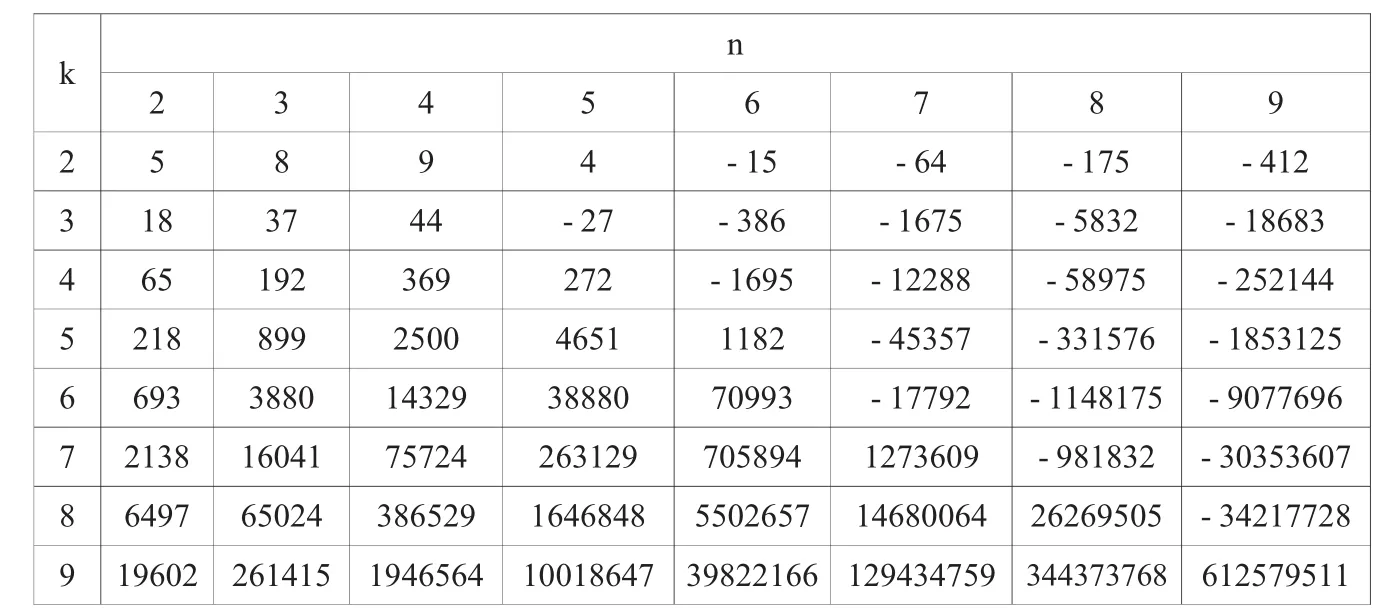
表2 二元整數函數f（k，n）的部分函數值

2 小結

本文通過函數的單調性等相關知識，探求了二元整數函數f（k，n）函數值符號的變化規律，得到如下結論：

函數 f（k，n）在其定義域｛（k，n）｜k≥2，n≥2，k∈N，n∈N｝內各點處的取值均不為零.其中，位于陣列（f（k，n））對角及下三角塊上的元素均取正號，位于上三角塊中的元素當列數n≥7時取負號，而當列數2≤n≤6時，需要計算才能確定其符號.

上述結果不僅利于我們對二元整數函數 f（k，n）性質的理解，還能從中生成系列不等式.例如：當n≥7，2≤k≤n-1時，有：

而不等式（8）可用于解決數論等一些相關的問題.此外，關于函數 f（k，n）的符號判定問題，也可通過數學歸納法、均值不等式等其他數學工具加以解決.

［1］常庚哲，史濟懷.數學分析教程[M].北京：高等教育出版社，2003.

［2］Helmut Hasse.Number Theory[M].北京：世界圖書出版公司，2010.

［3］鄭毓信.數學方法論[M].南寧：廣西教育出版社，2003.

［4］G.波利亞.數學與猜想[M].北京：科學出版社有限責任公司，2011.