未來理財 FOF說了算!
葉輝
基金總數(shù)比股票還多了,怎么買?
讓專業(yè)的人幫你選基金,
買“基金中的基金”FOF,
收益更好,風(fēng)險更小。
理財會經(jīng)歷三個階段:
散戶時代,基金時代,F(xiàn)OF資產(chǎn)配置時代。
未來理財,F(xiàn)OF說了算!

上海普陀區(qū)的張梅在一家事業(yè)單位上班,在朋友眼里她是個理財達(dá)人。張梅是中國最早一代股民,但折騰多年不賺錢后,她從10多年前轉(zhuǎn)而買基金,炒黃金,也投資過信托,斬獲頗豐。最讓張梅滿意的還是基金投資,因為她買了好幾只不錯的基金,在華夏大盤精選一只基金上甚至賺了將近10倍。華夏大盤精選由前公募一哥王亞偉管理,在2007年之后封閉了好幾年,張梅提前一年就買了這只基金。
不過,以“老司機”自居的張梅如今也開始苦惱,以前隨便買一只基金都很容易賺錢,“現(xiàn)在基金太多,都不知道怎么挑了”。像張梅一樣存在困惑的“理財老司機”還有不少:現(xiàn)在基金總數(shù)已經(jīng)有3300多只,超過了A股上市公司數(shù)量。挑選優(yōu)質(zhì)的基金,已經(jīng)越來越需要專業(yè)技術(shù)了。
未來理財,F(xiàn)OF說了算! FOF理論上的好處是,讓專業(yè)的人幫你選基金,買“基金中的基金”,收益更好,風(fēng)險更小。最近財經(jīng)媒體鋪天蓋地都是FOF相關(guān)的報道,為什么?因為FOF是未來的趨勢,能解決張梅等投資者挑選基金的苦惱。
備受矚目的FOF
什么是FOF?它最近為什么備受矚目?雖然FOF在全球資產(chǎn)配置中占有重要的一席之地,但對于中國證券投資市場來說,專業(yè)投資者都很熟悉,對普通人來說還稍顯陌生。
FOF(Fund of funds,基金中的基金),是指投資于基金組合的基金,首先出現(xiàn)于上世紀(jì)70年代的美國,尤其是近10年來,它已成為海外個人投資者的主流投資方式。由于FOF在選擇投資標(biāo)的時有較大的靈活性,因此,越是在低迷或波動的市場環(huán)境下,越能襯托出FOF的優(yōu)勢。
“FOF是基金行業(yè)發(fā)展到一定程度后的必然產(chǎn)物。據(jù)中國基金業(yè)協(xié)會的數(shù)據(jù),截至8月份,我國公募基金產(chǎn)品數(shù)量達(dá)到3296只,這比滬深兩市上市公司總數(shù)還要多。面對如此多的基金產(chǎn)品,投資者很難有精力和專業(yè)知識尋找、跟蹤和管理自己的基金投資。而FOF則是借助基金管理人的專業(yè)能力,選擇基金,有利于投資者進行多元化配置,自然發(fā)展?jié)摿薮蟆V袊陂_啟‘基金中基金投資的全新時代。”全球最大的FOF/MOM管理機構(gòu)羅素投資董事長兼首席執(zhí)行官Len Brennan如是表示。
羅素投資成立于1936年,公司全球咨詢業(yè)務(wù)量達(dá)2.3萬億美元,管理資產(chǎn)2400億美元,作為全球最大的FOF/MOM管理人,在資產(chǎn)管理行業(yè)中擁有權(quán)威性地位。
業(yè)內(nèi)人士指出,投資機會隨時可能出現(xiàn)在任何市場、任何范疇,沒有哪一類產(chǎn)品可以永遠(yuǎn)獨占鰲頭。FOF多元資產(chǎn)投資策略可以根據(jù)不同的市況,側(cè)重于不同類別的投資產(chǎn)品,從而及時捕捉機會,分散風(fēng)險。
歌斐資產(chǎn)負(fù)責(zé)人郭弘仁是一位臺灣人,也曾經(jīng)在羅素就職,因為看好內(nèi)地火熱的發(fā)展前景,他從美國跳槽跑來做FOF。郭弘仁認(rèn)為,理財會經(jīng)歷三個階段,散戶時代,基金時代,F(xiàn)OF資產(chǎn)配置時代。股票太多了,自己沒法挑選股票時,幫你挑股票的基金應(yīng)運而生;當(dāng)基金太多了,自己沒法挑選基金時,幫你挑選基金的FOF應(yīng)運而生。他認(rèn)為,未來FOF將幫助大部分家庭解決資產(chǎn)配置問題。
廣發(fā)基金資產(chǎn)配置部投資經(jīng)理朱坤表示,中國投資者面臨無風(fēng)險高收益時代的終結(jié),在資產(chǎn)荒的背景下推出FOF這種資產(chǎn)配置類型業(yè)務(wù),具有它的歷史必然性。基金本身就有平滑市場波動的優(yōu)勢,而FOF則將這種優(yōu)勢進一步放大。對于追求長期穩(wěn)定收益的客戶,波動較小的FOF對于投資者來說優(yōu)勢更加明顯。
沸騰的基金圈
“忽如一夜春風(fēng)來,千樹萬樹梨花開。”

隨著監(jiān)管層發(fā)布公募FOF產(chǎn)品相關(guān)指引,支持基金行業(yè)推出基金中的基金,公募基金公司也紛紛招兵買馬,積極備戰(zhàn)。易方達(dá)等基金公司,甚至直接從美國華爾街挖人。
公募FOF產(chǎn)品已進入倒計時階段。在10月份眾多FOF基金經(jīng)理通過考試之后,11月22日首批FOF基金經(jīng)理注冊函全面下發(fā),這也意味著當(dāng)天就能正式上報公募FOF產(chǎn)品。據(jù)了解,基金公司為了搶發(fā)首只,動作最迅速的當(dāng)天就已經(jīng)上報相關(guān)產(chǎn)品。
不過,第一只公募FOF什么時候面世還存在不確定性。因為FOF類產(chǎn)品注冊要走普通通道,按照慣例,審批時間可達(dá)6個月,首批產(chǎn)品未必能在今年年底面市。因此,首批公募FOF產(chǎn)品距離正式上報依舊還有“最后一公里”。
各家基金公司都在備戰(zhàn)FOF,并且密集舉行各種研討會。在11月15日舉行的上投摩根FOF投資研討會上,上投摩根基金國際投資部總監(jiān)張軍認(rèn)為,集中“押寶”單個策略的投資方式弊端逐漸顯現(xiàn),多元化配置戰(zhàn)略在投資回報和風(fēng)險波動兩方面的平衡則顯示出比較突出的優(yōu)勢,F(xiàn)OF產(chǎn)品發(fā)展?jié)摿薮蟆I贤赌Ω趥鋺?zhàn)國內(nèi)FOF的同時,已經(jīng)在11月下旬發(fā)行了一只投資海外的FOF的QDII產(chǎn)品。
根據(jù)記者的初略統(tǒng)計,已經(jīng)有10多家基金公司在“摩拳擦掌”,準(zhǔn)備了相關(guān)產(chǎn)品搶“頭啖湯”,大多都是資產(chǎn)管理規(guī)模比較靠前的基金公司。
據(jù)悉,不少基金公司第一批FOF定位于“絕對收益”類產(chǎn)品,為吸引更多的低風(fēng)險偏好資金,有些公司計劃引入“類保本”的CPPI策略。北京一家中型基金公司相關(guān)人士表示,目前公司已經(jīng)準(zhǔn)備了5只產(chǎn)品,從保守到激進風(fēng)格都有,但是會“擇機上報”,前期會保守一些。
2017年FOF有望井噴
華夏基金公司、羅素投資集團聯(lián)合中國基金報11月19日在北京共同主辦了一個論壇,名字就叫“2016中國FOF元年高峰論壇”,可見基金業(yè)對FOF的期待。
雖然目前公募基金在FOF產(chǎn)品方面尚未取得實質(zhì)性進展,發(fā)行上都還在排隊,但業(yè)內(nèi)人士一致認(rèn)為,2017年FOF產(chǎn)品有望井噴。
以最新公布的公募基金總體規(guī)模超過8萬億元估算,參考美國共同基金中FOF規(guī)模占比超過10%,如果進行簡單推算,業(yè)內(nèi)人士預(yù)期,未來中國公募FOF規(guī)模有望超過1萬億元。這是一個巨大的市場。
為此,華夏基金公司攜手全球領(lǐng)先的FOF/MOM管理人羅素投資集團,希望用華夏基金的本土投研優(yōu)勢,加上羅素投資豐富的海外資產(chǎn)配置經(jīng)驗,強強聯(lián)合為投資人提供更好的產(chǎn)品和服務(wù)。據(jù)記者了解,為了更好地進行FOF基金管理,華夏基金從去年開始重點布局行業(yè)基金,發(fā)行了包括醫(yī)療、消費、制造業(yè)、軍工、科技等多只行業(yè)基金,將行業(yè)的深度研究變?yōu)榭晒〧OF基金投資的子基金產(chǎn)品,同時,對現(xiàn)有產(chǎn)品進行分析,逐步穩(wěn)定基金的投資風(fēng)格,成為可供FOF基金投資的具有穩(wěn)定風(fēng)格的子基金產(chǎn)品,完善而豐富的產(chǎn)品線為FOF基金投資提供了可行性。
不過,就目前來看,F(xiàn)OF發(fā)展依然面臨不少問題。農(nóng)銀匯理基金副總經(jīng)理兼市場總監(jiān)施衛(wèi)直言,投資者教育不足、市場適應(yīng)性較低、投資管理人才缺乏等都是基金公司需要面對的問題和挑戰(zhàn)。
國外FOF增速更快
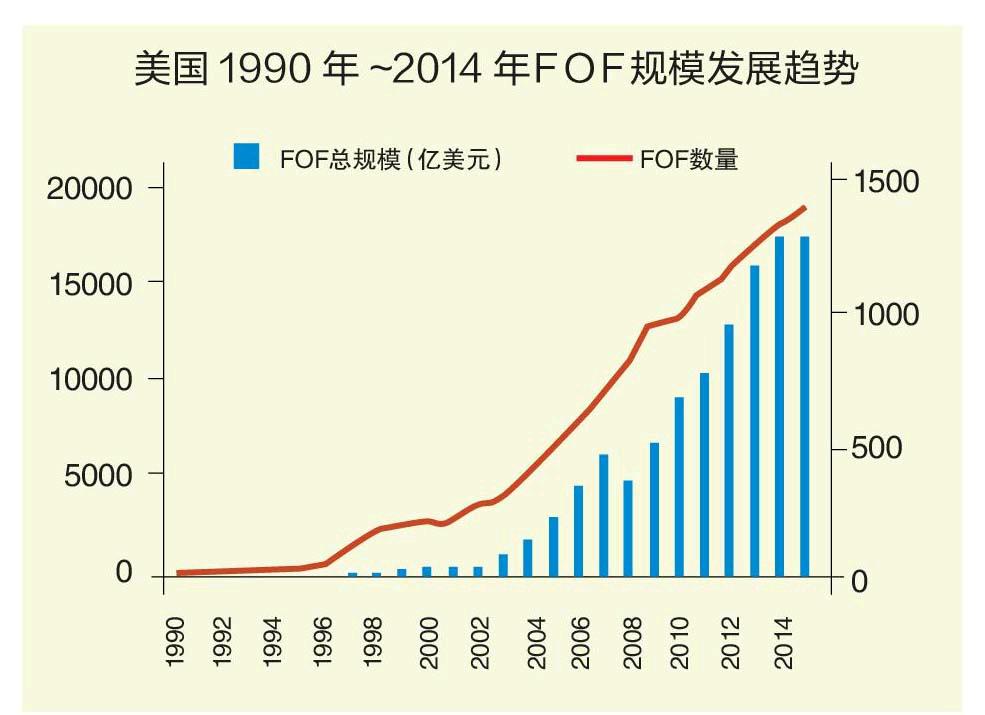
據(jù)公開資料顯示,到2013年年底,美國一共有1267只FOF的產(chǎn)品,而截至2015年年末,美國市場公募FOF規(guī)模達(dá)到1.7萬億美元,占公募基金規(guī)模的比例為11%;同時,F(xiàn)OF近五年規(guī)模增速達(dá)到13.8%,比普通公募基金規(guī)模增速高出2倍左右。
在英國,F(xiàn)OF同樣受到追捧。根據(jù)英國投資協(xié)會最新數(shù)據(jù)顯示,2015年英國的FOF凈銷售額為37億英鎊,較2014年的31億英鎊上升近20%。此外,在資產(chǎn)總規(guī)模上,F(xiàn)OF規(guī)模已經(jīng)占到了英國基金業(yè)管理總資產(chǎn)的12.6%。從總銷售額來看,2015年上半年,F(xiàn)OF基金銷售額占到了行業(yè)總銷售額的52%。
“他山之石,可以攻玉。我國FOF剛剛起步,而在發(fā)達(dá)市場,F(xiàn)OF已經(jīng)發(fā)展了30多年,規(guī)模從十幾億美元增長到上萬億美元。” 華夏基金總經(jīng)理湯曉東稱。
如何配置FOF?
公募FOF即將問世,如何選擇FOF的新問題日漸急迫。
根據(jù)發(fā)達(dá)國家的經(jīng)驗,國內(nèi)的FOF也會分成兩類,一類是純投資本公司基金產(chǎn)品的內(nèi)部FOF,免收了雙重收費,美國發(fā)展得比較好的都是這類產(chǎn)品。另一類是可以投資其他公司基金產(chǎn)品的外部FOF。
有人作了一個形象的比喻,好的FOF就像組建一支艦隊,艦隊中需要各式各樣不同的艦艇,比如驅(qū)逐艦、潛艇等等,各有優(yōu)勢和功能,在艦隊中扮演不同角色,確保艦隊可以應(yīng)對不同的風(fēng)險,具有很強的戰(zhàn)斗力。
對于如何配置FOF,廣發(fā)基金資產(chǎn)配置部投資經(jīng)理陸靖昶認(rèn)為是“99%的科學(xué)+1%的藝術(shù)”。所謂“科學(xué)”,是指基于成熟理論的資產(chǎn)配置框架;所謂“藝術(shù)”,則是來自于自身資產(chǎn)配置小組的個性建議。廣發(fā)基金對于FOF的解決方案目前包括配置型FOF、相對收益FOF和特殊目標(biāo)FOF,多種資產(chǎn)配置模型對應(yīng)不同客戶需求。
據(jù)悉,其他基金公司的FOF產(chǎn)品定位與之類似,各家公司產(chǎn)品類別差異不大,但以后的管理水平可能會有比較大的差別。
針對市場的一片叫好之聲,長信基金FOF投資部總監(jiān)鄧虎也提醒說,F(xiàn)OF并不是“萬能藥”。在其看來,F(xiàn)OF只是FOF,是一種投資結(jié)構(gòu)和形式,具體的風(fēng)險收益情況、策略乃至最終表現(xiàn)都可能千差萬別,這與FOF自身的目標(biāo)以及FOF投向的基金相關(guān)。公募FOF的意義在于真正實現(xiàn)了將FOF納入普通投資者的選擇范圍,市場也將真正迎來體現(xiàn)基金投資能力的產(chǎn)品。
北京一位不愿意透露姓名的基金經(jīng)理告訴記者,目前國內(nèi)已經(jīng)有不少類FOF產(chǎn)品,都是銷售機構(gòu)把握住投資者選基金難的需求而推出的,簡單綁定幾只所謂知名的基金,沒有對投資策略的深刻思考,沒有資產(chǎn)配置的主動管理,都是偽FOF產(chǎn)品。在投資FOF時,也要對基金經(jīng)理的投資風(fēng)格和理念有所了解,才能知道這項投資是否能真的可以規(guī)避風(fēng)險。

