基于瞄準多個目標航天器的空間攔截器停泊軌道優化

2012-07-09 02:33:04向明思

兵器裝備工程學報 2012年12期

關鍵詞：優化

楊亮，武健，向明思

(第二炮兵工程大學906 室，西安 710025)

空間是未來的戰略高地，誰控制了太空，誰就占據了主動。空間攔截與反攔截的不斷發展將使空間爭奪戰更加激烈。空間停泊武器能有效攔截敵方外層航天器，它是各國爭相發展的對象。

當前國內學者對空間停泊武器的研究主要集中于對單個目標航天器的機動攔截上。美國著名的“智能卵石”計劃主要使攔截器小型化、輕型化且制導性能更優并使其在空間大量部署。本文有別于此，探討單個攔截器預備攔截一組多個目標的停泊軌道優化研究。

考慮為未來空間爭奪戰節約資源、提高效率的設想，現假定某一在停泊軌道上正常運轉的空間攔截器預備瞄準一組多個目標，當命令下達后攻擊一個特定目標。由于目前近地軌道上各種非合作航天器數目眾多，且有部分軌道部署比較集中，所以本文設想可以實現。于此，本文應用固定時間最小能量機動攔截模型并設定停泊軌道參數變化值域及解算步長，通過改進遺傳算法對每次步長進行仿真計算，得到最小的速度增量累加值，最后找到一條滿足任務約束的能量最優的攔截器停泊軌道。

1 固定時間最小能量攔截模型

在此只考慮橢圓軌道情況且假定地球為均質圓球，攔截器通過脈沖作用獲得瞬時速度增量及在攔截過程中不考慮攝動因素影響。

攔截過程如如圖1 所示，攔截器運行初始軌道為軌道Ι，t 時刻攔截器的位置矢量和速度矢量分別為r1和v1，假定在該時刻對其施加速度沖量Δv，使攔截器的速度矢量變為ν2，并進入另一條軌道F，經Δt 秒后命中預定的空間位置矢量為vm的目標衛星。

圖1 軌道攔截示意圖

記軌道F 的半通徑為P2，偏心率為e2，則r1和r2的夾角為Δf(即真近點角之差):

設定

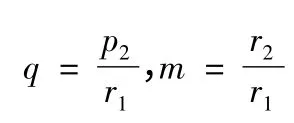
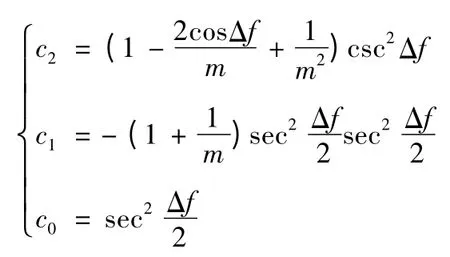
根據活力公式及動量守恒定理即可計算v2(Θ2為終極軌道的速度傾角)

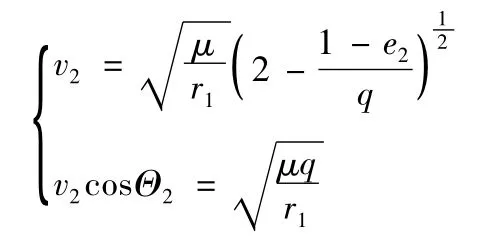
則初、終軌道的夾角

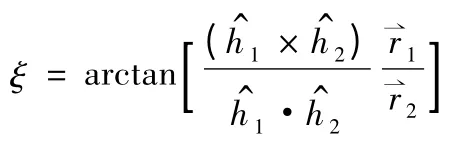
又已知Θ1為初始軌道彈道傾角

最終得到軌道坐標系下的Δv

2 改進遺傳算法思想及設計

為提高搜索的速度和搜索的精度，現對遺傳算法進行改進。由于遺傳算法的優點是全局搜索能力比較強，但它在局部搜索方面能力比較弱，搜索出的優化結果帶有隨機性，不一定能夠得到準確的全局最優解。又由于傳統的優化方法如梯度法、爬山法、方向加速法等都有很強的局部搜索能力，故將傳統的優化方法嵌入到遺傳算法中，使之能夠同時具有好的全局和局部搜索能力。

2.1 問題解的基因表示

顧及一組目標的情況下，基因表示為攔截器在獨立攻擊各個目標航天器的變軌時刻tm(m =1，2，…)及攔截時刻tmh(h=1，2，…)。由于此時編碼的范圍較大，且精度和運算速度要求都有所提高，所以這里選用浮點數編碼。

2.2 適應度函數

要求機動變軌到各個目標所耗能量累加最小為最優，故遺傳算法的適應度函數可表示為3，…。

約束條件為hi(X)≤0，i=1，2…，則設懲罰函數:

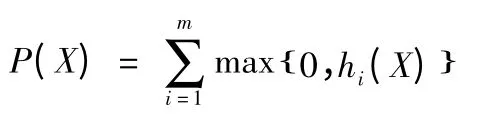
考慮懲罰函數后，廣義的適應度函數可以定義:

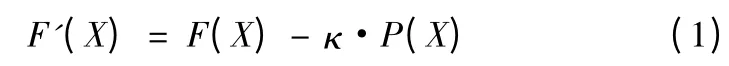
式(1)中，κ 為懲罰函數作用強度的系數，κ ＞0 且當κ→+∞時，廣義適應度函數將收斂到原問題的解。但在實際運算中，如果懲罰函數的強度太小的話，就有可能使個體的適應度差異不大，降低了個體之間的競爭力，從而影響遺傳算法的運行效率;懲罰函數的強度太大的話，部分個體又有可能破壞約束條件，不能保證優化所得到的個體一定是滿足約束條件的可行解，在此處取κ=1。

最后，在上述設置下，廣義適應度函數:

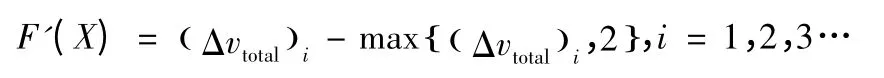
2.3 嵌入優化方法選擇

方向加速法具有很好的局部搜索功能，該方法不需要計算目標函數的梯度，且具有完善的理論體系，很適合本問題的優化。在已經完成遺傳操作的群體中選取某些個體應用方向加速法進行局部尋優，以優化后的結果作為新的染色體，能有效改善群體的性能。選取的數目越多，優化效果也就越好，但也會帶來計算量的加大，因此本節選取群體中適應度值較小的n 個個體進行計算。

2.4 遺傳操作

選擇算子。這里采用比例選擇法選取適應度值較小的個體以一定的概率遺傳至下一代。設群體的大小為M，個體i 的適應度為Fi，則個體被選中的概率pis:

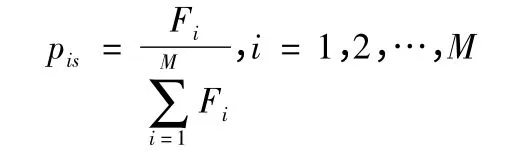
交叉算子。這里采用非均勻算術法，即設XkA，XkB為第k代的兩個個體，則經交叉運算后產生的兩個新個體:

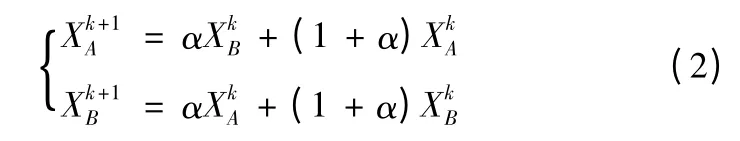
式(2)中，0 ＜α ＜1 隨著遺傳代數的增大，α 逐漸接近于0。

變異算子。這里采用非均勻變異法，即設X =x1x2…xk…xl為將要進行變異的個體，變異點為xk，xk處基因值的取值范圍為則新的基因值x'k的產生方法:

G 為當前的遺傳代數;R(G，y)為一產生非均勻隨機數的函數，隨機數的取值范圍為 [0，y]，且隨著G 的增大，R(G，y)接近于零的概率也逐漸增加。

3 停泊軌道優化解算流程

設計停泊軌道優化解算流程如圖2 所示。

圖2 停泊軌道優化解算流程

優化解算流程:

1)輸入空間攔截器及一組多個目標航天器的軌道數據。目標航天器軌道數據選定如表2 所示，攔截器初始軌道數據根據多次試驗結果獲得。

2)設定攔截器軌道參數變化值域及步長。這里根據文獻［7］中的結論，選定

3)在一次步長計算中，應用改進遺傳算法進行仿真優化，得到攔截器對各目標累加所需的當前步長最小速度增量

4)在攔截器軌道參數變化值域內進行所有步長的循環計算;

6)得到最終的攔截器停泊軌道數據。

4 仿真分析

下面根據文獻［7］中的結論擬合出一組目標軌道數據如表1 所示。

好的攔截器軌道初始值能有效節約搜索時間以及提高優化精度，此處根據多次試驗選取停泊軌道參數初始值為:a，e，i，Ω，ω，M=7 000 km，0.1，30°，30°，10°，0°根據不同目標的重要性選定權重系數，有方案1:δ1j=0.1，0.2，0.3，0.2，0.2;方案2:δ2j=0.1，0.1，0.3，0.2，0.3，則仿真結果如表2所示。