多維背包約束下單調(diào)非減下模函數(shù)最大值的貪婪算法

宮興榮，何尚錄，楊留猛

(蘭州交通大學 數(shù)理與軟件工程學院，蘭州 730070)

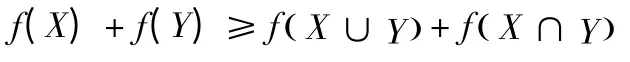
則稱f 是定義在Ω 上的下模集函數(shù). 又若對?X，Y∈Ω 且X?Y，f(X)≤f(Y)，則稱f 是單調(diào)非減的。

考慮如下組合最優(yōu)化問題:

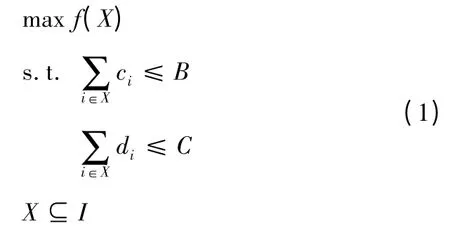
其中B，C，ci，di(i∈I))是非負整數(shù)，f(X)是非負非減的下模集函數(shù)。

上述問題屬于NP-難問題，沒有十分有效的求解方法，特別是多項式時間算法，于是人們主要研究求解此類問題的比較有效的近似算法。在求解組合最優(yōu)化問題的各種近似算法中，貪婪算法是最簡單且最為有效的算法.Nemhauseretal 考慮了單背包約束下ci=1(i∈I)的特殊情形，給出了一種簡單貪婪算法并證明了性能保證為1 - e-1。M.Suiridenko結合部分窮舉法與貪婪算法，給出了一般情形下單背包約束問題的一種改進的貪婪算法，并證明了其性能保證為1 -e-1。在此將這種情況中的思想推廣到多維背包約束的情形，給出求解問題(1)的貪婪算法，并證明了所給算法的性能保證為1 -e-1。所謂性能保證是指若由近似算法所求近似解至少是精確解的?倍，則稱此近似算法的性能保證為?。文中給出若干引理及其證明、問題(1)的近似算法，并證明了其性能保證。

1 若干引理及證明

引理2 單調(diào)非減的集函數(shù)f(X)是Ω 上的下模集函數(shù)當且僅當

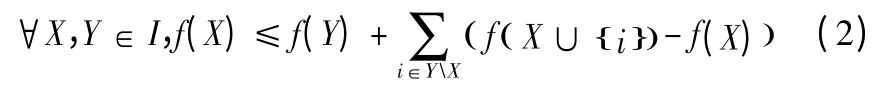
由f 是單調(diào)非減的下模集函數(shù)及引理1，得

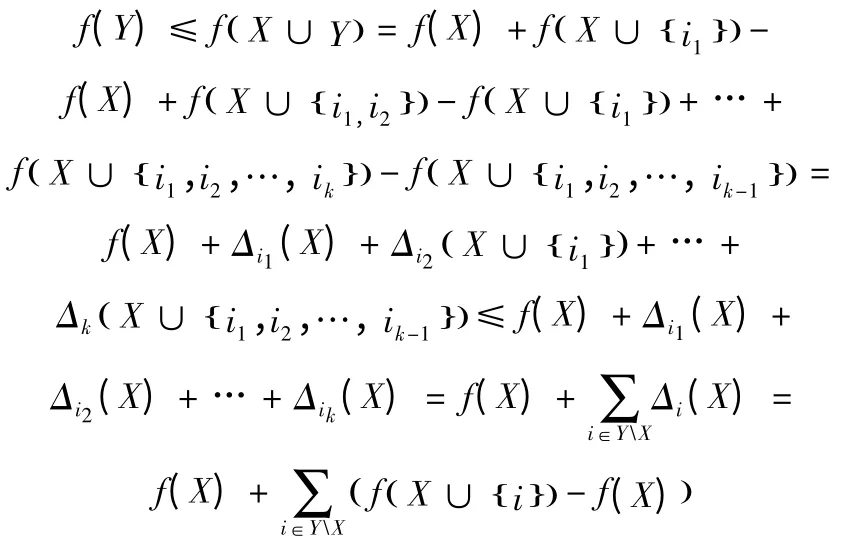
(充分性)設函數(shù)f 滿足不等式

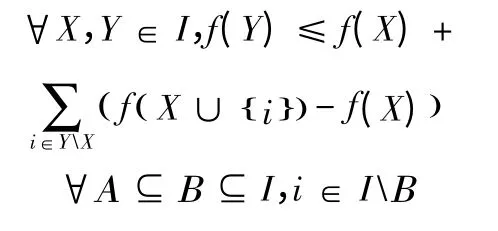
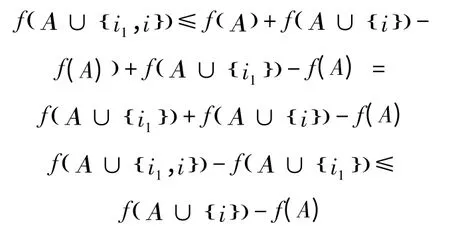
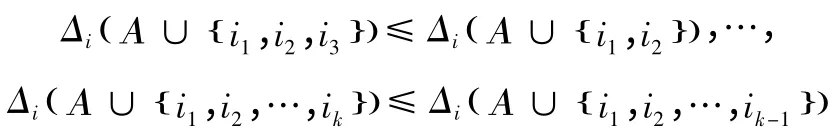
得到:

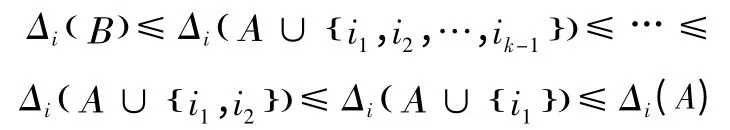
即對?Α?Β?I，i∈IΒ，有

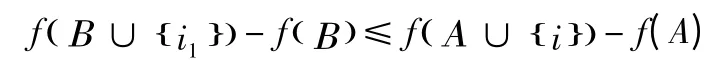
所以f 是Ω 上的非減的下模集函數(shù)。

引理3 設P，D 是任意正整數(shù)，ρi( 1，2，…，p )是任意非負實數(shù)，則有以下不等式

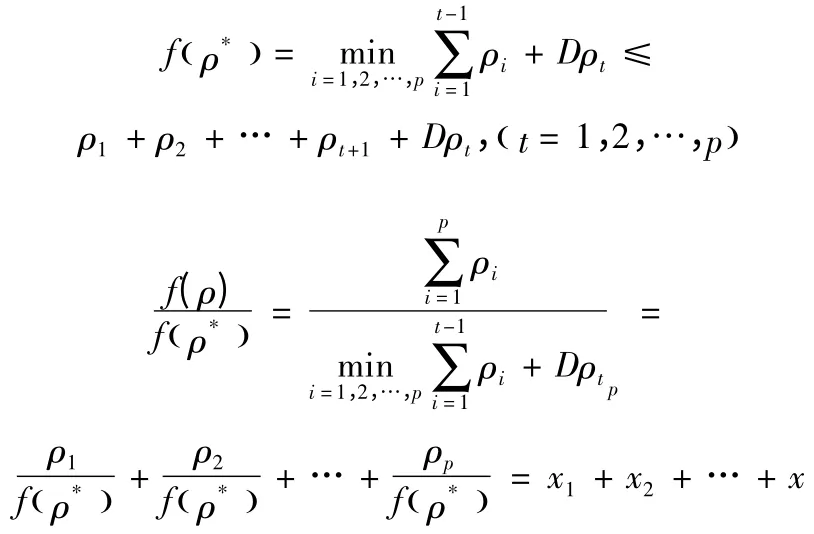
又由式(2)得

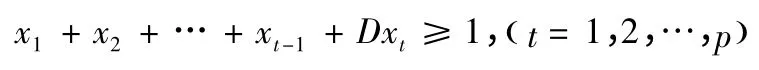
考慮如下線性規(guī)劃

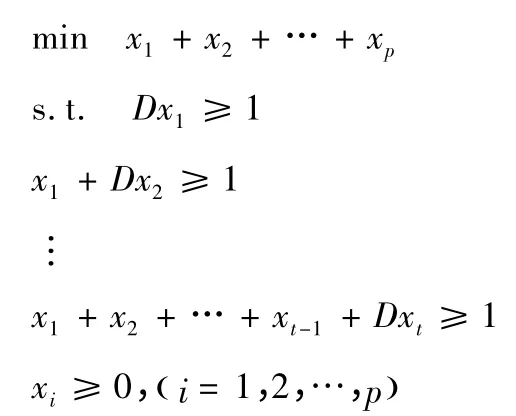
求得該線性規(guī)劃的可行解:

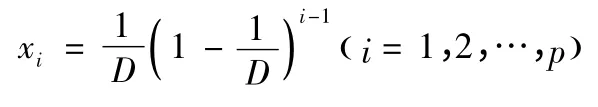
上述線性規(guī)劃的對偶規(guī)劃:

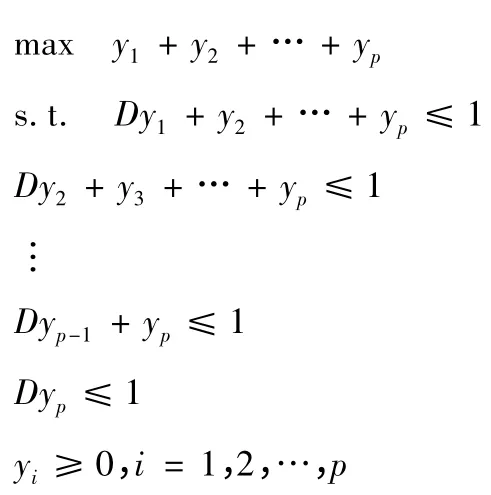
求得該對偶規(guī)劃的可行解:

不難看出這兩個線性規(guī)劃的最優(yōu)解相等，即有

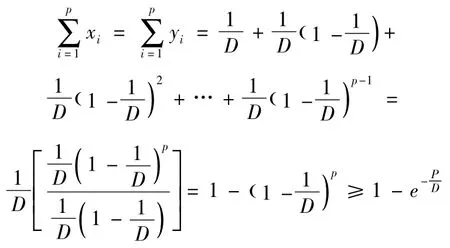
2 算法及其分析

2.1 基本思想

列舉出基數(shù)為1 或2 的所有可行解，找出使目標函數(shù)值取最大值的可行解(最優(yōu)解集)，用X1表示;考慮基數(shù)為3 的所有可行解，在保證當前可行解集在多背包約束下可行的情況下，找出使目標函數(shù)取最大值的集合，用X2表示;若f則輸出X1，否則輸出X2。

2.2 具體算法

(3)找出

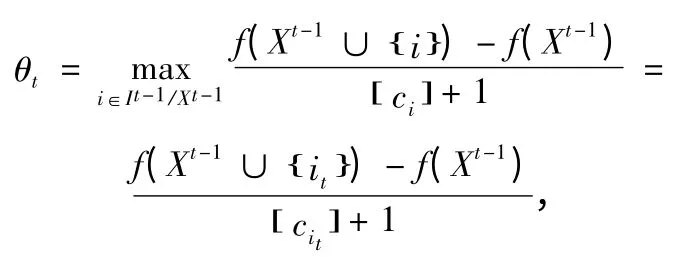
(4)若ItXt=?，終止，否則令t=t+1，轉(3);

(5)求出所有的由U 開始的Xt，并計算f(Xt)，

2.3 算法的時間復雜性

由于基數(shù)不超過3 的子集個數(shù)最多有3n3，故算法最多循環(huán)3n3次，而每次循環(huán)需調(diào)用一次貪婪算法求解，其復雜度為Ο(n)，故其算法的時間復雜度為Ο(n4)。

2.4 算法的性能保證

定理1:求解問題(1)的上述貪婪算法的性能保證是1-e-1。

證明:定義函數(shù)g(X)=f(X)-f(Y)，因f(X)是非減下模函數(shù)，故對?X 滿足Y?X?I，g(X)都是非減下模函數(shù)。因此g(X)滿足引理2 中的不等式(2)。

設t*+1 是算法中的不能將it*+1∈X*增加到Xt*中的第一步，則:Xt*+1=Xt*，It*+1=It* {it*+1} ，設t*+1 是從第t 步開始不能增加到Xt中的第一步，則:Xt= Xt-1，It=若

令Xt，t=1，2，…t*，是算法在第t 次迭代后所得的近似解。

根據(jù)不等式(2)及g(X)的定義有:

對t=1，2，…t*均成立。

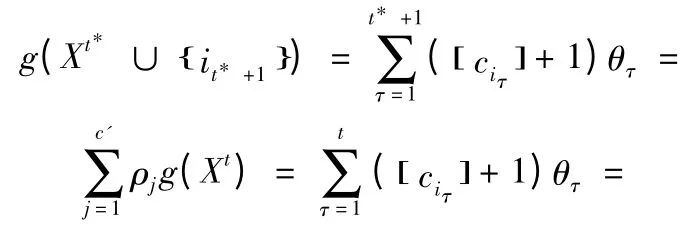
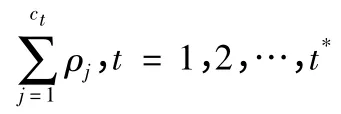
根據(jù)等式:

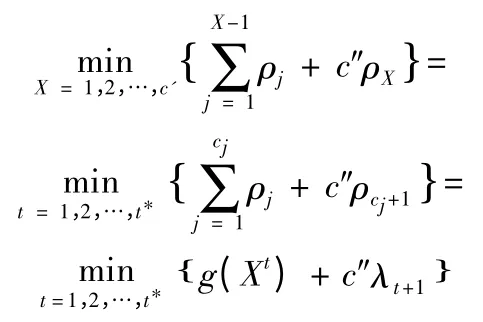
和不等(3)，(5)得:

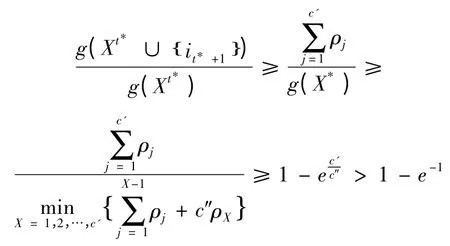
故即證得上述算法的性能保證為1 -e-1。

［1］ILEV V R. An approximation guarantee of the greedy descent algorithm for minimizing a submodular set function［J］.Discrete Applied M athematics，2001，114:131-146.

［2］SVIRIDENKO M.A note on maximi zing a submodular set function subject to a knapsack constraint［J］.OperationsResearch Letters，2004，32(2):41-43.

［3］羅亮，賈欣鑫，何尚錄.求解組合拍賣問題最大值的貪婪算法［J］.黑龍江科技學院學報，2008，18(5);382-384.

［4］雷習軍，趙杏利，李小平，等.求解背包約束下下模函數(shù)最大值問題的近似算法及其性能保證［J］.淮陰工學院學報，2010，19(3):15-18.

［5］李小平，趙杏利，雷習軍，等.求解下模福利問題的一種隨機算法及其性能保證［J］.蘭州交通大學學報，2011，30(1):139-141.