基于似然的航跡關聯算法研究＊

劉國棟 吳媛媛

（1.91550部隊 大連 116023）（2.海軍北海艦隊司令部 青島 266071）

1 引言

現有的用于航跡關聯的算法通常可以分為兩類：一類是基于統計的方法，另一類是基于模糊數學的方法［6～7］，本文提出了幾種基于似然的航跡關聯算法，它通過建立似然函數［9～11］來反映代表同一目標的不同傳感器間的航跡相似度，通過對似然函數的評估來決定一個最佳全局關聯假設，從而達到航跡關聯的目的。

2 問題的描述

我們對來自Ns個傳感器的航跡建立一個數學形式的描述，設每個傳感器上報的航跡數為Ti，i＝1，…Ns，那么第i個傳感器的航跡表示為Zj，i，j＝1，…Ti，對應的狀態估計為zj，i，協方差為Rj，i，定義一個集合量元組T，假設每個元組由來自同一個目標的狀態估計組成，這樣所有元組的組合就構成了一個全局的關聯假設H，一個元組對于一個傳感器最多只能包含它的一條航跡，且元組必須是非空的，所以每個元組的大小一定是限制在0＜NT≤Ns之間。

fi是來自傳感器i的航跡，如果一個元組中沒有航跡來自傳感器i，那么fi＝0，傳感器上報的每一條航跡都是一個元組的成員，且一條航跡只能在一個元組中，因此，在一個全局假設H中，所有元組的大小之和一定等于所有傳感器上報的航跡數之和，即

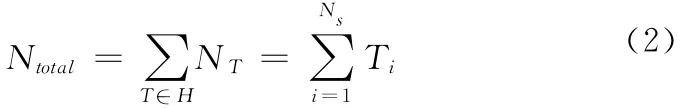
由于量測和過程噪聲的獨立，所以和不同目標關聯的航跡之間是獨立的，因此全局假設H的似然p（z1，1，…，可以分解為多個元組的似然，式（1）中定義的元組的似然可以表述為

這里L（T）為元組聯合概率密度函數，Pd代表傳感器的探測概率，且

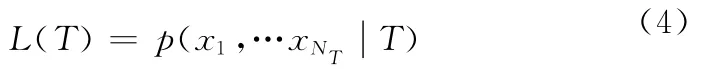
式（4）中的航跡觀測xi和協方差Ri，i＝1，…NT與航跡的狀態估計和誤差協方差是一一對應的，設所有的全局假設H構成的集合為W，則利用所有元組似然的乘積可以形成最大似然（ML）方法

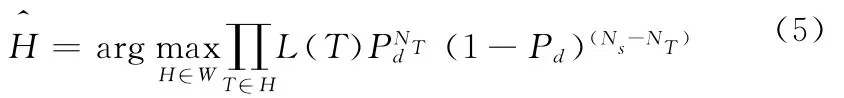
假設沒有虛警、漏警的理想情況（Pd＝1），這樣每個傳感器上報的航跡數就等于目標的總數，即N0＝T1＝…＝，ML方法可以簡化為

當來自不同傳感器的航跡源于同一目標時，ML方法是最優的，但是組成元組的航跡所對應的目標真實狀態往往是未知的，所以一個似然的精確表達式是難以獲得的，這就需要一些合適的似然近似來替代，本文將對四種元組似然的近似進行描述和分析，通過利用關聯誤差來達到對似然近似的目的。

為描述方便，下文將元組的大小NT統一表述為N，這樣一個元組中和不同航跡關聯的傳感器可記為i＝1，…N。對于第i個傳感器來說，xi是 M維目標狀態的估計，Rii是估計誤差協方差，一個元組中的N條航跡，狀態估計記為

這里si是來自第i個傳感器的真實目標狀態，ηi是狀態估計誤差，該誤差服從均值為0方差為Rii的高斯分布，由于共同的過程噪聲，來自不同傳感器同一目標的航跡之間存在互關聯，不妨設第i個傳感器和第k個傳感器對同一目標的互協方差為E｛ηiη′k｝＝Rik。在一個元組中認為N條航跡源于同一個目標，即有s1＝s2＝…＝sN＝s，所以式（7）可以簡化為

設XN是元組中N條航跡的串聯，即

對應的誤差協方差矩陣為

令NM×M維矩陣IN＝［IMIM…IM］′（11）

這里IM為M×M的單位陣。

對元組中的航跡進行融合，從而得到融合航跡

這里Rf，N是融合航跡的協方差

通常情況下，認為航跡間誤差是相互獨立的，即Rik＝0，i≠k，這樣式（12）、（13）可以簡化為

3 近似似然航跡關聯

3.1 順序似然

為討論問題的方便，認為航跡間的互協方差為零。

元組順序似然的表達式為

對于一個元組來說，當元組似然達到最大時，認為元組中對應的航跡源于同一個目標，利用該準則可以對不同傳感器的航跡進行有效的關聯，下述幾種似然均是采用此關聯準則。

圖1給出了順序似然的流程圖。

圖1 順序似然流程圖

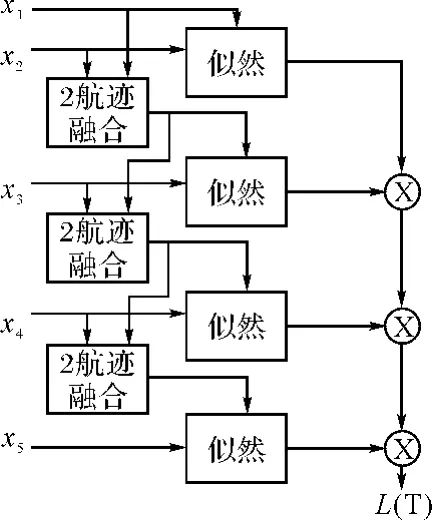
圖2 分布先驗似然的順序形式（N＝5）

圖中每個似然的輸入xi代表傳感器的航跡，順序似然可以通過一系列的最優2維分配來實現，首先，對來自傳感器1和2的航跡通過2維算法進行關聯，保持關聯結果固定，然后對來自傳感器2和3的航跡進行關聯，保持關聯結果固定，這樣重復，一直到來自傳感器N－1和N的航跡進行關聯，最后由各個2維關聯結果的乘積得到N維關聯結果，即順序似然。各個2維關聯之間可以獨立進行，然而該方法不是最優的，因為它依賴于各傳感器航跡序列的順序。

3.2 全局似然

全局似然的表達式為

式（17）中的指數2／N是對全局似然維度的歸一化，使之與順序似然的維度相一致，全局似然不依賴于航跡序列的順序，但它和順序似然一樣，都認為航跡誤差是相互獨立的。

4 仿真分析

為了討論問題的方便，這里均考慮三個局部節點的情況，且認為誤差互協方差均為零。

仿真環境1：三部雷達測距和測角誤差均為σρ＝170m，σθ＝1°，用蒙特卡洛方法進行50次仿真，每次仿真14步，采樣間隔T＝4s，假設在兩傳感器的公共觀測區域內有60批目標，模擬目標在一個二維平面上具有變速、存在有意和無意機動，具有可以認為在速度上變化的過程噪聲，目標初始速度在4m／s～1200m／s之間均勻分布，初始航向在0～2π之間均勻分布，目標初始位置在x＝190km，y＝135km處按正態分布產生，三局部節點的位置分別為（125km，125km）（235km，130km）、（190km，160km）。

在模擬目標運動時，取

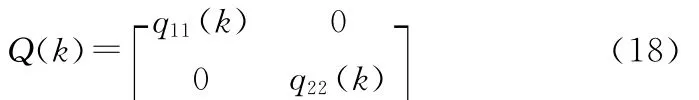
仿真結果1：

圖3 60批密集目標的運動軌跡

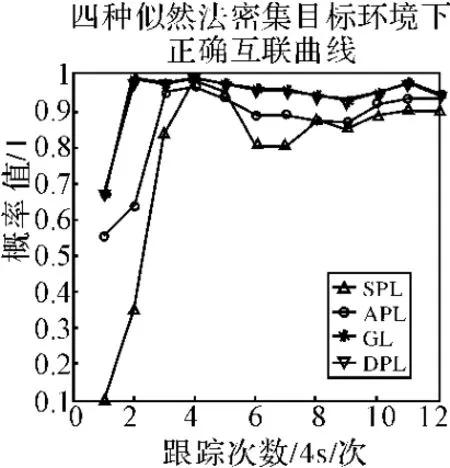
圖4 四種似然法正確關聯率對比

仿真分析1：圖3給出了在公共觀測區域60批密集目標的運動軌跡及三個局部節點的位置。圖4給出的是對圖3所示的公共區域目標的航跡分別采用兩種基于似然的航跡關聯方法仿真50次后的平均正確關聯率曲線，由圖4可以看出在密集目標環境下廣義似然和分布先驗似然有較好的正確關聯效果，并且這兩種方法的關聯效果幾乎一致，全局似然的正確關聯效果次之，但也能維持較高的正確關聯率，順序似然的正確關聯效果最差，全局似然正確關聯率高于順序似然的原因在于它合并了所有的兩兩航跡間的聯合，而順序似然只是合并了順序兩兩航跡間的聯合。由仿真結果可以看出這兩種基于似然的航跡關聯算法均能達到較好的關聯效果，只是順序似然在關聯初始階段稍差。

仿真環境2：三部雷達測距和測角誤差均為σρ＝100m，σθ＝0.6°用蒙特卡洛方法進行50次仿真，每次仿真14步，采樣間隔T＝4s，假設在兩傳感器的公共觀測區域內有N＝10批目標，模擬目標在一個二維平面上做勻速直線運動，具有可以認為在速度上變化的過程噪聲，目標速度為vx＝600m／s，vy＝600m／s，目標初始位置在x＝－8km，y＝－15km附近產生，目標之間的間距設為d＝200m，三局部節點 的 位 置 分 別 為 （125km，125km）（235km，130km）、（190km，160km）。

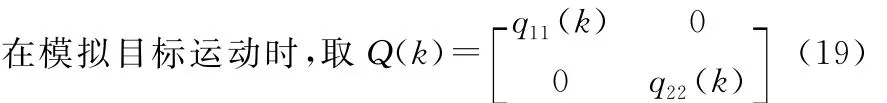
仿真結果2：

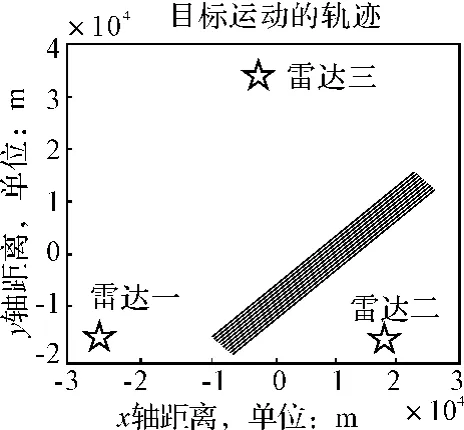
圖5 10批平行目標的運動軌跡

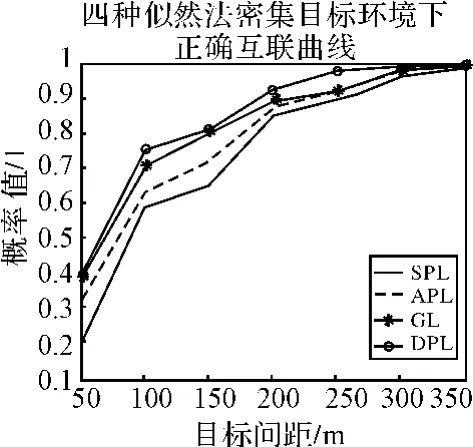
圖6 兩種似然法正確關聯率隨目標間距變化比較圖

仿真分析2：圖5給出了在公共觀測區域10批平行目標的運動軌跡及三個局部節點的位置。圖5給出的是對圖6所示的公共區域目標的航跡分別采用四種基于似然的航跡關聯方法仿真50次后的平均正確關聯率隨目標間距變化曲線，由圖6可以看出在平行目標環境下，兩種似然關聯算法正確關聯率均是隨著目標間距的增大而增大，其中在相同目標間距的情況下，分布先驗似然的關聯效果最優，廣義似然、全局似然和順序似然的關聯效果依次次之，并且均能達到較好的關聯效果。

5 結語

本文先對似然關聯進行了簡單的問題描述，接著給出了兩種基于似然的航跡關聯算法，這兩種算法通過建立似然函數來反應航跡間的相似程度，從而達到航跡關聯的目的，最后通過兩種典型仿真環境下的仿真結果可以看出，基于似然的航跡關聯算法對密集目標和平行目標均能達到較好的航跡關聯效果。

［1］Chen，H.，Kirubarajan，T.，and Bar－Shalom，Y.Performance limits of track－to－track fusion versus centralized estimation：Theory and application.IEEE Transactions on Aerospace and Electronic Systems，39，2（Apr.2003）：386－400.

［2］Chong，C.－Y.，Mori，S.，Barker，W.H.，and Chang，K.－C.Architectures and algorithms for track association and fusion.IEEE Aerospace and Electronic Systems Magazine，15，1（Jan.2000）：5－13.

［3］Rao，B.S.，and Durrant－Whyte，H.F.Fully decentralized algorithm for multisensor Kalman filtering.IEEE Proceedings，Pt.D，138，5（1991）：413－420.

［4］Bar－Shalom.Y.， William.D.B.， Multitarget－Multisensor Tracking，Applications and Advances［M］.Artech House，2001：155－157.

［5］Bar－Shalom.Y.A Tutorial on Multitarget－Multisensor Tracking and Fusion.1997，IEEE National Radar Conference，15 May 1997，Syracuse，NY.

［6］何友.分布式多傳感信息融合算法研究［D］.清華大學，2006.

［7］何友，王國宏，陸大金，等.多傳感器信息融合及應用［M］.（第二版）.北京：電子工業出版社，2000：203－206.

［8］李啟元，段立，李亞楠.海戰場目標航跡間距離聚類方法［J］.計算機與數字工程，2010（5）.

［9］Blackman，S.S.，and Popoli，R.Design and Analysis of Modern Tracking Systems.Boston：Artech House，1999：7－14.

［10］Bar－Shalom.Y.，and Chen，H.Multisensor track－to－track association for tracking with dependent errors.ISIF Journal of Advances in Information Fusion，1（July 2006），3－14.

［11］Pattipati，K.R.，Kirubarajan，T.，and Popp，R.L.Survey of assignment techniques for multitarget tracking.In Y.Bar－Shalom and W.D.Blair（Eds.）， Multitarget－Multisensor Tracking：Applications and Advances，vol.3.Norwood，MA：Artech House，2000：77－159.