單斜熱絲測量三維速度場算法研究

鐘 明，陳洪敏，熊 兵，田 偉，吉建波

(1.中國燃氣渦輪研究院，四川江油621703；2.柴油機高增壓技術國防科技重點試驗室，山西大同037036)

1 引言

隨著對各種流動現象研究的深入，對流動測量技術的要求也越來越高。三維速度場測量已發展了熱線、LDV、PIV等多項技術，這些技術原理各異、性能有別，適用范圍不一，其中熱線技術因其測試系統簡單、頻率響應寬、測量精度高等優點而得到廣泛應用[1]。熱線技術測量三維速度場時，可用三絲探頭或單斜熱絲探頭。但三絲探頭有六根支桿，所占體積較大，很難分辨小尺度空間的強剪切流，且探頭對流場干擾較大，校準復雜，維修費用高。單斜熱絲探頭因對流場干擾較小、空間分辨率較高、使用方便，在實際應用中得到更多重視[2]，但存在校準困難，數據處理復雜、耗時長等。單斜熱絲測量技術的測量精度和范圍，取決于能否有效地反映單斜熱絲對氣流速度(大小和方向)的敏感性。本文根據經驗關系式，提出以改進的粒子群優化算法(PSO)求解實際測量流場數據，并通過試驗驗證算法的有效性。

2 三維速度場的單斜熱絲測量方法

用單斜熱絲測量三維流場是基于熱絲的方向敏感性。當氣流不垂直于熱絲時，熱絲所感受的冷卻速度(有效速度)為氣流速度和方向的函數，其關系如圖1所示。圖中，V為冷卻速度，U為輸出電壓，θy為偏轉角，θp為俯仰角。

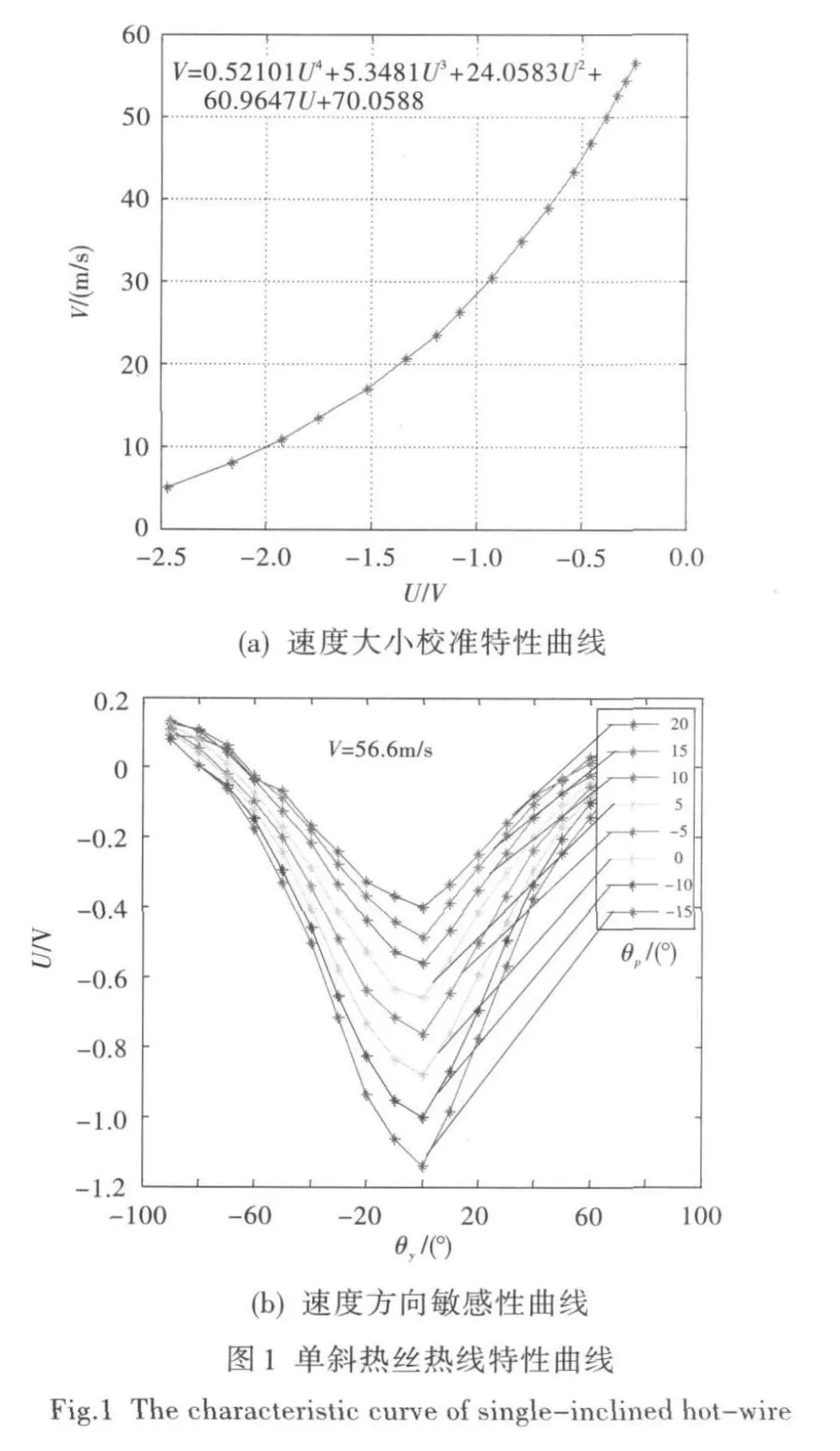
針對單斜熱絲對氣流速度的敏感性，本文采用下列經驗關系式表示：

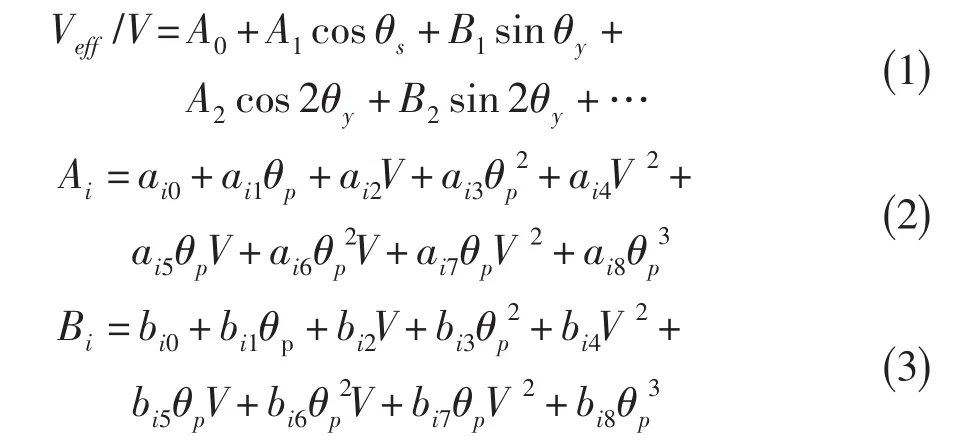
式中：Veff為有效速度，θs為單斜熱絲傾角，三角函數的階數一般取3～4階，系數aij和bij由最小二乘法擬合校準數據確定。由于熱絲的方向敏感性對θy＝0°不對稱，通常把校準角度分為對稱的兩組，-90°≤θy≤0°和0°≤θy≤90°，分別對這兩組偏轉角用最小二乘法擬合出上式中的校準系數。實際測量中要得到三維速度值，需將單斜熱絲放置在不同角度位置，當熱絲繞自身軸線旋轉時，僅氣流對探針的偏轉角改變，俯仰角不變。如果探針只旋轉三個位置進行測量，理論上可求解方程組，但由于校準曲線由最小二乘法擬合得到，求解誤差較大[4]。當氣流俯仰角變化范圍較寬時，增加探針角向測量位置，可有效提高測量精度，一般選取5～7個測試點，可表示為：

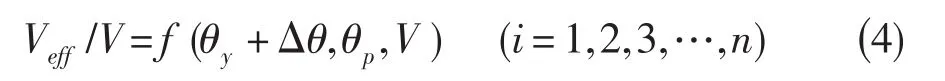
用上式對各種測試數據進行擬合，構成一個非線性最小二乘問題，即確定目標函數使上式理論值與實際值誤差最小的解(V ，θp，θy)。對此，文獻[4]提出用最小二乘算法求解，文獻[5]提出用非線性最優化的L-M算法進行數據處理。雖然這兩種算法求解速度快，但都要求擬合函數能方便地分解為矩陣形式，公式(1)～(3)求解函數復雜，很難分解為矩陣形式，因此這兩種算法求解困難。另外，由于實際測量時速度主流方向的不確定性，熱絲旋轉的不同角度數據如果根據角度偏轉正負帶入公式計算，必然引入熱絲方向敏感性不對稱誤差，使得前面分組校準失去意義。角度的不確定性如圖2所示。

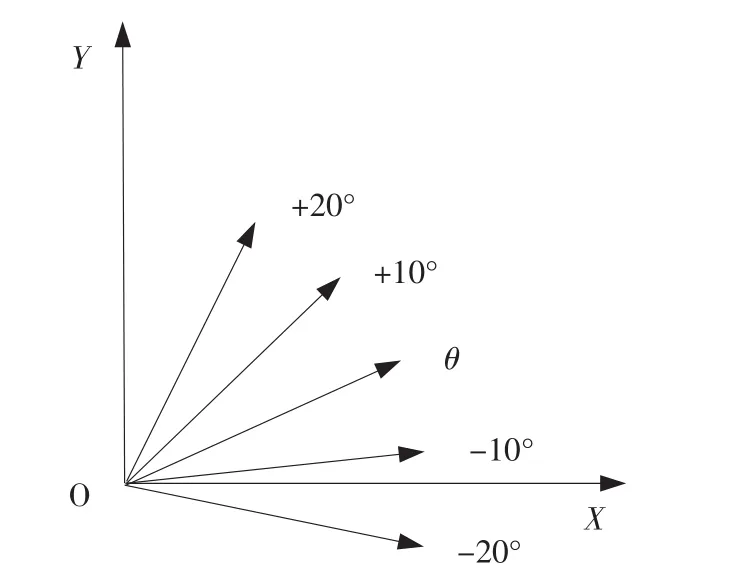
圖2 偏轉角度的不確定性Fig.2 The uncertain characteristic of pitch angle

針對以上問題，本文利用改進的粒子群優化算法求解上述非線性最小二乘問題，不需對公式進行矩陣分解，且有效解決了起始角度(零位)不確定性問題(熱線零位指氣流主流方向)，避免了實際測量計算時引入方向不對稱性誤差，提高了測量精度。

3 粒子群優化算法流程

粒子群優化算法是一種智能優化算法[6]，一旦確定了其微粒子和適應度函數，則函數優化問題的計算步驟可總結為：

(1)隨機初始化粒子群的位置和速度，其位置和速度應在限制范圍內。

(2)執行粒子群算法。粒子在迭代時，根據經典粒子群算法迭代方程更新自己的速度和位置，慣性權重系數ω按下式更新：

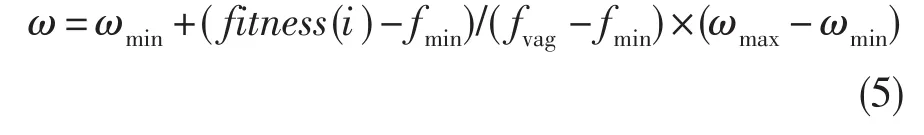
式中：fvag、fmin分別為適應度函數的平均值和最小值，ωmax、ωmin分別為慣性權重的最大值和最小值，fitness(i)為個體的適應度函數。

(3)計算粒子個體的適應度函數。如果粒子適應度優于個體極值的適應度，則更新個體極值Pb；如果有個體適應度值優于全局極值的適應度，則更新全局極值Pg。

(4)粒子個體采用變異因子進行變異，計算變異后個體的適應度并更新個體極值和全局極值。

(5)判斷適應度值是否滿足精度或是否達到最大迭代數，如滿足要求則結束并輸出結果，否則返回步驟(2)繼續迭代。

4 驗證試驗分析

為掌握單斜熱絲測三維流場的技術，驗證算法的有效性，通過熱線風速儀對壓氣機轉子出口流場的測試，研究不同狀態下壓氣機轉子出口的三維流動結構，并分析算法的性能。測量站布置在轉子出口測量截面距葉尖尾緣約15.0%弦長處，葉根到葉尖共分25站測量，近葉根6站和近葉尖6站，站間徑向間距為2.5%葉高(5 mm)，葉中測量13站，站間距為5.0%葉高(10 mm)。記錄單斜熱絲探針旋轉7個角度的數據。定義適應度函數為7組測量數據經驗公式計算值Vi與粒子速度值Vi′誤差的累積平方和：

粒子群隨機產生的初始偏轉角即為探針旋轉的初始角度θ，記錄的7組數據分別對應為θ+30°，θ+20°，θ+10°，θ，θ-10°，θ-20°，θ-30°的有效冷卻速度(±代表熱線探針相對初始位置的左右旋轉)，公式計算值Vi根據偏轉角(θ±Δθ)的正負將相應的校準系數代入經驗公式計算得出。相對坐標系下部分試驗結果如表1所示。

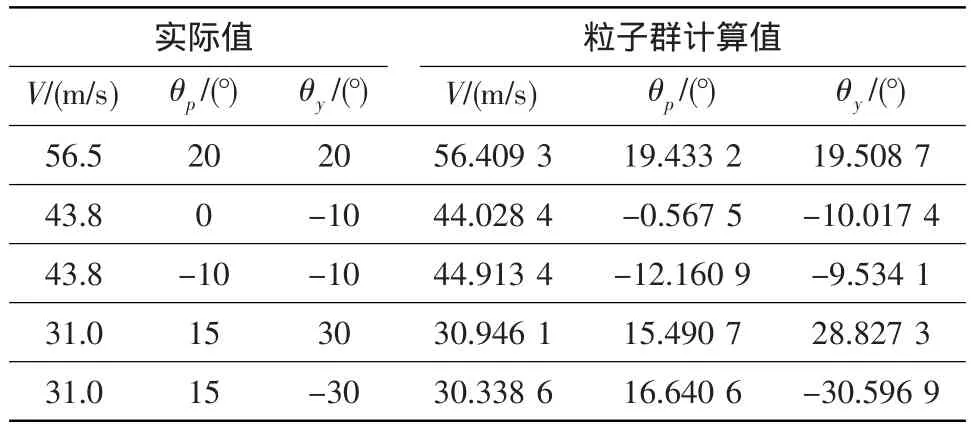
表1 粒子群算法計算結果Table 1 The calculation results ofparticle swarm optimization

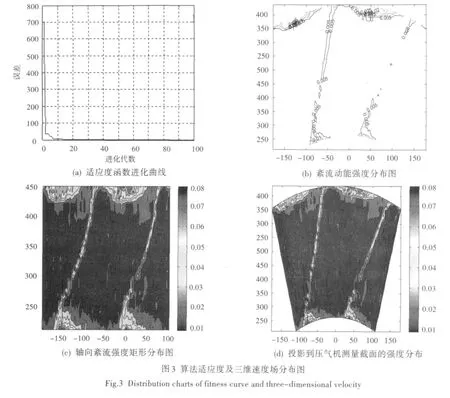
圖3為算法適應度及壓氣機轉子出口三維速度場分布圖。由圖3(a)中可知，粒子群算法適應度能很快進化到最優。單斜熱絲校準數據對該算法的校準結果(表1)也表明，算法搜索結果收斂精度較高，速度誤差在1.5 m/s內，角度誤差在±2°內，證明采用粒子群優化算法能有效克服試驗中單斜熱絲熱線旋轉帶來的角度不確定性影響，避免了由熱線方向敏感性帶來的方向誤差。圖3(b)是壓氣機測量截面的紊流動能分布圖，圖3(c)是軸向紊流強度的矩形分布圖，通過圖像投影算法將熱線測量速度數據在壓氣機測量截面重建(圖3(d))，可直觀看出壓氣機截面速度場分布，清晰了解沿葉高速度場的變化規律。

5 結束語

單斜熱絲測量三維速度場主要利用熱絲對氣流速度的敏感性，其測量精度取決于算法能否在較大速度和角度范圍內準確有效地反映有效速度與氣流大小和方向的關系。本文根據某單絲熱線的速度、方向敏感性經驗關系式，在分析最小二乘、L-M算法不足的基礎上，采用粒子群優化算法求解測量數據，有效解決了熱線旋轉角度不確定性問題，避免實際計算時重新引入熱線方向性誤差，試驗結果表明該算法有較好的精度。同時，采用圖像重建技術將數據轉化為速度場分布圖，可清晰直觀地呈現出壓氣機出口截面的流場分布。但粒子群優化算法收斂時間比最小二乘法長，因此在大量數據的處理中時間復雜度高、耗時長，不適合試驗數據的在線分析。如何分析參數設置對粒子群算法的影響，及進一步提高算法精度和減小時間復雜度，需做進一步研究。

[1]鄧康耀，顧宏中，鄔靜川.應用熱線風速儀測試二維周期性非定常流動[J].流體力學試驗與測量，1998，12(2)：80—83.

[2]盛森芝，徐月亭，袁輝靖.熱線熱膜流速計[M].北京：中國科學技術出版社，2003.

[3]馬宏偉，蔣浩康.單轉子壓氣機設計狀態和近失速狀態出口三維紊流流場[J].工程熱物理學報，1997，18(2)：153—158.

[4]李雨村，蔣浩康.單斜熱絲測量葉輪機內三維流動[J].航空動力學報，1989，4(2)：145—149.

[5]郭恩民，李志剛.葉輪機械中三維周期性非定常流場測量[J].航空動力學報，1998，13(3)：241—244.

[6]鄒 毅，朱曉萍，王秀平.一種混沌粒子群混合算法研究[J].沈陽工程學院學報，2009，5(3)：258—260.