基于遺傳算法的發(fā)動機氣路性能模型修正研究

李 冬，王冠超，曹明川

(1.海軍航空工程學院研究生管理大隊，山東煙臺264001；2.海軍駐長春地區(qū)航空軍事代表室，吉林長春300000)

1 引言

通常根據(jù)發(fā)動機的額定特性來建立發(fā)動機的數(shù)學模型，忽略了不同發(fā)動機之間的性能差異和使用過程中的性能蛻化。因此，計算出的發(fā)動機性能參數(shù)與發(fā)動機實際性能參數(shù)存在較大誤差[1]。加之發(fā)動機各部件特性為單獨得到，而發(fā)動機作為一個整體共同工作，即使所得各部件特性十分精確，但各部件間的相互影響和一些隨機因素的干擾，使得各截面的特性參數(shù)及發(fā)動機輸出的性能參數(shù)也不盡相同，因此有必要對模型進行修正。發(fā)動機穩(wěn)態(tài)模型的修正過程在一定程度上即為模型參數(shù)的優(yōu)化過程。遺傳算法(GA)作為一種新的智能算法，采用人工進化的方式對目標空間進行隨機搜索[2]，在參數(shù)尋優(yōu)方面有其獨特優(yōu)勢。基于此，本文采用遺傳算法作為模型修正算法。利用相關性分析確定部件修正參數(shù)(發(fā)動機部件特性參數(shù))和目標性能參數(shù)(發(fā)動機整機性能表征參數(shù))作為模型修正基礎，在求解發(fā)動機穩(wěn)態(tài)性能模型六個平衡方程的基礎上[3]，構造發(fā)動機性能模型修正代價函數(shù)，完成對發(fā)動機穩(wěn)態(tài)模型的修正；計算了幾種不同工況的發(fā)動機修正前后的特性參數(shù)，并將修正后的特性參數(shù)與用影響系數(shù)矩陣方法[4]所得修正結果進行對比；進一步討論了利用不同部件修正參數(shù)組合修正發(fā)動機穩(wěn)態(tài)模型。

2 發(fā)動機性能模型修正代價函數(shù)的構建

在發(fā)動機穩(wěn)態(tài)模型基礎上，用誤差向量E={εi,i=1,…,6}構造代價函數(shù)，用ai表示大于零的權系數(shù)，構造求解發(fā)動機穩(wěn)態(tài)模型的代價函數(shù)[5，6]：

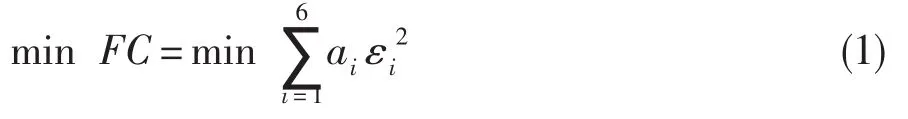
當模型計算輸出值與設計值誤差較大時，引入部件修正因子(定義為k=Ve/Vm，其中Vm、Ve分別為發(fā)動機各部件的設計參數(shù)值和修正后的參數(shù)值)。

發(fā)動機穩(wěn)態(tài)模型修正思路為，通過選擇合適的k，將發(fā)動機性能計算模型中的Vm用kVm替代，而使模型計算值與發(fā)動機設計參數(shù)值相一致。則式(1)可進一步描述為：

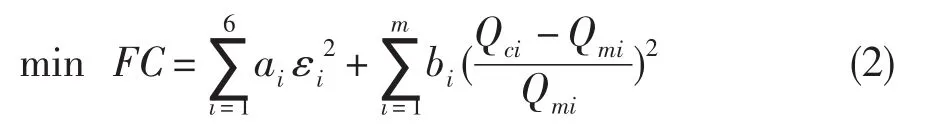
式中：F C表示預測性能參數(shù)值和設計性能參數(shù)值的差異，bi為大于零的權系數(shù)，Qmi為發(fā)動機設計第i個參數(shù)值，Qci為相應發(fā)動機模型第i個計算結果。式(2)也可表示成求解發(fā)動機穩(wěn)態(tài)模型初始變量xi和修正因子kl的函數(shù)[7]：

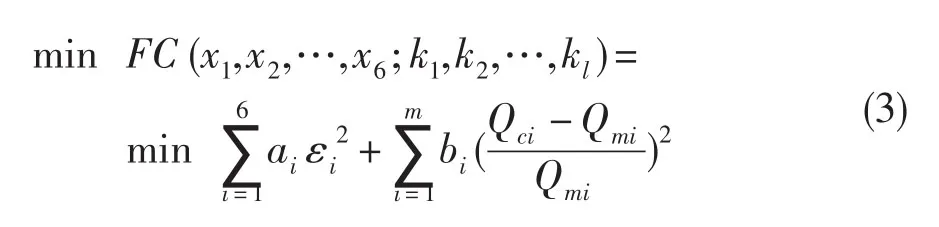
式中：l為修正因子向量維數(shù)，m為發(fā)動機參數(shù)設計值與模型計算值誤差向量維數(shù)。

值得注意的是，很多時候l和m并不相等。并且在式(3)滿足最小值要求下，l＞m時kl(1,2,…,l)存在無窮個解；l≤m時kl(1,2,…,l)存在唯一的最小二乘解，且只有l(wèi)=m時式(3)的最小值為0，其它情況則不然[8]。為提高模型修正精度，本文只考慮l=m的情況。

3 性能模型修正因子的優(yōu)化選擇

3.1 修正因子選擇原則[9]

恰當選擇部件修正參數(shù)對自適應模型求解十分重要。在選擇待修正的部件參數(shù)時，需考慮以下幾個重要因素：

(1)所選擇的部件修正參數(shù)必須與目標性能參數(shù)有很強的關系，否則在自適應修正過程中沒有足夠的搜索空間，不能搜索到更優(yōu)的修正結果。

(2)部件修正參數(shù)個數(shù)沒有限制，但修正參數(shù)選擇不同會導致修正效果不同；部件修正參數(shù)個數(shù)選擇越多，搜索空間越大，所獲得的修正結果就越接近目標參數(shù)。

(3)部件修正參數(shù)的上下限同樣決定了搜索空間范圍，因此在自適應修正過程中，選擇參數(shù)合適的上下限十分重要，這可能需要多次試驗來確保最優(yōu)值包含在搜索空間中。

3.2 優(yōu)選性能模型修正因子

就發(fā)動機安裝工藝而言，風扇、壓氣機、渦輪葉片的制造公差和裝配工藝偏差是造成單臺發(fā)動機試車參數(shù)不一致的主要因素，從而導致風扇、壓氣機和渦輪等核心機部件的特性線產(chǎn)生差異。根據(jù)上述分析，確定風扇流量Wa22、風扇效率ηcL、風扇增壓比πcL、高壓壓氣機流量W3、高壓壓氣機效率ηcH、高壓壓氣機增壓比πcH、高壓渦輪流量Wst45、高壓渦輪效率ηTH、低壓渦輪流量Ws t5和低壓渦輪效率ηTL作為發(fā)動機部件修正參數(shù)選擇對象。考慮到實際情況與參數(shù)測量難易，確定目標性能參數(shù)為高壓壓氣機出口壓力P3、低壓渦輪出口溫度T5、尾噴口出口溫度T8、發(fā)動機推力F和耗油率sfc。

發(fā)動機某個部件特性參數(shù)變化，可能對發(fā)動機某些截面測量參數(shù)輸出量影響較大，而對另一些輸出量影響較小；而某個截面參數(shù)輸出量變化，可能由若干部件特性參數(shù)的變化引起。利用相關性分析方法，找出部件修正參數(shù)的最佳組合作為發(fā)動機模型修正基礎。這里定義相關系數(shù)為：

在相關性分析前，首先求出發(fā)動機部件修正參數(shù)與目標性能參數(shù)間的相關系數(shù)。基于此，本文利用單個部件修正參數(shù)擾動法，即依次將部件修正參數(shù)減少2%，同時保持其余部件修正參數(shù)不變，計算發(fā)動機特性參數(shù)。其結果見表1。

由于相關性分析的目的是找出對每個目標性能參數(shù)影響最大的部件修正參數(shù)。為便于分析，應對相關系數(shù)進行歸一化處理。按列進行歸一化處理，歸一化相關系數(shù)計算式為：

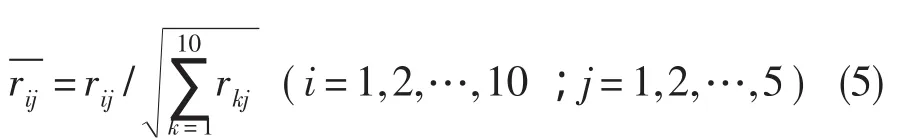
歸一化后的相關系數(shù)見表2。其中，相關系數(shù)大于0.5可認為是強相關，在0.3～0.5之間為中等相關，小于0.3的為弱相關。由此可看出，表中相關程度基本為弱相關，但具體數(shù)值不同。針對此情況，繼續(xù)構造參數(shù)優(yōu)選指標(敏感系數(shù))：

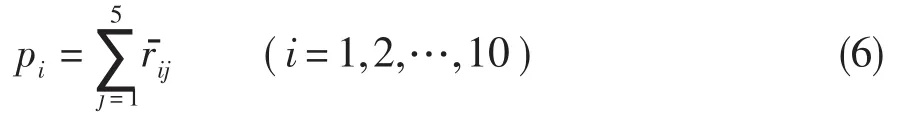
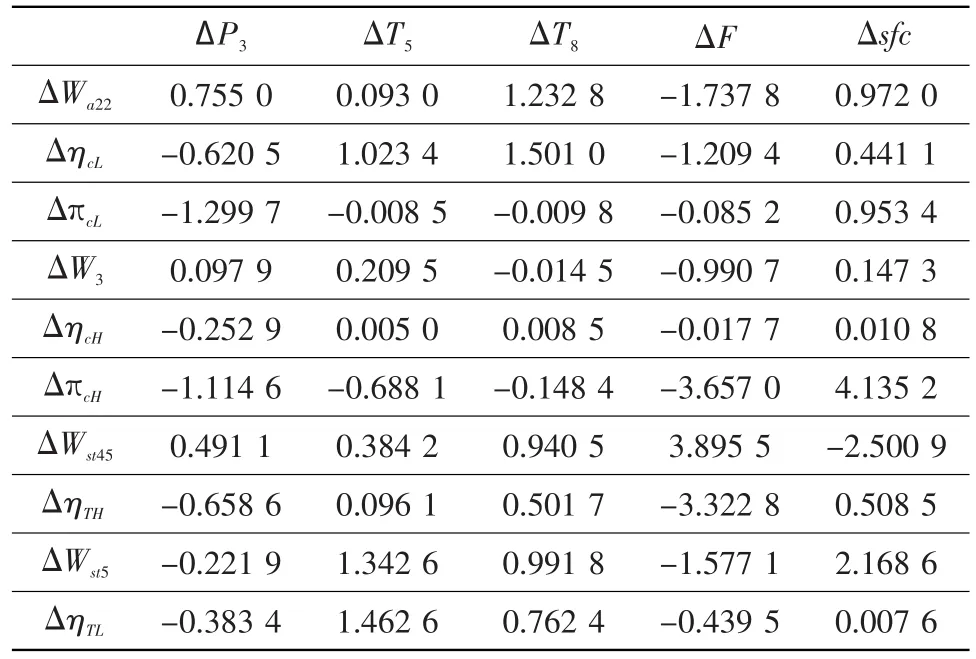
表1 部件修正參數(shù)減少2%后目標性能參數(shù)的變化 %Table 1 Variation of objective performance parameters when decreasing 2%of each component modified parameter

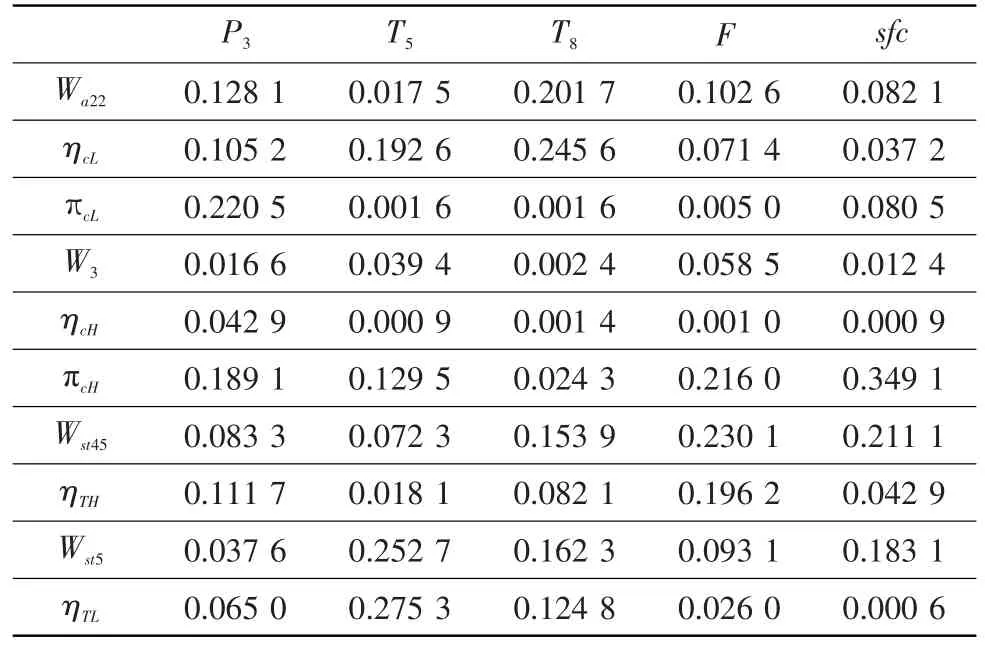
表2 歸一化后的相關系數(shù)表 %Table 2 Related coefficients after normalization

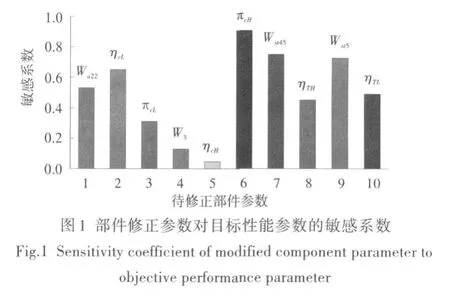
圖1示出不同部件修正參數(shù)的敏感系數(shù)。同時，為比較分析不同參數(shù)組合對穩(wěn)態(tài)模型的修正結果，選取有代表性的三組數(shù)據(jù)：第一組敏感系數(shù)排在前五的部件修正參數(shù)，即Wa22、ηcL、πcH、Wst45、Wst5；第二組排在后五的部件修正參數(shù)，即 πcL、W3、ηcH、ηTH、ηTL；第三組為排在中間的五個部件修正參數(shù)，即Wst45、Wst5、πcL、W3、ηcH。此時，選取的部件修正參數(shù)與目標性能參數(shù)數(shù)目一致，故kl(1,2,…,l)有唯一解。

4 基于遺傳算法的發(fā)動機模型修正

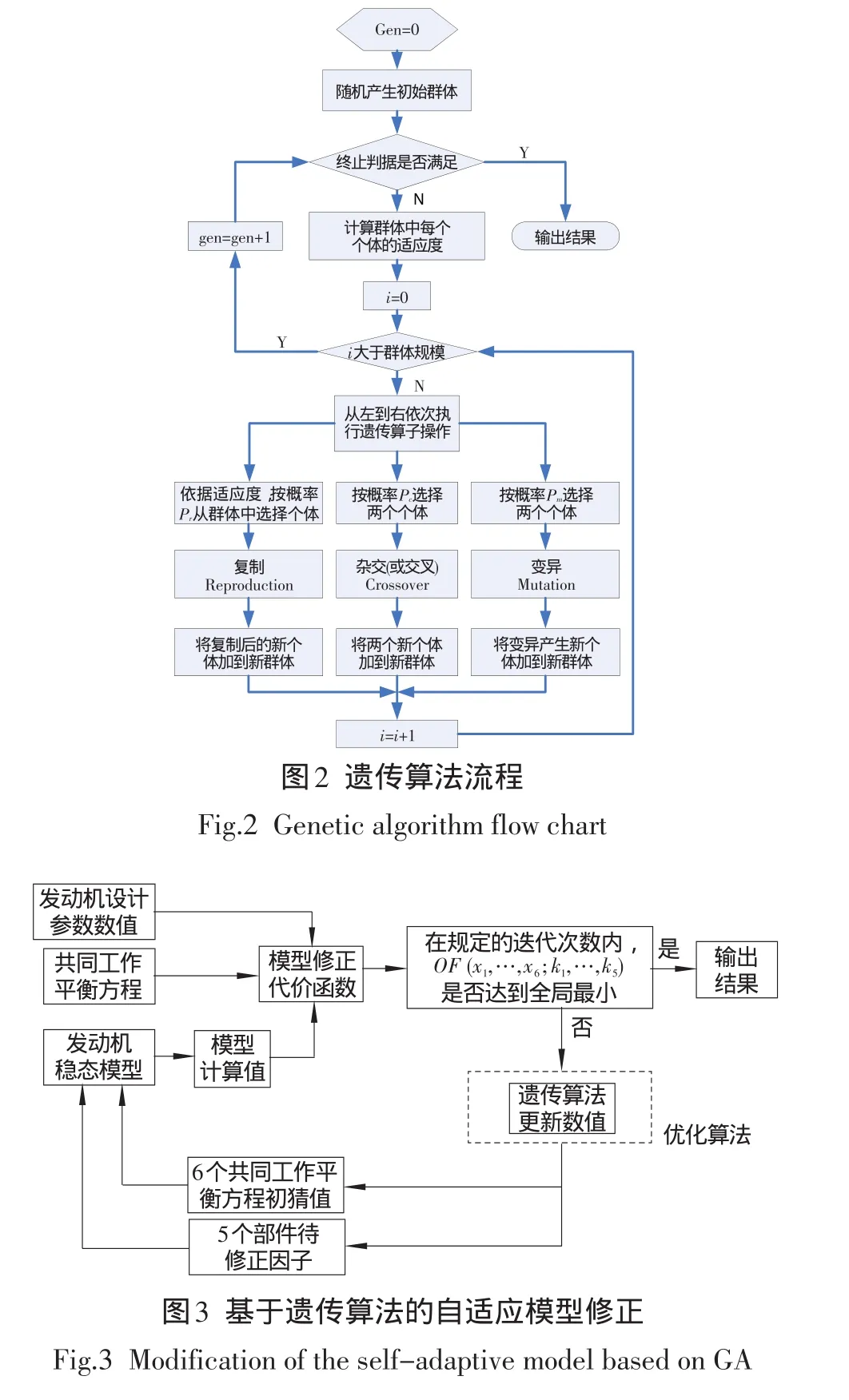
遺傳算法的算法流程如圖2所示，基于遺傳算法的發(fā)動機穩(wěn)態(tài)模型修正過程如圖3所示。在一定的環(huán)境和控制條件下，用該點的發(fā)動機部件參數(shù)x和k帶入發(fā)動機穩(wěn)態(tài)模型進行仿真，所得發(fā)動機性能參數(shù)與該點發(fā)動機設計參數(shù)值相比較。

當發(fā)動機設計參數(shù)值被作為目標性能參數(shù)時，任何適當?shù)牟考拚齾?shù)和修正因子均可用代價函數(shù)來估計其模型修正能力的好壞，目標函數(shù)定義為。式(2)中，ai(i=1,2,…,6)和bj(j=1,2,…,m)是考慮不確定因素及目標性能參數(shù)的相對重要性權值。在此，假定所有目標性能參數(shù)的權重都相等，即：

式中：適應度函數(shù)在0～1之間變化，1表示最優(yōu)，0表示最差。

5 仿真結果與分析

5.1 修正前的穩(wěn)態(tài)模型計算結果

以發(fā)動機某狀態(tài)為例(設為工況1，Ma=0、H=0)，計算得到發(fā)動機模型修正前的目標性能參數(shù)，并與設計參數(shù)值進行比較分析，結果見表3。可見，修正前T5、T8、F與設計值偏差很大。如用此模型進一步分析發(fā)動機性能會產(chǎn)生較大誤差，因此有必要對發(fā)動機模型進行修正。

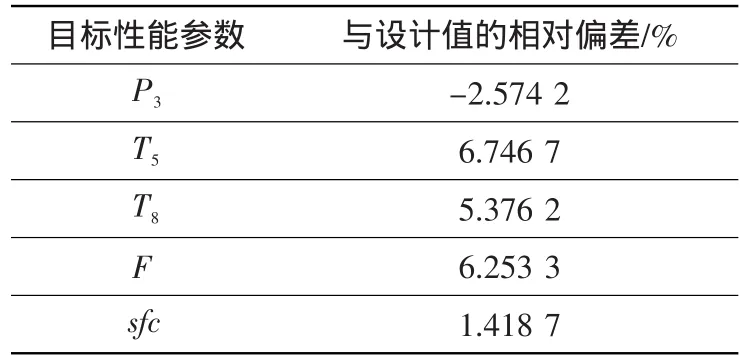
表3 模型修正前的目標性能參數(shù)偏差Table 3 Deviation of objective performance parameter before model modification

5.2 修正后的穩(wěn)態(tài)模型計算結果

采用前文的遺傳算法參數(shù)優(yōu)化流程修正發(fā)動機穩(wěn)態(tài)模型。經(jīng)反復試驗，最終確定交叉率為0.7，變異率為0.05，種群規(guī)模為40，在設計值附近隨機產(chǎn)生初始種群，最大迭代次數(shù)為100。修正后的結果見表4。對比表3和表4可知，經(jīng)遺傳算法修正后，發(fā)動機性能模型精度得到提高。

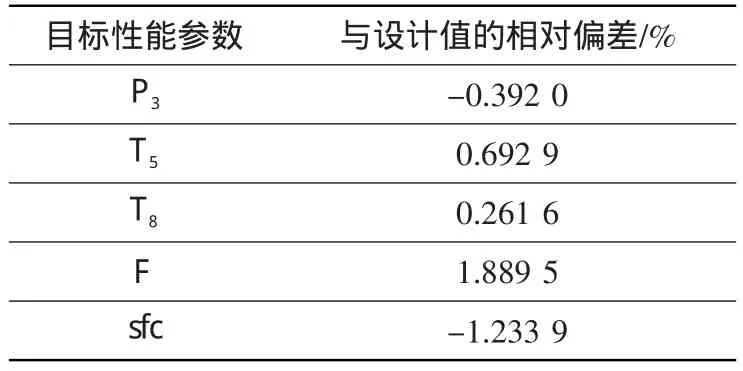
目標性能參數(shù)P3 T5 T8 F s f c與設計值的相對偏差/%-0.392 0 0.692 9 0.261 6 1.889 5-1.233 9

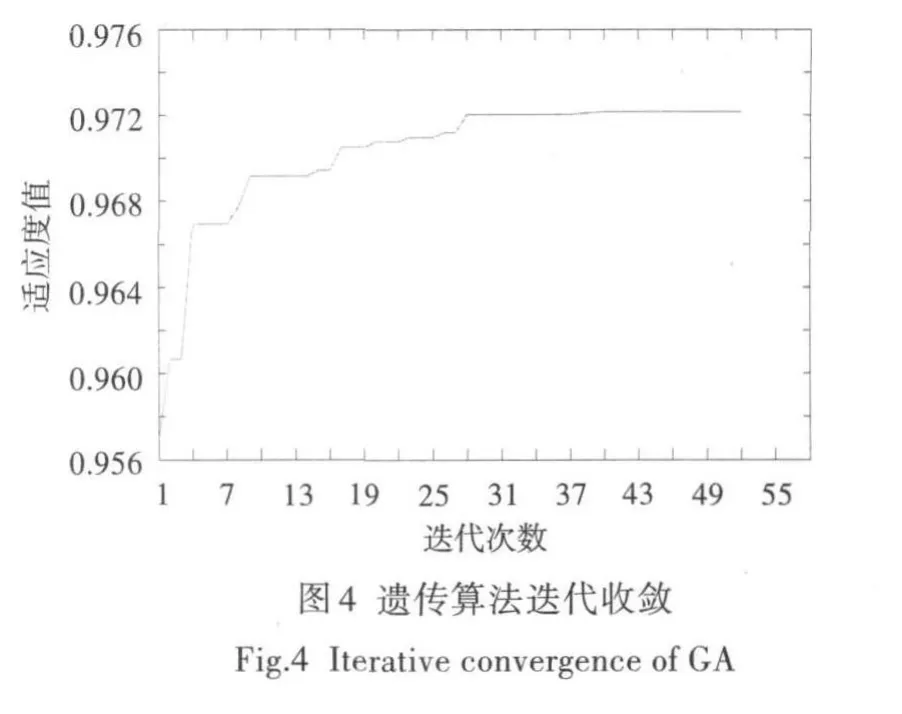
圖4示出了遺傳算法適應度值的變化過程。可見，經(jīng)過52次迭代，遺傳算法適應度值很快到達0.972，說明模型修正收斂速度較快。

5.3 與影響系數(shù)矩陣方法修正結果的對比

利用影響系數(shù)矩陣方法[4]對發(fā)動機穩(wěn)態(tài)模型進行修正。首先進行一次修正，得到一次修正矩陣：

一次修正后的目標性能參數(shù)偏差如表5所示。對比表3和表5可知，修正后T5、T8、F的精度提高，P3、sfc的精度降低。個別參數(shù)偏差仍然過大，有必要進行多次修正。

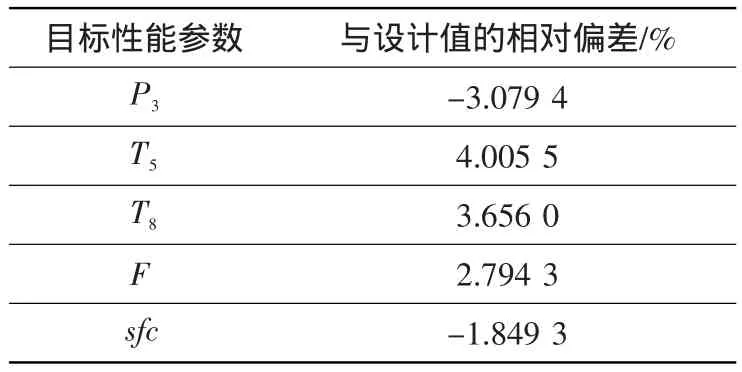
表5 一次修正后的目標性能參數(shù)偏差Table 5 Deviation of objective performance parameter after primary modification

進一步修正，得到多次修正矩陣為：

表6為經(jīng)多次修正后的目標性能參數(shù)偏差。對比表5和表6可知，多次修正后，目標性能參數(shù)與設計值的相對偏差減小，但精度低于遺傳算法修正結果。因此，單從精度方面講，遺傳算法修正精度優(yōu)于多次修正的影響系數(shù)矩陣方法。

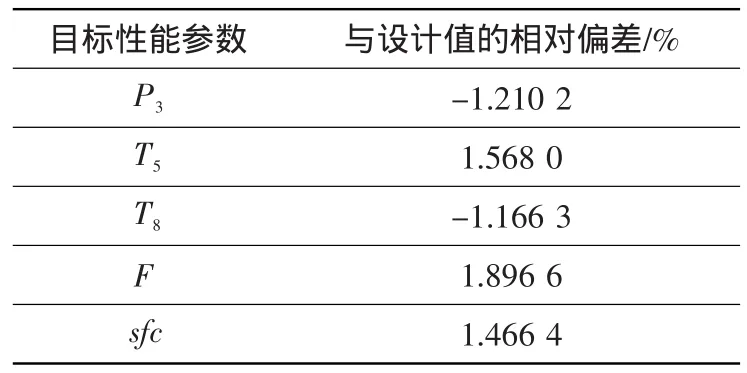
表6 多次修正后的目標性能參數(shù)偏差Table 6 Deviation of objective performance parameter after multiple modifications

5.4 不同部件修正參數(shù)組合的模型修正結果

基于遺傳算法，分別采用第二組和第三組部件修正參數(shù)進行修正。與設計值的相對偏差結果見表7。對比表7和表4發(fā)現(xiàn)，敏感程度最高的一組參數(shù)得到的模型修正效果最好。由此得到，正確選擇合適的修正參數(shù)，對模型修正效果起關鍵作用。

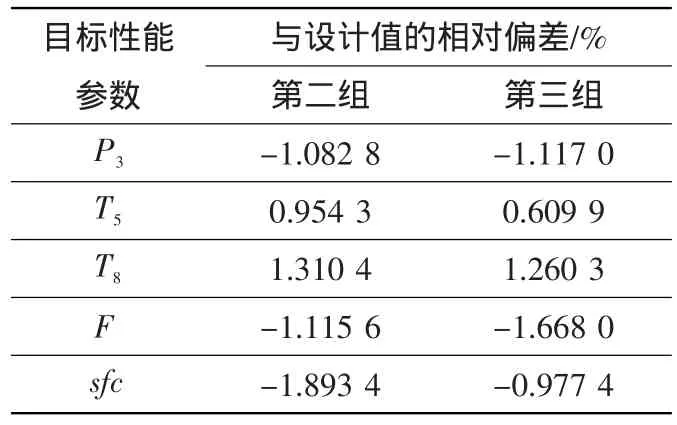
表7 不同部件修正參數(shù)組合的目標性能參數(shù)偏差Table 7 Deviation of objective performance parameter of various components

5.5 不同工況的模型修正結果

利用最敏感一組參數(shù)對發(fā)動機穩(wěn)態(tài)模型進行修正，另選取兩個工況(都為加力狀態(tài)，分別記為工況2和工況3)，驗證此組參數(shù)對模型修正的泛化能力。模型修正誤差結果如圖5所示。分析圖中可知，該組參數(shù)對模型修正具有較強的泛化能力，兩個工況的修正精度基本滿足要求。

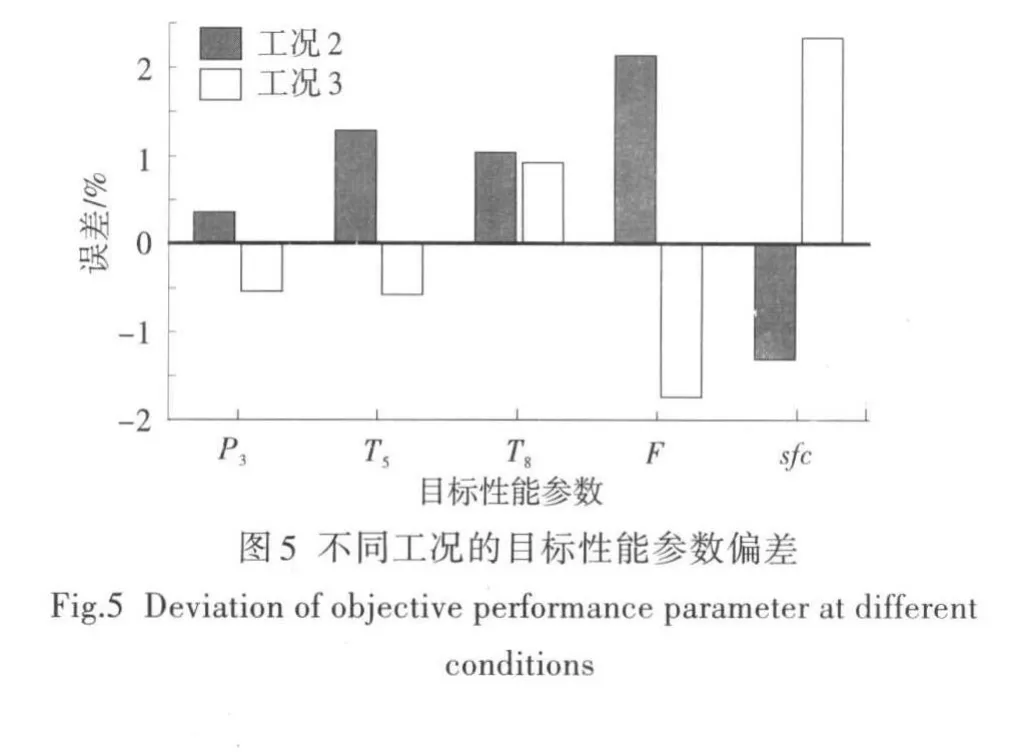
6 結論

(1)采用遺傳算法對發(fā)動機性能模型進行修正，其模型精度較修正前有很大提高，取得了不錯的修正效果。

(2)單從修正方面講，基于遺傳算法得到的修正效果比影響系數(shù)矩陣方法得到的修正效果更好。

(3)對不同部件修正參數(shù)組合的模型修正，選取的部件修正參數(shù)越敏感，模型修正的效果越好。

(4)利用相關性分析選取發(fā)動機部件修正參數(shù)修正不同工況的發(fā)動機性能模型，可取得較好效果。

[1]翟高蘭.航空發(fā)動機非線性參數(shù)估計方法[D].南京：南京航空航天大學，2008.

[2]蘇三買.遺傳算法及其在航空發(fā)動機非線性數(shù)學模型中的應用研究[D].西安：西北工業(yè)大學，2002.

[3]尹大偉.航空發(fā)動機模型求解算法及性能尋優(yōu)控制中的參數(shù)估計研究[D].長沙：國防科技大學，2011.

[4]Escher P C，Singh R.An Objective-Oriented Diagnostics Computer Program Suitable for Industrial Gas Turbine[C]//.21stInternational Congress on Combustion Engines.Switzerland，1995.

[5]尹大偉，李本威.某型渦扇發(fā)動機模型修正研究[C]//.中國航空學會第六屆動力年會.2006.

[6]李本威，尹大偉，王永華，等.某型渦扇發(fā)動機狀態(tài)模型修正[J].海軍航空工程學院學報，2008，23(2)：213—216.

[7]付堯明，傅 強.非線性航空發(fā)動機性能參數(shù)估計方法研究[J].機械設計與制造，2006，(8)：140—141.

[8]Mathioudakis K，Kamboukos Ph，Stamatis A.Turbofan Performance Deterioration Tracking Using Nonlinear Models and Optimization Technique[J].Journal of Turbomachinery，2002，124(10)：580—587.

[9]謝小平.基于單機修正的某型發(fā)動機氣路模型的建立研究[D].山東煙臺：海軍航空工程學院，2011.