二級旋轉倒立擺的逐級模糊實時控制

高 強， 李 毅， 陳莎莎

（1.天津理工大學 自動化學院 天津市復雜控制理論與應用重點實驗室，天津 300384；2.南開大學 信息技術科學學院，天津 300071）

二級旋轉倒立擺的逐級模糊實時控制

高 強1， 李 毅2， 陳莎莎1

（1.天津理工大學 自動化學院 天津市復雜控制理論與應用重點實驗室，天津 300384；2.南開大學 信息技術科學學院，天津 300071）

文章根據柯尼希定理，應用拉格朗日方程，建立了二級旋轉倒立擺系統的動力學方程，并計算出系統一般形式的狀態方程組；應用基于T－S模糊模型，設計了按照上擺桿、下擺桿和旋轉臂分級優先順序的逐級模糊控制器，實現了對旋轉倒立擺系統的實時控制。控制結果表明，逐級模糊控制可滿足實時控制要求，具有控制精度高、穩定性好的特點。

二級旋轉倒立擺；T－S模型；逐級建模控制；柯尼希定理

倒立擺系統的控制問題是控制領域的經典問題。倒立擺系統的研究始于20世紀50年代，由于其具有高階次、多變量、非線性、強耦合和不穩定的特性，研究人員一直將它視為典型的研究對象，并不斷從中探索新的控制理論和控制方法。雖然我國對倒立擺的研究起步比較晚，但是值得一提的是，2010年6月18日，李洪興教授的課題組在世界上首次實現了空間四級倒立擺實物控制。

本文提出使用柯尼希定理對擺桿能量進行分析計算，相比于傳統方法［1］，大大減少了計算量，進而可以推導出精確的二級旋轉倒立擺的數學模型；根據模型設計控制器，采用所設計的逐級模糊控制器實時控制二級旋轉倒立擺系統。實時控制的難度在于，在控制過程中會出現許多控制干擾因素，同時，控制算法還需要滿足控制的實時性要求。實時控制環境能更加接近復雜的、惡劣的現場環境，更能驗證算法的實際可行性，這是仿真中不能體現的。因此，實時控制倒立擺在對控制算法的實踐檢驗上，具有重要的意義。

1 二級旋轉倒立擺系統研究

基于動力學分析，建立旋轉倒立擺系統數學模型，這是實現倒立擺控制的基礎。旋轉倒立擺的模型結構如圖1所示。忽略各種摩擦力和阻力，旋轉臂、下擺桿和上擺桿可以抽象為均勻質桿，編碼器抽象為質點，其中旋臂長度為R，其與OXYZ坐標系中的Y軸的夾角為α；下擺桿的質量為m1，長度為L1，其與O1X1Y1Z1坐標系中的Z1軸的夾角為β，質心位置為擺桿的中點；上擺桿的質量為m2，長度為L2，其與O2X2Y2Z2坐標系中的Z2軸夾角為θ，質心位置為擺桿的中點；編碼器的質量為mE，所在位置為下擺桿與上擺桿連接處（圖1中O2處）。相應地，˙α為旋臂角速度，為下擺桿角速度為上擺桿角速度。Jeq為旋轉臂的轉動慣量。旋轉臂在平面XOY內運行，下擺桿在平面X1O1Z1內運行，上擺桿在平面X2O2Z2內運行。

圖1 二級旋轉倒立擺系統結構示意圖

1.1 旋轉臂的動能和勢能

動能為Ek旋臂＝（Jeq）／2，勢能以旋臂所在平面為零勢能面，即Ep旋臂＝0。

1.2 下擺桿的動能和勢能

根據柯尼希定理可知下擺桿的動能為：

利用坐標系之間的齊次變換矩陣［2］（1）式，可寫出下擺桿質心在OXYZ坐標系中的坐標表示，即（2）式。設動坐標系o－uvw初始位置與定坐標系OXYZ重合，相對于動坐標系o－uvw進行變換，根據右手定則以及對α角的定義，o－uvw→O1X1Y1Z1可以看做是動坐標系o－uvw先平移到點［Rsinα，Rcosα，0］，再對w軸旋轉（－α）的疊加，即

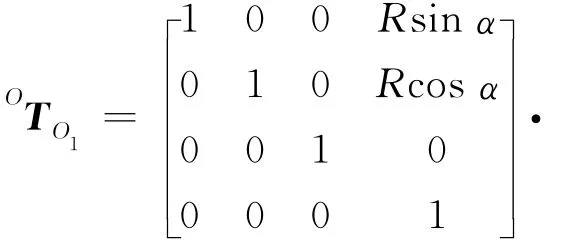
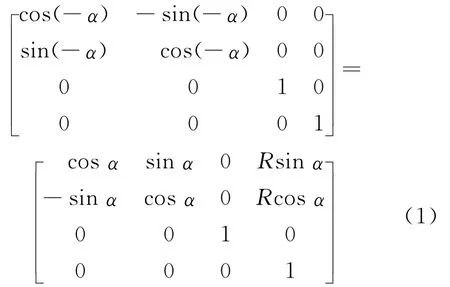
于是有：

整理可以得到速度表達式為：

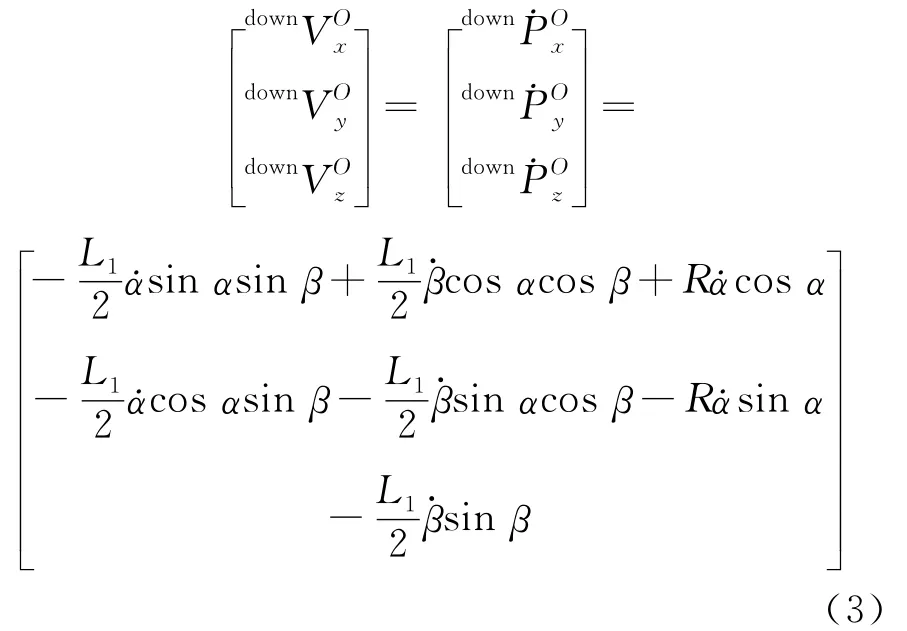
由于：

下擺桿相對其質心的轉動動能為：

下擺桿的勢能為：

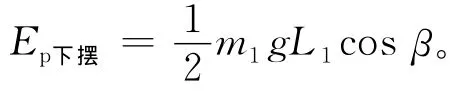
1.3 編碼器的動能和勢能

由于：

可以得知編碼器的速度為：

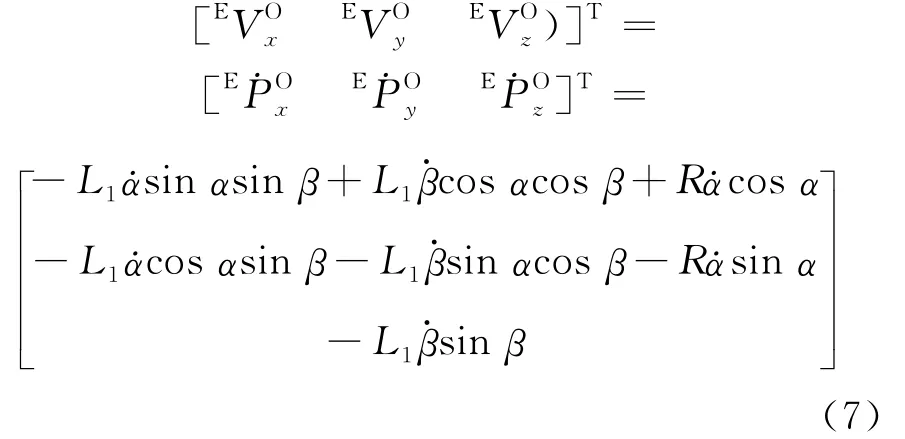
編碼器的動能為：

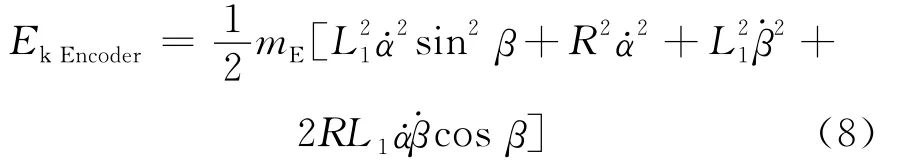
編碼器的勢能為：

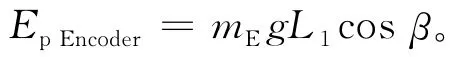
1.4 上擺桿的動能和勢能

根據柯尼希定理可知上擺桿的動能為：

利用坐標系之間的齊次變換矩陣（9）式，可寫出上擺桿質心在OXYZ坐標系中的坐標表示，即（10）式。o－uvw→O1X1Y1Z1→O2X2Y2Z2相對于動坐標系o－uvw進行變換，可以看做是在O的基礎上，再平移到點［L1sinβ，0，L1cosβ］。

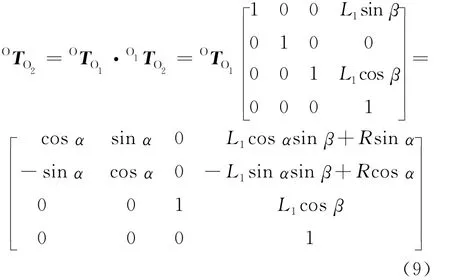
于是有：

整理可以得到速度表達式：

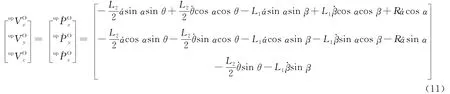
所以：

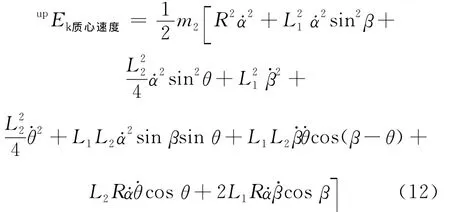
上擺桿相對其質心的轉動動能為：

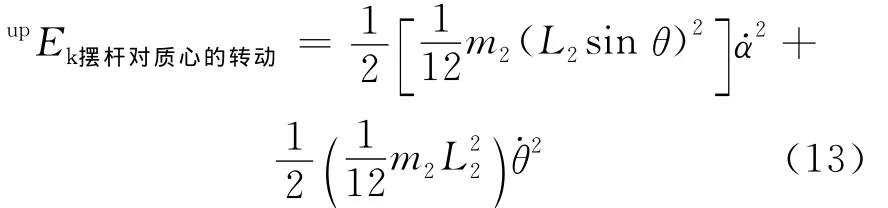
上擺桿的勢能為：

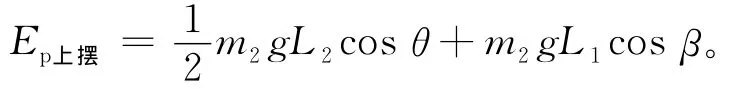
1.5 Lagrange方程

Lagrange函數為：

忽略各種摩擦力和阻力，所以二級旋轉倒立擺的Lagrange方程為：

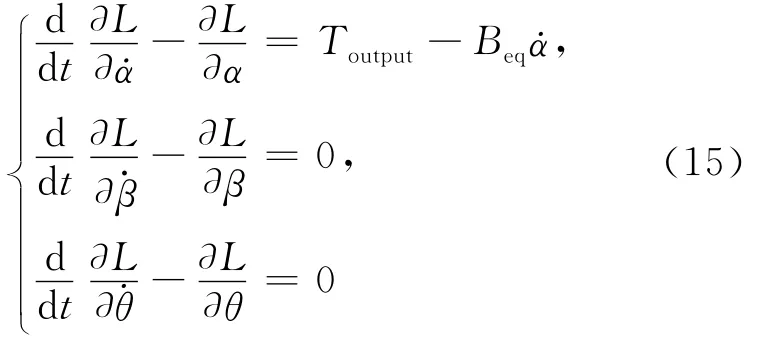
進而可以得到系統的數學模型：

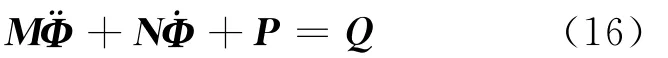
其中

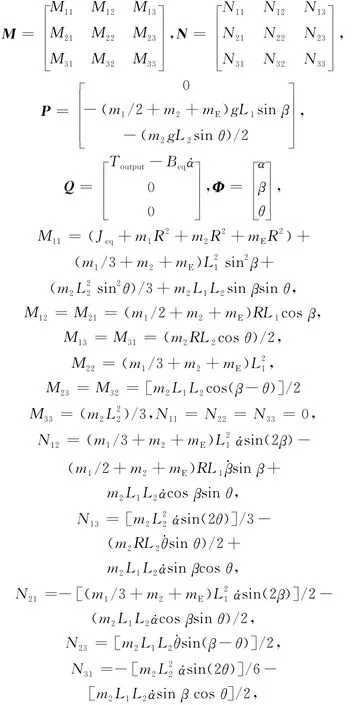
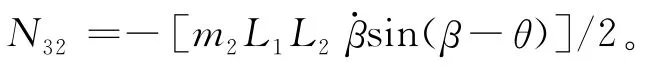
本文推導的數學模型應用柯尼希定理，可以使研究者對倒立擺的物理特性更加明了清晰。

2 基于T－S模型的逐級模糊控制

通過對實時控制實驗的觀察，系統各部分穩定的重要性分級為上擺桿為高級，下擺桿為中級，旋轉臂為低級。按照分級優先順序，設計基于TS 模糊模型［3－4］的逐級模糊控制器［4－5］。

逐級控制采用全局狀態變量作為模糊控制器［6－7］的輸入。論域設定為：theta∈［－8／180＊pi，＋8／180＊pi］，beta∈［－12／180＊pi，＋12／180＊pi］，alpha∈［－0.3，＋0.3］；theta－dot∈［－1，＋1］，beta－dot∈［－1，＋1］，alpha－dot∈［－2，＋2］。theta變量用3個模糊子集｛－8 0 8｝來描述，beta變量用3個模糊子集｛－12 0 12｝來描述，均采用高斯型，全交疊、均勻分布隸屬度函數。theta－dot變量用3個模糊子集｛－1 0 1｝來描述，beta－dot變量用3個模糊子集｛－1 0 1｝來描述，alpha變量用3個模糊子集｛－0.3 0 0.3｝來描述，alpha－dot變量用3個模糊子集｛－2 0 2｝來描述，均采用高斯型，全交疊、均勻分布隸屬度函數。

按照分級控制的思想，對（16）式進行局部線性化，可求得如下的模糊模型。

（1）若theta是8°，theta－dot是1，或theta是－8°，theta－dot是－1，則˙x＝A1x＋B1u。

（2）若theta是8°，theta－dot是－1，或theta是－8°，theta－dot是1，則˙x＝A2x＋B2u。

（3）若theta是8°，theta－dot是0，或theta是－8°，theta－dot是0，則˙x＝A3x＋B3u。

（4）若theta是0°，theta－dot是1，或theta是0°，theta－dot是－1，則˙x＝A4x＋B4u。

（5）若theta 是 0°，theta－dot是 0，beta 是－12°，beta－dot是－1，或theta是0°，theta－dot是0，beta是12°，beta－dot是1，則˙x＝A5x＋B5u。

（6）若theta 是 0°，theta－dot是 0，beta 是－12°，beta－dot是 1，或theta是 0°，theta－dot是0，beta是12°，beta－dot是－1，則˙x＝A6x＋B6u。

（7）若theta 是 0°，theta－dot是 0，beta 是－12°，beta－dot是 0，或theta是 0°，theta－dot是0，beta是12°，beta－dot是0，則˙x＝A7x＋B7u。

（8）若theta是 0°，theta－dot是 0，beta是0°，beta－dot是－1，或theta是0°，theta－dot是0，beta是0°，beta－dot是1，則˙x＝A8x＋B8u。

（9）若theta是 0°，theta－dot是 0，beta是0°，beta－dot是0，alpha是 ｛－0.3°，0°，0.3°｝中的任意一個，alpha－dot是 ｛－2，0，2｝中的任意一個，則＝A9x＋B9u。

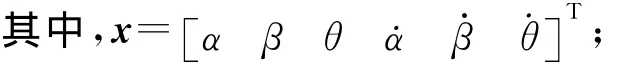
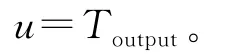
考慮對每一個線性子系統設計一個局部的線性狀態反饋控制器。對每個局部模型的期望閉環極點都選為：－96.677 9，－9.430 7＋3.373 4i，－9.430 7－3.373 4i，－4.276 6＋1.572 5i，－4.276 6－1.572 5i，－1.002 2。可以求得對應每個子系統的局部反饋增益矩陣為：

輸出變量Toutput用9個模糊子集｛1 2 3 4 5 6 7 8 9｝來描述。其中，具體控制規則見表1所列。

表1 逐級模糊控制規則表

模糊規則L1～L25的后件如下所示：

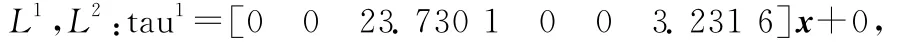
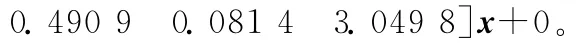
其中，tau1～tau9即為輸出變量Toutput對應的9個級別。解模糊采用加權平均法（weighted average）。

該實時控制的實驗是基于加拿大Quanser公司的SRV－02旋轉倒立擺平臺，實時控制系統為Quarc，可以與Simulink無縫編譯連接，如圖2所示。在圖2中，“T－S every”為基于 T－S模型的逐級模糊控制模塊。取穩定控制過程中的20s數據，實時控制結果如圖3所示。

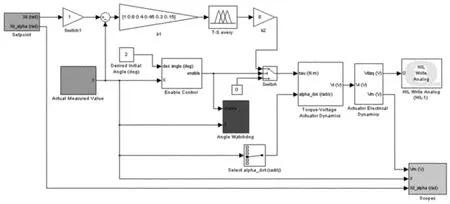
圖2 基于T－S模型逐級模糊控制的實時控制結構圖

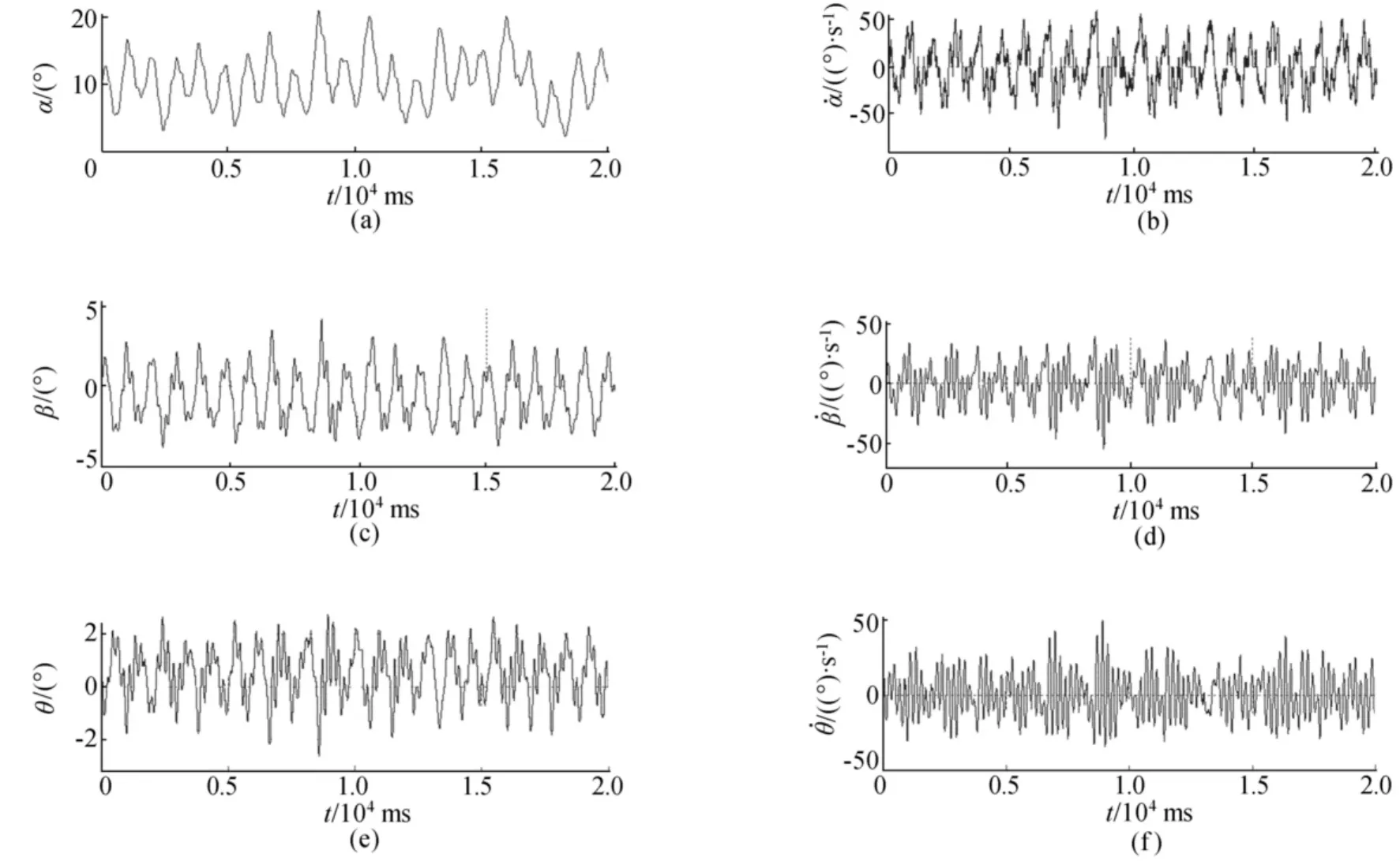
圖3 基于T－S模型逐級模糊控制的實時控制結果

實時控制結果表明，基于T－S模型的逐級模糊控制可使二級旋轉倒立擺系統“倒立”。控制器在使倒立擺穩定的情況下，使角alpha在設定值10°附近運動，基本控制在［5°，15°］，使角beta基本控制在［－3°，＋3°］，使角theta基本控制在［－2°，＋2°］，以及使alpha－dot、beta－dot和theta－dot均在可控制范圍內，因此基于T－S模型的逐級模糊控制器完全滿足設計要求。角theta的控制精度得到了明顯提高，其運行區間更加對稱，表明了系統更加穩定，充分說明了逐級控制方法的正確性、優異性。

3 結束語

本文詳細推導了二級旋轉倒立擺的數學模型，提出使用柯尼希定理解決擺桿能量的問題，使得建模過程中的計算量減少，避免了大計算量帶來的實時控制實現困難，提高了建模的精度，實現了基于T－S模型的逐級模糊控制器，克服了實時控制中的各種不確定的干擾，提高了控制精度，也增強了控制的穩定性。該算法還可進一步使用遺傳算法、粒子群算法、蟻群算法等，尋找最優閉環極點，進而設計出控制精度更高的控制器。

［1］但遠宏，賴紅霞.環形二級倒立擺的建模與能觀性和能控性分析［J］.重慶工學院學報：自然科學版，2007，21（11）：7－16.

［2］韓建海.工業機器人［M］.武漢：華中科技大學出版社，2009，50－56.

［3］Shi Xiaoxia，Zhong Qiuhai.The mathematic model for the double inverted pendulum based on state feedback and T－S model［C］／／SICE Annual Conference，2003：1457－1460.

［4］陳澤望.二級倒立擺系統的模糊控制研究［D］.沈陽：東北大學，2008.

［5］朱學峰，周文彬，陳華艷.二級倒立擺的T－S型逐級模糊神經網絡控制［J］.華南理工大學學報：自然科學版，2005，33（2）：43－47.

［6］諸 靜.模糊控制理論與系統原理［M］.北京：機械工業出版社，2005，393－399.

［7］Zadeh L A.Fuzzy sets［J］.Information and Control，1965，8：338－353.

Real－time control of rotary double inverted pendulum system by using gradual fuzzy algorithm

GAO Qiang1， LI Yi2， CHEN Sha－sha1
（1.Tianjin Key Laboratory for Control Theory and Applications in Complicated System，School of Automation，Tianjin University of Technology，Tianjin 300384，China；2.School of Information Technical Science，Nankai University，Tianjin 300071，China）

The dynamics equation of a rotary double inverted pendulum system is deduced by applying Konig theorem and Lagrange method，and the state equation set of the system in general form is calculated.A gradual fuzzy controller is designed by means of the T－S fuzzy model.For the real－time control of the system，the upper pendulum has a high priority，the lower pendulum has a middle priority and the rotary arm has a low priority.The results of the real－time experiment prove that the gradual fuzzy algorithm based on T－S model can satisfy the requirement of real－time control and has better control precision and stability.

rotary double inverted pendulum；T－S model；gradual fuzzy control；Konig theorem

TP20

A

1003－5060（2012）11－1474－07

10.3969／j.issn.1003－5060.2012.11.009

2012－04－27；

2012－06－30

高 強（1962－），男，天津市人，天津理工大學教授，碩士生導師.

（責任編輯 張 镅）