基于半平面上的不重疊Schwarz交替法

劉紅梅， 王壽城

（合肥工業大學 數學學院，安徽 合肥 230009）

基于半平面上的不重疊Schwarz交替法

劉紅梅， 王壽城

（合肥工業大學 數學學院，安徽 合肥 230009）

文章討論了基于半平面上自然邊界歸化的無界區域上不重疊Schwarz交替法及其離散化，對于區域的分解方法是將無界的半平面分解為不重疊的2個區域，即很小的有界區域和無界的半平面，并且在有界區域和無界區域上分別交替利用有限元法和自然邊界元法求解，對于其中離散情形的不重疊型區域，分解算法利用極值原理證明其在最大模意義下的幾何收斂性。

不重疊Schwarz交替法；半平面；自然邊界元；離散化；極值原理；幾何收斂

0 引 言

文獻［1－4］給出了有界區域的不重疊Schwarz交替法，基于自然邊界歸化處理無界區域問題的理論，本文將不重疊Schwarz交替法推廣到無界區域上，即將無界半平面Ω分解為一個很小的有界區域Ω1和一個無界區域Ω2，在Ω1上可用標準有限元方程，而在Ω2上則可直接通過自然邊界歸化得到的Poisson積分公式。

本文考慮Possion方程的外邊界問題，即

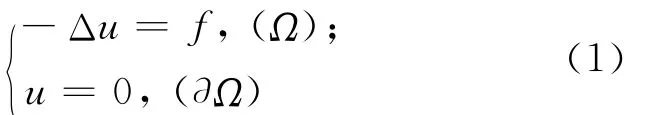
其中，Ω為適當光滑的曲線Γ0下方的無界區域，Γ0＝Γ01∪Γ02，Γ01為在上半平面中的簡單開曲線段，且的左右端點A和B在x軸上，Γ02＝｛（x，y）｜y＝0｝／，如圖1所示。

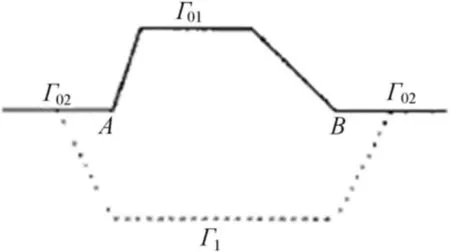
圖1 無界區域及其分解Ω＝Ω1∪Ω2

對于問題（1），本文給出連續情形的不重疊Schwarz算法和離散情形的不重疊Schwarz算法，并在線性元的情況下利用離散極值原理證明離散情形的幾何收斂性。

1 算法及其離散化

不妨在Γ01下方作簡單曲線Γ1，使得Γ0和Γ1所圍的區域Ω1的邊界?Ω1適當光滑，記下半平面為Ω2，Γ2＝?Ω1／Γ1。

對應（1）式的弱形式是求u∈H1（Ω），滿足

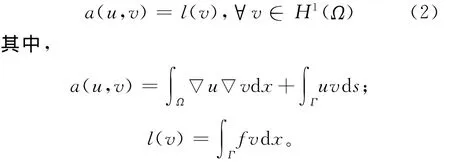
本文采用

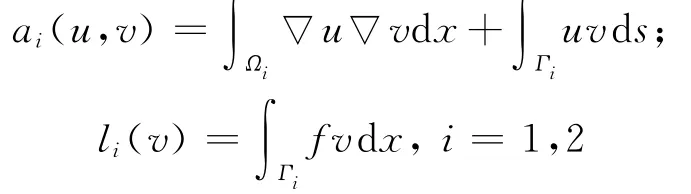
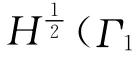
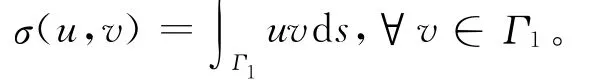
下面構造（1）式的解的迭代過程。

算法1 不重疊Schwarz交替法。其迭代步驟為：

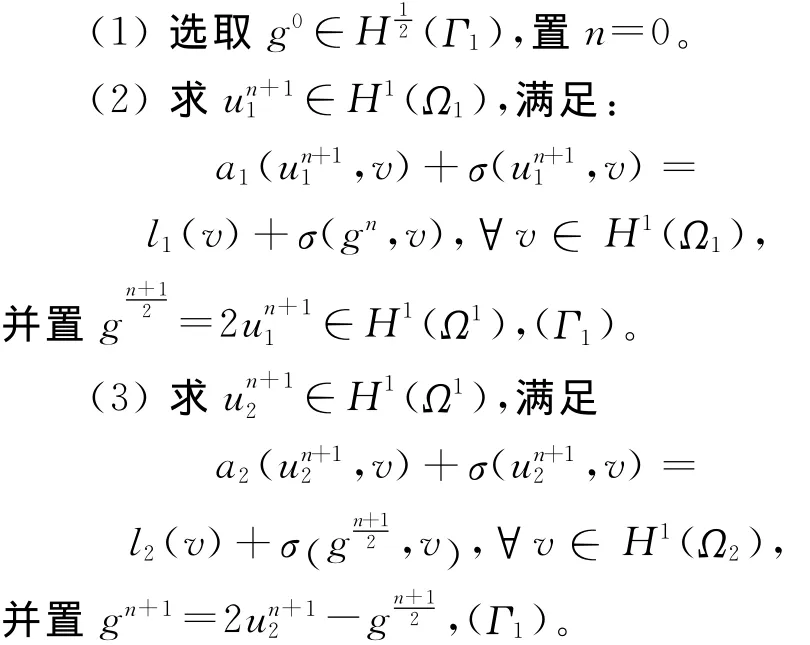
（4）置n＝n＋1，轉步驟（2）。

算法1的有限元模擬為：首先對Ω1作正則三角形剖分（或四邊形剖分），Pi（i＝1，2，…，N）為內結點，Pi（i＝N＋1，N＋2，…，N＋M）為邊界結點，即Ω1h上的線性元空間為Sh（Ω1h），用Γ1h表示剖分在Γ1上的分劃，Γ2h表示剖分在Γ2上的分劃，Φh表示Sh（Ω1h）在Γ1上的跡空間［5－6］。

（1）式的有限元近似為求uh∈Sh（Ω1h），滿足a（uh，v）＝l（v），?v∈Sh（Ω1h）。

下面對算法1進行離散模擬。

算法2 離散不重疊Schwarz交替法。其迭代步驟為：

（1）選取初始g0∈Φh，置n＝0。

（2）求∈Sh（Ω1h），滿足：

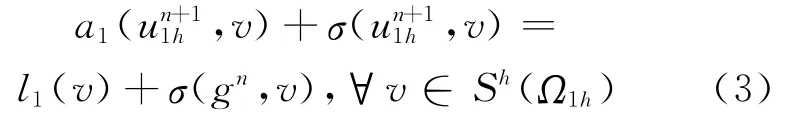
并置

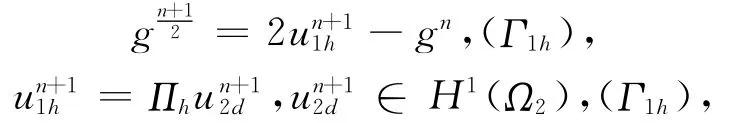
其中，Πh：C（Γ1）→Sh（Ω1h）上的插值算子。

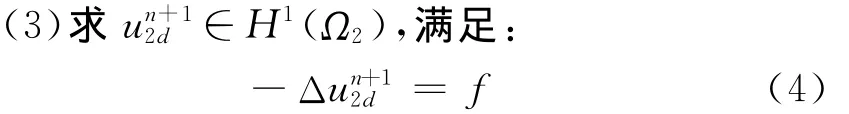
（4）轉步驟（2）。

對于離散的不重疊Schwarz算法中的（3）式在Sh（Ω1h）上利用有限元求解，（4）式在下半平面利用Poisson積分公式求解［7］，即

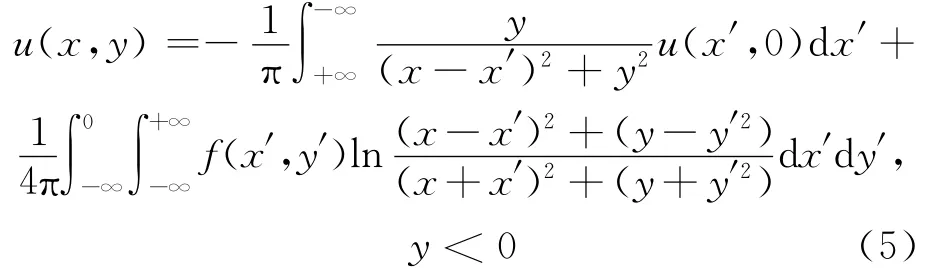
2 離散情形的幾何收斂性

從而離散強極值原理成立［8－9］。

引理1 設ωh∈Sh（Ω1h），且滿足：

若令q0h＝sup｛ωh（x，y）｜（x，y）∈Ω1h｝，則0＜q0h＜1。

定理1 由（3）式和（4）式給定的序列｛｝和｛｝分別在Ω1h和Ω2上幾何收斂，若分別設收斂解為uh和ud，則

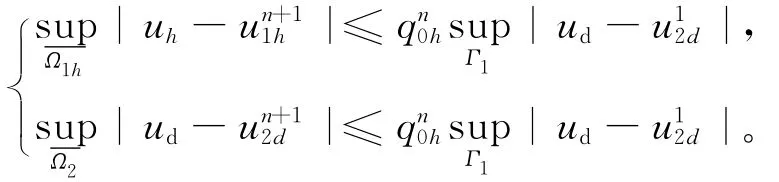
由（3）式和（4）式可得：

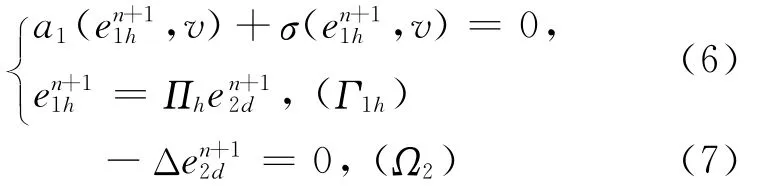
由（6）式和引理1得：

利用離散極值原理可得：

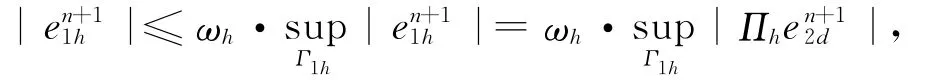
在Ω1h內，由引理1得：

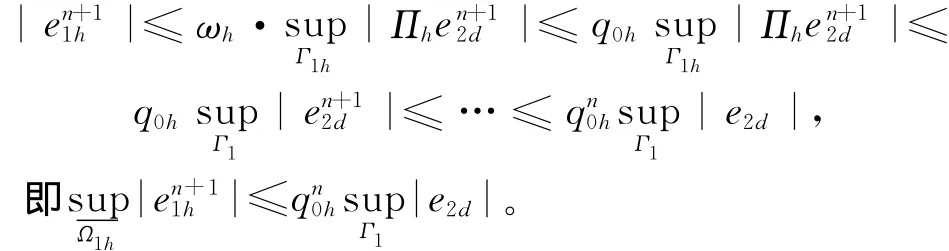
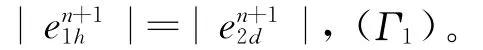
2d｜，定理1得證。

對于算法1的收斂性，可以通過算法2的收斂性及h→0的極限過程得到。

3 結束語

本文證明了無界區域的Schwarz迭代是幾何收斂的，且離散情形的算法在有界區域和無界區域是不對稱的，在有界區域上可用標準有限元方程求解，而在無界區域上則可直接應用Poisson積分公式直接求解。

［1］呂 濤，石濟民，林振寶.區域分解算法：偏微分方程數值解新技術［M］.北京：科學出版社，1992：227－231.

［2］余德浩.無界區域上基于自然邊界歸化的區域分解算法［J］.計算數學，1994，16（4）：448－459.

［3］余德浩.無界區域非重疊區域分解算法的離散化及其收斂性［J］.計算數學，1996，18（3）：328－336.

［4］蔣美群，鄧慶平.一個雙調和方程的Schwarz交替法［J］.計算數學，1994，16（1）：93－101.

［5］余德浩.自然邊界元方法的數學理論［M］.北京：科學出版社，1993：71－103.

［6］數學手冊編寫組.數學手冊［M］.北京：高等教育出版社，1979：559－593.

［7］鄭 權.余德浩.基于半平面上自然邊界歸化的無界區域上的Schwarz交替法及其離散化［J］.計算數學，1997，19（2）：205－218.

［8］Ciarlet P G，Raviart P A.Maximum principle and uniform convergence for the finite element method［J］.Comput Methods Appl Mech Engrg，1973，2：17－31.

［9］Wang Leiheng.On the max－min principle for the linear finite element equation for the Dirichlet problem of Laplace equation［C］／／Proc of China－France Symp on FEM.Beijing：Science Press，1983：1019－1026.

An underlapping Schwarz alternating method over half－plane

LIU Hong－mei， WANG Shou－cheng
（School of Mathematics，Hefei University of Technology，Hefei 230009，China）

In this paper，an underlapping Schwarz alternating method of unbounded domains based on natural boundary reduction over half－plane and its discretization are discussed.The unbounded halfplane is decomposed into two underlapping domains，namely a bounded domain and an unbounded domain，and the finite element method and natural boundary element method are used in these two domains respectively for their solutions.And the geometric convergence of the underlapping Schwarz alternating method in discrete problem under the maximum module is shown by the extremum principle.

underlapping Schwarz alternating method；half－plane；natural boundary element；discretization；extremum principle；geometric convergence

O241.82

A

1003－5060（2012）11－1582－03

10.3969／j.issn.1003－5060.2012.11.033

2012－03－16

劉紅梅（1987－），女，安徽六安人，合肥工業大學碩士生；

王壽城（1956－），男，安徽壽縣人，合肥工業大學副教授，碩士生導師.

（責任編輯 閆杏麗）