半剛性預壓裝配式PC框架彎矩調幅系數的研究

黃慎江， 屈克達， 張克勤， 柳炳康

（合肥工業大學 土木與水利工程學院，安徽 合肥 230009）

半剛性預壓裝配式PC框架彎矩調幅系數的研究

黃慎江， 屈克達， 張克勤， 柳炳康

（合肥工業大學 土木與水利工程學院，安徽 合肥 230009）

文章結合一榀單層2跨預壓裝配式PC框架實驗，考慮節點半剛性的影響，分析了預壓裝配式預應力混凝土框架延性系數的影響因素，導出預壓裝配式PC框架梁端截面屈服曲率表達式和極限曲率表達式，計算了梁端截面延性系數并與試驗值進行比較；導出了預壓裝配式PC框架梁端滿足承載力要求和使用要求的截面延性系數和彎矩調幅限值，考慮節點半剛性的影響和裂縫寬度限值的要求，給出了彎矩調幅限值建議公式以及彎矩調幅系數限值，為預壓裝配式框架的設計提供了理論基礎。

預壓裝配式框架；半剛性節點；彎矩調幅

預壓裝配式預應力混凝土結構是后張有黏結裝配式預應力混凝土結構，它通過預制構件接合部穿連并張拉預應力筋的連接方式，將后張預應力筋穿過梁、柱預留孔道，最后實施預應力張拉預壓，使之形成受力整體。后張預應力筋既可以作為施工時的拼裝手段，又可以在使用階段承受梁端彎矩，構成連續受力的整體框架。由于在拼裝節點處僅有預應力筋連接，節點具有半剛性特征，因此，應對彈性方法計算的框架彎矩值考慮塑性內力重分布進行適當調整。

普通鋼筋混凝土超靜定結構采用彎矩調幅法考慮塑性內力重分布的研究已比較成熟，一些學者也對預應力混凝土結構塑性內力重分布進行了相關的研究，對于預壓裝配式預應力混凝土結構彎矩調幅系數的研究很少。本文在試驗的基礎上，考慮節點半剛性的影響，分析了影響預壓裝配式PC框架內力重分布的因素，導出結構在滿足承載力要求和正常使用要求下的彎矩調幅系數公式，為預壓裝配式框架的設計提供了理論基礎。

1 影響梁端截面延性的因素

預壓裝配式結構具有良好的延性性能，試驗表明：在梁端截面延性系數達到4時，承載力并無明顯降低，且具有良好的變形恢復能力［1］。

1.1 截面延性

框架結構的梁端延性可用截面延性度量，預壓裝配式框架梁端截面預應力筋開始屈服時和達到截面最大承載力時的截面應變分布分別如圖1、圖2所示。由截面應變分布符合平截面假定，可導出梁端截面屈服曲率表達式和極限曲率表達式如下。

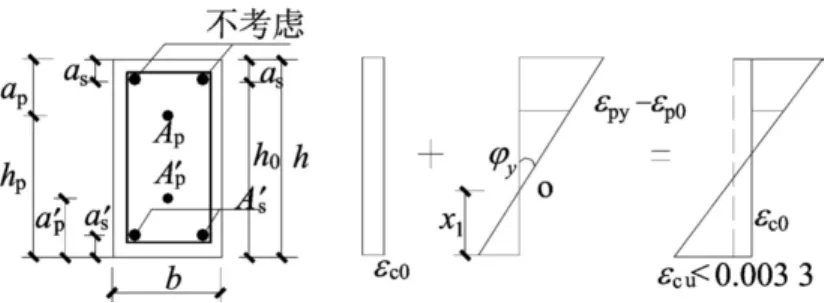
圖1 框架梁端屈服應變圖

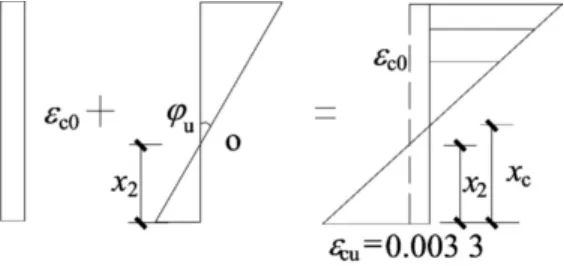
圖2 框架梁端極限應變圖

梁端截面的屈服曲率：

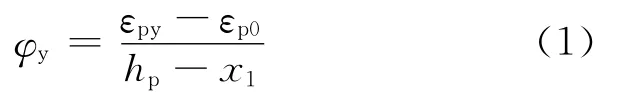
梁端截面的極限曲率：

梁端截面極限受壓區高度：

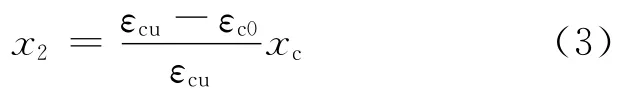
根據文獻［1］的實驗結果，梁端截面屈服受壓區高度與極限受壓區高度之比x1／x2≈1.34～1.40，近似取x1＝1.37x2；梁端截面受壓區高度x與平截面假定得中和軸高度xc的比值取為x＝0.8xc。因此，預壓裝配式PC框架梁端截面曲率延性可表示為：

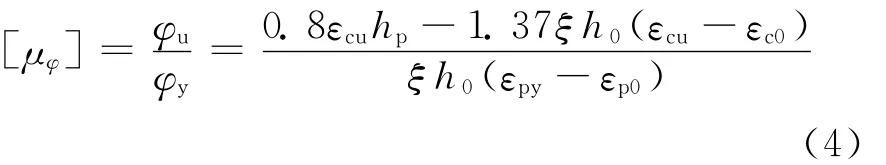
其中，εc0為預應力鋼筋張拉完成后混凝土的初始線應變。對于截面對稱配置預應力筋且張拉控制應力相同的預壓裝配式構件截面應力、應變分布如圖3所示。εc0可由截面平衡條件按（5）式進行計算。

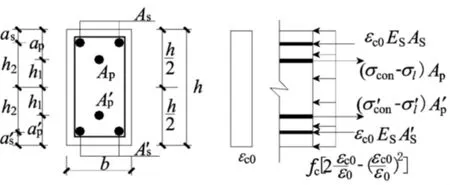
圖3 框架梁張拉完成后梁端截面的應力、應變圖

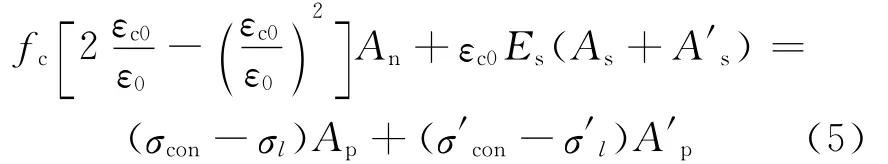
整理可得：

根據文獻［1］中KJ－1的實驗結果，實測延性系數和用（4）式計算結果的比較見表1所列，可以看出計算值和實驗值吻合較好。

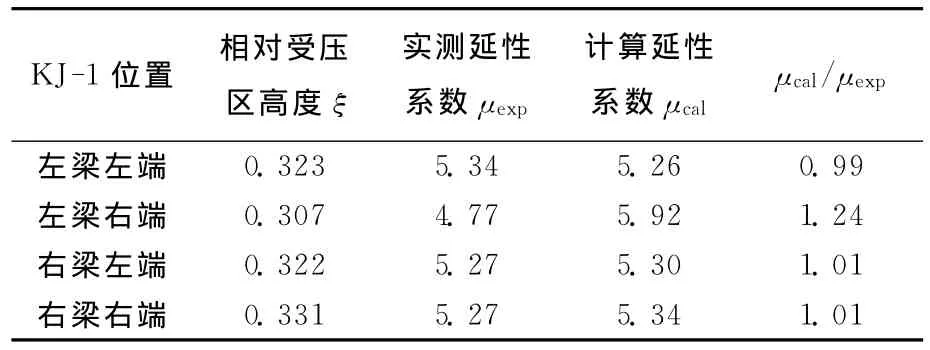
表1 梁端截面延性系數計算值與實測值的比較

1.2 梁端截面延性影響因素

根據（4）式，可以看出影響預壓裝配式PC框架梁端截面延性系數的因素主要有：

（1）混凝土極限壓應變εcu。在預應力鋼筋型號、相對受壓區高度ξ和初始壓應變εc0確定的情況下，截面延性系數隨著壓應變的增大而增大。對于預壓裝配式框架，由于牛腿截面和梁端缺口處均配置了構造鋼筋，使得受壓區極限壓應變εcu達常規值的2倍左右才出現破壞［2］，因此，預壓裝配式結構具有較好的截面延性。

（2）截面相對受壓區高度ξ。在其他參數固定的情況下，截面相對受壓區高度ξ越大，延性系數越差。在進行彎矩調幅時要控制截面的相對受壓區高度ξ不要超過某一限值。

（3）預應力鋼筋型號。根據（4）式可以看出，梁端截面延性的大小與預應力鋼筋的屈服應變εpy和初始拉應變εp0的差值有關。

2 滿足承載力要求的彎矩調幅限值

2.1 滿足承載力要求的截面延性

在節點半剛性的影響下，梁端彎矩會自動調幅到跨中。以單層2＃跨預壓裝配式PC框架為例，考慮節點半剛性影響下框架的內力計算可以根據文獻［3］中推導的單元剛度矩陣，采用矩陣位移法求得。假設節點相對轉動剛度K相同，柱高為H，梁跨長為L，梁柱線剛度之比為α＝ib／ic，結構承受跨中集中荷載P，現對中支座彎矩調幅β′。假設結構滿足在中間支座破壞前其他梁端柱端均不屈服，當荷載增加至（1－β′）P時，中支座截面延性能夠滿足彎矩調幅的要求。塑性轉角分析如圖4所示。

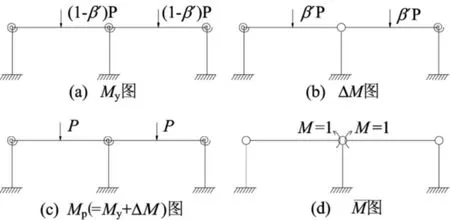
圖4 塑性轉角分析圖

根據虛功原理，中支座的塑性轉角θp可表示為：

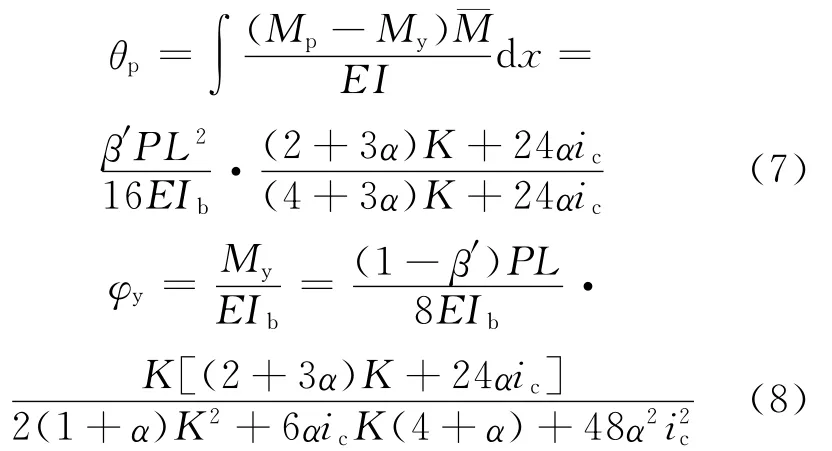
根據預壓裝配式預應力混凝土框架實驗的統計結果，塑性鉸的長度可近似取lp＝0.5h0。塑性轉角公式可表示為：

令ψc＝ic／K，ψc為柱線剛度ic與節點相對轉動剛度K之比。將（7）式、（8）式代入（10）式，則可得滿足承載力要求的梁端截面延性：

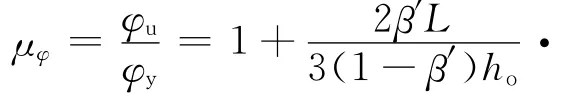
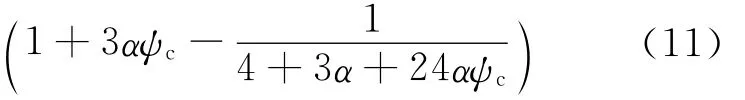
2.2 滿足承載力要求的彎矩調幅限值

結構承載力的大小決定了塑性鉸的轉動能力，而彎矩調幅能力的大小又與塑性鉸的轉動能力有關，在進行彎矩調幅計算時，應該滿足在極限承載能力下塑性鉸的轉動能力不大于梁端截面的極限延性，即μφ≤［μφ］，其中，［μφ］根據（4）式計算，μφ按（11）式求得。因此，可得滿足承載力要求的彎矩調幅限值公式為：

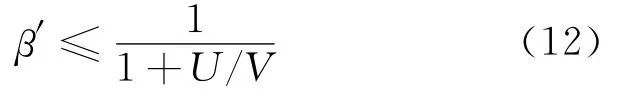
其中

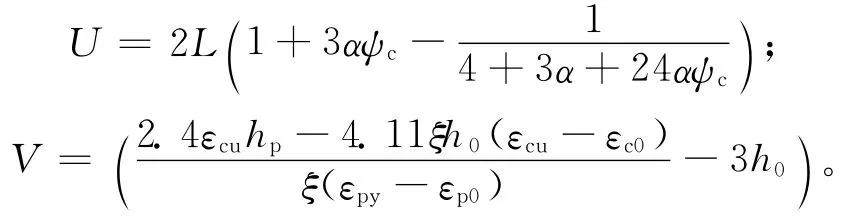
根據文獻［1］的實驗數據，彈性階段半剛性梁端彎矩相當于節點剛性連接計算時的75.2%，因為彎矩調幅是對框架按剛性連接計算時梁端彎矩的降低，因此，彎矩調幅系數β可表示為：

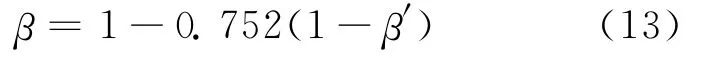
根據文獻［1］，可得滿足承載力要求的彎矩調幅限值如下：KJ－1左梁左、右端分別為β≤0.431，β≤0.452；右梁左、右端分別為β≤0.432，β≤0.421。計算中，α＝0.443，ψc＝0.461，相對受壓區高度見表1。

3 滿足使用要求的彎矩調幅限值

預壓裝配式PC結構和普通鋼筋混凝土結構一樣，應滿足結構的正常使用要求：裂縫寬度不能超過規定限值；正常使用時不出現塑性鉸；正常情況下不能出現太大的撓度。一般情況下，框架只要滿足裂縫寬度的限值要求，則后2個條件就能自動滿足，下面主要討論裂縫寬度對彎矩調幅限值的要求。

3.1 裂縫寬度對彎矩調幅的限值

預壓裝配式PC框架節點具有半剛性的性質，在考慮內力重分布進行彎矩調幅時，其梁端彎矩調幅系數有別于現澆混凝土及預應力混凝土結構。根據現行《混凝土結構設計規范》［4］，裂縫寬度的計算公式可表示為：

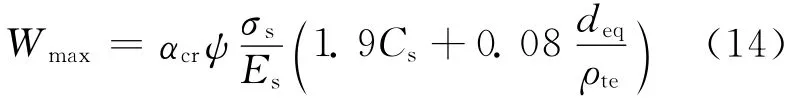
其中，σs為預應力混凝土結構按荷載準永久組合計算時，非預應力鋼筋的應力或預應力鋼筋的應力增量［5］。對于預壓裝配式預應力混凝土結構，在使用荷載作用下，受壓區應力合力點離中和軸的高度約在0.65ξh0處［5］。預應力鋼筋的應力增量σs計算分析如圖5所示。

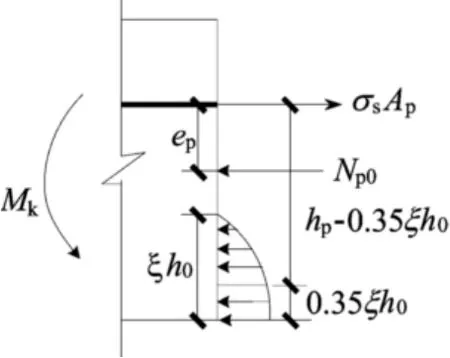
圖5 預應力鋼筋應力增量計算圖

σs與截面受壓區高度ξ的關系可表示為：

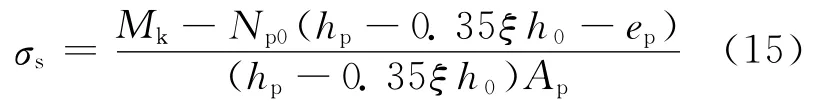
其中，ep為混凝土預壓應力等于0時全部縱向預應力和非預應力筋的合力Np0到受拉區預應力鋼筋的距離。從（14）式可以看出，影響預壓裝配式PC框架的因素有混凝土保護層厚度、受拉區預應力鋼筋的直徑、受拉鋼筋的配筋率、預應力度、截面受壓區高度和初始線應變εc0等。

3.2 裂縫寬度限值［Wmax］及彎矩調幅系數β

根據我國現行規范和工程設計經驗，對不同的裂縫寬度限值可以采取下列彎矩調幅系數，預應力混凝土結構最大裂縫寬度限值［Wmax］＝0.25時，彎矩調幅系數β＝0.15；［Wmax］＝0.20時，β＝0.10；［Wmax］＝0.15時，β＝0.05［6］。對于預壓裝配式PC框架，實驗研究表明［1，7］，框架梁柱節點具有半剛性特點，具有一定的轉動能力，最大裂縫寬度限值可以取為0.20mm，考慮到節點半剛性影響下梁端彎矩的降低，建議彎矩調幅系數β＝0.30。

4 預壓裝配式PC框架彎矩調幅建議

根據上述對預壓裝配式PC框架梁端截面延性及彎矩調幅系數的研究以及文獻［1］中的實驗數據，現提出在豎向荷載作用下預壓裝配式PC框架彎矩調幅的建議：

（1）截面受壓區高度ξ的限制。根據（4）式可得梁端截面延性系數與相對受壓區高度ξ的關系如圖6所示，從圖中可以看出：當受壓區高度ξ＞0.38時，截面延性系數φu／φy＜3.4，因此，梁端截面受壓區高度應滿足ξ≤0.38。

（2）在節點半剛性的影響下，預壓裝配式PC框架彎矩調幅時應滿足承載能力要求即（13）式、正常使用要求即（14）式和裂縫寬度限值0.20mm的要求［8］，如圖7所示，建議預壓裝配式PC框架的彎矩調幅限值［β］按（16）式取用：

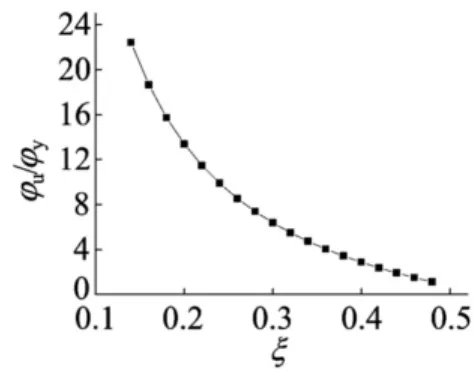
圖6 延性系數φu／φy與ξ的關系

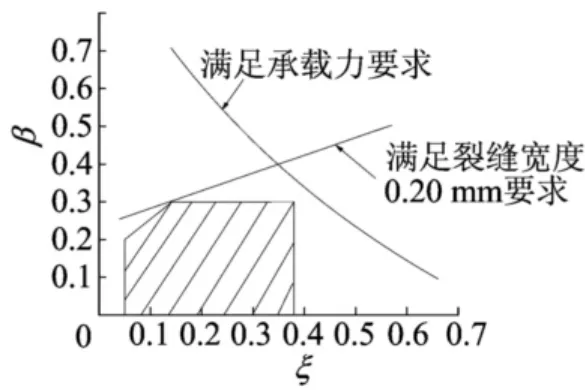
圖7 滿足要求的β與ξ關系圖

（3）框架進行彎矩調幅后，跨中彎矩Mbm應滿足：

其中，Mo為按簡支梁計算的跨中彎矩；Mbl、Mbr為框架梁左端、右端的彎矩。

（4）在預壓裝配式框架設計時，應先對豎向荷載作用下的框架梁端彎矩進行調幅，再與水平荷載產生的彎矩進行組合。

5 結 論

在考慮節點半剛性的影響下，結合一榀單層2跨預壓裝配式PC框架實驗，對其梁端截面延性和彎矩調幅系數進行了研究，得到以下結論：

（1）由截面應變分布符合平截面假定，導出預壓裝配式PC框架梁端截面屈服曲率表達式和極限曲率表達式，計算了梁端截面延性系數并與試驗值進行比較，兩者吻合較好。

（2）導出了預壓裝配式PC框架梁端滿足承載力要求的截面延性系數和彎矩調幅限值，當梁端截面進入極限狀態時，延性系數在4.77～5.34之間，梁端彎矩調幅系數可達0.421～0.452。

（3）導出了預壓裝配式PC框架梁端滿足使用要求的截面延性系數和彎矩調幅限值，考慮節點半剛性的影響和裂縫寬度限值0.20mm的要求，給出了彎矩調幅限值［β］的建議公式，以及彎矩調幅系數限值。

［1］柳炳康，田井峰，張瑜中，等.低周反復荷載下預壓裝配式PC框架延性性能和耗能能力［J］.建筑結構學報，2007，28（3）：74－81.

［2］柳炳康，施法科，劉海濤，等.反復荷載下預壓裝配式框架接合部受力性能［J］.合肥工業大學學報：自然科學版，2005，28（1）：71－74.

［3］蔡建國，馮 健，王蜂嵐，等.考慮節點剛度的預制混凝土框架結構分析［J］.東南大學學報：自然科學版，2009，39（5）：1054－1058.

［4］GB 50010－2010，混凝土結構設計規范［S］.

［5］呂志濤，孟少平.現代預應力設計［M］.北京：中國建筑工業出版社，1998：80－100.

［6］孟少平，呂志濤.預應力混凝土超靜定結構的彎矩調幅系數與抗裂度［J］.建筑結構學報，1999，20（2）：60－67.

［7］柳炳康，宋滿榮，蔣亞瓊，等.預制預應力混凝土裝配整體式框架抗震性能實驗研究［J］.建筑結構學報，2011，32（2）：24－32.

［8］陸惠民，呂志濤.PPC超靜定結構彎矩調幅限值及方法的研究 ［J］.東南大學學報：自然科學版，1999，29（2）：70－75.

Study of moment modification coefficients of prestressed precast concrete frame under the influence of semi－rigid joints

HUANG Shen－jiang， QU Ke－da， ZHANG Ke－qin， LIU Bing－kang
（School of Civil and Hydraulic Engineering，Hefei University of Technology，Hefei 230009，China）

Based on the experimental study of one－layer two－span prestressed precast concrete（PPC）frame，with the consideration of the influence of semi－rigid joints，the factors influencing the ductility coefficients of PPC frame are analyzed，the expressions of yielding and ultimate curvatures at the beam－end sections of PPC frame are derived，and the ductility coefficients at the beam－end sections are computed and compared with experimental results.Taking into consideration the influence of semirigid joints and the limits of crack width，the ductility coefficients and limit value of moment modification with satisfaction to the bearing capacity and operation requirements at the beam－end sections of PPC frame are deduced.The recommended limit value formulas and coefficient limits of moment modification provide a theoretical basis for future design of PPC frame.

prestressed precast concrete（PPC）frame；semi－rigid joint；moment modification

TU378.1；TU313.2

A

1003－5060（2012）11－1514－05

10.3969／j.issn.1003－5060.2012.11.018

2012－04－05；

2012－06－15

國家自然科學基金資助項目（50778060）

黃慎江（1964－），男，江蘇靖江人，合肥工業大學副教授，碩士生導師；

柳炳康（1952－），男，安徽鳳陽人，合肥工業大學教授，博士生導師.

（責任編輯 張淑艷）