一切從定義出發(fā)，再談勻速圓周運動速度方向的變化率

王愛華

（江蘇省東海中等專業(yè)學校，江蘇 東海 222300）

最近筆者閱讀了本刊2011年第8期沈老師撰寫的《關(guān)于向心加速度的物理意義及什么是描述速度方向變化快慢的物理量的思考》一文，發(fā)現(xiàn)許多看似簡單的物理問題，都不能貿(mào)然做出結(jié)論.順著沈老師文章的指引，筆者又拜讀了本刊2011年第2期湯老師和龔老師的兩篇文章.正如沈老師所言，二者的結(jié)論截然相反.

縱觀3篇文章，湯老師認為在勻速圓周運動中，向心加速度不能反映速度方向變化的快慢，龔老師認為向心加速度可以反映速度方向變化的快慢，而角速度不可以；沈老師認為向心加速度不如角速度來得更準確.

誰都有些道理，誰的道理又都不是那么強而有力.

研讀了這3篇文章，它們的共同點就是忽略了物理量的矢量特性.有的是把矢量與標量混同（例如角速度ω與角速度的大小ω，前者是矢量，后者是標量.在使用時，3位教師都沒有加以區(qū)別）；有的是沒有用科學的方法來表示矢量的方向（例如沈老師在二維笛卡爾坐標系里，用速度與橫軸之間的夾角φ來表示速度方向，然而表示方向的量，本身卻是標量）.

看來要把問題說得明白，只有從各物理量的定義出發(fā)，用矢量分析的方法才能弄清楚各物理量間的關(guān)系.

物理量分為標量和矢量，標量是只有大小沒有方向的物理量，而矢量是既有大小又有方向的物理量.標量的變化量同樣是標量，是沒有方向的；標量對時間的導數(shù)稱為標量的變化率，同樣沒有方向，也是標量，其絕對值表示標量的變化快慢.矢量的變化量仍然是矢量，是有方向的，從前一個矢量的箭頭指向后一個矢量的箭頭（符合矢量三角形法則）；矢量對時間的導數(shù)稱為矢量的變化率，也是矢量，它的方向為原矢量矢端曲線的切線方向，且指向?qū)猼值增大的方向.矢量變化率的模是標量，沒有方向，例如位移矢量的變化率是速度矢量，而速度的大小稱為速率，則是標量，只有大小，沒有方向.

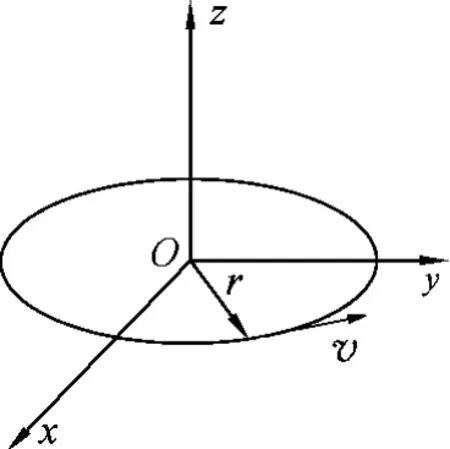
圖1

在圓周運動中（如圖1），位移矢量可以表示為

r＝Rn（R 為常量，n為徑向單位矢量函數(shù)）.

位移矢量的變化率（速度）為

v是標量函數(shù)，τ是切向單位矢量函數(shù).

速度變化率（加速度）為

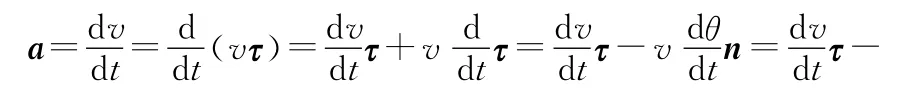
其中切向加速度為

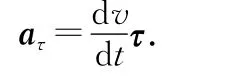
徑向加速度（向心加速度）為

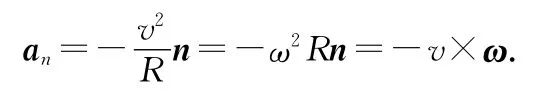
如果是勻速圓周運動，則有切向加速度為

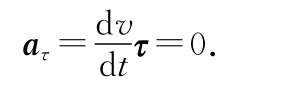
徑向加速度（向心加速度）為

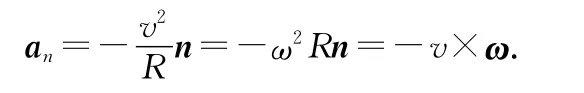
an＝是恒定標量，表示速度變化的快慢，量綱為［LT－2］，n為單位徑向單位矢量函數(shù).

在圓周運動中，角位移可以表示為

θ＝θk.（θ為標量函數(shù)，k為z軸單位矢量）

角位移矢量的變化率（角速度）為

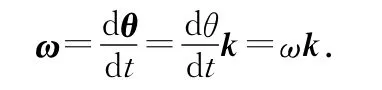
ω是一個方向恒定的矢函數(shù).

在勻速圓周運動中，則有角速度ω＝ωk，是一個恒定的矢量，角速度的大小（也稱角頻率）ω是恒定標量，量綱為［T－1］.

在圓周運動中，速度的方向為τ（切線方向單位矢量函數(shù)），其變化率為

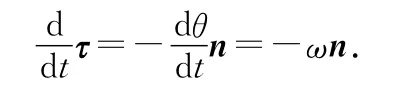
ω就是是勻速圓周運動的角速度大小，是一個恒定的標量，可以表示勻速圓周運動速度方向變化的快慢，量綱為［T－1］，n表示徑向單位矢量函數(shù).

綜上所述，在物體在做勻速圓周運動時，速度變化率就是向心加速度，其大小（亦即速度變化的快慢）為恒定標量，量綱為［LT－2］，方向為－n（n為徑向單位矢量函數(shù)）.速度方向的變化率沒有專門物理量與之對應，其大小（亦即速度方向變化快慢）為恒定標量ω（角速度的大小），量綱為［T－1］，方向為－n（n為徑向單位矢量函數(shù)）.

原來在勻速圓周運動中，速度方向的變化率ω2R（與速度變化率方向相同，量綱不同）的方向與向心加速度相同，都指向圓心，大小（亦即速度方向變化的快慢）卻與角速度大小ω有關(guān).這個左右都沾邊的物理量，在物理學中沒有專門名稱（說它是向心加速度，量綱不同；說它是角速度，方向又不同），也沒有專門的動力學量與之對應（例如，向心加速度有向心力與之對應）.正如沈老師所言，它是一個無實際價值的物理量，在一般的教學中，我們要盡量回避它.在避不開時，我們又必須依據(jù)它的定義，沿著數(shù)學推導的路徑，徹底地弄清它.如果一味回避，或者從一些想當然的結(jié)論出發(fā)，必然會使許多概念都含混不清.

1 湯家合.對向心加速度物理意義的探討.物理教師（教學研究版），2011（2）.

2 龔勁濤，魏標.加速度能表示速度方向變化快慢嗎？物理教師（教學研究版），2011（2）.

3 沈瑞清.關(guān)于向心加速度的物理意義及什么是描述速度方向變化快慢的物理量的思考.物理教師（教學研究版），2011（8）.