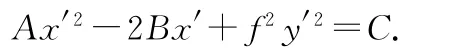物理競(jìng)賽中的橢圓

鄭 金

（凌源市職教中心，遼寧 朝陽(yáng) 122500）

在數(shù)學(xué)中，到兩個(gè)定點(diǎn)的距離之和等于常數(shù)的點(diǎn)的集合為橢圓.當(dāng)以長(zhǎng)軸為x軸時(shí)，橢圓的標(biāo)準(zhǔn)方程為

橢圓是一種圓錐曲線，在平面上到定點(diǎn)F的距離與到定直線l的距離之比為常數(shù)e的點(diǎn)的集合是橢圓.偏心率為小于1的正數(shù)；近焦點(diǎn)到準(zhǔn)線的距離即焦準(zhǔn)距為在以橢圓的遠(yuǎn)焦點(diǎn)為極點(diǎn)，以長(zhǎng)軸所在直線為極軸的極坐標(biāo)系中，橢圓的極坐標(biāo)方程為r＝若設(shè)半通徑即半正焦弦為ρ0，則由定義可知ρ0因此

橢圓的光學(xué)性質(zhì)：從橢圓的一個(gè)焦點(diǎn)發(fā)出的光線，經(jīng)橢圓反射后，反射光線經(jīng)過(guò)另一個(gè)焦點(diǎn).由反射定律知，橢圓上任一點(diǎn)的法線平分該點(diǎn)對(duì)兩個(gè)焦點(diǎn)的張角.即橢圓上任一點(diǎn)的法線平分焦點(diǎn)三角形的頂角.

1 力學(xué)中的橢圓

某些行星和衛(wèi)星等天體在萬(wàn)有引力作用下的運(yùn)動(dòng)軌跡多為橢圓.

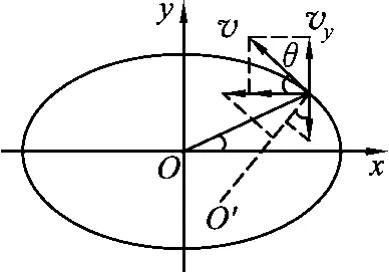
圖1

解析：把質(zhì)點(diǎn)的橢圓運(yùn)動(dòng)視為兩個(gè)沿坐標(biāo)軸方向的同一頻率的簡(jiǎn)諧運(yùn)動(dòng)的疊加，設(shè)t＝0時(shí)x＝a，則y＝0，因此質(zhì)點(diǎn)的運(yùn)動(dòng)方程為

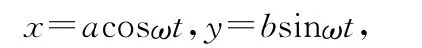
分速度為vx＝－aωsinωt，vy＝bωcosωt，所以

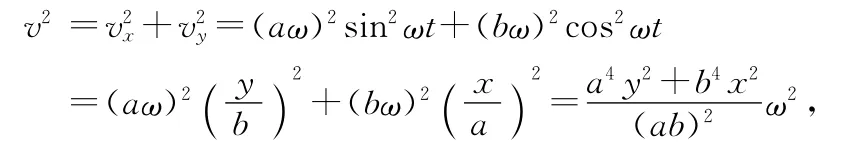
對(duì)分速度求導(dǎo)數(shù)得分運(yùn)動(dòng)的加速度為

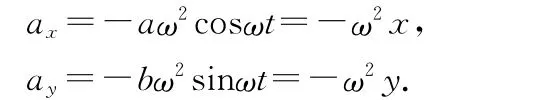
對(duì)應(yīng)的回復(fù)力分別為Fx＝－mω2x，F(xiàn)y＝－mω2y，設(shè)曲率半徑與Fy方向夾角為θ，則合速度與vx方向夾角為θ.可知法向力為

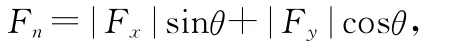
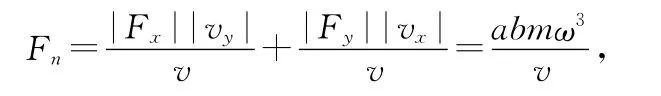
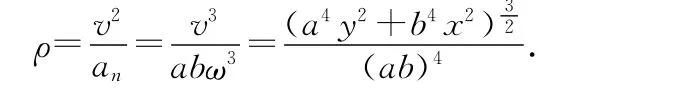
還可利用極坐標(biāo)方程求解，在圖1中，在以左焦點(diǎn)為極點(diǎn)，以x軸為極軸的極坐標(biāo)系中，由于左焦點(diǎn)為遠(yuǎn)焦點(diǎn)，則橢圓的極坐標(biāo)方程為對(duì)于右頂點(diǎn)，r＝a＋c，θ＝0，所以

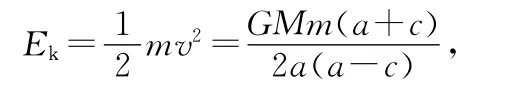
另解：在萬(wàn)有引力作用下，物體的機(jī)械能和角動(dòng)量都守恒.由于在遠(yuǎn)地點(diǎn)和近地點(diǎn)的速度都與矢徑垂直，則角動(dòng)量為L(zhǎng)＝mv·r，機(jī)械能總量為

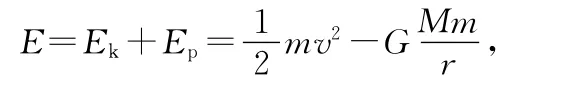
遠(yuǎn)、近地點(diǎn)的矢徑長(zhǎng)度為方程的兩個(gè)根，由韋達(dá)定理可知

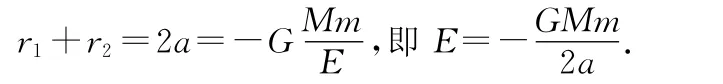
2 熱學(xué)中的橢圓

例2.（第15屆全國(guó)中學(xué)生物理競(jìng)賽預(yù)賽題）1mol理想氣體緩慢地經(jīng)歷了一個(gè)循環(huán)過(guò)程，在p－V圖中這一過(guò)程是一個(gè)橢圓，如圖2所示.已知此氣體若處在與橢圓中心O′點(diǎn)所對(duì)應(yīng)的狀態(tài)時(shí)，其溫度為T(mén)0＝300k.求在整個(gè)循環(huán)過(guò)程中氣體的最高溫度T1和最低溫度T2各是多少？

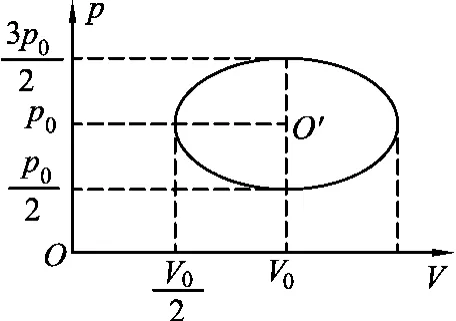
圖2

與橢圓相切的等溫線，所對(duì)應(yīng)的溫度為循環(huán)過(guò)程的最高或最低溫度.

假如畫(huà)圖時(shí)取橫縱坐標(biāo)軸的刻度相等，則橢圓變?yōu)檎龍A，那么圓心過(guò)第一象限的角分線，而等溫線與圓周的切點(diǎn)在角分線上，可知離原點(diǎn)最遠(yuǎn)的切點(diǎn)坐標(biāo)為

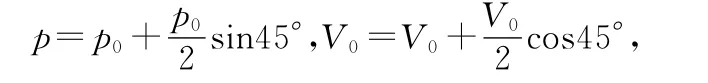
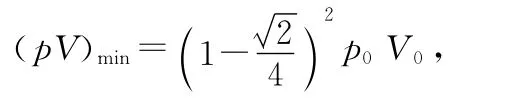
易知另一個(gè)切點(diǎn)即離坐標(biāo)原點(diǎn)最近的切點(diǎn)的坐標(biāo)為

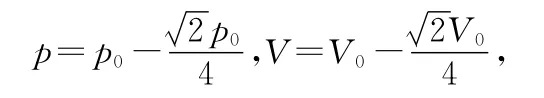
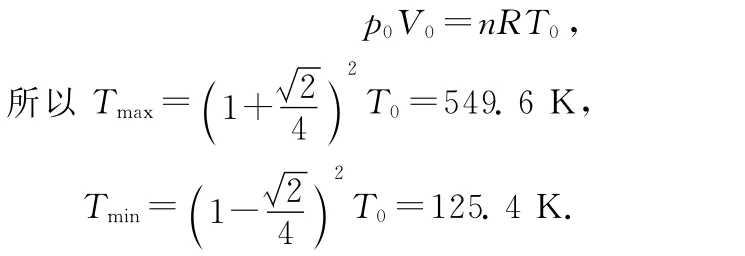
拓展：若循環(huán)過(guò)程沿順時(shí)針?lè)较颍瑒t氣體做功情況如何？

解析：因循環(huán)過(guò)程沿順時(shí)針?lè)较颍瑒t氣體對(duì)外做功，數(shù)值上等于橢圓的面積，由公式S＝πab得

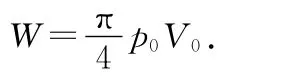
3 電學(xué)中的橢圓

例3.真空中有一固定點(diǎn)電荷，帶正電為Q，另一點(diǎn)電荷帶負(fù)電為q，質(zhì)量為m，繞Q做橢圓運(yùn)動(dòng)，Q位于橢圓的一個(gè)焦點(diǎn)上，q與Q的最大距離為a，最小距離為b，如圖3所示，求：（1）q繞Q運(yùn)動(dòng)的周期；（2）負(fù)電荷在距正電荷最近點(diǎn)和最遠(yuǎn)處的速率；（3）若負(fù)電荷在距正電荷最遠(yuǎn)處獲得能量而繞其做圓周運(yùn)動(dòng)，它獲得的能量是多大？

解析：（1）由于在橢圓運(yùn)動(dòng)過(guò)程中q只受Q的庫(kù)侖引力，跟行星繞恒星做橢圓運(yùn)動(dòng)時(shí)所受的萬(wàn)有引力相似，則帶電粒子的橢圓運(yùn)動(dòng)也遵循開(kāi)普勒第三定律，即電荷q做橢圓運(yùn)動(dòng)周期的平方與其長(zhǎng)半軸的3次方成正比.由題意知橢圓的半長(zhǎng)軸為因此橢圓運(yùn)動(dòng)周期等于q繞Q做半徑為的勻速圓周運(yùn)動(dòng)的周期.由得

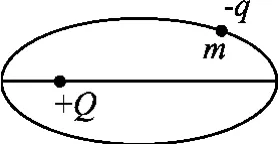
圖3

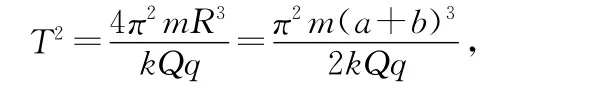
（2）由角動(dòng)量守恒有mv1·b＝mv2·a，由能量守恒定律有

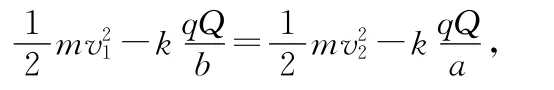
解得近點(diǎn)和遠(yuǎn)點(diǎn)的速率分別為

（3）設(shè)負(fù)電荷繞正電荷做半徑為a的圓周運(yùn)動(dòng)的速度為v3，則有此時(shí)具有的動(dòng)能為

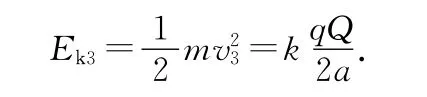
所以負(fù)電荷在遠(yuǎn)點(diǎn)獲得的能量為

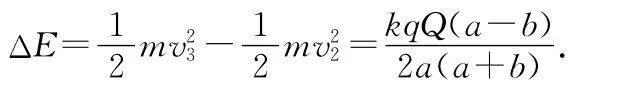
4 光學(xué)中的橢圓

例4.如圖4所示，真空中的一束平行光線沿平行于長(zhǎng)軸的方向射入折射率為n的旋轉(zhuǎn)橢球體介質(zhì)中，為使所有光線都嚴(yán)格會(huì)聚于橢圓旋轉(zhuǎn)體的右焦點(diǎn)，試求出偏心率應(yīng)滿足的關(guān)系.

解析：以主軸為極軸，右焦點(diǎn)為極點(diǎn)，建立極坐標(biāo)系如圖5所示，極軸方向向右，從左準(zhǔn)線開(kāi)始沿主軸向右傳播的一束平行光的光程可表示為

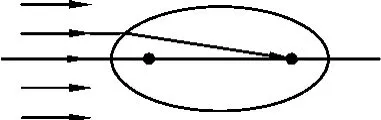
圖4

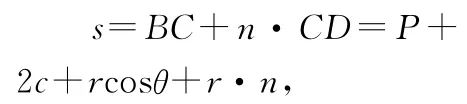
已知cosθ＜0，則以近焦點(diǎn)為極點(diǎn)，以長(zhǎng)軸所在直線為極軸的極坐標(biāo)系中，極坐標(biāo)方程為故

圖5

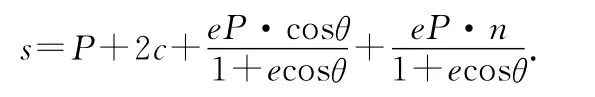
由費(fèi)馬原理可知，光程差為定值，則后兩項(xiàng)之和應(yīng)該為定值，即

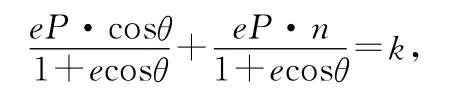
化簡(jiǎn)得ecosθ（P－k）＝k－ePn.

為使θ取任何值時(shí)等式都成立，須使cosθ的系數(shù)為零，即k＝P，所以P（1－en）＝0，解得

例5.把一個(gè)球形框架放在凸透鏡的一側(cè)，使球心位于主光軸上距光心兩倍焦距處，球半徑r＜f，試推斷這個(gè)球形框架通過(guò)透鏡所成的像的形狀是球形體還是橢球體？

解析：以光心為坐標(biāo)原點(diǎn)，主光軸為x軸，建立直角坐標(biāo)系如圖6所示.設(shè)圓心坐標(biāo)為（c，0），則圓的方程為

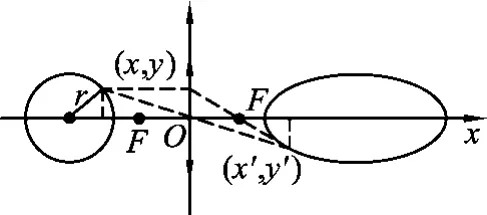
圖6

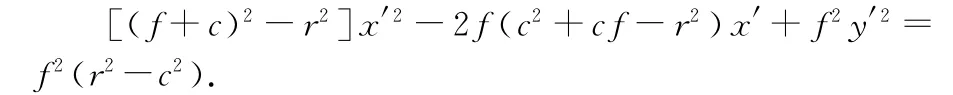
令A(yù)＝（f＋c）2－r2，B＝f（c2＋cf－r2），C＝f2（r2－c2），則有