球籠式等速萬向節軸向間隙形成的周向間隙分析

劉庭洋，郭常寧，石寶樞，楊洪興

(1.上海交通大學 機械與動力工程學院，上海 200240；2.浙江眾達傳動股份有限公司，浙江 金華 321025)

球籠式等速萬向節是前輪驅動轎車的關鍵部件之一，其可以實現成夾角的輸入軸與輸出軸的等角速度傳動。然而由于運動副配合需要[1]及其制造和裝配等方面的原因，其各零件之間存在間隙，其中軸向間隙以及由其形成的周向間隙是造成萬向節內部各零件竄動與沖擊以及使用壽命降低的重要原因。文獻[2]對三球銷式等速萬向節周向間隙的計算公式進行了推導，給出了分析周向間隙的基本方法；文獻[3]對球籠式等速萬向節周向間隙進行了研究，分析了在給定制造誤差條件下周向間隙的變化規律；但這些研究均未涉及軸向間隙形成周向間隙的條件及計算方法。在此，針對球籠式等速萬向節的結構和運動形式，計算了任意擺角和轉角下軸向間隙形成的周向間隙，并分析了周向間隙隨擺角和轉角的變化規律。

1 球籠式等速萬向節的結構

圖1為擺角為0時球籠式等速萬向節的縱截面圖和橫截面圖。球籠式等速萬向節由鐘形殼、星形套、保持架和6個均布鋼球構成。鐘形殼和星形套上各有6條半雙心弧溝道。星形套、鐘形殼溝道曲率中心A和B等距地偏置在萬向節傳動中心O的兩側，偏心距為e；鋼球1的球心C在星形套中繞著A做圓周回轉運動，其回轉半徑為R；6個鋼球由保持架約束，其球心均在D-D平面內。球籠式等速萬向節有兩組繞O點轉動的球面副：一組為星形套外球面與保持架內球面組成的球面副，另一組為鐘形殼內球面與保持架外球面組成的球面副。

圖1 周向間隙的形成

如圖1所示，星形套初始時位于虛線位置，其球面中心與鐘形殼及保持架球面中心重合于O點，鋼球1與星形套溝道接觸于E點。由于在星形套外球面與保持架內球面間存在徑向間隙[4]，假設鐘形殼和保持架不動，星形套可在E點與鋼球1脫離接觸，沿OA方向移動到實線位置，此時星形套外球面碰到保持架內球面，星形套溝道曲率中心也由A點移動到A0點。星形套沿OA方向移動的最大位移即為星形套與保持架間的軸向間隙δt(δt=AA0)。顯然星形套移動時未與6個鋼球發生干涉。星形套移動后，鋼球與星形套溝道之間形成了周向間隙，星形套就可以相對轉動。

鐘形殼不動，星形套由虛線位置沿AO方向移動，顯然星形套會與6個鋼球保持接觸，推動鋼球和保持架一起移動，直至保持架外球面碰到鐘形殼內球面為止。星形套沿AO方向移動的最大位移即為鐘形殼與保持架間的軸向間隙δk，星形套移動后鐘形殼與鋼球之間同樣形成了周向間隙。形成周向間隙的方式可分為鐘形殼固定不動，星形套移動；或星形套固定不動，鐘形殼移動，星形套或鐘形殼移動時都只能沿其軸線方向移動。

2 空間坐標系的建立

為了便于計算和分析需建立空間坐標系，作如下假設：(1)鐘形殼、星形套的雙心弧溝道為理想溝道，不存在制造誤差；(2)假設鐘形殼不能擺動，星形套可上下擺動，其他情況可類似推導。

如圖2所示，C點為鋼球1既未擺動又未轉動時的球心位置，此時，星形套、保持架及鐘形殼三者的軸線重合于軸Ⅰ，鋼球1擺動α角后球心由C點擺到了C0點位置，保持架和星形套的軸線也分別繞O點擺到了軸Ⅱ及軸Ⅲ的位置，星形套溝道中心也由A點擺動到A1點，規定此時的擺動方向為正。

圖2 空間坐標系

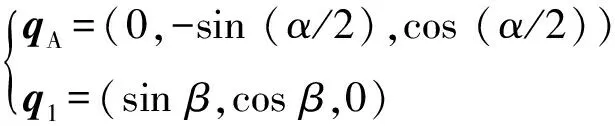
(1)

在△A1OC1中A1C1=R，經計算得

(2)

由(1)和(2)式得

(3)

(4)

3 α≠ 0時周向間隙的產生

(5)

或

(6)

由圖2知，第i+1個鋼球的轉角比第i個鋼球的轉角超前了60°，聯系(3)式即可得φi+1=φi(β+60°)，所以萬向節轉動60°后min{φ1,φ2,φ3,φ4,φ5,φ6}變成了min{φ2,φ3,φ4,φ5,φ6,φ1}，即min{φi}以60°為一變化周期。

做出α>0時φ1隨β的變化曲線可得

φ1<90°，β=0～60°，

(7)

做出α<0時φ3隨β的變化曲線同樣可得

φ3<90°，β=0～60°。

(8)

由(7)和(8)式可知，β=0～60°時，min{φi}<90°，由于min{φi}以60°為一變化周期，所以在任意α，β角下min{φi}<90°都成立，即(6)式恒不能滿足。

當α>0，β=0～60°時，經比較可得max{φi}=max{φ3,φ4}。圖3為α>0時φ3,φ4隨β的變化曲線，圖3中兩條曲線的上半部分即為max{φi}。

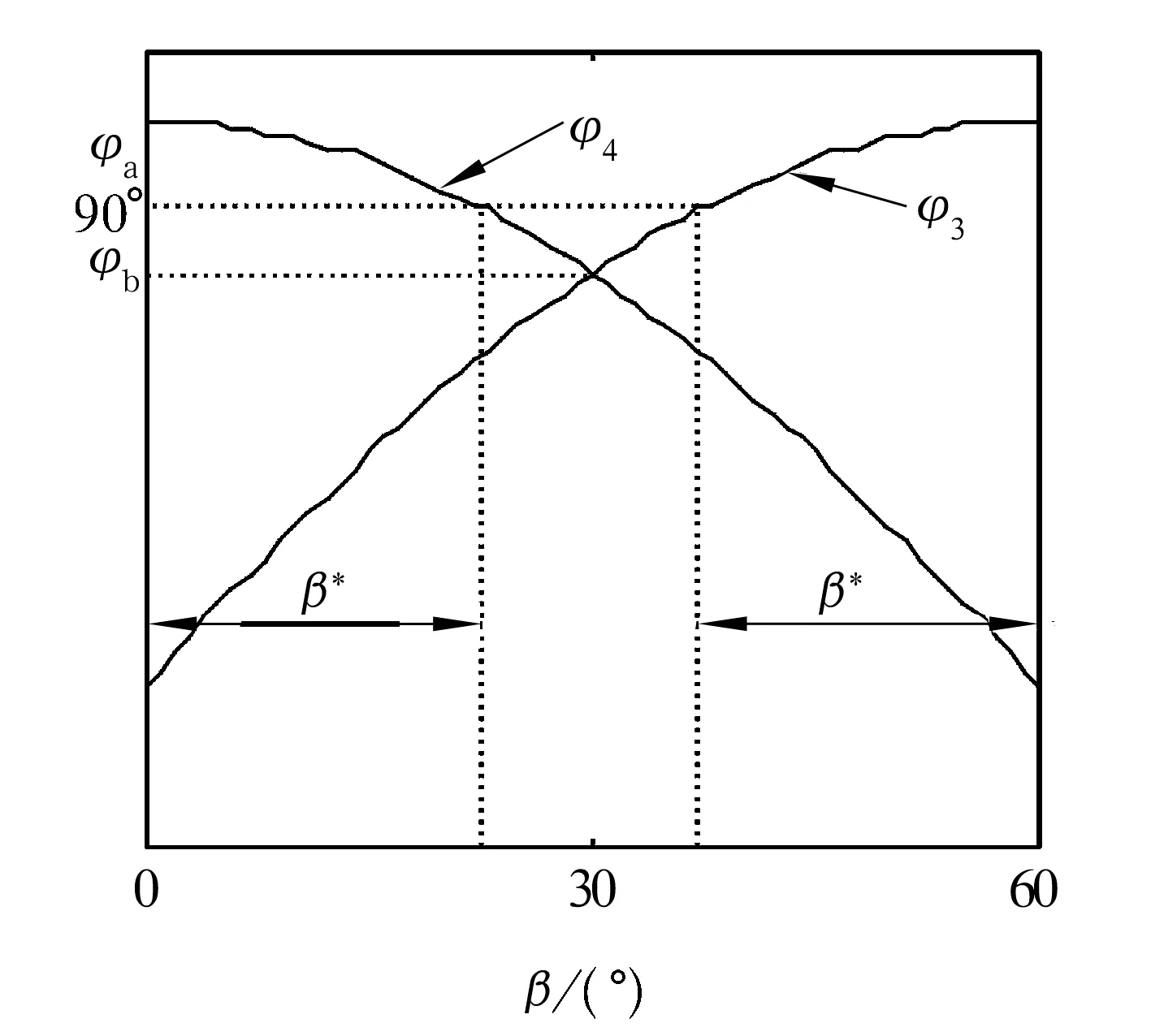
圖3 α>0時鋼球3，4的φ角隨β的變化曲線

由圖3可知，φa=φ4(0)=φ1(180°)；φb=φ4(30°)=φ1(210°)。則α>0，β=0～60°時max{φi}<90°等價于

(9)

β*滿足φ4(β*)=φ1(180°+β*)=90°，代入(3)式可得

(10)

類似可推導得max{φi}以60°為一周期，顯然max{φi}關于α=0對稱，這是由于萬向節結構的對稱性所致。根據max{φi}的變化特點聯立(3)，(4)，(9)，(10)式得

(11)

或

(12)

設使(11)～(12)式成立的(α,β)屬于集合Ω={(αk,βk)}，k=0，1,…,n。當m>0,(α,β)∈Ω時，(5)式成立，即星形套可沿OA1方向移動且不與6個鋼球發生干涉，在星形套外球面碰到保持架內球面后不再移動。

當(α,β)不屬于Ω或m<0,(α,β)∈Ω時，(5)～(6)式均不能成立，則星形套無論沿OA1或A1O方向移動至少會與一個鋼球發生干涉，即星形套會帶動此鋼球一起移動，由于萬向節擺動后鐘形殼溝道與星形套溝道是空間交錯的[5]，所以星形套推動鋼球移動時，鋼球又會與鐘形殼溝道發生干涉，這就使得星形套實際上無法移動。總之，只有當(α,β)∈Ω時，星形套才能沿OA1方向移動。

用類似方法可推得，只有當(α,β)∈Ω時，鐘形殼才能沿BO方向移動，直至鐘形殼內球面碰到保持架外球面為止。

4 軸向間隙形成的周向間隙的計算

如圖1所示，剖切線W-W與鋼球1固連，萬向節擺動α角轉動β角后，剖切線W-W剖得的剖面Λ即為圖4(圖中鐘形殼未畫出)。O′y′z′面即位于面Λ上。設(α,β)∈Ω，如圖5所示，星形套可沿OA1方向由虛線位置移動到相對于保持架的極限位置，相應地星形套溝道曲率中心A1移動到A3，星形套E端移動到E′位置，顯然EE′//OA1。星形套與保持架間的軸向間隙δt=|EE′|。建立動坐標系O″x″y″z″，坐標原點O″位于A3點，x″軸與x′軸平行(未畫出)，y″軸與直線A3C1重合，z″軸由右手定則產生，則O″x″y″z″坐標系可看作是O′x′y′z′坐標系沿z′軸平移位移d后，再繞移動后的x′軸旋轉90°-γ2角后所得。

O″x″y″z″坐標系到O′x′y′z′坐標系的四階變換矩陣為

(13)

式中：d=e+δt。

過點E，E′作垂線分別交軸Ⅲ于F，F′點。由幾何關系可得

(14)

式中：Bt為星形套外球面中心至左端面的距離；Rt為星形套外球面徑和保持架內球面徑的公稱值；εt為星形套與保持架間的徑向間隙。

在△A1A3C1中，∠A3A1C1=180°-φ1，設A3C1=l，又A1C1=R，A1A3=δt，由余弦定理知

(15)

式中：l為星形套的溝道曲率中心與鋼球球心的距離。

如圖4所示，在O′y′z′坐標系中，線段A3C1與線段A1C1在y′軸上的投影相等，即

lsinγ2=Rsinφ1，

則

(16)

實際生產過程中一般使用周向間隙角來評價周向間隙的大小，周向間隙角等于周向間隙除以接觸點到驅動軸線的距離。為了計算周向間隙角，應確定鋼球哪個部位與星形套之間的間隙最小，作無數條平行于x′軸的直線分別交同一側的鋼球和星形套溝道于J1，K1，J2，K2，…，求得所有線段中|JK|的最小值即為鋼球與星形套的最小間隙。如圖4所示可用一個簡便的方法來計算，過點A3作垂直于Λ面的剖面將鋼球與星形套切成無數個面，計算出每個剖面上圓和雙心弧的最小間隙，比較這些間隙值，最后得到鋼球與星形套之間的最小間隙。根據星形套溝道的特點，可知過直線A3C1所做的剖面上，圓和雙心弧的最小間隙即是鋼球與星形套之間的最小間隙。

圖4 軸向間隙的計算

沿直線A3C1作垂直于Λ平面的剖面φ1，如圖5所示，鋼球與星形套溝道在φ1面上的投影分別為圓1和雙心弧1，圓1的圓心為C1，Q點為與雙心弧1相切的圓的圓心。雙心弧的溝道曲率半徑為rs,雙心弧溝道偏心距為es，鋼球的半徑為r。作平行于x″軸的直線分別交圓1和雙心弧1于G′，G點和H，H′點，交y″軸于M點。

圖5 圓和雙心弧間的間隙示意圖

由圖5可知，圓1的方程為

x″2+(y″2-l)2=r2，

(17)

x″>0時，雙心弧1的方程為

(18)

在O″x″y″坐標系中，設G點縱坐標為y″，由(17)～(18)式可得

(19)

令Δl=GH,由(19)式可得函數Δl為

(20)

對Δl求導

(21)

將(21)式代入(20)式，得最小間隙為

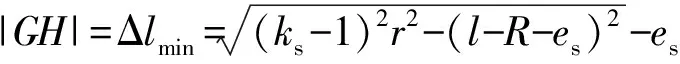
(22)

將(21)式代入(19)式可得G點在O″x″y″z″坐標系上的坐標為

(23)

在圖4中過點M作垂直于z′軸的剖面φ2，φ2面與z′軸交于N點，顯然φ2面平行于O′x′y′面。由于直線HH′∥x′軸，所以直線HH′位于φ2面上，即點G，G′和點H，H′位于φ2面上，如圖6所示。鋼球與星形套溝道在φ2面中的投影分別為圓2、雙心弧2，圓2的圓心為C7。線段GH的長度即是鋼球與星形套的最小間隙，其局部放大圖如圖6b所示。

通過轉換矩陣M將G點由O″x″y″z″坐標系轉換到O′x′y′z′坐標系上，聯立(13)，(16)，(23)式可解得G點在O′x′y′z′上的坐標為

(24)

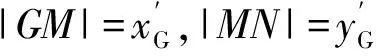
(25)

圖6 圓和雙心弧間的周向間隙計算示意圖

(26)

由(24)～(26)式得

(27)

|GN|即為接觸點G到星形套軸線的距離。在曲邊△GPQ中，∠GQP=90°，∠HGP=ω1，∠HGQ=ω2，由余弦定理知|GQ|=|GH|cosω2=|GR|cos(ω2-ω1)，則鋼球與星形套之間的周向間隙即弧長|GP|為

(28)

所以星形套與鋼球之間的周向間隙角

(29)

5 計算示例與分析

現以星形套與鋼球之間的周向間隙角θ1為例進行分析，鐘形殼與鋼球之間的周向間隙角可作類似分析。某球籠式等速萬向節結構參數為：εt=0.07 mm，Rt=29.35 mm，Bt=10.3 mm，rs=9.08 mm，es=0.246 4 mm，r=8.731 5 mm，R=30.4 mm，e=4.5 mm。由(11)式可知，|α|<16.84°時軸向間隙與周向間隙存在，由(14)式可得軸向間隙δt=0.099 3；由(12)式知，16.84°<|α|<19.47°時，只有在β位于某些區間時軸向間隙與周向間隙存在，隨著|α|的增大，這些區間逐漸變小，當|α|>19.47°時軸向間隙與周向間隙均不存在。

圖7 周向間隙角隨軸向間隙的變化規律

當α=0～16.84°，β=0～360°時，單個鋼球θ1的變化率k1的三維變化規律如圖8所示。由圖可知，萬向節未擺動時，k1為一條直線，隨著萬向節擺角的逐漸增大，k1由一條直線變為余弦曲線且曲線的波幅越來越大。當α=16.84°，β=0或360°時，k1達到最大值31.42；當α=16.84°，β=180°時，k1達到最小值1.078。萬向節轉動一周，k1隨β角的變化出現一次波動，k1在β=0或360°(以鋼球1的起始角度為0)時取得最大值，這是由于鋼球的φ角在β=0或360°時取得極小值。將(15)式化為二階麥克勞林公式為

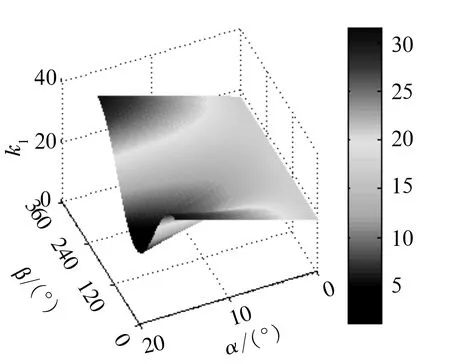
圖8 單個鋼球k1的三維變化規律

(30)

由(30)式可知，鋼球的φ角取得極小值時，一次項系數cosφ取得極大值，這就使得星形套溝道曲率中心與鋼球球心的距離l的變化率取得極大值，而k1與l的變化率成正比；k1在β=180°時取得極小值，這是由于鋼球的φ角在此時取得極大值，同理可知，此時l的變化率取得極小值。

考慮到6個鋼球相互制約，因而，周向間隙角θ1隨軸向間隙δt的實際變化率應為6個鋼球θ1的變化率k1的最小值。圖9為α=0～16.84°，β=0～360°時，實際變化率k1隨α和β的變化規律。由圖9知，α=0時實際變化率k1為一條直線且最大值為16.88，隨著α的增大，實際變化率k1減小，當α接近16.84°，k1趨近于零。萬向節轉動一周時，實際變化率k1共出現6次波動，其中最大值分別出現在β=30°，90°，150°，210°，270°及330°(以鋼球1的起始角度為0)位置，最小值分別出現在β=0，60°，120°，180°，240°及300°位置。由θ1=k1δt可知，隨著α的增大實際變化率k1減小，意味著軸向間隙引起的實際周向間隙角θ1隨著α的增大而減小，所以增大擺角可有效減小由軸向間隙形成的周向間隙；實際變化率k1的6次波動即是軸向間隙引起的實際周向間隙角θ1的6次波動，而這6次波動正是導致萬向節轉動時內部各零件竄動與沖擊以及使用壽命降低的重要原因。總的周向間隙角θ=θ1+θ2，θ2與θ1有著相同的變化規律，只是大小不同。

圖9 實際變化率k1的變化規律

6 結論

(1)當擺角α大于某一值(20°左右)時，軸向間隙與周向間隙角均為零，在擺角、轉角不變時，周向間隙角隨軸向間隙變化的曲線為一條凸曲線，在軸向間隙的實際范圍內，該曲線可近似為一條直線。

(2)單個鋼球的周向間隙角θ的變化率k隨著擺角α和轉角β的變化而變化。當α=0時，k為一定值；當α≠0時，k隨著β的變化呈余弦曲線變化；k在β為0和360°時取得極大值，在180°時取得極小值。

(3)實際變化率k隨著α的增大總體上有一個由大變小的趨勢。萬向節轉動一周，實際變化率k共出現6次波動，其中波峰分別出現在β=30°，90°，150°，210°，270°及330°位置上，其中波谷分別出現在β=0，60°，120°，180°，240°和300°位置上，而這6次波動是造成萬向節轉動時內部各零件竄動與沖擊以及使用壽命降低的重要原因。