基于ANSYS 12.0的靜壓軸承雙向流固耦合分析

沈棟平，郭波，王發峰

(1.富奧汽車零部件股份有限公司 研發中心，長春 130013；2.長春設備工藝研究所，長春 130012；3.中國第一汽車股份有限公司 技術中心，長春 130011)

球磨機作為將固體物料細化制粉的重要設備，廣泛應用于冶金、化工、水泥、陶瓷、建筑、電力、醫藥以及國防工業等領域。軸承是球磨機的關鍵部件，其工作的穩定性直接影響球磨機能否正常運行。由于靜壓軸承具有可靠性高、使用壽命長、能耗小及承載能力大等特點在大型球磨機上廣泛應用。下文針對某大型球磨機的回轉部靜壓軸承運用ANSYS 12.0軟件的流固耦合功能進行雙向流固耦合分析，計算中空軸﹑軸瓦結構與油膜流體相互作用下，結構的受力情況，校核該靜壓軸承的承載能力。

1 流固耦合

1.1 概述

流固耦合是研究變形固體在流場作用下的各種行為以及固體行為對流場影響這二者交互作用的一門學科[1]。流固耦合力學的重要特征是兩相介質之間的交互作用(Fluid Structure Interaction), 變形固體在流體載荷作用下會產生變形或運動，而變形或運動又反過來影響流場，從而改變流體載荷的分布和大小。流固耦合問題可由其耦合方程來定義，這組方程的定義域同時有流體域與固體域，而未知變量含有描述流體現象的變量及描述固體現象的變量。根據變形協調條件和動力學協調條件來建立耦合方程。動力學協調條件即力平衡條件，耦合界面上流體和閥片的應力必須在法線方向平衡。可采用任意拉格朗日歐拉(Arbitrary Lagrange-Euler，ALE)法進行流固耦合求解，即在流體區域中采用Euler單元，對固體區域內用Lagrange單元，并在統一的 ALE 坐標系下進行求解，使得流體模型中的流固界面總是跟隨固體的變形而改變。

1.2 控制方程[2]

1.2.1 流體區域

ALE描述法是引入一個可以獨立于現時構形和初始構形運動的參考構形，記作Ωζ。在物體的變形和運動過程中，參考構形是始終固定不動的，而現時構形和初始構形都相對于參考構形運動。為了確定參考構形中各參考點的位置，引入參考坐標系Oζ1ζ2ζ3，參考構形中各點的位置由其在參考坐標系中的位置矢量ζ確定。ALE描述下，物理量F=F(ζ,t)的物質導數表示為

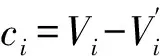
式中：ρ為流體的密度，kg·m-3；σij為Couchy應力張量的分量，kg·m-1·s-2，其中i，j為自由標號，因為求解的物理量一般為三維，取值通常都是1，2，3。fi為體力分量，m·s-2。Couchy應力張量的分量σij可以表示為

σij=-pδij+2μVi,j，

式中：p為壓力，Pa；μ為流體的動力黏性系數，kg·m-1·s-1；δij為應力張量的一個分量；Vi,j為變形速度張量的分量，即

1.2.2 固體區域

由于在固體部分的運動學描述仍然采用Lagrange描述方法，由彈性力學基本理論可以得到固體區域的基本方程組為：

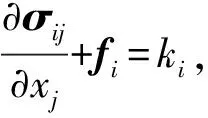
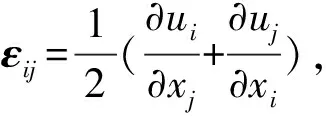
物理方程σij=λδijεkk+2μεij，

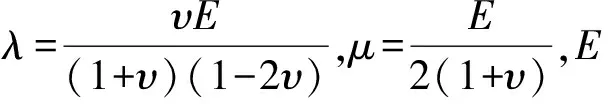
流體施加于結構上的動壓力載荷分量ki為

式中：n為邊界的法向方向矢量。

2 靜壓軸承流固耦合建模

2.1 幾何模型簡化

靜壓軸承結構簡圖如圖1所示，在建立流固耦合計算模型的過程中，需要對模型進行相應的簡化處理[3]，以減小工作量，同時還能夠準確地模擬出靜壓軸承真實的工作狀態。

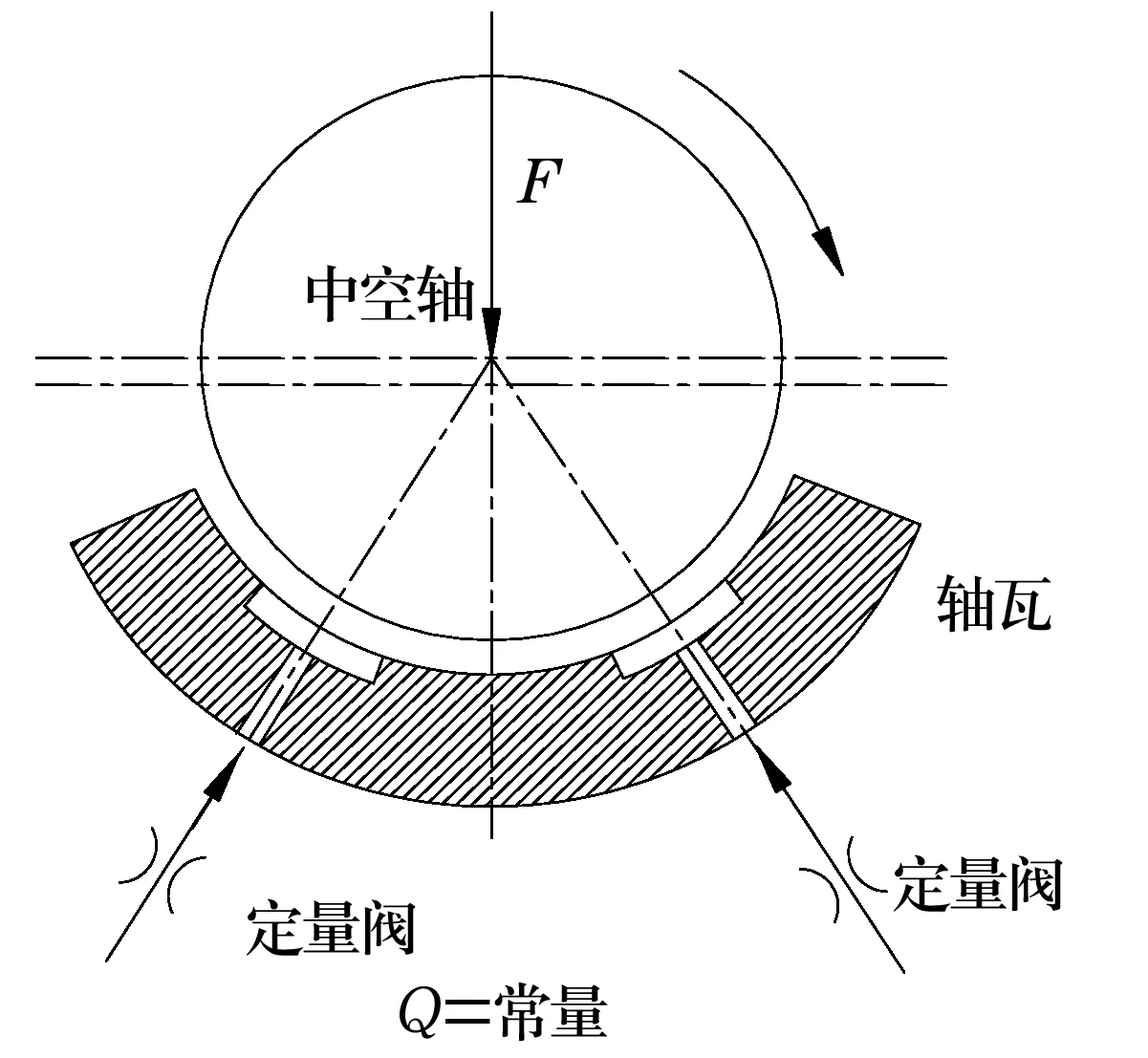
圖1 靜壓軸承簡圖

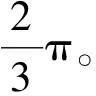
2.2 網格劃分

使用ANSYS Workbench軟件分別對靜壓軸承的中空軸與軸瓦進行六面體網格劃分(圖2)。使用ANSYS ICEM CFD 軟件對靜壓軸承的油膜進行六面體網格劃分(圖3)。同時，為保證計算精度，在油膜的厚度方向布置 5 層網格。

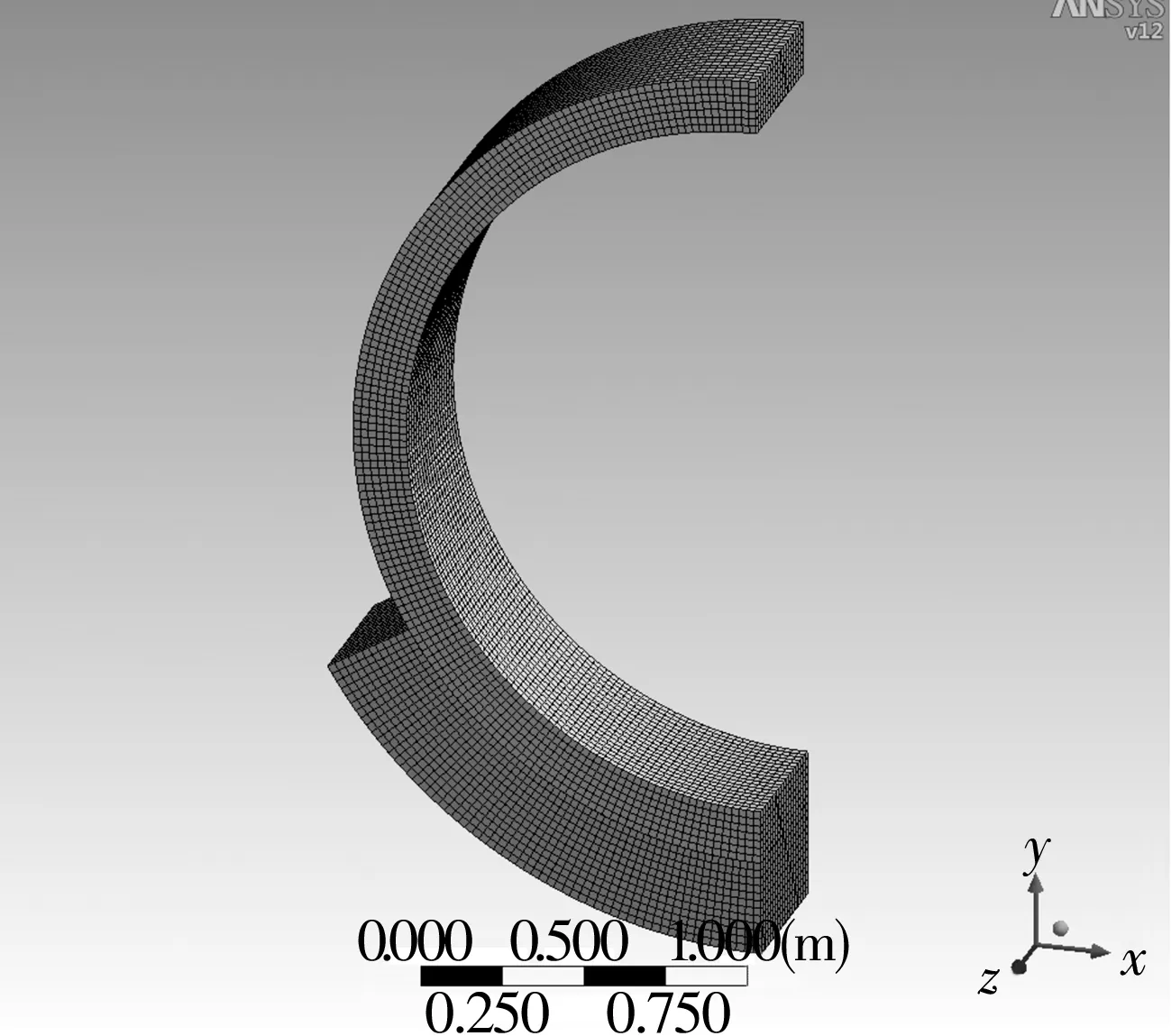
圖2 中空軸與軸瓦網格

圖3 油膜網格

2.3 物理模型與邊界條件設置

中空軸材料為鑄鋼ZG20SiMn，其彈性模量為210 GPa，泊松比為0.3，屈服強度為295 MPa。軸瓦材料為鋁青銅ZCuAl10Fe3Mn2，彈性模量為135 GPa，泊松比為0.27，許用壓強為20 MPa。根據靜壓軸承設計條件，采用N220潤滑油，油腔油壓為3.37 MPa，一端軸承的等效載荷為1 960 kN。Workbench 結構區域模型如圖4所示，CFX 流體區域模型如圖5所示。

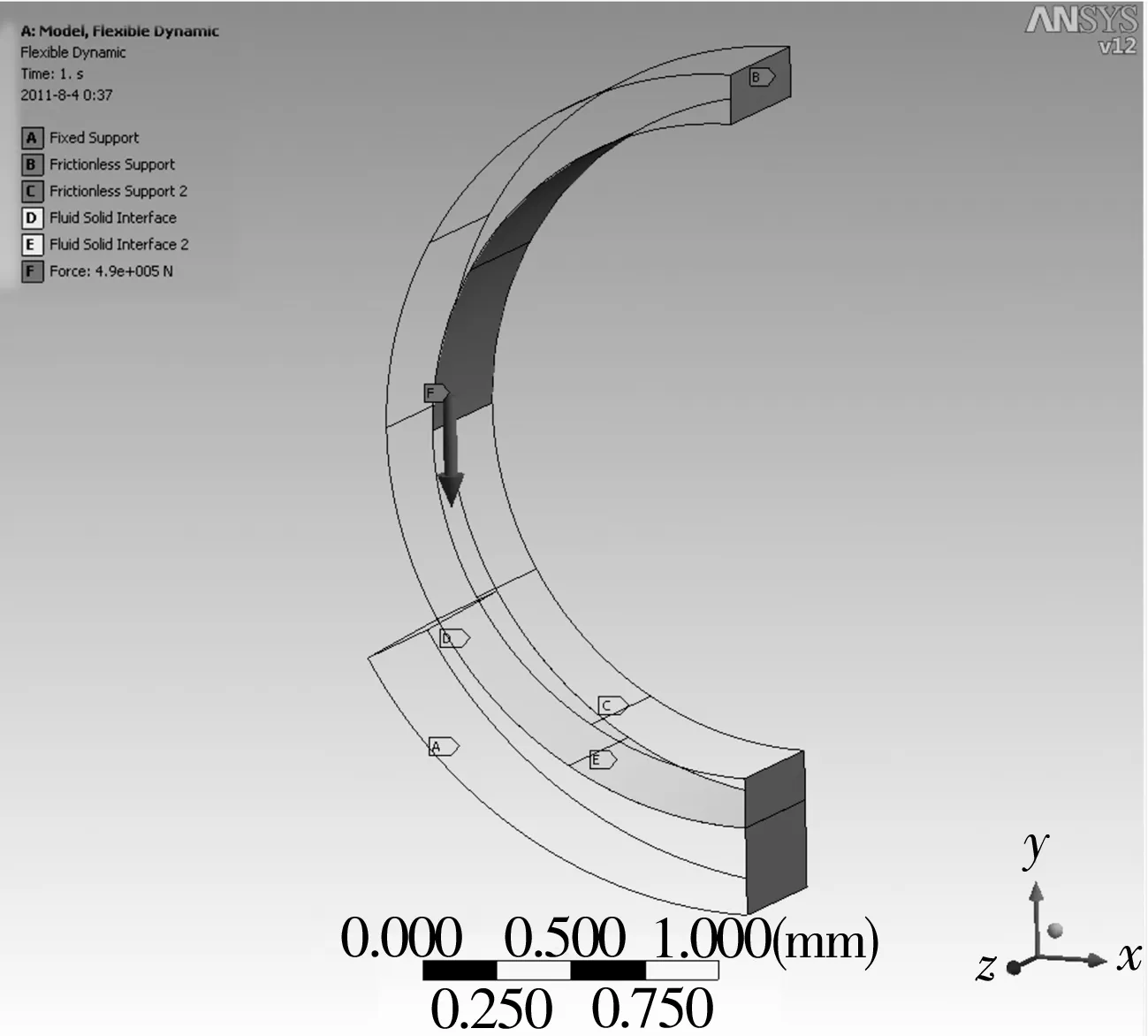
圖4 Workbench模型

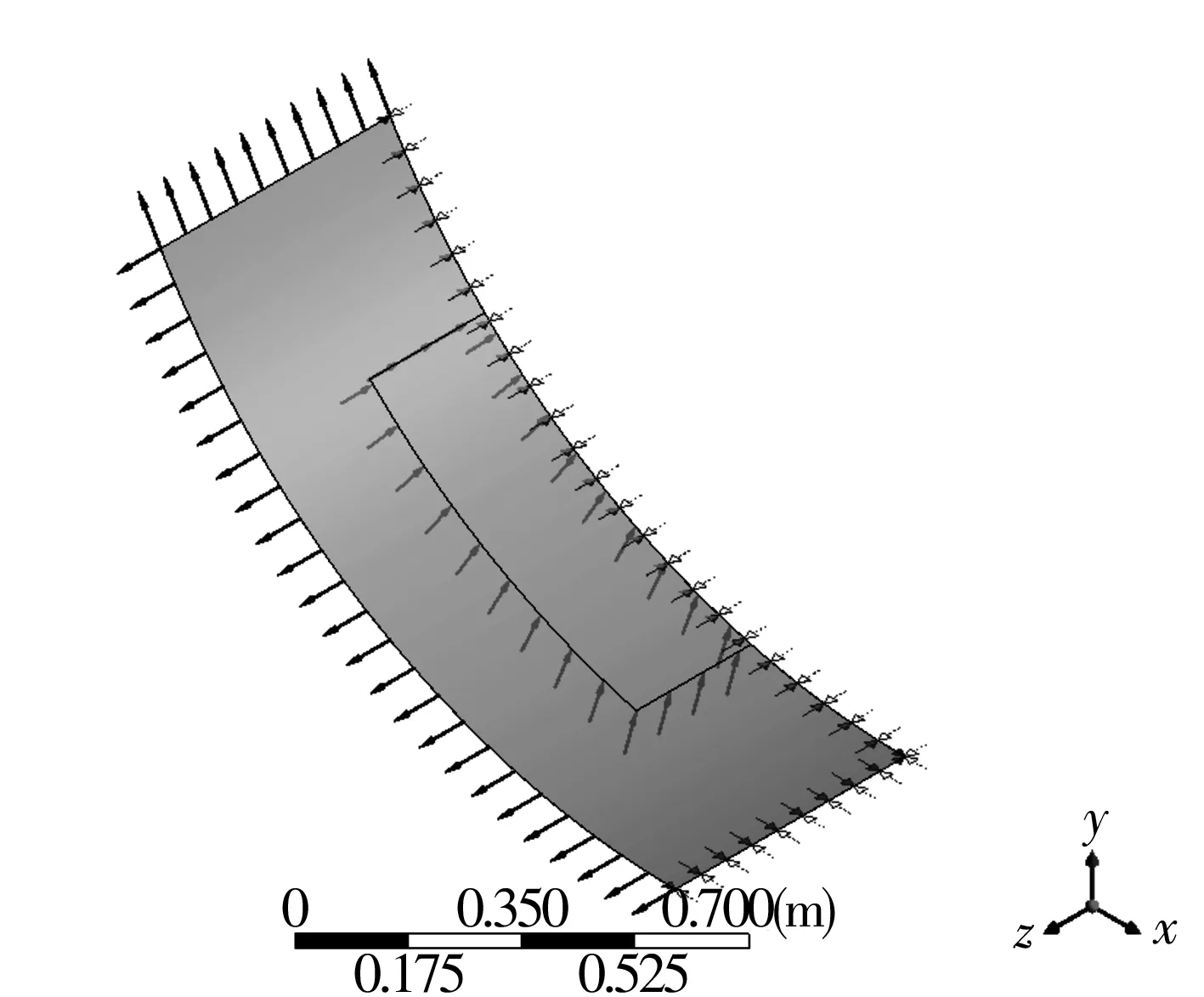
圖5 CFX模型

2.4 流固耦合計算結果

圖6為結構所受應力情況，可看出中空軸受力較大，所受最大應力為46.69 MPa；流固耦合計算達到平衡后，由于靜壓軸承油膜的承載能力將中空軸浮升，使中空軸能夠有效承載。

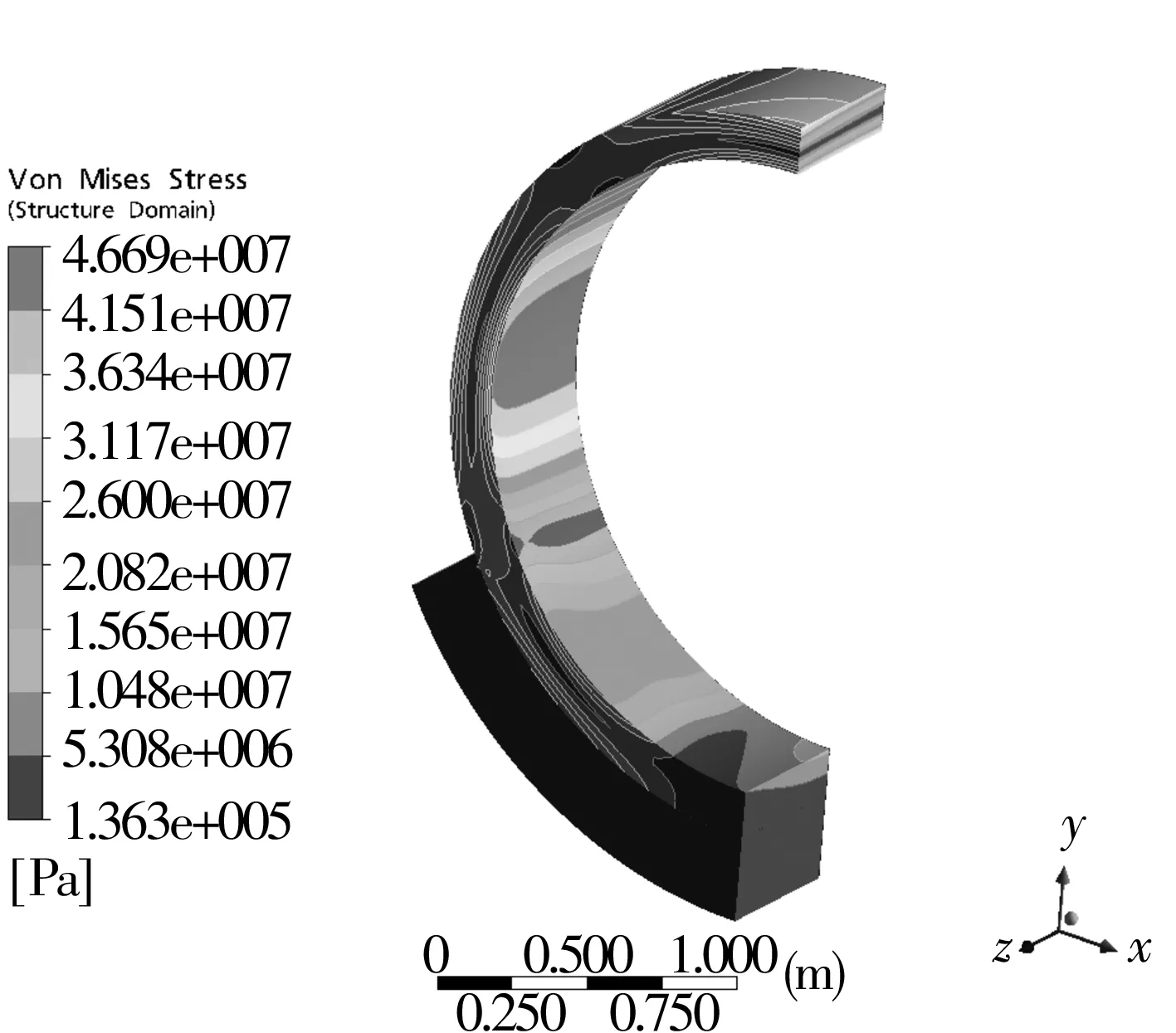
圖6 結構所受應力情況

圖7為油膜表面壓力分布情況，可以看到油膜油腔附近區域壓力較大，最大油壓為3.435 MPa；流固耦合計算達到平衡后，油膜內部能形成良好的壓力分布，從而使油膜具有足夠的剛度和承載能力。

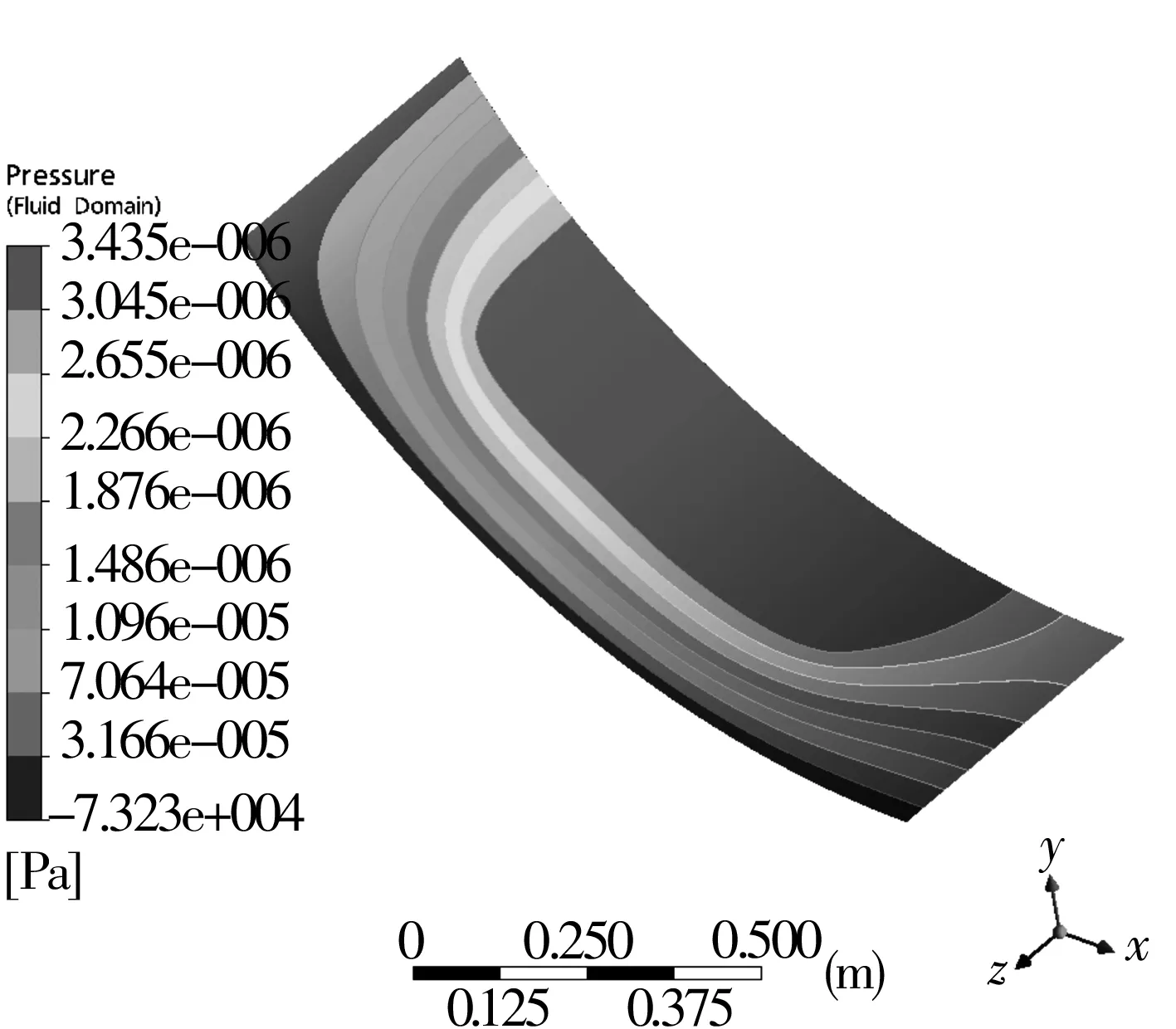
圖7 油膜表面壓力分布情況

圖8為中空軸流固耦合交界面應力分布情況，由于油膜的承載作用以及油膜油腔附近區域壓力較大，使中空軸流固耦合交界面與油膜油腔對應位置的受力較大，進而導致應力集中，最大應力為28.1 MPa。

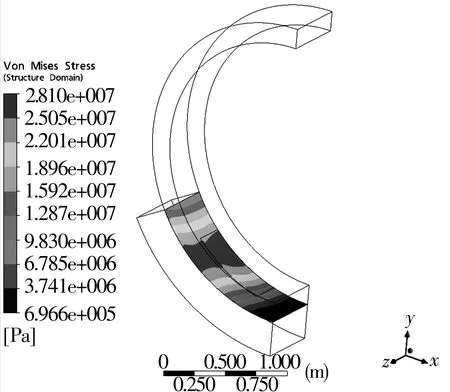
圖8 中空軸流固耦合交界面應力

圖9為軸瓦流固耦合交接面應力分布情況，由于軸瓦對中空軸的支撐形成簡支效果，導致軸瓦流固耦合交界面上軸瓦端部形成應力集中，最大應力為3.37 MPa。

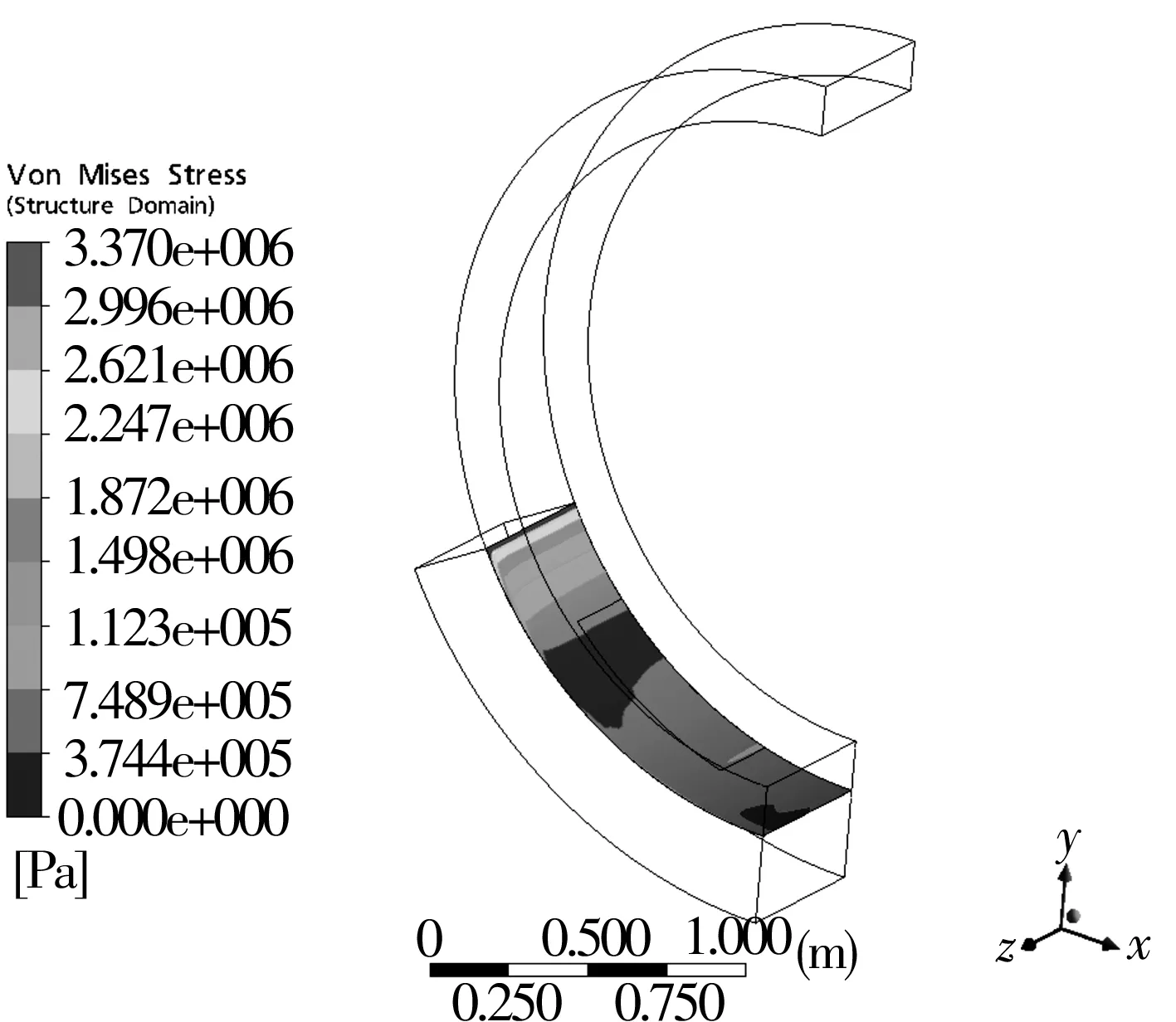
圖9 軸瓦流固耦合交接面應力

圖10為中空軸流固耦合交界面變形情況，可以看到中空軸流固耦合交界面與軸瓦端部對應位置的變形最大，最大變形量為0.430 5 mm。

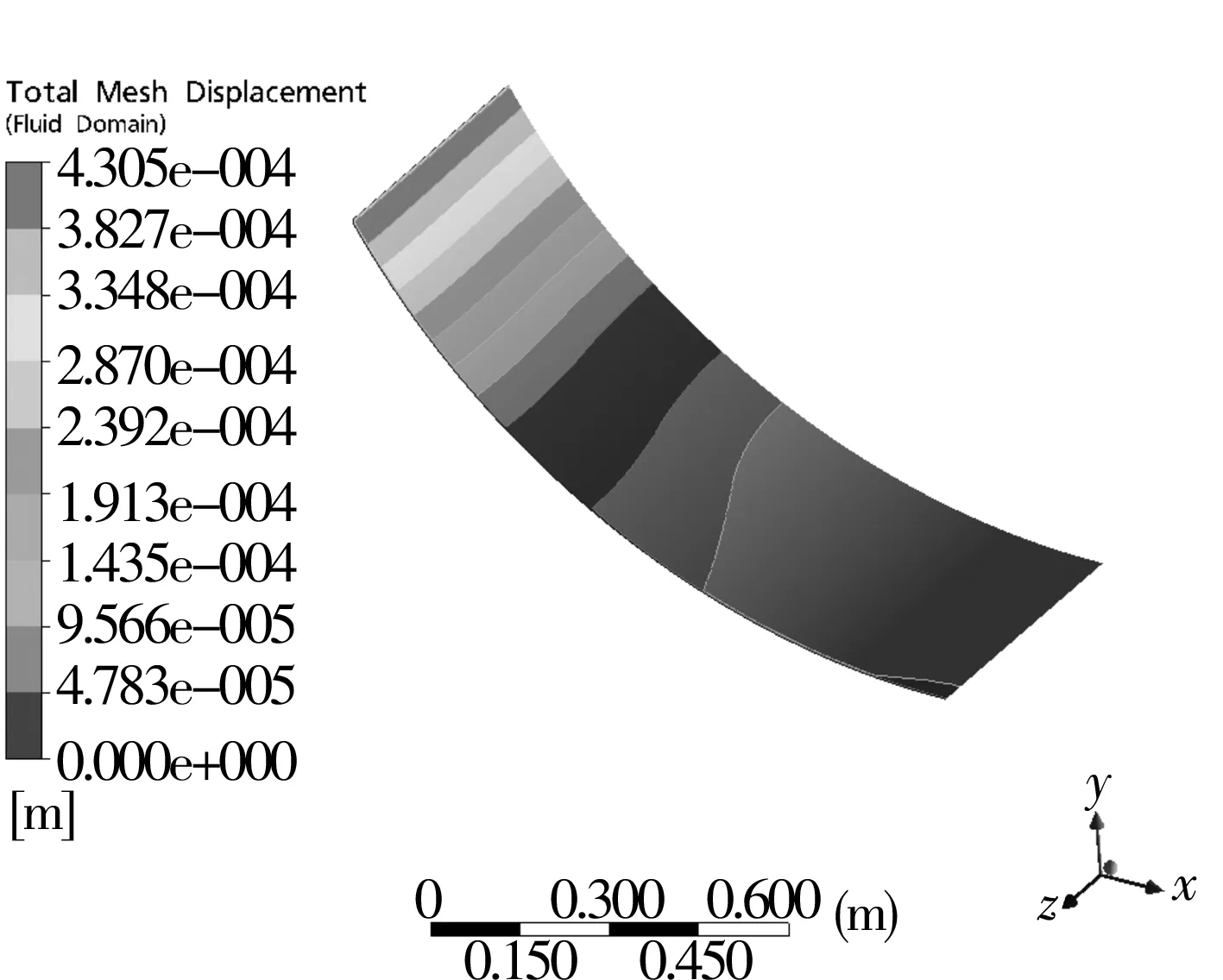
圖10 中空軸流固耦合交界面變形

圖11為軸瓦流固耦合交界面變形情況，可以看到軸瓦流固耦合交界面上軸瓦端部位置的變形最大，最大變形量為0.430 2 mm。對比中空軸流固耦合交界面(對應油膜上表面)與軸瓦流固耦合交界面(對應油膜下表面)的變形情況，可以看到承載時油膜產生的變形極其微小，即載荷對油膜的厚度影響較小，說明油膜具有足夠的剛度和承載能力。

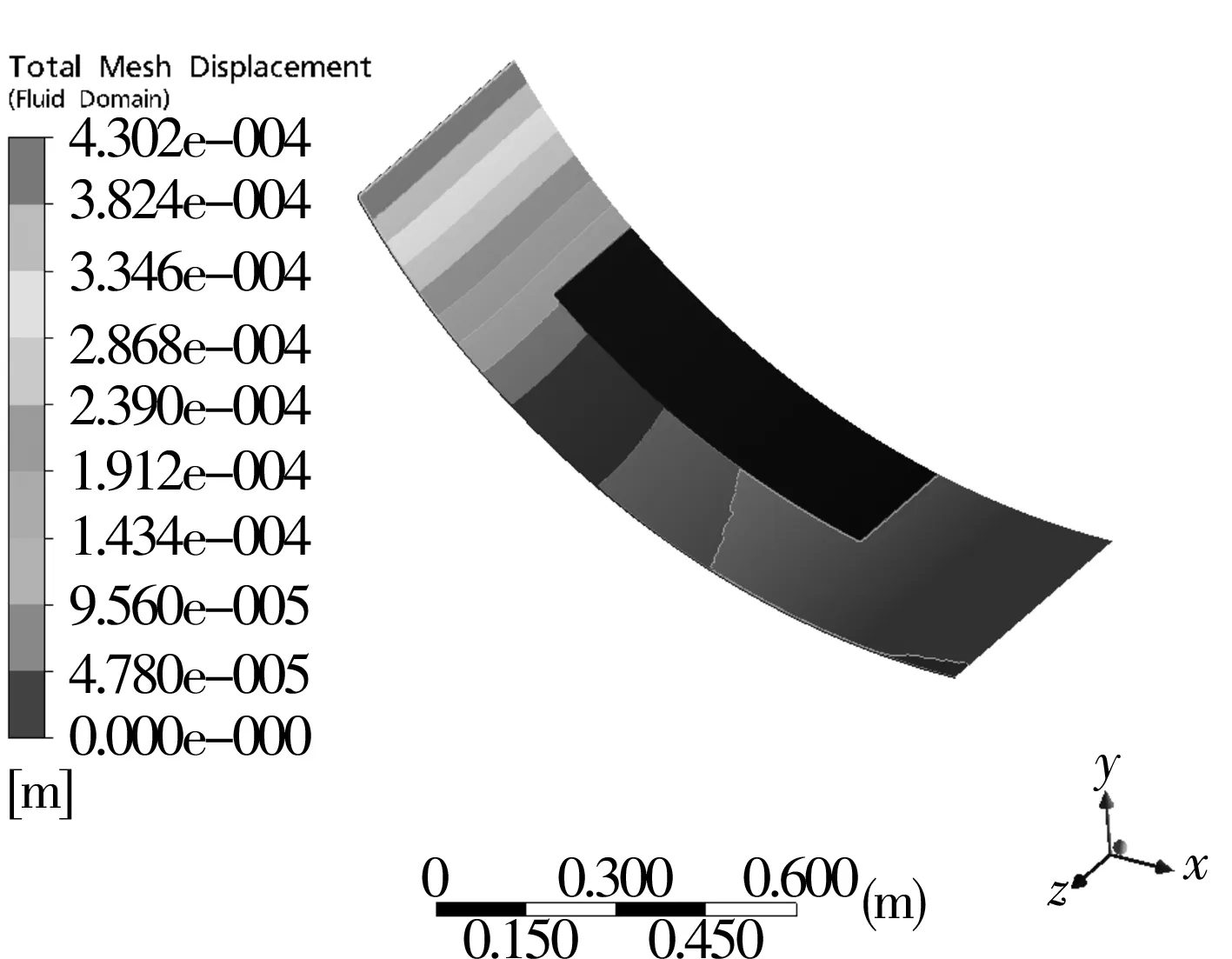
圖11 軸瓦流固耦合交界面變形

3 結論

通過流固耦合分析計算，中空軸所受最大應力為46.69 MPa，遠小于其材料的屈服極限；軸瓦應力最大值為3.37 MPa，遠小于軸瓦材料的許用壓強值；靜壓軸承在承載時油膜厚度的變化極其微小，說明油膜具有足夠的承載能力，不會出現承載時油膜破壞使中空軸與軸瓦接觸(即燒瓦)的情況。因此，該靜壓軸承的油膜承載能力和材料的結構強度均符合設計要求。