基于ANSYS的卡輪軸承外圈斷裂原因分析

張鋼，李明彥，王慶祥，白華，阮娟

(1．上海大學 機電工程與自動化學院，上海 200072；2．優必勝(上海)精密軸承制造有限公司，上海 200444)

燒結機臺車卡輪是臺車中的關鍵部件，傳統的滑動軸承卡輪結構存在各種弊端；滿裝圓柱滾子軸承徑向承載能力大，結構形式多，加工技術成熟，是替代傳統滑動軸承卡輪的最佳選擇[1]。但是外圈作為卡輪的直接承載部件，在高溫重載并伴隨有沖擊的工況下極易出現斷裂。在卡輪軸承的材料和熱處理等加工質量均符合技術要求的前提下，分析卡輪軸承零件上的應力對尋找卡輪軸承外圈斷裂原因具有重要的意義[2]。

基于Hertz彈性接觸理論的計算方法由于采用了半無限空間的邊界條件和剛性套圈的假設，僅適用于簡單形狀物體的分析，難以滿足復雜結構和復雜載荷下軸承性能分析的精度要求。有限元法能建立更符合實際結構和邊界條件的模型，其計算結果與試驗結果更為接近[3-9]。

文中采用ANSYS有限元分析軟件建立卡輪軸承受載最大滾子與套圈的接觸模型和外圈簡化梁模型，以分析卡輪軸承外圈斷裂的原因。

1 受載最大滾子與套圈的接觸分析

文中涉及的卡輪軸承是雙列滿裝圓柱滾子軸承，外徑為250 mm，內徑為160 mm，外滾道直徑為219.5 mm，內滾道直徑為183.5 mm，每列35粒滾子，滾子直徑為18 mm，滾子有效長度為42 mm，徑向載荷為939.68 kN。

接觸問題的求解是一種高度非線性過程，需要較多的計算資源，為進行更為有效便捷的計算，理解問題的特征并建立合理的模型是很重要的。卡輪軸承尺寸大，滾子數目多，若建立整體軸承的三維模型進行分析，粗糙的網格使得求解誤差極大；而高質量網格單元多、計算量大甚至計算無法進行，并且接觸對多且設置復雜，稍有偏差就會引起不收斂。為了對卡輪軸承進行準確的分析，取受載最大滾子為研究對象，考慮到對稱性，建立單個滾子與對應套圈的四分之一模型進行分析。

1.1 有限元模型的建立

建模時長度單位選擇m，應力單位為Pa，集中力單位為N。采用的單元類型為Solid 8node185，軸承材料為GCr15鋼，其密度為7 800 kg/m3，彈性模量E=206 GPa，泊松比μ=0.3。為防止滾子端部應力集中，實體建模時滾子軸向有效長度比內、外套圈寬度稍短一點，用智能一級分網方式進行網格劃分，可以自動對接觸部位的網格進行細化，實體模型和有限元模型如圖1所示。

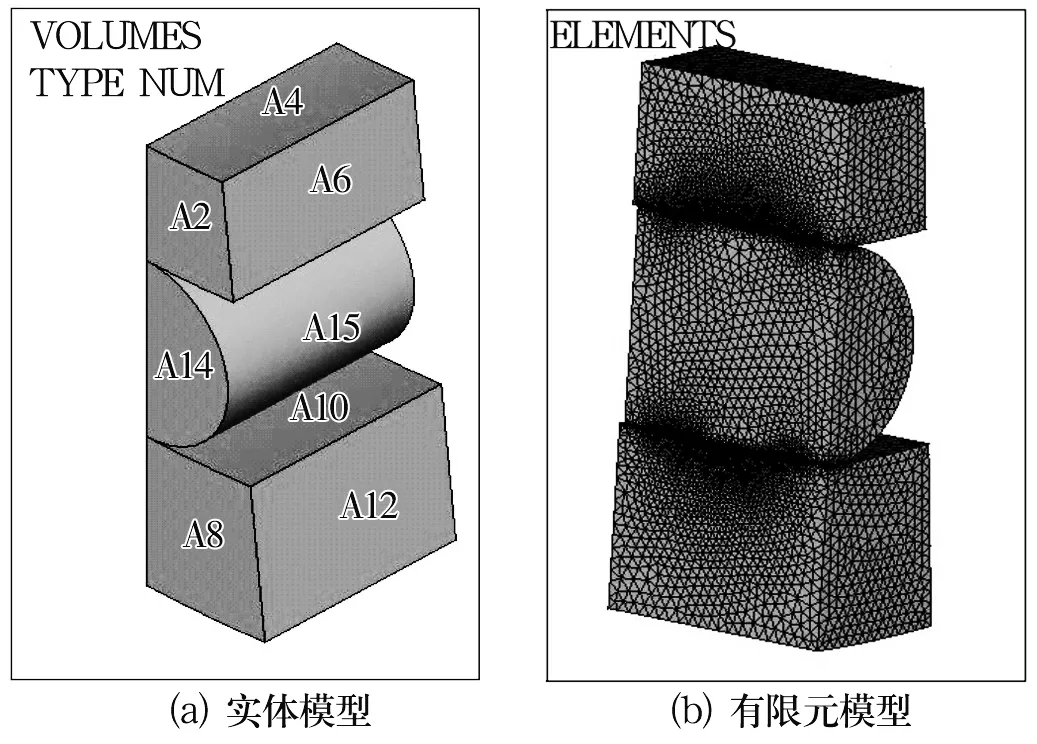
圖1 單個滾子與套圈接觸的1/4模型

1.2 創建接觸對并設置接觸參數

接觸類型的選擇和接觸對的設置直接關系到求解計算的收斂性。卡輪軸承滾子與套圈相互作用的過程中都會產生一定的變形，因此采用柔-柔接觸方式，面-面接觸類型，在接觸管理器中設置接觸對，選擇滾子面為目標面，內、外套圈滾道面為接觸面，創建兩個3D面面接觸對。采用增廣Lagrange算法，為保證收斂性，設置實常數FKN(接觸剛度)為0.2，FTOLN(最大滲透范圍)為0.1。

1.3 定義邊界條件、施加載荷并求解

卡輪軸承內圈與車軸過盈配合，運轉過程中保持靜止，外圈旋轉并承受載荷，因此邊界條件定義為：內圈內圓面全固定約束，1/4模型截面對稱約束，外圈外圓面施加載荷。受載最大滾子承受的載荷為109.54 kN。選擇靜態分析類型，設定求解時間為1，子步數為100，最小子步數為20，最大子步數為1 000，打開自動時間步長。在非線性對話框中將Line search項置為on，DOF solution predictor項置為On for all substp。對模型進行非線性分析，計算結果收斂。

1.4 求解結果

ANSYS中用應力等值線來表示模型內部應力分布情況，分析得到的各方向應力分布如圖2所示。

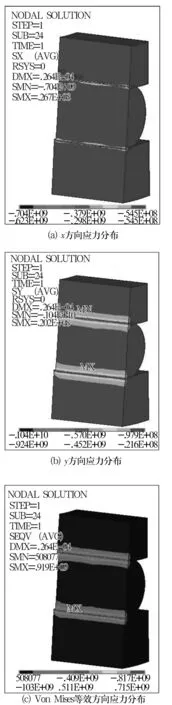
圖2 滾子與套圈上的應力分布云圖

x方向最大應力σxmax=704 MPa；y方向最大應力σymax=1 040 MPa；Von Mises最大等效應力σvmmax=919 MPa。σvmmax超過了材料的屈服極限σs=412 MPa，會產生大的塑性變形。y方向最大應力σymax和Von Mises最大等效應力σvmmax甚至超過了材料的抗拉強度極限σb=716 MPa，說明軸承強度不夠，極易引起斷裂失效。由圖2還可以看到，最大應力發生在滾子與內圈接觸部位，但是卡輪軸承是外圈先發生斷裂。這主要是因為外力直接作用在外圈局部，不確定的沖擊作用下，外圈強度不夠則最易發生斷裂，但外力要經過滾子的傳遞才到達內圈，并且軸承內部填充的潤滑脂對載荷傳遞給內圈也產生了一定的延遲效應，減緩了力的作用時間，使得內圈受力穩定而均勻，降低了內圈斷裂的可能性。

由于卡輪軸承是外圈發生斷裂，為此把外圈單獨分離出來，重點分析外圈上的應力分布情況，如圖3所示。

可以看到外圈上σxmax，σymax，σvmmax分別為693，888和463 MPa，σvmmax大于材料的屈服極限σs，外圈會產生大的塑性變形，y方向最大應力超過材料的抗拉強度極限σb，外圈強度不夠容易引起斷裂。

Hertz接觸理論可以很好地定義軸承的接觸，接觸應力理論值與有限元分析值之間的對比可以驗證有限元分析結果的有效性。因此，選取接觸應力為顯示對象，其具體分布如圖4所示。

圖4a是把模型對稱擴展為整個滾子時的接觸應力分布情況，結合圖4b和圖4c可以看出，由ANSYS分析得到的接觸應力分布以及接觸面形狀與Hertz接觸理論所闡述的線接觸狀況完全相同：載荷作用下，表面接觸應力呈拋物線分布，在拋物線的頂點達到最大，兩端逐漸減小為零；接觸面形狀是較小寬度范圍內的矩形。接觸應力Hertz理論值與ANSYS分析值的對比見表1。

表1 接觸應力值比較 MPa

經過對比可知：ANSYS分析值與Hertz理論值比較吻合，誤差不超過5%；并且有限元分析得到的最大接觸應力發生在滾子與內圈滾道接觸處，與理論結果相符，證明了有限元分析的正確性與有效性。

2 外圈簡化模型的線性靜力分析

套圈在承受滾子壓力作用時，局部的變形相當于彈性基礎上的梁。卡輪軸承承受的是單一線載荷，在外載荷作用的瞬間，外圈受載部位可認為是兩個滾子為支點的簡支梁。因此，從外圈簡化梁模型的角度出發對其進行有限元分析。

2.1 外圈簡支梁有限元模型的建立

簡支梁模型的有限元分析是簡單的結構線性靜力分析，遵循ANSYS分析的一般過程。

選擇面單元Solid 4node 42和體單元Solid8node185，材料屬性與前述接觸分析相同，由ANSYS內部自低向上的建模方法建立實體模型，設定模型邊線單元大小為0.000 2，先對扇形截面進行Map分網，再通過掃略方式得到體網格，如此劃分的網格規范整齊，最后得到外圈簡支梁有限元模型如圖5所示。

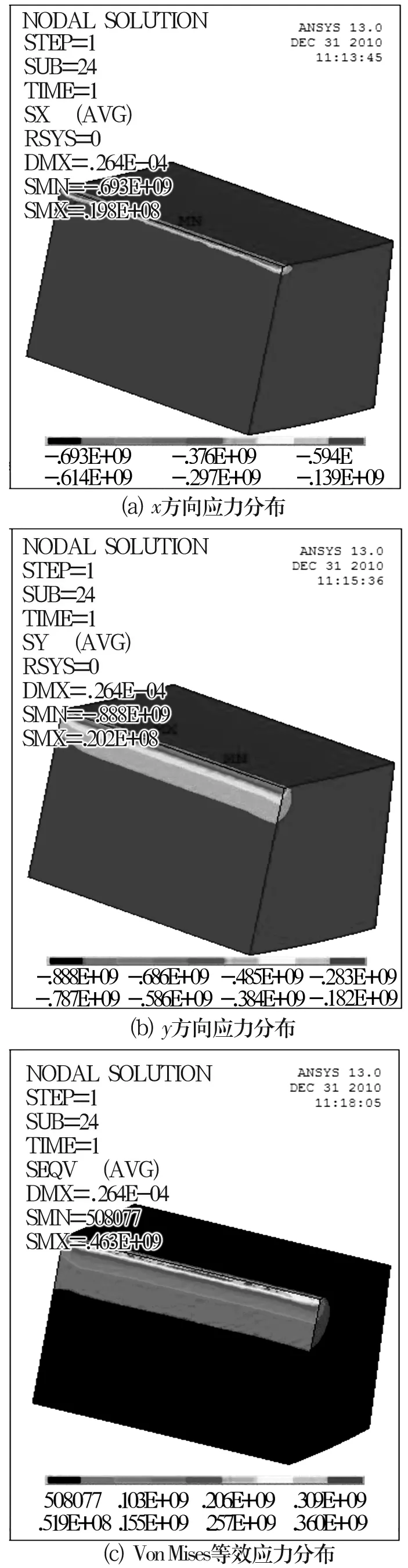
圖3 外圈上的應力分布云圖

2.2 定義邊界條件、施加載荷并求解

對兩個扇形端面全約束，凹形截面x，z向約束。徑向外載荷為939.68 kN，為了最大程度地模擬卡輪軸承真實的受載狀況，在滾道的兩條邊線施加向下的線載荷，外圈外圓面的中間部位施加向上的面載荷，選擇靜態分析類型，完成求解。

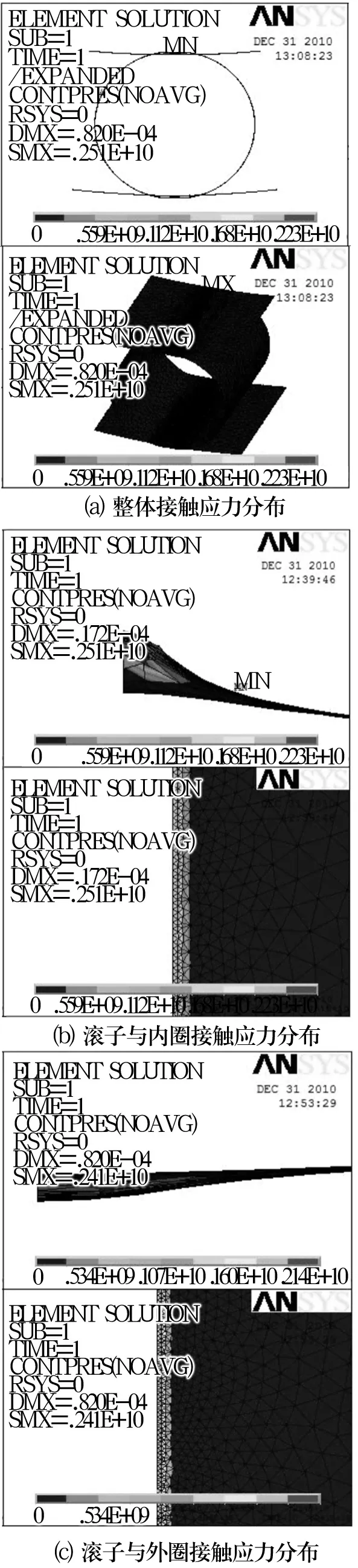
圖4 接觸應力分布云圖

圖5 外圈簡支梁有限元模型

2.3 梁模型的求解結果

外圈梁結構上各應力的分布如圖6所示。分析得到外圈簡支梁上各個方向的最大應力分別為σxmax=495.867 MPa，σymax=986.679MPa，σvmmax=820.567 MPa；而根據彈性梁的彎曲變形理論，計算得到的外圈梁上最大彎曲應力為865.8 MPa。有限元分析得到的最大等效應力σvmmax與該理論值相差不多，再次證明了有限元分析的準確性。同時，還可以看到：這些最大應力都超過了GCr15軸承鋼的屈服極限σs，y方向最大應力和最大等效應力超過了材料的抗拉強度極限σb，外圈不但會發生大的塑性變形，而且極易出現斷裂。

圖6 外圈簡支梁模型應力云圖

3 結束語

卡輪軸承接觸模型和外圈簡支梁模型的有限元分析結果與對應的理論分析結果之間的吻合度極高，并且兩者的分析結論一致，證明了有限元分析結果的有效性和正確性。

卡輪軸承外圈上各方向的最大應力都超過了GCr15鋼的屈服極限σs，有的甚至超過材料抗拉強度極限σb，軸承強度不夠，不但會發生塑性變形，而且在沖擊重載作用下，極易發生斷裂失效。卡輪軸承在結構設計和材料選擇上可以通過增大外圈壁厚、選用強度更高的材料來改善軸承性能。所以，對于這種低速重載軸承，只按照傳統理論中由基本額定靜載荷和基本額定動載荷進行設計校核計算，是不能滿足軸承的實際使用條件的，還必須要校核套圈的彎曲強度。

ANSYS有限元分析可以得到軸承零件上的應力分布情況，能夠快速地確定模型中的最危險區域，可以替代傳統的理論分析，為判斷軸承的失效形式提供一定的參考依據。