支持媒體處理的子字絕對(duì)值單元設(shè)計(jì)與實(shí)現(xiàn)*
開耀文,高德遠(yuǎn),張 萌
(西北工業(yè)大學(xué)計(jì)算機(jī)學(xué)院,西安710129)
1 前言
當(dāng)前,為了滿足多媒體應(yīng)用的需要,很多通用處理器提供了針對(duì)多媒體應(yīng)用的擴(kuò)展指令。如Intel的MMX,AMD 的3DNow!,以及 Motorola的 AltiVec等。
多媒體應(yīng)用具有兩個(gè)基本特點(diǎn):數(shù)據(jù)并行度高和數(shù)據(jù)精度要求低[1]。子字并行技術(shù)是一種單指令流多數(shù)據(jù)流技術(shù),它的原理是一條指令中的數(shù)據(jù)可以拆分成多個(gè)子字并行執(zhí)行。例如AltiVec指令集中,參與計(jì)算的操作數(shù)位數(shù)為128位,這些操作數(shù)可以選擇4個(gè)32位字的,或者8個(gè)16位半字,或者16個(gè)8位字節(jié)進(jìn)行運(yùn)算。子字并行運(yùn)算的特點(diǎn)正好與多媒體應(yīng)用的特點(diǎn)相符合,是一種有效提高多媒體應(yīng)用性能的手段。
在圖像處理中,兩個(gè)數(shù)的絕對(duì)值運(yùn)算|A-B|得到了廣泛應(yīng)用,例如視頻中的運(yùn)動(dòng)估計(jì)和預(yù)測(cè)算法中就采用了大量的這種絕對(duì)值運(yùn)算。在沒(méi)有實(shí)現(xiàn)絕對(duì)值單元的通用處理器中,實(shí)現(xiàn)一個(gè)無(wú)符號(hào)絕對(duì)值運(yùn)算需要進(jìn)行A-B和B-A運(yùn)算,并將結(jié)果相或,實(shí)現(xiàn)一個(gè)有符號(hào)絕對(duì)值運(yùn)算則需要更復(fù)雜的步驟。而采用了絕對(duì)值單元的處理器只需要一條指令就能實(shí)現(xiàn)通用處理器中需要多條指令實(shí)現(xiàn)的絕對(duì)值運(yùn)算。絕對(duì)值單元在減少計(jì)算指令數(shù)的同時(shí)減少了訪存次數(shù),因?yàn)榻^對(duì)值運(yùn)算只需要一次取出操作數(shù)做運(yùn)算,而不用像通用處理器那樣需要多次取數(shù)。絕對(duì)值運(yùn)算是建立在普通減法運(yùn)算基礎(chǔ)上的,通過(guò)擴(kuò)展原有加法器實(shí)現(xiàn)絕對(duì)值單元可以使普通的加法器與絕對(duì)值單元共享一個(gè)計(jì)算單元,這樣實(shí)現(xiàn)絕對(duì)值單元的代價(jià)是較小的。
2 并行前綴加法器原理
2.1 加法器原理
考慮加法器的進(jìn)位傳播公式[2]:


單個(gè)進(jìn)位生成和not kill信號(hào)給出如下:

公式(1)和(2)的信號(hào)可以概括地描述為:在多位組所包括的位z...x范圍內(nèi),可分成高位組和低位組兩個(gè)子組,進(jìn)位生成信號(hào)是由兩方面決定的:高位子組z….y生成進(jìn)位信號(hào)或者低位子組y-1...x生成進(jìn)位,而低位子組的生成進(jìn)位信號(hào)不被“殺死”。如果高位子組和低位子組的都不“殺死”進(jìn)位,那么這個(gè)組也不“殺死”進(jìn)位。
公式3說(shuō)明第i位的進(jìn)位信號(hào)即是第i-1位到第0位的組進(jìn)位生成信號(hào)。根據(jù)求和公式Si=Pi8 ci可得到A與B的和,其中Pi為單個(gè)位的進(jìn)位傳播信號(hào),Pi=Ai8Bi;Si為和的第i位。
因此,加法可以縮減為三步來(lái)進(jìn)行[3]:
(1)使用公式4和5按位計(jì)算進(jìn)位生成和not kill信號(hào);
(3)結(jié)合公式3和求和公式計(jì)算求和信號(hào)。
顯然,進(jìn)位生成邏輯是整個(gè)計(jì)算的關(guān)鍵。加法器運(yùn)算的優(yōu)化核心就是減小進(jìn)位信號(hào)的生成時(shí)間。由此引出了各種優(yōu)秀的加法器設(shè)計(jì),如超前進(jìn)位加法器,條件加法器,旁路進(jìn)位加法器和并行前綴加法器。其中,相對(duì)于其它加法器結(jié)構(gòu),并行前綴加法器對(duì)于位寬較大的加法運(yùn)算(N>16)可以較好的控制延時(shí)增長(zhǎng),通過(guò)構(gòu)造多級(jí)結(jié)構(gòu)可以取得以logN增長(zhǎng)的延時(shí)[3]。通過(guò)構(gòu)造并行前綴樹,快速的計(jì)算出各個(gè)位的進(jìn)位信號(hào),從而快速計(jì)算出加法結(jié)果。
2.2 并行前綴樹原理
1.并行前綴計(jì)算公式如下[4]:
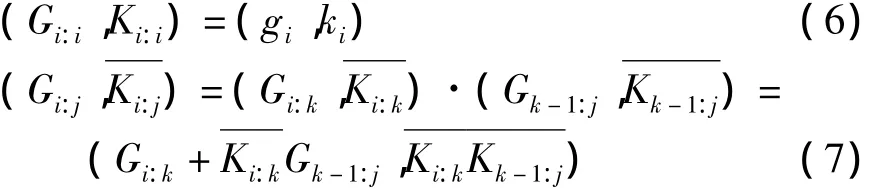
式中,“·”算符為前綴計(jì)算算符。前綴計(jì)算算符具有兩個(gè)重要的計(jì)算性質(zhì):結(jié)合律及冪等律,即滿足以下公式:

結(jié)合律使得整個(gè)計(jì)算式可以并行計(jì)算,冪等律允許各并行計(jì)算子項(xiàng)交疊執(zhí)行,從而給并行前綴加法器的構(gòu)造帶來(lái)很大的靈活性[5]。不同的并行前綴加法器正是對(duì)并行子項(xiàng)的不同區(qū)間運(yùn)用了結(jié)合律和冪等率而得到的。圖1給出了ladner-Fischer[6]的并行前綴樹示意圖,圖中黑點(diǎn)采用公式1和2,灰點(diǎn)采用公式1。ladner-Fischer樹的構(gòu)造較為簡(jiǎn)單,各個(gè)計(jì)算子項(xiàng)沒(méi)有重疊,計(jì)算層數(shù)達(dá)到最優(yōu)。
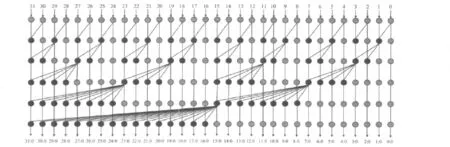
圖1 32位ladner-Fischer加法器并行前綴樹示意圖
3 絕對(duì)值運(yùn)算的研究與設(shè)計(jì)
通常,計(jì)算絕對(duì)值的方法是將兩個(gè)數(shù)大小進(jìn)行比較,再根據(jù)比較的結(jié)果,用大值減去小值,或者直接計(jì)算兩個(gè)數(shù)的減法,再對(duì)結(jié)果取正值。硬件實(shí)現(xiàn)中[7],這種計(jì)算方法需要兩步運(yùn)算。顯然,兩步運(yùn)算增加了關(guān)鍵路徑的長(zhǎng)度,從而對(duì)整個(gè)運(yùn)算的時(shí)序產(chǎn)生影響。為了消除這樣的兩步運(yùn)算,可以通過(guò)另外一種方法解決[8]。這種方法的思想基于條件加法器,即同時(shí)計(jì)算A-B和B-A,通過(guò)計(jì)算結(jié)果的符號(hào)位選擇結(jié)果為正數(shù)的計(jì)算通路。
然而,這種方法在減小關(guān)鍵路徑的同時(shí),大大增加了計(jì)算單元的面積,因?yàn)樗肓藘蓷l計(jì)算通路。
3.1 絕對(duì)值運(yùn)算的分析
通過(guò)觀察發(fā)現(xiàn),無(wú)論用何種方法,絕對(duì)值運(yùn)算中,兩個(gè)數(shù)的減法運(yùn)算是必須的過(guò)程。同其它運(yùn)算一樣,絕對(duì)值運(yùn)算的操作數(shù)也分有符號(hào)數(shù)和無(wú)符號(hào)數(shù),以下分別通過(guò)有符號(hào)操作數(shù)和無(wú)符號(hào)操作數(shù)來(lái)分析絕對(duì)值運(yùn)算。
3.1.1 有符號(hào)絕對(duì)值運(yùn)算
對(duì)于有符號(hào)數(shù),補(bǔ)碼的加減法運(yùn)算是最常見的運(yùn)算方法,因?yàn)橛蟹?hào)數(shù)補(bǔ)碼減法可以轉(zhuǎn)化為有符號(hào)數(shù)補(bǔ)碼加法的運(yùn)算,所以這里討論的都是基于補(bǔ)碼的運(yùn)算法則,并且參與運(yùn)算的兩個(gè)數(shù)都為有符號(hào)數(shù)。約定A為A的所有位取反。A-B=A+(B+1),B=-(B+1),在加法運(yùn)算前將B的所有位取反得到的結(jié)果為A-B-1。如果這個(gè)值是正數(shù),加法器的結(jié)果加1就是絕對(duì)值的計(jì)算結(jié)果。反之,如果加法器的結(jié)果是負(fù)數(shù),將加法器結(jié)果的所有位取反得到的結(jié)果為-(A-B-1+1)=B-A,也為絕對(duì)值的結(jié)果。所以,絕對(duì)值運(yùn)算可以實(shí)現(xiàn)為在加法器中加入兩個(gè)控制信號(hào):和加一信號(hào)inc和取反信號(hào)inv,并且其中一個(gè)操作數(shù)在送入加法器中時(shí)全部取反。顯然,inc=inv。如果加法器結(jié)果的符號(hào)位為負(fù),則將加法器結(jié)果的全部位取反即可。如果加法器結(jié)果的符號(hào)位為正,則還要對(duì)加法器的結(jié)果加1。
3.1.2 無(wú)符號(hào)絕對(duì)值運(yùn)算
兩個(gè)有n個(gè)數(shù)字的二進(jìn)制無(wú)符號(hào)絕對(duì)值|M-N|可按以下步驟進(jìn)行:
(1)將被減數(shù)M與減數(shù)N的補(bǔ)碼相加,即:
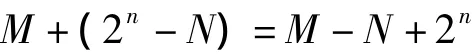
(2)當(dāng)M>=N,M-N的值即為絕對(duì)值的大小。觀察發(fā)現(xiàn),如果M>=N時(shí),結(jié)果將產(chǎn)生進(jìn)位2n,舍去這個(gè)進(jìn)位,得到的就是M-N。
(3)當(dāng)M<N,那么N-M的值即為絕對(duì)值的大小,對(duì)于這種情況,將被減數(shù)M與減數(shù)N的反碼相加,即:
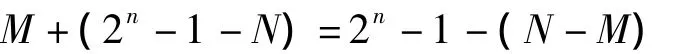
由于N>M,結(jié)果和不會(huì)產(chǎn)生進(jìn)位,且為N-M的反碼,將結(jié)果取反即可得到N-M的值。通過(guò)以上分析可知,無(wú)符號(hào)絕對(duì)值運(yùn)算與有符號(hào)絕對(duì)值運(yùn)算具有共同的性質(zhì),總結(jié)如下:
·兩操作數(shù)之一需要求反送入加法樹中,即進(jìn)行減法運(yùn)算;
·對(duì)加法樹出來(lái)的結(jié)果位處理方式相同,取反或者結(jié)果加1。
顯然,取反運(yùn)算相對(duì)于結(jié)果加1運(yùn)算的延時(shí)小很多。所以,結(jié)果加1處于關(guān)鍵路徑上。最壞情況下,加1運(yùn)算的進(jìn)位傳播延時(shí)經(jīng)過(guò)加法器結(jié)果的每一位,這對(duì)于整個(gè)計(jì)算單元時(shí)序的影響是很大的。定義需要對(duì)加法器結(jié)果的和進(jìn)行加1的運(yùn)算為和加一運(yùn)算。為了消除對(duì)加法器結(jié)果的加一運(yùn)算,需要研究和加一運(yùn)算的性質(zhì)。
3.2 和加一運(yùn)算
考慮和加一運(yùn)算的重要性,定義和加一運(yùn)算的進(jìn)位信號(hào)為CA,則第i位的進(jìn)位信號(hào)為CAi。CAi信號(hào)與原本的c(i)信號(hào)是有聯(lián)系的:如果c(i)=1,顯然 CAi=1;如果 c(i)=0,而且 i-1…..0組不“殺死“進(jìn)位,即=1,則 CAi=1,所以 CAi=。由以上描述可得:

將式3代入得到:

其中,inc為和加一運(yùn)算控制信號(hào)。所以和加一運(yùn)算的求和公式為SAi=CAi8Pi,其中SAi為A與B和加一運(yùn)算結(jié)果的第i位。
輸出邏輯如圖3所示。
4 子字并行絕對(duì)值單元的設(shè)計(jì)
通過(guò)分析加法器的結(jié)構(gòu)可知,要想實(shí)現(xiàn)子字并行運(yùn)算,最重要的是要控制低位子字的進(jìn)位對(duì)高位子字產(chǎn)生影響。例如,在AltiVec指令集中,基于字節(jié)運(yùn)算的指令要消除在7+8*i(0≤i≤15)位上產(chǎn)生的進(jìn)位。所以,需要一個(gè)控制邏輯來(lái)控制低位進(jìn)位需不需要傳播到高位,對(duì)于32位字,對(duì)最短子字長(zhǎng)度為8的加法器單元,通過(guò)給出的控制信號(hào),可以同時(shí)計(jì)算4個(gè)字節(jié),或2個(gè)半字,或一個(gè)字的加法。如表1所示。
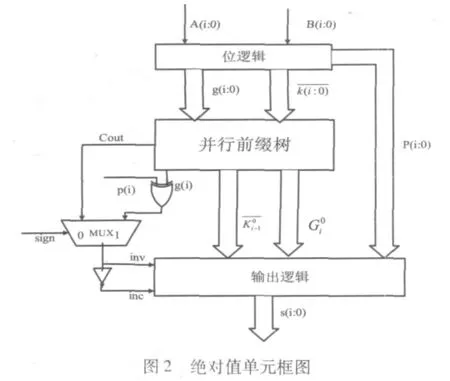
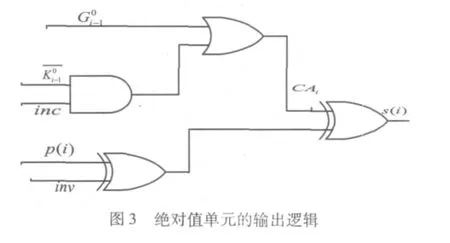

表1 控制信號(hào)
在一般的子字并行加法器設(shè)計(jì)中,控制邏輯只要控制了進(jìn)位的傳播就能實(shí)現(xiàn)子字并行加法。當(dāng)需要進(jìn)行子字加法時(shí),屏蔽相鄰位的進(jìn)位;反之,允許進(jìn)位。基于此原理,提出了進(jìn)位控制機(jī)制:進(jìn)位截?cái)鄼C(jī)制[1]。該方法的思想是,在并行前綴加法器的并行前綴樹結(jié)構(gòu)中,當(dāng)需要進(jìn)行子字并行運(yùn)算時(shí),控制低位的進(jìn)位對(duì)高位的影響,即在子字的邊界處設(shè)置控制信號(hào),消除進(jìn)位的傳播。
參照這種思想,對(duì)于子字并行絕對(duì)值的運(yùn)算也可以通過(guò)設(shè)置控制位截?cái)噙M(jìn)位的方式來(lái)實(shí)現(xiàn)。通過(guò)比較分析,子字并行絕對(duì)值單元在絕對(duì)值單元上做如下改進(jìn):
(1)采用與子字并行加法器相似的進(jìn)位截?cái)鄼C(jī)制,根據(jù)控制信號(hào)的有無(wú)決定是否將低位的進(jìn)位信號(hào)傳遞到高位。
(2)根據(jù)絕對(duì)值運(yùn)算的特點(diǎn),需要獲得最小子字(8位)進(jìn)位和符號(hào)位。以決定對(duì)結(jié)果進(jìn)行取反還是加一操作。
通過(guò)以上分析可知,子字并行絕對(duì)值單元的結(jié)構(gòu)框圖如圖4所示。
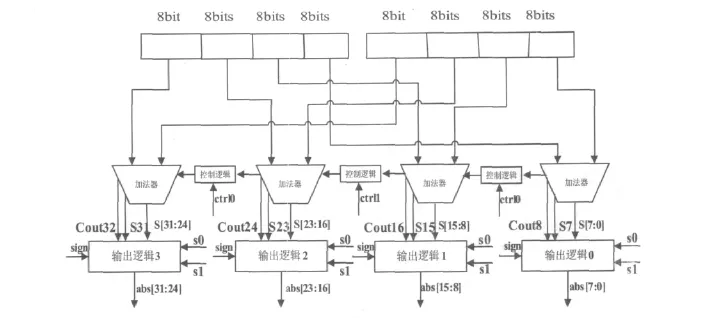
圖4 32位子字并行絕對(duì)值單元
輸出邏輯如圖3,由于要實(shí)現(xiàn)子字并行,所以相應(yīng)的inc和inv如下:
輸出邏輯0:inv0_7=(inv8&~S0&~S1)|(inv16&S0& ~S1)|(inv32&S0&S1);
輸出邏輯1:inv8_15=(inv16&~S0&~S1)|(inv16&S0& ~S1);
輸出邏輯2:inv16_23=(inv24&~S0&~S1)|(inv32&S0& ~S1)|(inv32&S0&S1);
輸出邏輯3:inv24_31=(inv32&~S0&~S1)|(inv32&S0&S1)
其中 invx=sign?sx-1:coutx(x 為8,16,32)
5 實(shí)現(xiàn)與性能分析
5.1 實(shí)現(xiàn)
采用verilog語(yǔ)言實(shí)現(xiàn)了以上討論的32位子字并行絕對(duì)值單元的可綜合設(shè)計(jì),同時(shí)實(shí)現(xiàn)了前面所討論的其它可實(shí)現(xiàn)絕對(duì)值單元的方法,并使之并行化。文獻(xiàn)[7]中沒(méi)有經(jīng)過(guò)優(yōu)化的絕對(duì)值單元為方案1,文獻(xiàn)[8]中采用條件加法器思想的絕對(duì)值單元為方案2,經(jīng)過(guò)優(yōu)化的絕對(duì)值單元為方案3。使用Modelsim對(duì)3種方案的設(shè)計(jì)進(jìn)行仿真,仿真數(shù)據(jù)的輸入采用隨機(jī)數(shù),運(yùn)算模塊的輸出結(jié)果同相對(duì)應(yīng)的行為級(jí)的輸出結(jié)果比較,結(jié)果全部正確。為了比較3種方法的面積與延時(shí),采用synopsys Design Complier[9]工具進(jìn)行邏輯綜合,為了體現(xiàn)公平性,所有絕對(duì)值單元中的加法器結(jié)構(gòu)都是用ladner-Fischer前綴加法器,不采用 synopsys DesignWare[10]中的基本加法單元。在TSMC 0.13um工藝下對(duì)這三種方案的子字并行絕對(duì)值進(jìn)行了實(shí)現(xiàn)并測(cè)試了它們的性能,時(shí)序/面積報(bào)告如表2所示:
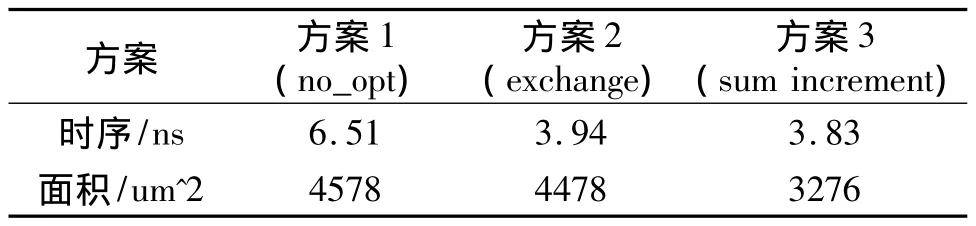
表2 子字并行絕對(duì)值單元時(shí)序/面積報(bào)告
三種方案的絕對(duì)值單元的時(shí)序/面積報(bào)告如表3所示。
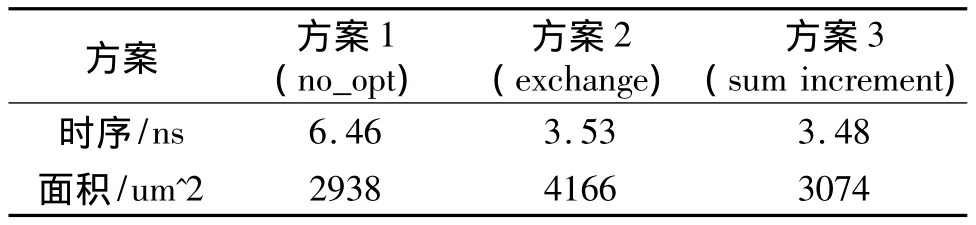
表3 絕對(duì)值單元時(shí)序/面積報(bào)告
5.2 性能分析
通過(guò)時(shí)序/面積報(bào)告可以看出,沒(méi)有實(shí)現(xiàn)子字并行的絕對(duì)值單元中,方案1的面積與方案3的面積相當(dāng),但方案3的時(shí)序明顯好于方案1。方案2的時(shí)序與方案3相當(dāng),但方案3的面積比方案2小很多。從前面分析可知,方案2采用了兩個(gè)加法器同時(shí)計(jì)算A-B和B-A,所以面積大了很多,而方案1是采用時(shí)間換取面積的方式,通過(guò)加法器計(jì)算結(jié)果來(lái)進(jìn)行下一步運(yùn)算,所以它的延時(shí)較大。方案3綜合了前兩種方案的優(yōu)點(diǎn),所以它的延時(shí)與面積都與前兩種方案的最好形式相當(dāng)。通過(guò)對(duì)和加一運(yùn)算的分析,使得在加法器的運(yùn)算過(guò)程中可以同時(shí)進(jìn)行A+B和A+B+1運(yùn)算,所以采用方案3方法實(shí)現(xiàn)的絕對(duì)值單元在減小面積的同時(shí),也減小了整個(gè)運(yùn)算單元的延遲。
子字并行絕對(duì)值單元是在絕對(duì)值單元的基礎(chǔ)上增加了一些控制低位進(jìn)位的邏輯,所以延時(shí)和面積較絕對(duì)值單元要大一些,但增加的不是很明顯。相比較其它方案,方案1中,子字并行絕對(duì)值單元的面積比絕對(duì)值單元大了很多。這是因?yàn)榉桨?中的絕對(duì)值單元是在加法器結(jié)果出來(lái)后,通過(guò)判斷加法器的進(jìn)位或符號(hào)位來(lái)決定對(duì)結(jié)果取反還是加一。因?yàn)槊恳粋€(gè)加法器模塊后面都有一個(gè)實(shí)現(xiàn)加一運(yùn)算的加法器,為了實(shí)現(xiàn)子字運(yùn)算,每個(gè)相應(yīng)的8位,16位和32位子字都需要這樣的加一運(yùn)算,所以導(dǎo)致方案1的面積大大增加。
6 結(jié)束語(yǔ)
子字并行運(yùn)算作為加速多媒體運(yùn)算的有效方式,在各種媒體處理(比如音頻和視頻)需要的大量運(yùn)算中得到了充分利用。該文分析了基于前綴加法器的子字并行絕對(duì)值單元的實(shí)現(xiàn)方法,并重點(diǎn)介紹了優(yōu)化絕對(duì)值單元中的和加一運(yùn)算,結(jié)合前綴加法器的特性,使得加法器可以同時(shí)進(jìn)行A+B和A+B+1運(yùn)算。分別實(shí)現(xiàn)了各種絕對(duì)值單元和子字并行單元并進(jìn)行了比較。結(jié)果顯示:優(yōu)化的子字并行絕對(duì)值單元在面積上克服了條件絕對(duì)值單元的不足,同時(shí)又保持了條件絕對(duì)值單元犧牲面積所帶來(lái)的時(shí)序優(yōu)勢(shì),在整體性能上優(yōu)于前文提出的絕對(duì)值單元。
[1] 馬勝,黃立波,王志英,等.子字并行加法器的研究與實(shí)現(xiàn)[J].計(jì)算機(jī)工程與應(yīng)用,2009,45(36):54-58.
[2] N Burgess.The flagged prefix adder and its application in integer arithmetic[J].VLSI Signal Process,2002,31(3):263-271.
[3] Neil H.E.Weste,David Harris.CMOS超大規(guī)模集成電路設(shè)計(jì)[M].汪東,等譯.北京:中國(guó)電力出版社,2006.
[4] Weinberger A,Smith J L A.A logic for high-speed addition[J].National Bureau of Standards Circular,1958,591:3-12.
[5] Beaumont-Smith A,Um C C.Parallel prefix adder design[C].Pro-ceedings of 15th IEEE Symposium on Computer Arithmetic,2001:218-225.
[6] Ladner R E,F(xiàn)ischer M J.Parallel prefix computation[J].ACM,1980,27(4):831-838.
[7] Carlson,D.A,Castelino,R.W,Mueller,R.O.Multimedia extensions for a 550-MHz RISC microprocessor[J].IEEE Journal of Solid-State Circuits,1997,32(11):1618-1624.
[8] S.C.Knowles.Arithmetic processor design for the T9000 Transputer[C].Proc.SPIE,1991:230-243.
[9] Synopsys Inc.Design compiler user guide[M].Mountain View:Synopsys,2007.
[10] Synopsys Inc.DesignWare building block IP user guide[M].Mountain View:Synopsys,2007.

