基于奇異值求通解方法進行基因調控網絡構建

沈威 ，鄭明，劉桂霞，邢翀，吳佳楠，周春光，周柚

(1. 吉林大學 計算機科學與技術學院，吉林 長春，130012；2. 北華大學 計算機科學技術學院，吉林 長春，132021)

隨著互補基因技術(cDNA)和微陣列技術的進步，人們已經能夠在整個基因組范圍內進行基因調控網絡的構建。這些通過實驗獲得的數據提供了在一些特定時間點各種不同的生化環境下基因表達的、很有價值的描述。并且這些數據讓研究者能從基因的時序表達值下推斷基因調控網絡。盡管如此，需要的基因調控網絡是存在于基因組中的成千上萬的基因所構成的網絡，極其復雜。所以，在系統生物學中一項極具挑戰的工作就是從各種數據尤其是時序數據中推斷出基因調控網絡。在可觀測系統和從算法中獲得的網絡之間是存在差異的，這種差異導致了算法精確度的差異，目前很難提供一個高度精確的算法來實現對任意實驗數據的網絡推斷。盡管如此，研究更精確的網絡推斷模型仍然是生物信息學的研究熱點。許多方法被提出并應用在基因調控網絡推斷上，這些方法包括布爾網絡[1]、貝葉斯網絡[2-3]和微分方程模型[4]等。布爾網絡提供了一種網絡結構關系的概念層方法，網絡一般規模龐大，常常包含成百上千的基因，但是，網絡中節點的狀態只有開和關2種狀態。貝葉斯網絡是一種能夠描述網絡關系的概率模型，網絡模型中每條邊都存在1個概率，貝葉斯網絡的圖形構成的是1個有向無環圖，節點一般包括幾十個節點，規模適中。微分方程模型則是一種高度精確的網絡構建模型，以變化率的形式表示出各個基因的影響關系，是一個動態方程組。 這種方式構成的網絡往往只包含幾個基因，一般在20個以內，所構成的網絡在數學上最精確，即規模小而精。但是無論采用哪種方法，仍然存在精度不高的問題，因此，需要一個更好的方法來進一步改進微分方程模型。改進策略之一是改變方程的形式，如把方程中某個參數進行分解或改變，更可以把微分問題化為積分問題[5]等，但這種策略在本質上并沒有改變精度。另一種改進策略是引入奇異值分解(SVD)[6]的方法。在運算過程中把方程組中表達數據所構成的矩陣或其轉置矩陣進行分解，之后進行矩陣運算并得到符合奇異值分解規則的解即權值矩陣作為最終網絡結果。在多個基因的實驗數據條件下，方程組的解往往并不唯一，而奇異值分解求出的是惟一解，這個解可能在無數解集中并不是最優解。針對這個問題，本文作者在通過奇異值分解求得的特解基礎上求出符合奇異值分解規則的通解即解的集合，并把這個通解作為一個取值范圍，結合改進形式的微分方程模型策略用優化算法求解和優化網絡的權值矩陣并得出網絡的最終結果。

1 算法的數學框架

用于推斷網絡的方法可以分為2步。首先，要使用奇異值分解方法來構建一個解的集合。這個集合是由符合方程組規律的解集所組成的，如果規模很大，一般提供通解。然后，在這個集合或標準下進行模型的優化，使用線性回歸分析進行微分方程的求解，并最終得到所求網絡。

為了簡化，僅對穩態系統或者接近穩態的系統進行分析。構建網絡的數學模型采用的是微分方程模型。這個模型可以簡化為每個方程均為式(1)所示形式的方程所組成的方程組：

其中，xi(t)為基因i在時刻t的濃度；N為網絡所包含基因的總數；wij為基因j對基因i進行影響的權值參數，這個值是正數時表示正調控，負數時表示負調控，0表示在一定閾值范圍內可以視為不發生相互作用；bi表示在沒有調控輸入的情況下基因 i的變化，也包括了外界對基因i的刺激所產生的表達濃度的變化。

在實驗中，可以提供一些恒定的外界刺激，即bi是恒定的。為了方便，更多的時候設定bi為0，即不施加任何外界刺激。然后，對N個基因在T個時間段進行測量，即得到所需數據，數據組織形式如下：

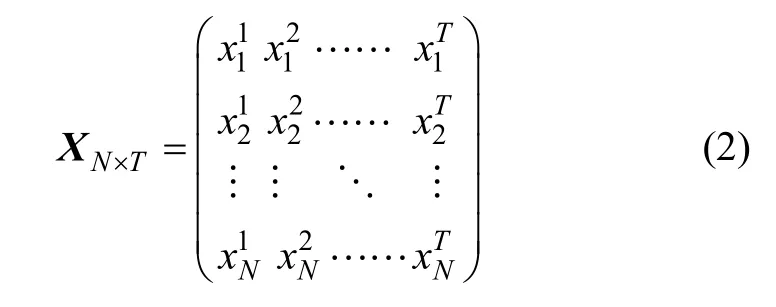
其中：x為基因表達濃度；下標表示基因標識，上標表示測試時間序列；共有N個基因、T個時間測試點。根據式(2)，式(1)可以寫成式(3)所示形式：

為了求出權值矩陣W，往往把方程組進行變形和改進，這可以在一定程度上提高精度，但要從根本上提高精度需要進行奇異值分解。可以將X矩陣進行奇異值分解：

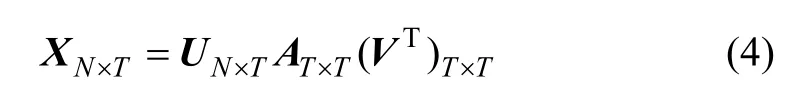
其中：矩陣A是一個不必滿足滿秩條件的對角矩陣。為了計算方便，可以在計算過程中進行調整，使得矩陣A中對角線上的值是按照大小進行排序的。即非零值第1個值最大，其他值遞減。后面的幾個對角線上的值為0，非對角線上的值全為0。對角線上零值的個數可以為 0，即此矩陣可以為滿秩矩陣。在式(4)中，奇異值分解得到的結果U與V都是正交矩陣，且都滿足：

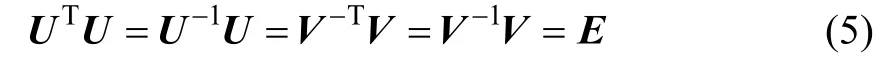
式中：E為單位矩陣。

對式(3)兩邊同時減BN×T，然后，方程兩邊同時右乘XN×T的逆矩陣，并把式(4)代入式(3)，得到：

在式(6)中，并不是每個矩陣都存在逆矩陣，特別是矩陣 U，這里的逆矩陣指的就是廣義逆矩陣[7]。在廣義逆矩陣定義下，任意一個矩陣都存在其逆矩陣。但其廣義逆矩陣往往不是方陣，更不是奇異陣。

由式(6)得到基因調控網絡構建所需的權值矩陣W。研究者們一般就把此特解作為最終的網絡結果，但該結果并不精確，因為符合式(6)條件的值很多，數量級很大，甚至無窮多解，即N＞＞T，這樣所求的值其實并不一定是最優解。在計算過程中，最好能夠盡可能多的得到解集或者取值范圍，并使用優化算法進行計算。本文算法在特解的基礎上，構造下式來求通解：

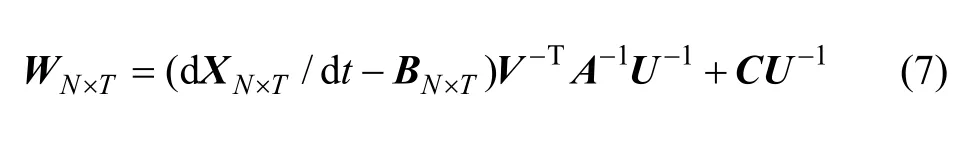
式中：C為任意常數。

構造了這個通解后，就可以得到所求解的取值范圍，從而可以修改微分方程模型，并計算優化，在此范圍內求得所求網絡。

從式(1)出發對權值矩陣 W 進行變形。首先需要定義此算法的能量函數，即誤差最小化函數。此誤差為所求值和觀測值之間的差：

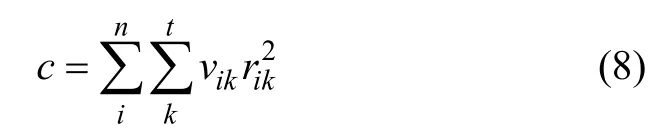
其中：rik為式(1)的殘基；vik為rik的1個權值，則

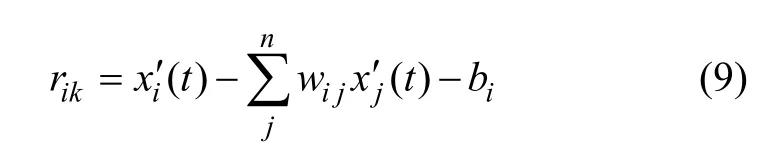
從式(9)可以看出：rik符合殘基概念。本文所要做的就是在式(7)所示的網絡權值取值范圍內使殘基最小化。得到所要進行的目標之后，需要把方程進一步改進，以便提高效率，較少誤差。在式(8)和(9)中，所需計算的只有wij，而網絡中共有N個基因且權值矩陣W為一方陣，則所需計算的參數為N個。一旦基因數過于龐大，則所需計算的參數個數將隨指數級增長，不適合求解，因此，需要把權值矩陣W進一步優化并分解，這樣權值w將變為：

經過式(10)的轉化之后，權值矩陣W中的值只與t和x這2個變量相關，從而使得計算非常簡便。

優化算法方面，本文采用粒子群算法[8]和遺傳算法[9]相結合的方式，通過最小化式(8)，求得最小值，然后驗證是否符合式(7)的方式，求得最終的網絡。

2 算法的實現

本文算法的實現部分用Java語言編寫，所用環境為MyEclipse 8.0版本。算法的流程步驟如下。

(1) 讀取基因表達數據，其格式符合國際表達數據標準(MIAME[10])。

(2) 對已經讀取的基因表達數據所構成的矩陣運用式(4)進行奇異值分解并得到式(4)中的U與V。

(3) 運用式(6)求得所需計算的權值矩陣W的特解W特，并根據式(7)求得W的通解W通。

(4) 隨機生成大量權值構成粒子群算法和遺傳算法的初始群體。并根據步驟(3)得到的取值范圍淘汰不符合要求的隨機權值。淘汰的權值重新生成，直到所有的隨機權值符合W通的條件為止。

(5) 運用式(10)分解權值，將權值降維為只有2個變量的方程組。并運用遺傳算法和粒子群算法(PSO)最小化式(8)，得到最小值。

(6) 若步驟(5)計算得到的值符合 W通的條件則算法終止，否則進入步驟(5)。

算法流程圖如圖1所示。

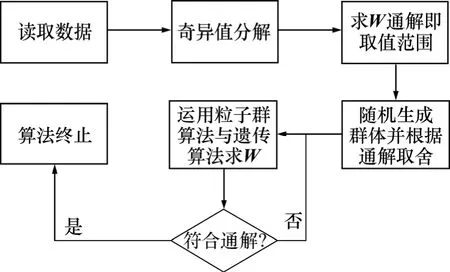
圖1 本文算法流程圖Fig.1 Flow chart of proposed algorithm

3 實驗結果與分析

3.1 測試方法

為了測試本文算法的效果，進行比較實驗。比較對象為單純使用式(1)的基本微分方程模型(方法 1)和代入式(10)的改進型微分方程模型(方法2)及本文模型(方法3)。這3種模型的比較實驗將分為模擬數據實驗和真實數據實驗2部分。

采用 Bansal等[11]所提出來的正預測值(PPV)和敏感度(SE)評價算法優劣。

3.2 模擬數據實驗

數據來源采用生成無標度網絡[12]后微分方程逆向反推基因表達數據的方法進行計算獲得。與隨機生成的網絡相比，無標度網絡更符合基因調控網絡的生物學現象。在生成的無標度網絡中，每個節點的連接數都接近于冪率分布 p(k)～k。本文用增加重導向自增算法[13]進行構建。參數r設定為3，節點數N為20。根據這種算法和參數構建的網絡如圖2所示。在圖2中，原點為節點0，逆時針依次為節點1，2，…，20。方塊的為有向線段末端，指向被調控節點。網絡生成以后，用式(1)來進行數據推斷，所有的bi均設置為0。數據的時間點設定為 50。隨機噪聲參數設定為-0.5～0.5之間。

由圖2所示的圖模擬出基因表達數據后，經過運算得到結果如圖3所示。在圖3中，所表示的含義與圖2的一樣，不同的是圓圈代表的是自我調控關系。

為了避免結果巧合，運行程序100次，并把N的取值定為 20。計算后取平均值并評估算法的優劣。3種方法的比較結果如表1所示。

從表1可知：本文算法(即方法3)的正預測值和敏感度明顯高于其他2種算法的結果，其運行時間也比其他2種方法的運行時間短。

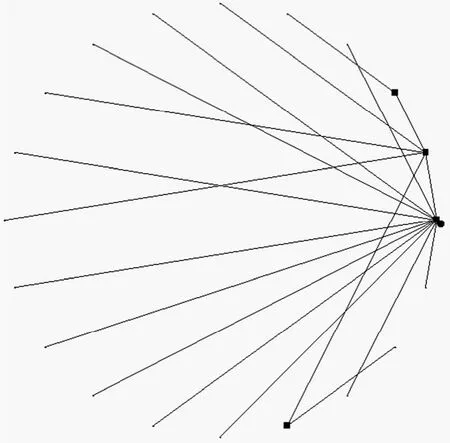
圖2 參數r=3，N=20的無標度網絡圖Fig.2 Scale-free network with parameter r=3, N=20

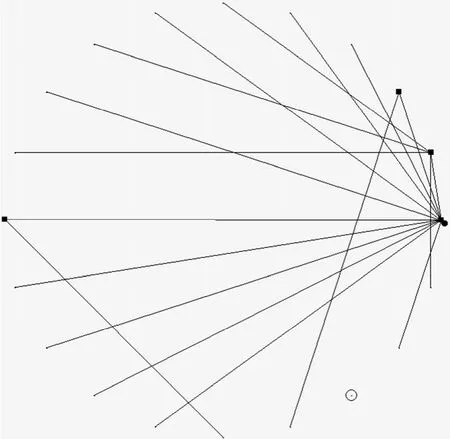
圖3 根據圖2所生成的數據所計算的基因調控網絡圖Fig.3 Gene regulatory network calculated with proposed algorithm from data simulated by Fig. 2

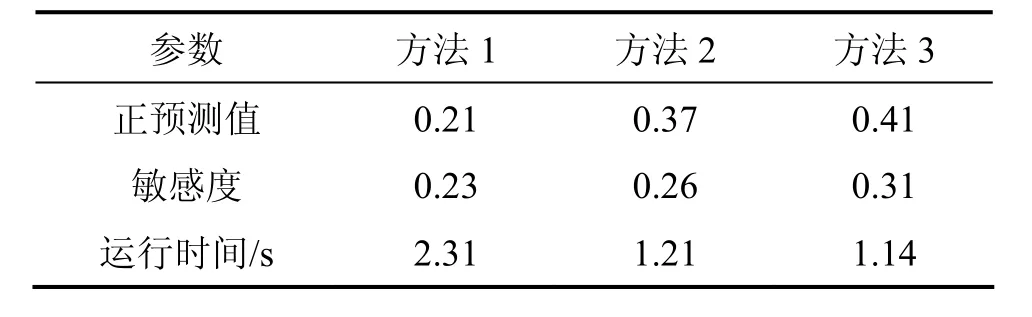
表1 3種算法模擬數據效果比較Table 1 Compared results of three kinds of algorithm in simulation data

方法2比方法1在運行時間上更有優勢的原因在于方法2把方法1中的N2個參數化簡為只有2個參數，使得運算時間大大縮短。本文方法為方法2提供了一個很好的候選解的集合，減少了方法2尋優的空間和運行時間，但是，由于奇異值分解運算本身消耗了一定的時間，因此，與方法2的運行時間相比，本文方法的運行效率略有提高。

3.3 真實數據實驗

真實數據的計算采用的是 GEO[14]基因表達數據庫上下載的基因表達數據，這里采用的是經典的酵母基因表達數據，即采用GDS38數據的子集，其表達的結果圖可以從日本KEGG[15]數據庫中的pathway里得到。這個數據包括3個子集，這3個子集包括3種實驗條件：Alpha，elu和cdc15，它們分別包括18，14和24個時間點。抽取出來的1個網絡子集如圖4所示。經過本文算法計算，對應圖4所生成的基因調控網絡如圖5所示。在圖5中，所有的含義與圖2中的一樣，原點作為第1個初始點，圓圈表示自調控，方塊表示被調控段。

圖4 KEGG數據庫的pathway中酵母基因調控網絡的1個子集圖Fig.4 A part of yeast cell cycle pathway available from KEGG

圖5 用本文算法算得的基因調控網絡圖(對應圖4)Fig.5 Gene regulated network calculated by proposed algorithm (according to Fig. 4)

根據式(1)和(10)的微分方程模型，運行100次后取平均值，最終結果如表2所示。

從表 2可以看出：本文算法(即方法 3)比其他 2種算法更優越。從運行時間上來看，本文算法比其他2種算法相比更小。與模擬實驗結果相比，優勢不是很明顯。

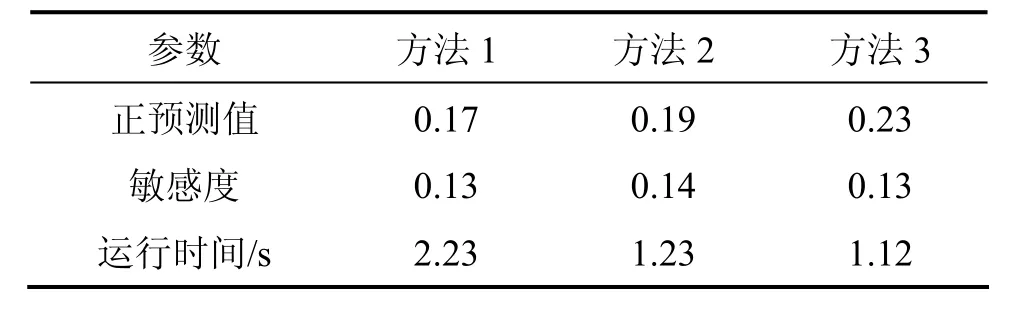
表2 3種算法運算真實數據結果比較Table 2 Compared results of three kinds of algorithm in real data

4 結論

(1) 提出了一種具有通解的構建基因調控網絡算法。這種新的融合算法不僅在運算過程中提供了一個候選解的集合，使得運算過程中免去了非解的不必要計算，縮短了運算時間，同時，使得運算結果更精確。通過與其他2種傳統微分方程模型算法的對比實驗，證實了本文算法的效率較高，符合預期結果。

(2) 本文算法的目標是從有限的數據中得到最接近于真實的基因調控網絡的結果，提高實驗水平。但是，本文的基因調控網絡算法整體的精度，還需進一步提高，這有待進一步研究。

[1] D’haeseleer P, Liang S, Somogyi R. Genetic network inference:from co-expression clustering to reverse engineering[J].Bioinformatics 2000, 16: 707-726.

[2] Dojer N, Gambin A, Mizera A, et al. Applying dynamic Bayesian networks to perturbed gene expression data[J]. BMC Bioinformatics, 2006, 7: 249.

[3] Beal M J, Falciani F, Ghahramani Z, et al. A Bayesian approach to reconstructing genetic regulatory networks with hidden factors[J]. Bioinformatics, 2005, 21: 349-356.

[4] Bansal M, Gatta G D, di Bernardo D. Inference of gene regulatory networks and compound mode of action from time course gene expression profiles[J]. Bioinformatics, 2006, 22:815-822.

[5] Eugene N, Emmanuel B. Regulatory network reconstruction using an integral additive model with flexible kernel functions[J].BMC Systems Biology, 2008, 2: 8.

[6] Nelson P A, Kahana Y. Spherical harmonics, singular-value decomposition and the head-related transfer function[J]. Journal of Sound and Vibration, 2001, 239(4): 607-638.

[7] Liang M L, Dai L F. The left and right inverse eigenvalue problems of generalized reflexive and anti-reflexive matrices[J].Journal of Computational and Applied Mathematics, 2010, 234:743-749.

[8] Brits R, Engelbrecht A P, van den Bergh F. Locating multiple optima using particle swarm optimization[J]. Appl Math Comput,2007, 189(2): 1859-1883.

[9] Chen D Y, Chuang T R, Tsai S C. Jgap: A java-based graph algorithms platform[J]. Software Pract Exper, 2001, 31(7):615-635.

[10] Tim F R, Philippe R S, Paul T S, et al. A simple spreadsheet-based, MIAME-supportive format for microarray data: MAGE-TAB[J]. BMC Bioinformatics, 2006, 7: 489.

[11] Bansal M, Belcastro V, Ambesi-Impiombato A, et al. How to infer gene networks from expression profiles[J]. Mol Sys Biol,2007, 3: 78.

[12] Barabási A L, Albert R. Emergence of scaling in random networks[J]. Science, 1999, 286: 509-512.

[13] Silva A C, da Silva J K L, Mendes J F F. Scale-free network with Boolean dynamics as a function of connectivity[J]. Phys Rev E,2004, 70(6): 66140-66147.

[14] Wilhite S E, Barrett T. Strategies to explore functional genomics data sets in IVCBI’s GEO database[J]. Methods Mol Biol, 2012,802: 41-53.

[15] KEGG Cell cycle-yeast-Saccharomyces cerevisiae[EB/OL].[2010-04-13].http://www.genome.jp/kegg/pathway/sce/sce0411 1.html.