格構錨固邊坡地震響應的振動臺試驗研究

楊果林，文暢平,

(1. 中南大學 土木工程學院，湖南長沙，410075；2. 中南林業科技大學 土木工程與力學學院，湖南長沙，410004)

建設中的大(理)—瑞(麗)鐵路沿線有大量基覆邊坡(厚覆蓋層和基巖)，需要采用相應的工程措施對其進行支護，格構錨桿框架支護邊坡是其中的措施之一。該鐵路位于云南滇西地區，屬于高烈度地震多發區，因而需要對沿線的格構錨桿框架支護邊坡在地震作用下的動力特性進行研究，為工程設計提供科學依據。巖土邊坡動力變形和破壞問題一直是巖土工程和地震工程主要的研究課題，研究方法主要有模型試驗和數值分析。邊坡動力模型試驗方法主要有3種：爆炸模型試驗、離心模型試驗和振動臺模型試驗。由于振動臺模型試驗[1-2]是在地震模擬振動臺上輸入設計地震波，直接由臺面推動測取模型動力特性，因而較好地模擬了地震動力問題，并且能準確再現地震波波形、自動和精確地采集試驗數據，無限次地進行地震模擬。盡管振動臺模型試驗難以解決重力相似問題，但仍然是研究邊坡與支擋結構地震變形和破壞問題以及檢驗數值分析結果的重要手段之一[3-9]。由于通過大型振動臺模型試驗對邊坡和支擋結構的地震動力問題進行的研究較少，本文作者以大瑞鐵路沿線格構錨桿框架支護邊坡為研究對象，以汶川波作為設計輸入地震波，在邊坡模型中布置加速度、動位移和動土壓力傳感器，進行大型振動臺模型試驗。試驗旨在研究地震作用下格構錨桿框架支護邊坡的加速度動力響應、動位移和動土壓力響應特性。

1 振動臺模型試驗

試驗在重慶交通科研設計院橋梁工程結構動力學國家重點實驗室進行，該試驗室的地震模擬振動臺為大型高性能3軸向6自由度寬頻域地震模擬臺陣系統，單個臺面尺寸為3 m×6 m(寬×長)，承載的最大試件質量為350 kN，工作頻率為0.1～50 Hz，水平和豎直向最大位移分別為150 mm和100 mm，水平和豎直向最大速度分別為800 mm/s和600 mm/s，水平和豎直向最大加速度為1g(1g=9.8 m/s2)。

試驗擬采集的數據包括：加速度、位移、土壓力，利用 Dewetron2010 動態測試數據采集系統自動采集和存儲3種傳感器的響應數據。

1.1 相似關系設計

本模型試驗的控制量為幾何尺寸、密度和加速度，其相似常數分別取Cl=8，Cρ=1，Ca=1，模型與原型尺寸的相似比為 1:8，按照相似理論和量綱分析方法[10-12]，確定其余物理量的相似常數如表1所示。

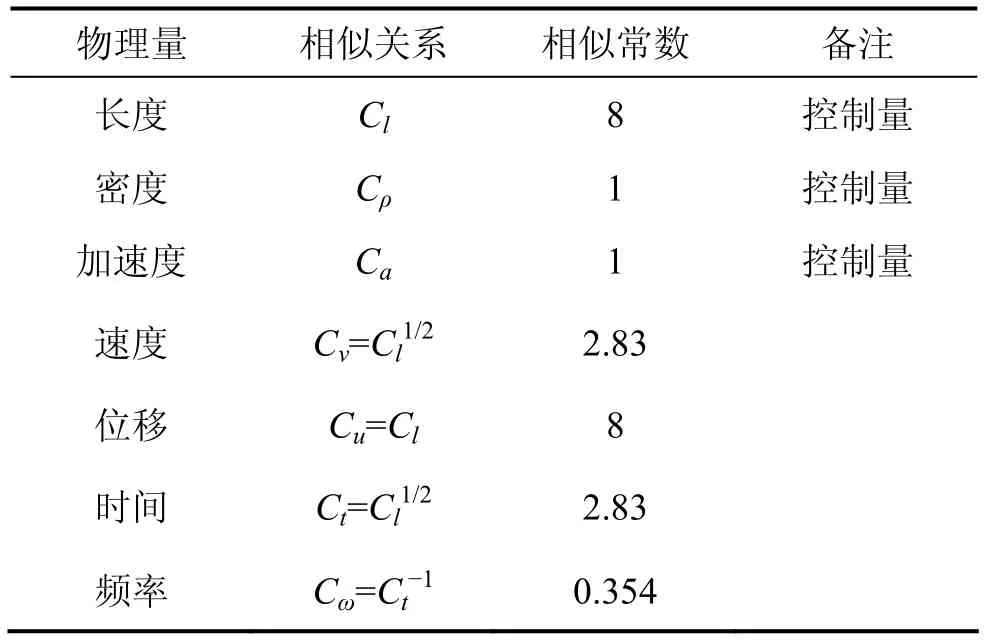
表1 振動臺模型試驗相似常數Table 1 Similarity coefficients of shaking table test

1.2 模型設計與傳感器布設

本模型試驗模擬的原型邊坡為大瑞鐵路 DK10＋400～DK11＋535段基覆邊坡。該段邊坡地層為碎石土，其碎石為花崗片麻巖，最大粒徑為16～20 cm，含量約65%，土質為黏性土，屬Ⅲ級硬土。碎石土的天然重度 γ=21 kN/m3，黏聚力c=0 Pa，內摩擦角 φ=35°。本試驗模擬邊坡高度為12 m，坡度為1:1.25。根據表1的模型相似關系，模型邊坡尺寸設計為 150 cm(高)×150 cm(寬)，邊坡坡率 1:1.25。

試驗采用鋼板、型鋼和有機玻璃制作的一端開口的剛性模型箱，內空尺寸為 340 cm×150 cm×210 cm(長×寬×高)。邊坡模型及其詳細尺寸、模型箱和邊坡模型全貌分別如圖1～3所示。

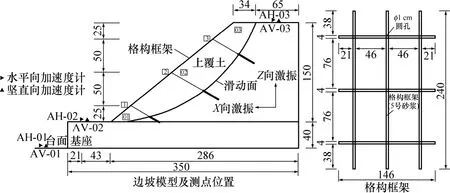
圖1 邊坡模型及測點位置圖(單位：cm)Fig.1 Slope model and the locations of transducers

圖2 剛性模型箱Fig.2 Rigid model box

圖3 模型邊坡全貌Fig.3 Overall perspective of test model

試驗設置12個加速度傳感器，6個動位移傳感器和4個動土壓力傳感器，分別測定模型邊坡加速度動力響應、護坡動位移和邊坡土體動土壓力響應特性。所有傳感器沿模型邊坡中軸線縱剖面布設，01點距基座6 cm，03點距坡頂10 cm，其余測點位置見圖1。在格構框架上的1，2和3點等處，設置的水平方向加速度傳感器編號為AH1，AH2，AH3；豎直方向的加速度傳感器編號為 AV1，AV2，AV3；設置的水平方向動位移傳感器編號為DH-1，DH-2，DH-3；豎直方向動位移傳感器編號為 DV-1，DV-2，DV-3。在坡內的01，02和03點等處，設置的水平方向加速度傳感器編號為 AH01，AH02，AH03；豎直方向的加速度傳感器編號為AV01，AV02，AV03；設置的水平方向動土壓力傳感器編號分別為FH1，FH2，FH3。此外，在 02點處增設豎直方向動土壓力傳感器，編號為FV2。

在臺面、基座底面和頂面分別布設了3個水平方向和3個豎直方向加速度傳感器，編號分別為AH-01，AH-2，AH-03以及AV-01，AV-02，AV-03。傳感器型號詳細說明見表2。

表2 模型試驗傳感器型號說明Table 2 Specification of each transducer

1.3 試驗材料的選取

在模型箱底部澆注高度40 cm的C25混凝土，其上再澆筑表面為圓弧面的C25混凝土，以模擬基質巖層，并將錨桿預埋其中。試驗用土為碎石土，土石質量比為4:6，填筑壓實度為90%，碎石最大粒徑≤2cm，土的最大干密度 ρdmax=2.18 g/cm3，土的最佳含水量wopt=5.34%，c=6.2 kPa，φ=34°。格構框架梁截面為 4 cm的正方形，材料采用加氣微粒混凝土，設計抗壓強度為5 MPa，混凝土內鋼筋和錨桿以直徑4 mm的鐵絲模擬。

1.4 地震波輸入及加載制度

試驗采用的地震波有3種：汶川波、大瑞人工合成波和Kobe波。本文主要探討汶川波(2008，代號為WC)作用下，邊坡加速度動力響應、動位移和動土壓力響應特性。汶川波分別采用水平單向(X向)、豎直單向(Z向)和水平豎直雙向(XZ向)(由X和Z向合成)3種方式加載，代號分別為：WC_X，WC_Z和WC_XZ。激振方向X向和Z向見圖1所示，地震波的時間壓縮比為 2.83。汶川波具有較豐富的高頻成分，在小于0.15 s的短周期范圍內，其豎向反應譜比水平規范譜大，而長周期范圍內則小很多，其主震持時約為20 s，主頻約為5 Hz。汶川波加速度時程曲線見圖4。

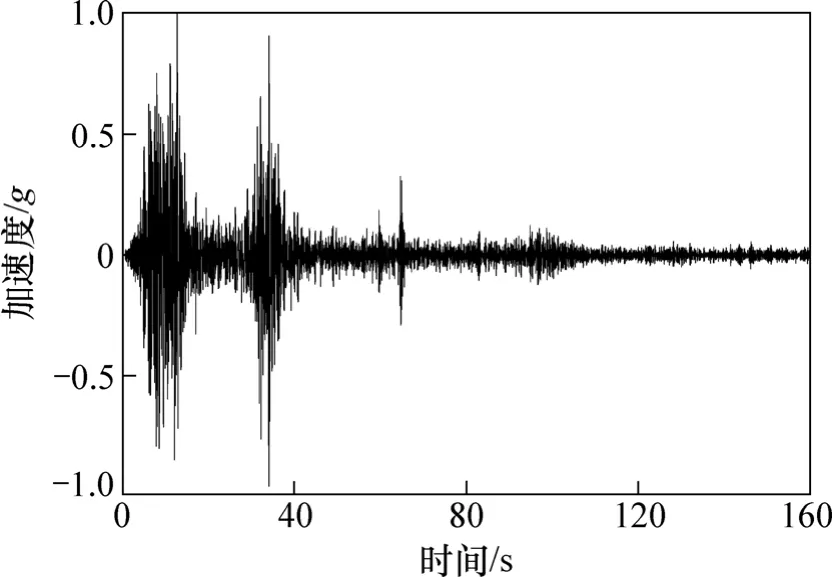
圖4 汶川波加速度時程曲線Fig.4 Time-history of Wenchuan seismic wave

試驗研究的地震烈度為VII～X，根據文獻[13-14]，將相應的加速度峰值調整為：0.1g，0.2g，0.4g和0.6g。試驗在此基礎上增加了0.8g和1.0g 2種工況，并采用逐級施加地震加速度的方式進行。當X向加載時，按上述加速度峰值逐級加載；當Z向加載時，按X向峰值的2/3折減后逐級進行加載。具體加載制度見表3。

2 邊坡加速度動力響應規律

由于每次地震波加載后，臺面實測水平和豎直向加速度峰值與激振加速度峰值基本吻合，表明試驗是可靠的。此外，由于混凝土基座對臺面水平和豎直加速度存在一定的放大效應，且豎直方向表現明顯，因此，在進行模型加速度動力響應分析時，以臺面加速度傳感器響應峰值作為控制點。

以 PGA[15-17]的響應峰值放大系數(Amplification of PGA，記為PGAA)進行邊坡模型加速度動力響應分析。規定：X向單向激振時，PGAA為測點加速度響應峰值與臺面X向響應峰值實測值的比值；Z向單向激振時，PGAA為測點加速度響應峰值與臺面Z向響應峰值實測值的比值；XZ雙向激振時，X向PGAA為測點與臺面X向響應峰值實測值的比值，Z向PGAA為測點與臺面Z向響應峰值實測值的比值。

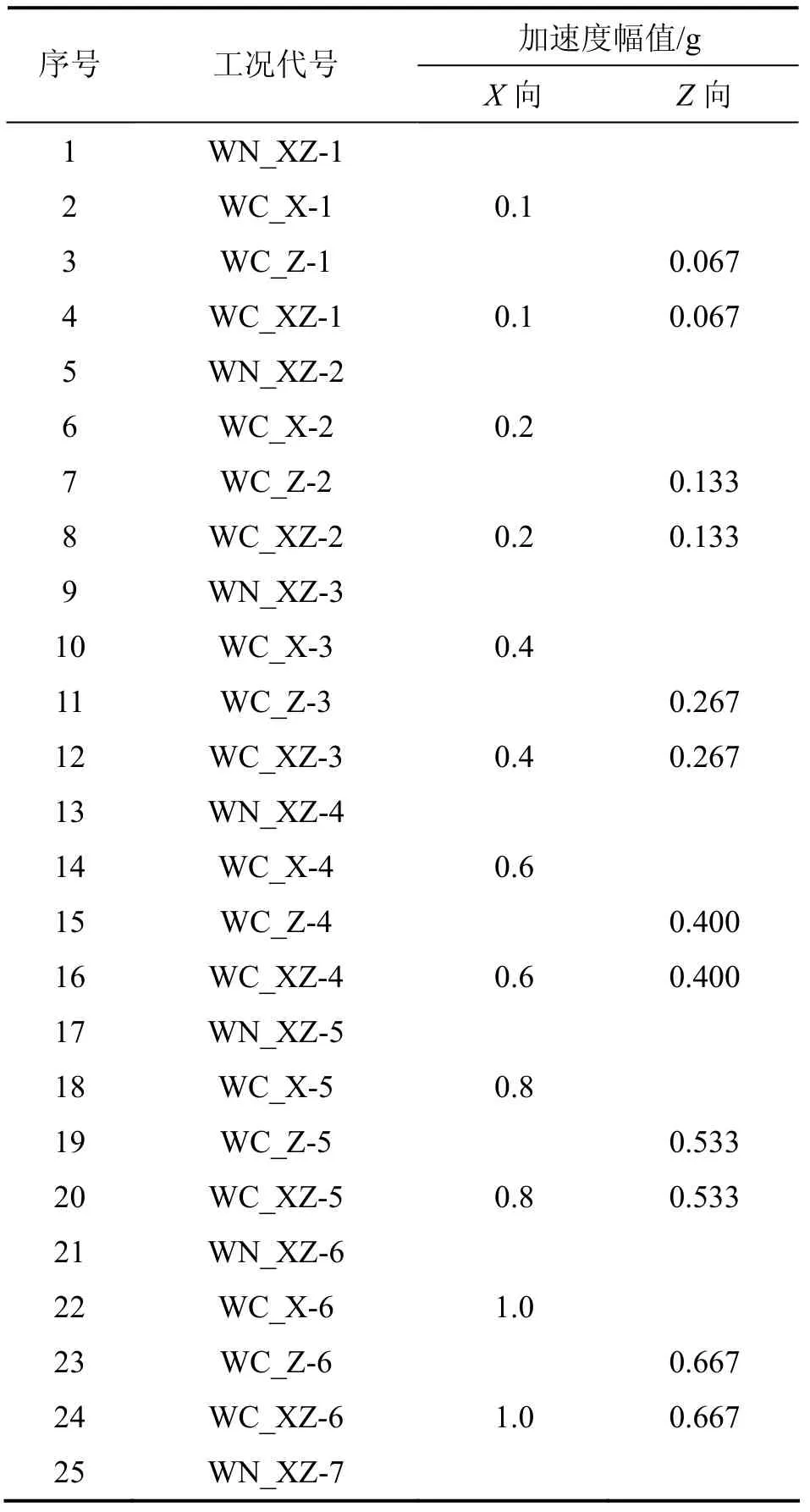
表3 振動臺模型試驗加載制度Table 3 Loading rule of shaking table test

2.1 邊坡水平方向加速度響應規律

汶川波3種加載方式下，護坡和坡體內各測點X向PGAA隨激振加速度的響應規律如圖5和圖6所示，X向PGAA隨坡高的響應規律如圖7和圖8所示。由圖7和圖8可見：在X向激振下，6個測點的X向PGAA隨激振加速度增大呈現出非線性特征，坡體內各測點的X向PGAA大于護坡，即坡內動力響應強度大于坡面。護坡中下方(AH1和AH2)X向PGAA在激振加速度峰值AXmax≤0.4g時小幅增大，AXmax＞0.4g時小幅減小；上方(AH3)的X向PGAA在AXmax≤0.6g時隨激振加速度增大而增大，AXmax＞0.6g時則小幅減小。對于坡體來說，邊坡中下部(AH01和AH02)X向PGAA變化平緩，而邊坡上部(AH03)則隨激振加速度增幅較大。

高程對邊坡地震動力響應顯著，X向PGAA隨坡高表現出非線性增大的特征，但是，AXmax≤0.4g時增大的幅度小于AXmax≥0.6g時的情形。

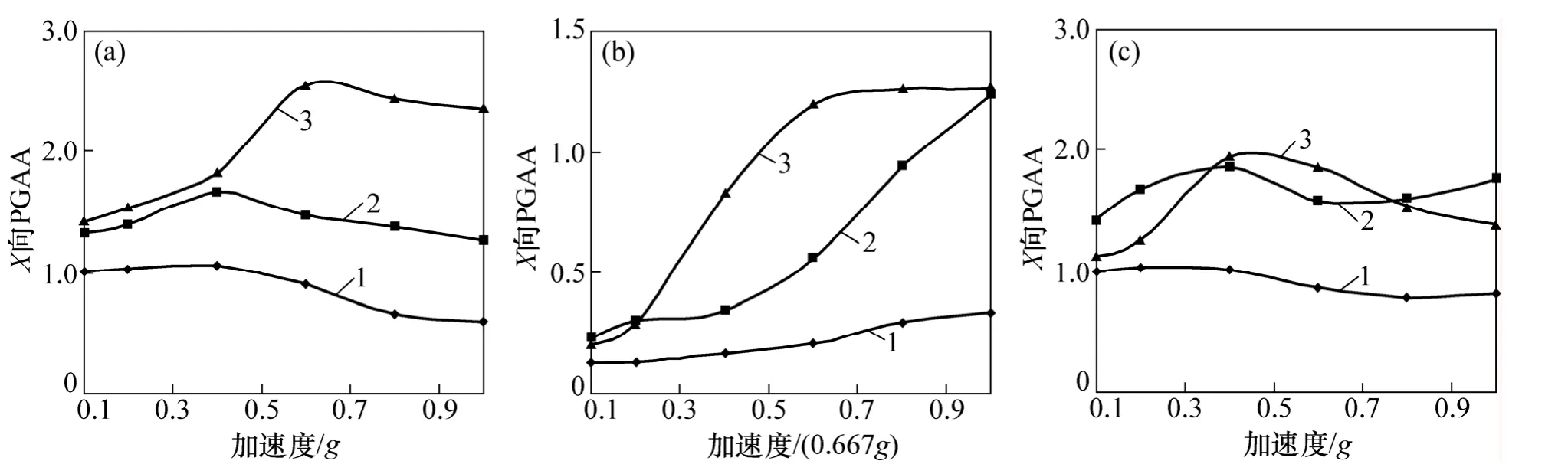
圖5 護坡X向PGAA隨激振加速度響應規律Fig.5 Response mechanism of X-PGAA of lattice frame with peak exciting acceleration

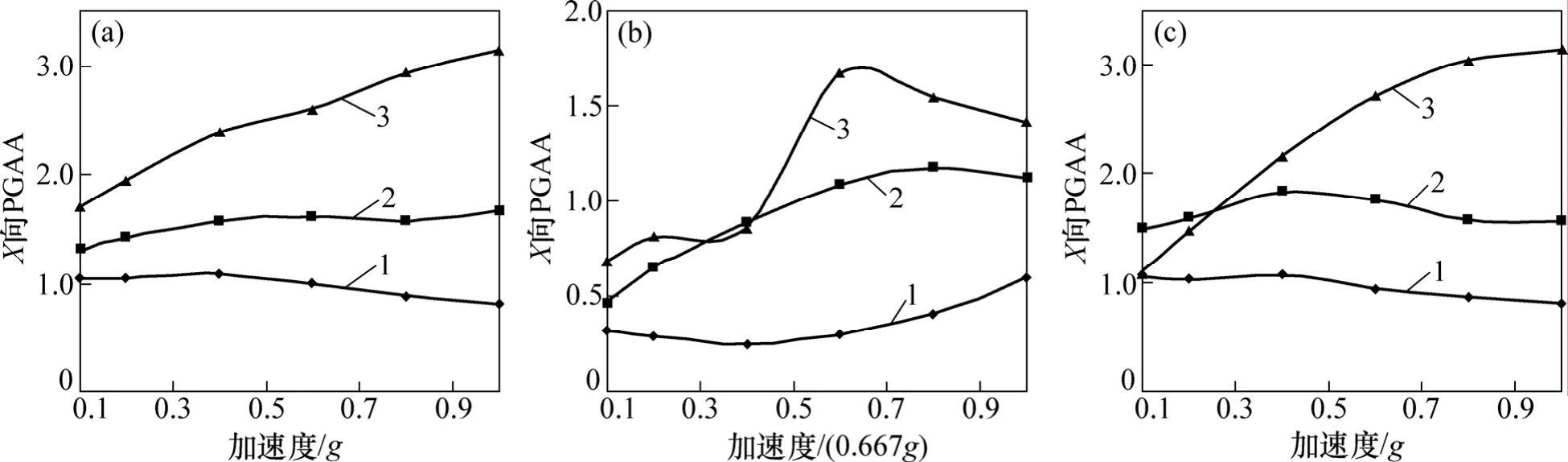
圖6 坡體X向PGAA隨激振加速度響應規律Fig.6 Response mechanism of X-PGAA in slope with peak exciting acceleration

圖7 護坡X向PGAA隨坡高響應規律Fig.7 Response mechanism of X-PGAA of lattice frame with slope height

在Z向激振下，激振加速度峰值AZmax≥0.267g時在邊坡中部和上部產生較大的水平方向加速度放大效應，且坡內動力響應程度同樣比坡面的大。

高程對邊坡地震動力響應也較為明顯，X向PGAA隨坡高同樣表現出非線性特征。除 AZmax≤0.133g時護坡上方X向PGAA有減小的趨勢，其他加載方式下則隨坡高非線性增大。

在XZ向激振下，只有當AXmax≥0.6g時AH03的PGAA繼續增大外，其余加載條件下其他測點的PGAA變化不大。邊坡中下方坡內外動力響應程度基本一致，而上方坡內動力響應程度比坡面的強。從高程對邊坡水平地震動力響應特征來看，邊坡下部和中部響應特征相同，即X向PGAA隨坡高而增大。邊坡上部響應特征多變：護坡X向PGAA除AXmax=0.6g增大外，其余情況下都隨坡高而減小；坡體X向PGAA除AXmax≤0.2g減小外，其余情況則是隨坡高而增大。這與文獻[17-19]中的結論不完全一致。

此外，汶川波XZ向激振下，各測點PGAA并不大于X向單向激振時的情形。

通過上述分析得出：模型邊坡X向加速度的放大主要是由于水平方向地震波引起的，并且這種放大效應主要體現在邊坡中上方，這與文獻[19-20]中的研究結論一致。豎直方向地震波在AZmax≥0.267g時，也會對邊坡水平方向加速度產生較大的放大效應。

2.2 邊坡豎直方向加速度響應規律

汶川波3種加載方式下，護坡和坡體內各測點Z向PGAA隨激振加速度的響應規律如圖9和圖10所示，Z向 PGAA隨坡高的響應規律如圖 11和圖 12所示。

從圖9～12可見：在X向激振下，邊坡上方Z向PGAA較為接近X向PGAA，其他測點也產生較大的豎直方向加速度響應，表明X向激振時，水平和豎直方向都產生加速度動力響應[21]。此時坡內外加速度動力響應程度基本一致。Z向PGAA隨坡高響應表現出非線性特征。邊坡中部Z向PGAA最小，上部最大，呈現出兩頭大中間小的特征。

圖8 坡體X向PGAA隨坡高響應規律Fig.8 Response mechanism of X-PGAA in slope with slope height

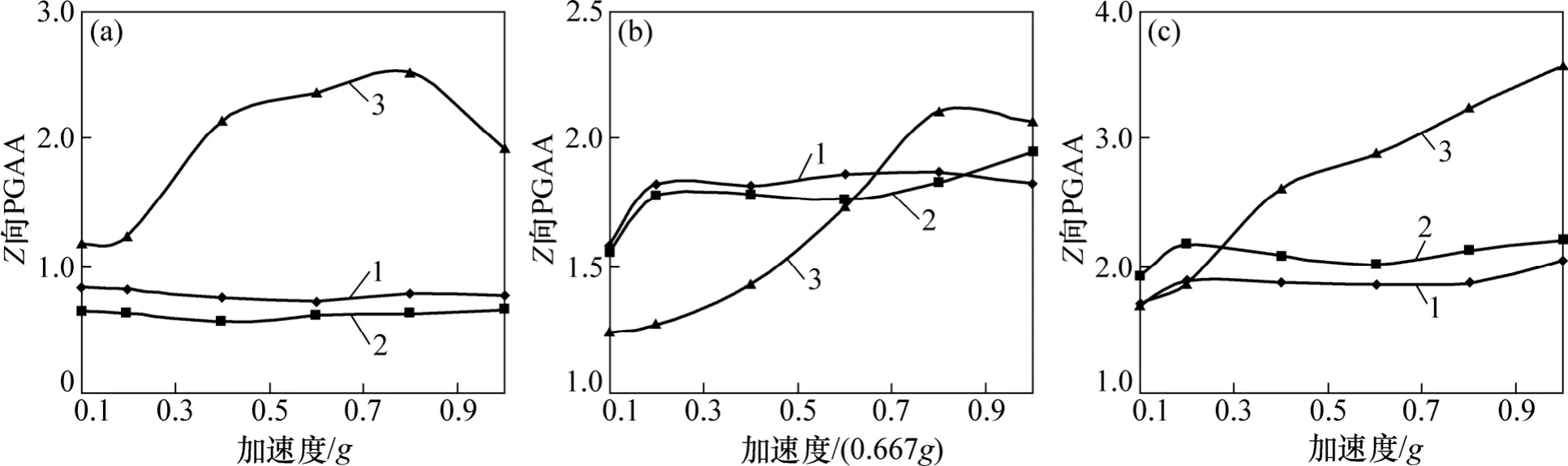
圖9 護坡Z向PGAA隨激振加速度響應規律Fig.9 Response mechanism of Z-PGAA of lattice frame with peak exciting acceleration

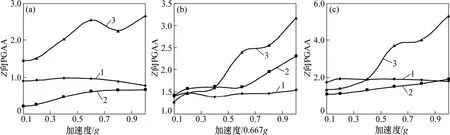
圖10 坡體Z向PGAA隨激振加速度響應規律Fig.10 Response mechanism of Z-PGAA in slope with peak exciting acceleration

圖11 護坡Z向PGAA隨坡高響應規律Fig.11 Response mechanism of Z-PGAA of lattice frame with slope height

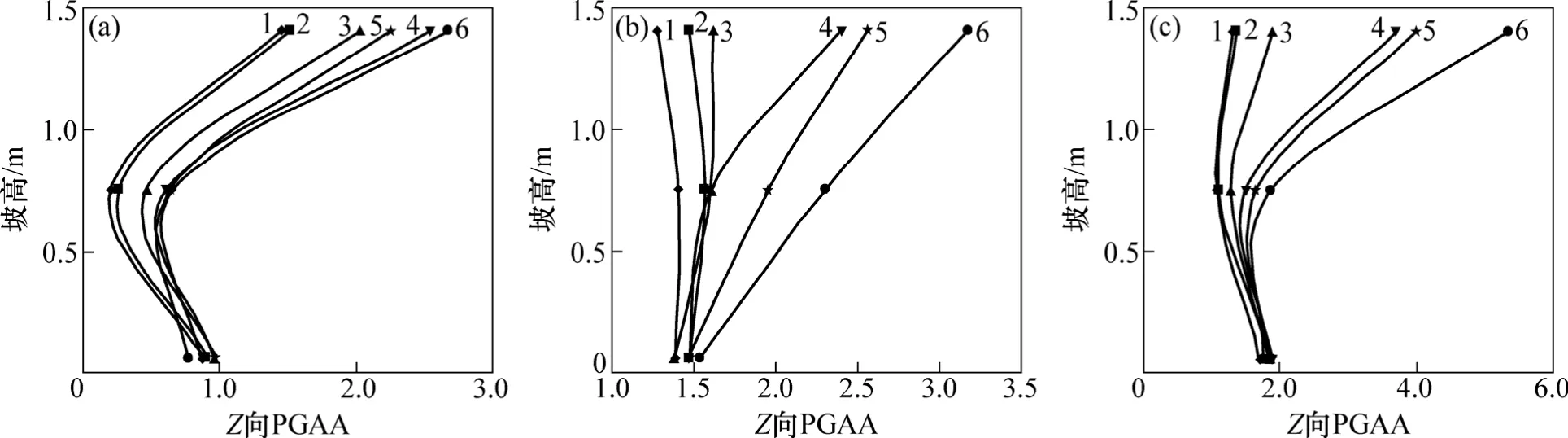
圖12 坡體Z向PGAA隨坡高響應規律Fig.12 Response mechanism of Z-PGAA in slope with slope height

在Z向激振下，邊坡Z向PGAA總體上隨激振加速度增大而增大。AZmax≥0.4g時邊坡上部坡內加速度動力響應強度比坡面的大；而對于中下部，坡內動力響應強度總體上比坡面的小。Z向PGAA隨坡高響應顯著且表現出非線性特征，其中AZmax≤0.267g時Z向PGAA隨坡高非線性減小，而 AZmax≥0.4g時 Z向PGAA隨坡高非線性增大。

在 XZ向激振下，豎直方向地震動力響應明顯，且比水平向動力響應程度顯著。Z向PGAA隨激振加速度非線性增大。坡內動力響應程度總體上比坡面的弱。高程對邊坡豎直方向地震動力響應明顯，表現出非線性特征，AXmax≥0.4g時Z向PGAA隨坡高而增大。

通過上述分析得出：模型邊坡 Z向加速度的放大主要是由于豎直方向地震波引起的。但是水平方向地震波會對邊坡上部豎直方向加速度產生較大的放大效應。

3 護坡動位移響應規律

3.1 護坡水平方向動位移響應規律

汶川波3種加載方式下，護坡各測點X向動位移響應規律如圖13和圖14所示。

從圖13～14可見：X向激振下，各測點動位移在激振加速度峰值 AXmax≤0.6g時響應值較小，AXmax≥0.8g時動位移響應幅度較大且永久位移急劇增大。

各測點的永久位移在AXmax≤0.6g時為負值，表明格構框架梁向土體外側移動；AXmax＞0.6g時都為正值，表明格構框架梁在水平方向向土體方向移動。

在Z向激振下，動位移響應幅度較小，且永久位移的量值很小，表明格構框架梁在X方向上的位移主要由X向激振波所產生。

XZ向激振下，各測點動位移在AXmax≤0.4g時響應值較小，AXmax≥0.6g時動位移響應幅度較大，永久位移逐漸增大且增大的幅度顯著。此時，各測點的動位移響應強度特性與X向激振時相同，但永久位移方向相反，表明護坡離開土體向外側移動，同時繞上端轉動。

試驗結果表明：動位移響應呈現出非線性特征[22]。這種特性不僅與激振加速度峰值有關，而且與測點位置、地震動方向和持續時間、端部約束等諸多因素有關。

3.2 護坡豎直方向動位移響應規律

汶川波3種加載方式下，護坡各測點Z向動位移響應規律如圖15和圖16所示。

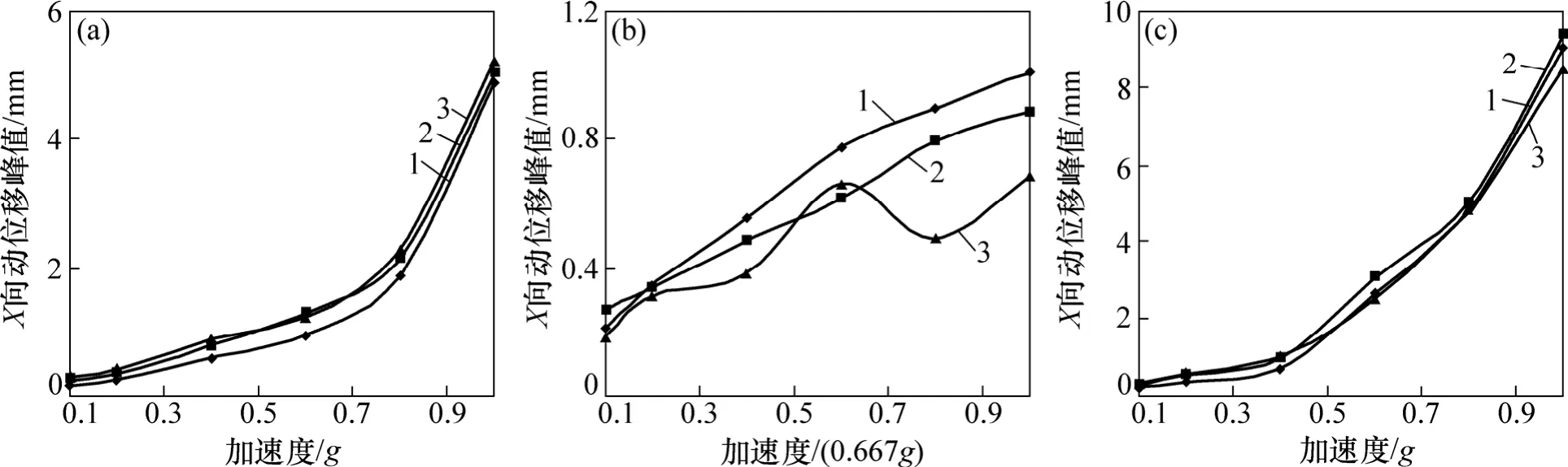
圖13 X向動位移峰值隨激振加速度響應規律Fig.13 Response mechanism of X peak displacement with peak exciting acceleration

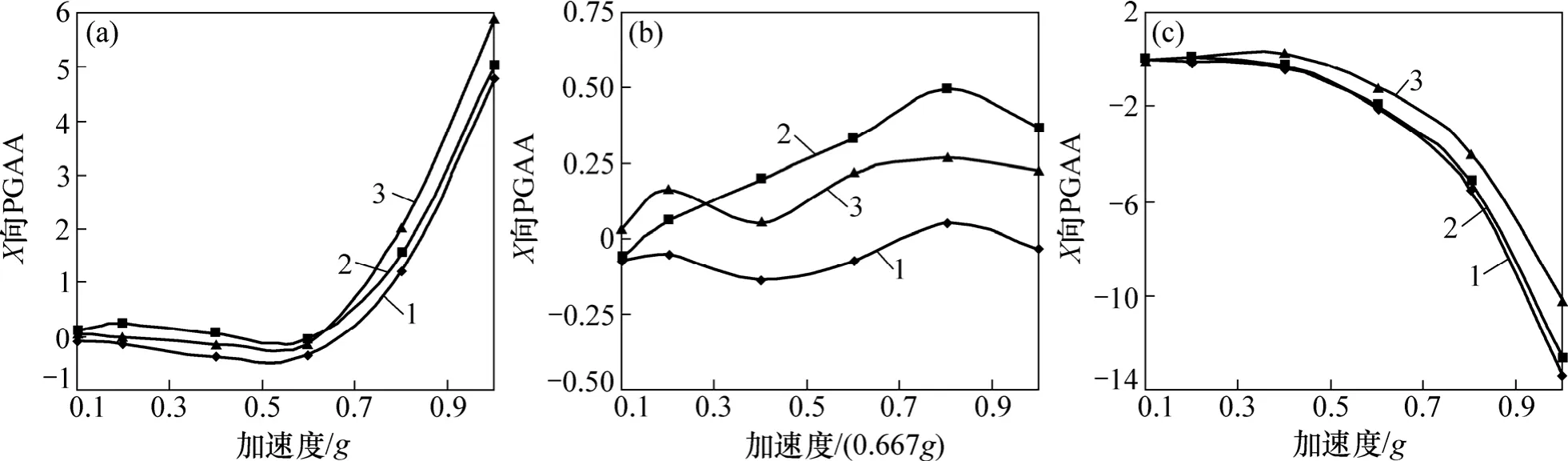
圖14 X向永久位移隨激振加速度響應規律Fig.14 Response mechanism of X permanent displacement with peak exciting acceleration

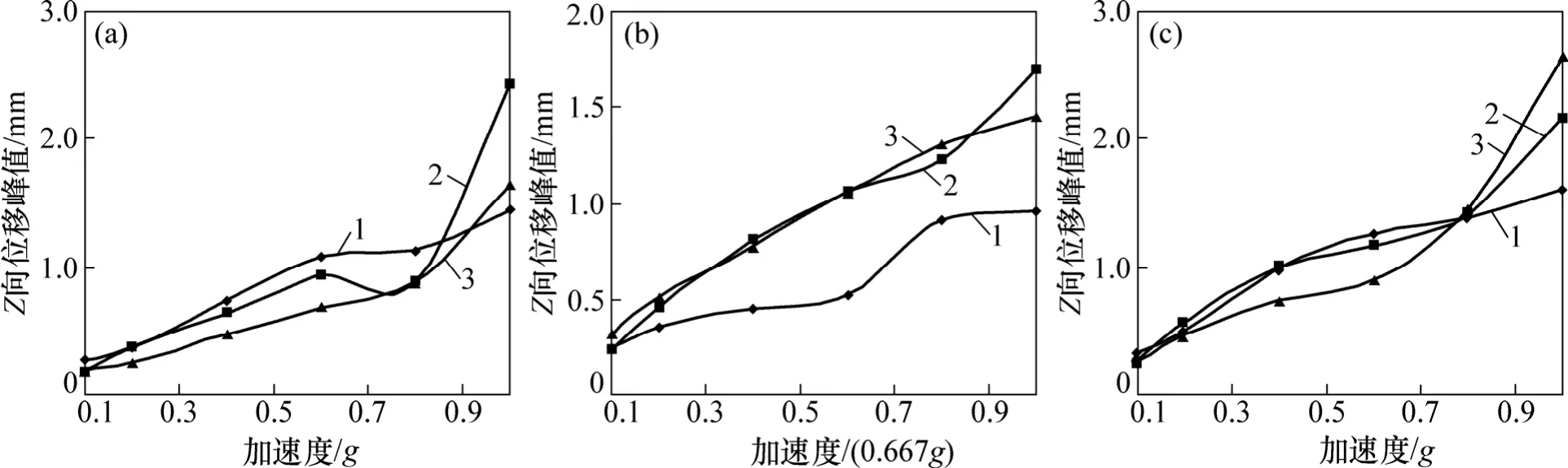
圖15 Z向動位移峰值隨激振加速度響應規律Fig.15 Response mechanism of Z peak displacement with peak exciting acceleration

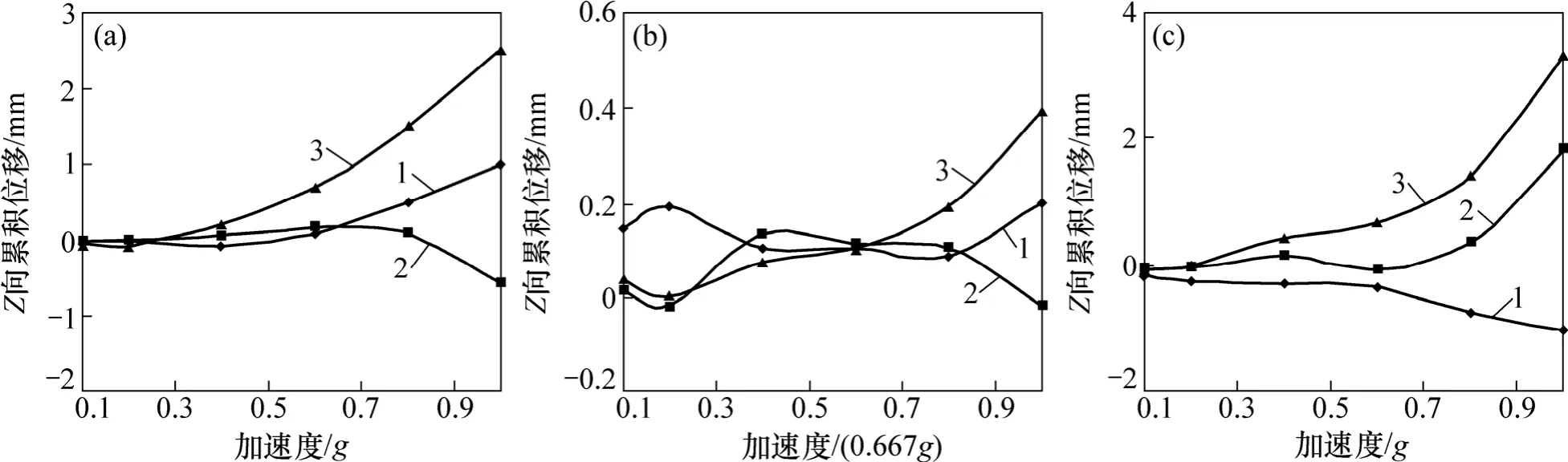
圖16 Z向永久位移隨激振加速度響應規律Fig.16 Response mechanism of Z permanent displacement with peak exciting acceleration

從圖15～16可見：在X向激振下，激振加速度峰值AXmax≤0.6g時各測點豎直方向永久位移較小。對測點永久位移數據分析表明：下端和上端向下移動，中部向上移動，發生彎曲變形。結合X方向的永久位移，格構框架梁發生向土體方向的平移，同時向邊坡下方移動。

在Z向激振下，各測點豎直向動位移響應幅度比X向單向激振時更小，且永久位移遠小于X向單向激振時的情形。因此，可以認為護坡Z向位移主要由水平方向的地震波所引起。

在XZ向激振下，動位移豎直向響應與X向單向激振時的情形相似。AXmax≤0.6g時，各測點豎直方向永久位移較小，但是，比X向單向激振時稍大。由于下端Z向永久位移為負值，中部和上部為正值，結合X向永久位移，說明格構框架梁在離開土體平移的同時繞上端轉動。

4 邊坡動土壓力響應規律

以激振加速度AXmax=0.6g時的動土壓力響應時程曲線(如圖17所示)為例，說明汶川波雙向激振時動土壓力響應規律。

汶川波有2個加速度幅值較大的時段，動土壓力響應隨之出現了2次突變，且第1次突變比第2次顯著。地震動使得邊坡產生殘余土壓力，其大小與測點位置、地震動強度等因素有關。當經歷了較強的地震動激振后，再經歷同樣大小的激振時殘余土壓力突變不顯著，這也就是第2次突變弱于第1次突變的原因。

各測點動土壓力隨激振加速度響應規律如圖 18所示，隨坡高的響應規律見圖19所示。

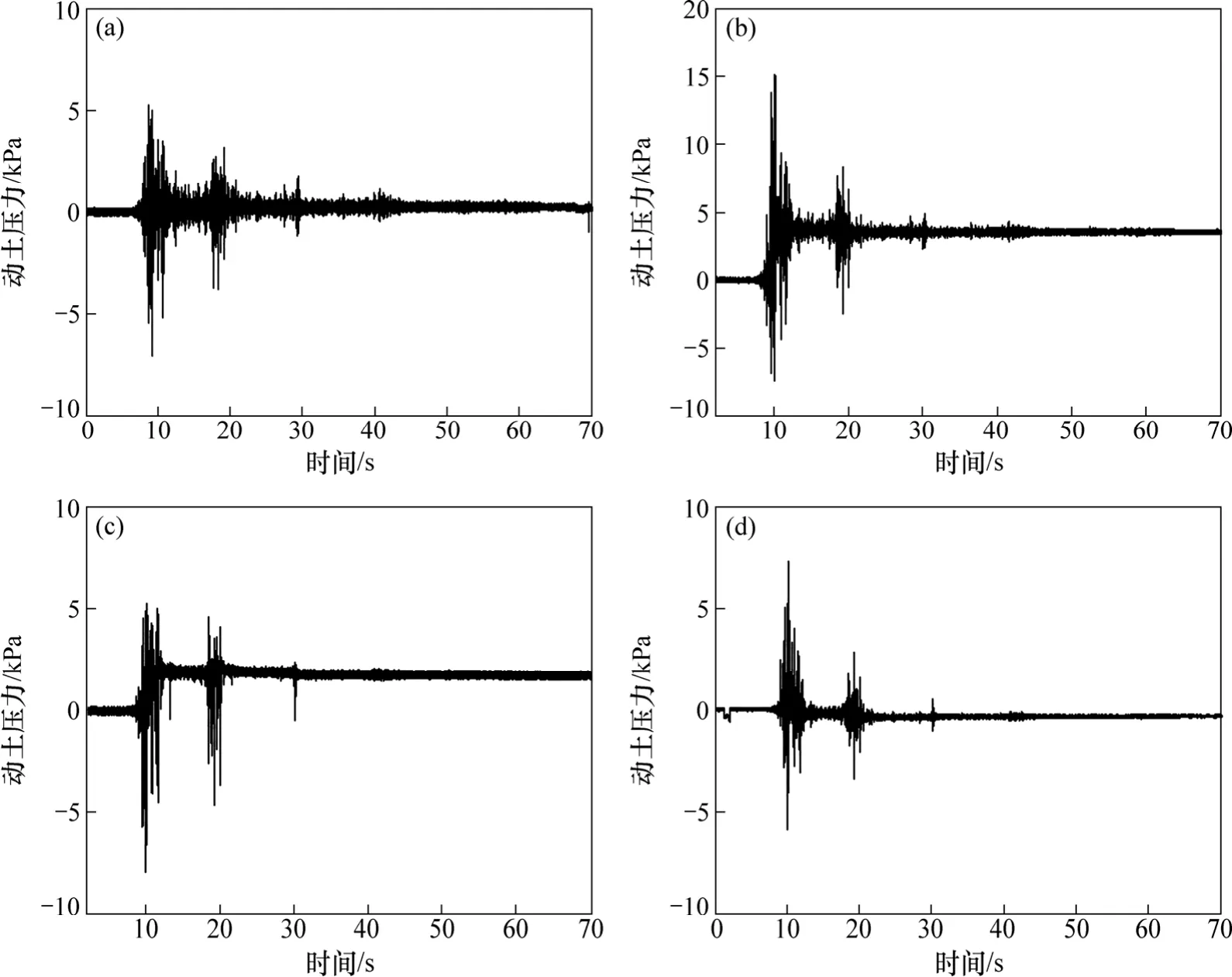
圖17 汶川波XZ雙向激振下(AXmax=0.6g)各測點動土壓力響應時程曲線Fig.17 Time-history of seismic earth pressure under XZ excitation (AXmax=0.6g)

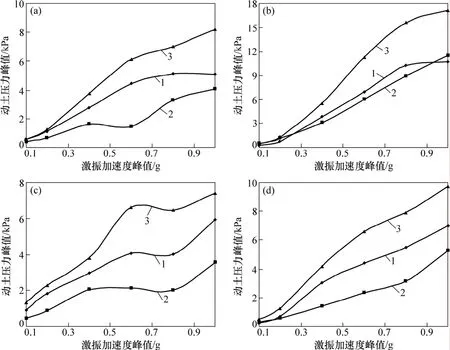
圖18 各測點動土壓力峰值隨汶川波激振加速度和激振方式變化情況Fig.18 Response mechanism of peak seismic earth pressure with peak exciting acceleration and directions

圖19 邊坡動土壓力在坡高上的響應規律Fig.19 Response mechanism of seismic earth pressure with slope height

從圖19可見：在汶川波X向、Z向或XZ雙向激振下，各測點動土壓力峰值總體上都隨激振波加速度的增大而增大；X向單向激振時各測點動土壓力峰值總體上比Z向單向激振時的稍大。

對FH2和FV2的數據分析表明：汶川波X單向或XZ雙向激振下，在激振加速度峰值AXmax≤0.4g時，水平方向和豎直方向動土壓力峰值較接近；當 AXmax＞0.4g時，水平方向動土壓力峰值遠大于豎直方向。在Z向單向激振下，水平方向動土壓力峰值同樣遠大于豎直方向動土壓力峰值。

從動土壓力在坡高上的響應特征看：無論是X向、Z向單向激振或XZ雙向激振下，動土壓力表現出非線性特征，當 AXmax≥0.4g(AZmax≥0.267g)時，動土壓力峰值的最大值都出現在坡中，呈現出兩頭小、中間大的非線性分布規律[23]。

5 結論

(1) 3種激振方式都使得邊坡產生水平和豎直向加速度動力響應，且這種動力響應及PGAA隨坡高變化都呈現出明顯的非線性特征。水平向激振主要產生水平方向加速度放大效應，邊坡上方響應強度比中下方明顯，內部響應強度比坡面明顯；豎直向激振主要產生豎直方向加速度放大效應，邊坡中上方坡內動力響應強度大于坡面，邊坡下方坡內動力響應強度稍弱于坡面；水平和豎直雙向激振時，水平向加速度動力響應特征是：強度明顯弱于豎直向；邊坡中下方PGAA隨激振加速度增大的變化幅度較小，隨坡高增大呈現出非線性增大；邊坡上部響應特征多變，如護坡X向PGAA除激振加速度峰值AXmax=0.6g增大外，其余情況下都隨坡高而減小；坡體X向PGAA除AXmax≤0.2g減小外，其余情況則是隨坡高而增大。豎直向加速度動力響應特征是AXmax≥0.4g時PGAA隨坡高非線性增大。

(2) 3種激振方式下動位移響應都呈現出非線性特征，水平方向動位移響應程度明顯比豎直方向的大，水平向的永久位移遠比豎直向的大，且豎直向激振時所產生的永久位移幾乎可以忽略不計。此外，在水平和豎直雙向激振時，水平向動位移響應程度比水平向單向激振時的強，且永久位移量值大但方向相反，豎直向永久位移與水平向單向激振時接近。

(3) 在 3種激振方式下，水平方向動土壓力響應程度比較接近；水平向動土壓力響應程度大于豎直方向動土壓力響應；水平方向動土壓力響應都呈現出兩頭小、中間大的非線性特征，即動土壓力峰值的最大值都出現在坡中。

[1]薛守義. 高等土力學[M]. 北京: 中國建材工業出版社, 2007:211-216.XUE Shou-yi. Advanced soil mechanics[M]. Beijing: China Building Materials Industry Press, 2007: 211-216.

[2]黃浩華. 地震模擬振動臺的設計與應用技術[M]. 北京: 地震出版社, 2008: 315-340.HUANG Hao-hua. The design and application technology on earthquake simulation vibrating table[M]. Beijing:Seismological Press, 2008: 315-340.

[3]孔憲京, 李永勝, 鄒德高, 等. 加筋邊坡振動臺模型試驗研究[J]. 水力發電學報, 2009, 28(5): 152-157.KONG Xian-jing, LI Yong-sheng, ZOU De-gao, et al. Shaking table model tests on soil slope reinforced with geo-grid[J].Journal of Hydroelectric Engineering, 2009, 28(5): 152-157.

[4]Tinawi R, Leger P, Leclerc M, et al. Seismic safety of gravity dams: from shake table experiments to numerical analyses[J].Journal of Structural Engineering, 2000(4): 518-529.

[5]Lin M L, Wang K L. Seismic slope behavior in a large-scale shaking table model test[J]. Engineering Geology, 2006, 86:118-133.

[6]Li Q S, Li Z N, Li G Q, et al. Experimental and numerical seismic investigations of the Three Gorges dam[J]. Engineering Structures, 2005, 27(4): 501-513.

[7]Pitilakis D, Dietz M, Wood D M, et al. Numerical simulation of dynamic soil–structure interaction in shaking table testing[J].Soil Dynamics and Earthquake Engineering, 2008, 28(6):453-467.

[8]Anastasopoulos I, Georgarakos T, Georgiannou V, et al. Seismic performance of bar-mat reinforced-soil retaining wall: Shaking table testing versus numerical analysis with modified kinematic hardening constitutive model[J]. Soil Dynamics and Earthquake Engineering, 2010, 30(10): 1089-1105.

[9]Lee K Z Z, Chang N Y, Ko H Y. Numerical simulation of geosynthetic-reinforced soil walls under seismic shaking[J].Geotextiles and Geomembranes, 2010, 28(4): 317-334.

[10]劉小生, 王鐘寧, 汪小剛, 等. 面板壩大型振動臺模型試驗與動力分析[M]. 北京: 中國水利水電出版社, 2005: 9-20.LIU Xiao-sheng, WANG Zhong-ning, WANG Xiao-gang, et al.Large scale shaking table model tests and dynamic analysis of concrete face rockfill dam[M]. Beijing: China Water Power Press,2005: 9-20.

[11]林皋, 朱彤, 林蓓. 結構動力模型試驗的相似技巧[J]. 大連理工大學學報, 2000, 40(1): 1-8.LIN Gao, ZHU Tong, LIN Bei. Similarity technique for dynamic structural model test[J]. Journal of Dalian University of Technology, 2000, 40(1): 1-8.

[12]Iai, Susumu. Similitude for shaking table tests on soil-structure-fluid model in 1-g gravitational field[J]. Soils and Foundations, 1989, 29(1): 105-118.

[13]GB 5001—2001, 建筑抗震設計規范[S].GB 5001—2001, Code for seismic design of buildings[S].

[14]GB 50111—2006, 鐵路工程抗震設計規范[S].GB 50111—2006, Code for seismic design of railway engineering[S].

[15]周靖, 陳凱亮, 羅高杰. 速度脈沖型地震地面運動強度表征參數評估[J]. 振動與沖擊, 2010, 29(7): 153-158.ZHOU Jing, CHEN Kai-liang, LUO Gao-jie. Evaluation of intensity measures for pulse-like earthquake ground motions[J].Journal of Vibration and Shock, 2010, 29(7): 153-158.

[16]陳躍慶, 呂西林, 李培振, 等. 不同土性的地基-結構動力相互作用振動臺模型試驗對比研究[J]. 土木工程學報, 2006,39(5): 57-64.CHEN Yue-qing, LU Xi-lin, LI Pei-zhen, et al. Comparative study on the dynamic soil-structure interaction system with various soils by using shaking table model tests[J]. China Civil Engineering Journal, 2006, 39(5): 57-64.

[17]許強, 劉漢香, 鄒威, 等. 斜坡加速度動力響應特性的大型振動臺試驗研究[J]. 巖石力學與工程學報, 2010, 29(12):2420-2428.XU Qiang, LIU Han-xiang, ZOU Wei, et al. Large-scale shaking table test study of acceleration dynamic response characteristics of slopes[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(12): 2420-2428.

[18]陳強, 楊長衛, 張建經, 等. “5.12”汶川地震中高大加筋土擋墻破壞機理研究[J]. 鐵道建筑, 2010(9): 73-77.CHEN Qiang, YANG Chang-wei, ZHANG Jian-jing, et al. Study on damage mechanics of high reinforced earth retaining wall under “5.12” Wenchuan Earthquake[J]. Railway Construction,2010, (9): 73-77.

[19]徐光興, 姚令侃, 高召寧, 等. 邊坡動力特性與動力響應的大型振動臺模型試驗研究[J]. 巖石力學與工程學報, 2008, 27(3):624-632.XU Guang-xing, YAO Ling-kan, GAO Zhao-ning, et al.Large-scale shaking table model test study on dynamic characteristics and dynamic responses of slope[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(3):624-632.

[20]李昀, 楊果林, 林宇亮. 水平地震作用下綠色加筋格賓擋土墻動力特性試驗研究[J]. 中南大學學報: 自然科學版, 2010,41(1): 347-352.LI Yun, YANG Guo-lin, LIN Yu-liang. Dynamic characteristics of green reinforced gabion walls subjected to horizontal seismic loading[J]. Journal of Central South University: Science and Technology, 2010, 41(1): 347-352.

[21]欒茂田, 李湛, 范慶來. 土石壩擬靜力抗震穩定性分析與壩坡地震滑移量估算[J]. 巖土力學, 2007, 28(2): 224-230.LUAN Mao-tian, LI Zhan, FAN Qing-lai. Analysis and evaluation of pseudo-static aseismic stability and seism-induced sliding movement of earth-rock dams[J]. Rock and Soil Mechanics, 2007, 28(2): 224-230.

[22]Kramer S L, Smith M W. Modified Newmark model for seismic displacements of compliant slopes[J]. Journal of Geotechnical and Geoenvironmental Engineering, ASCE, 1997, 123(7):635-644.

[23]林彤. 離心模型試驗在超高加筋土擋墻中的應用研究[J]. 土木工程學報, 2004, 37(2): 43-46.LIN Tong. Study on the application of centrifuge modeling test to super-elevation reinforced earth retaining wall[J]. China Civil Engineering Journal, 2004, 37(2): 43-46.