基于Excel三次樣條函數的求解

張遠雙

（武漢船舶職業技術學院，湖北武漢 430050）

在計算機輔助船舶設計和建造中，三次樣條函數是船體型線典型的數學表達。在平面直角坐標系xoy中，給定若干個型值點Pi（xi，yi）（i＝0，1，2，…，n），船體型線可用三次樣條函數描述為［1］：

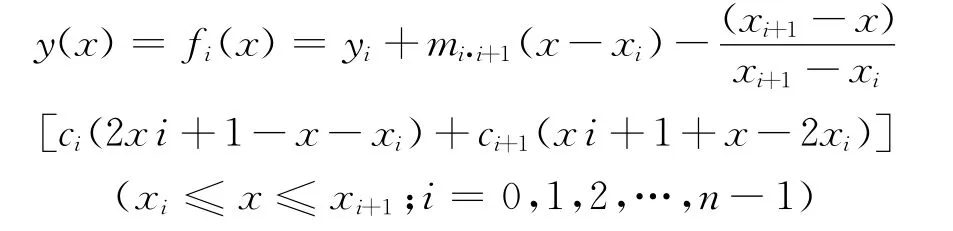
式中：mi·i＋1為一階差商；

ci為三次樣條函數的系數，根據節點關系式和端點條件，系數ci的求解表達式可表示為：

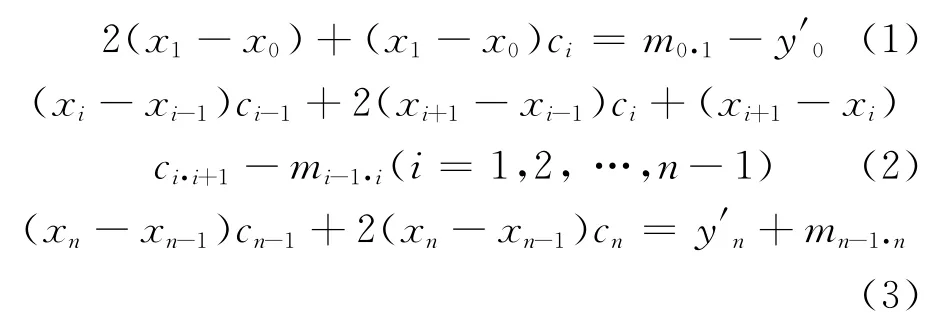
用三次樣條函數描述船體型線的關鍵在于求解三次樣條函數的系數。

1 線性方程組求解方法分析

系數ci的表達式（1）、（2）、（3）可化為n元一次方程組，根據數學知識將線性方程組改寫成矩陣方程AX＝B，系數方陣A為平行于對角線的三列稀疏矩陣，若其逆陣存在（即系數行列式的值不為零），則方程組有唯一解X＝A－1B。

用常規追趕法［2］求解上述n元一次線性方程組，隨n值的增大，求解過程愈復雜，具有相當難度。Excel是目前非常流行且計算功能強大的電子表格軟件，使用Excel的規劃求解工具或函數功能求解方程組可大大提高工作效率、保證求解精度。現以150t冷藏船3500WL為例，說明基于Excel系數ci求解的方法和過程。根據船體型線圖，已知條件如表1所示。

表1 型值和端點條件

2 用Excel的規劃求解工具求解

2.1 準備計算

為更好地使用Excel求解線性方程組，先進行一階差商mi·i＋1和線性方程組增廣矩陣的計算。

（1）一階差商的計算

一階差商mi·i＋1的計算表達式為：mi·i＋1＝利用相關Excel公式求得各一階差商大小如表2所示。

表2 差商m值的計算

（2）線性方程組增廣矩陣的計算

根據三次樣條函數系數ci的表達式，利用相關Excel公式求得線性方程組的增廣矩陣如表3所示，其中A9：K19單元格區域為系數矩陣，A9：L19單元格區域為增廣矩陣。

本例系數行列式的Excel計算公式可表達為“＝MDETERM（A9：K19）”，經計算其值為6.956×1045。根據克萊姆法則，該三次樣條函數系數線性方程組有唯一解。

在系數ci的求解表達式（1）、（2）、（3）中，將方程等號右邊的常數項移至左邊，能使左邊多項式的值為零時的ci值即為線性方程組的解。

2.2 “規劃求解”命令宏的加載和設置

在默認狀態下，Excel的【工具】菜單中無【規劃求解】選項。加載方法：單擊【工具】菜單的【加載宏】選項，在彈出的【加載宏】對話框中選中【規劃求解】選項，單擊【確定】按鈕。

打開【規劃求解選項】對話框，根據求解需要設置【最長運算時間】、【迭代次數】、【精度】、【允許誤差】和【收斂度】等選項。

2.3 用規劃求解工具求解樣條函數系數［3］

如表4、5所示，B21：B31單元格區域用于存放系數的計算結果；C21：C31單元格區域中的各單元格計算公式分別設置為“＝A9＊B21＋B9＊B22－L9”、“＝A10＊B21＋B10＊B22＋C10＊B23－L10”、…和“＝J19＊B30＋K19＊B31－L19”，用于表示方程組左邊多項式的值，規劃求解前多項式的值如表4所示。

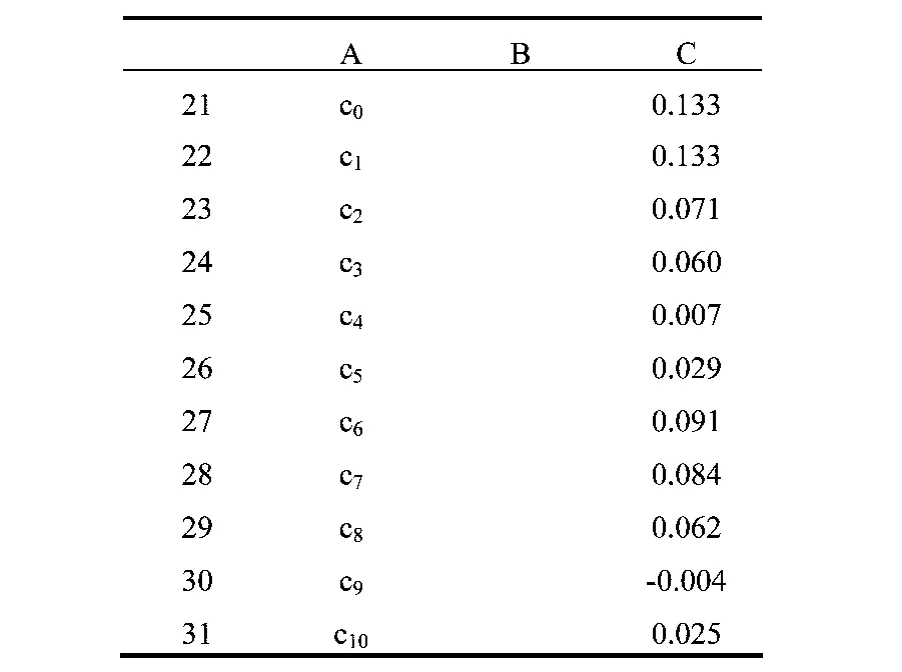
表4 規劃求解（1）

單擊【工具】菜單中的【規劃求解】選項，彈出【規劃求解參數】對話框，正確設置【設置目標單元格】、【等于】、【可變單元格】和【約束】等項目，如圖1所示，再單擊【求解】按鈕；在彈出的【規劃求解結果】對話框中，選取【保存規劃求解結果】，最后單擊【確定】按鈕。

經規劃求解，三次樣條函數系數的計算結果如表5中的B21：B31單元格區域所示。注意：目標單元格的值和約束條件的設置必須保證各多項式的值為零。

圖1 規劃求解參數的設置

表5 規劃求解（2）

3 用Excel的函數功能求解

一階差商mi·i＋1和線性方程組增廣矩陣的計算同2.1.1和2.1.2。可用MINVERSE和MMULT函數求系數矩陣的逆陣A－1和方程組的解X＝A－1B。

3.1 用MINVERSE函數求系數矩陣的逆陣

如表6所示，在Excel工作表中選定A33：K43單元格區域，插入函數 MINVERSE，打開MINVERSE函數對話框。

如圖2所示，在【函數參數】對話框中的“Array”參數文本框中選取A9：K19單元格區域作為計算逆陣的源數據區域，單擊【確定】按鈕，將光標定位在編輯欄中所插入函數的結尾處，同時按下組合鍵“Ctrl＋Shift＋Enter”，用數組公式“｛＝MINVERSE（A9：K19）｝”返回多個計算結果。A33：K43單元格區域顯示出逆陣的計算結果，在如表6所示。

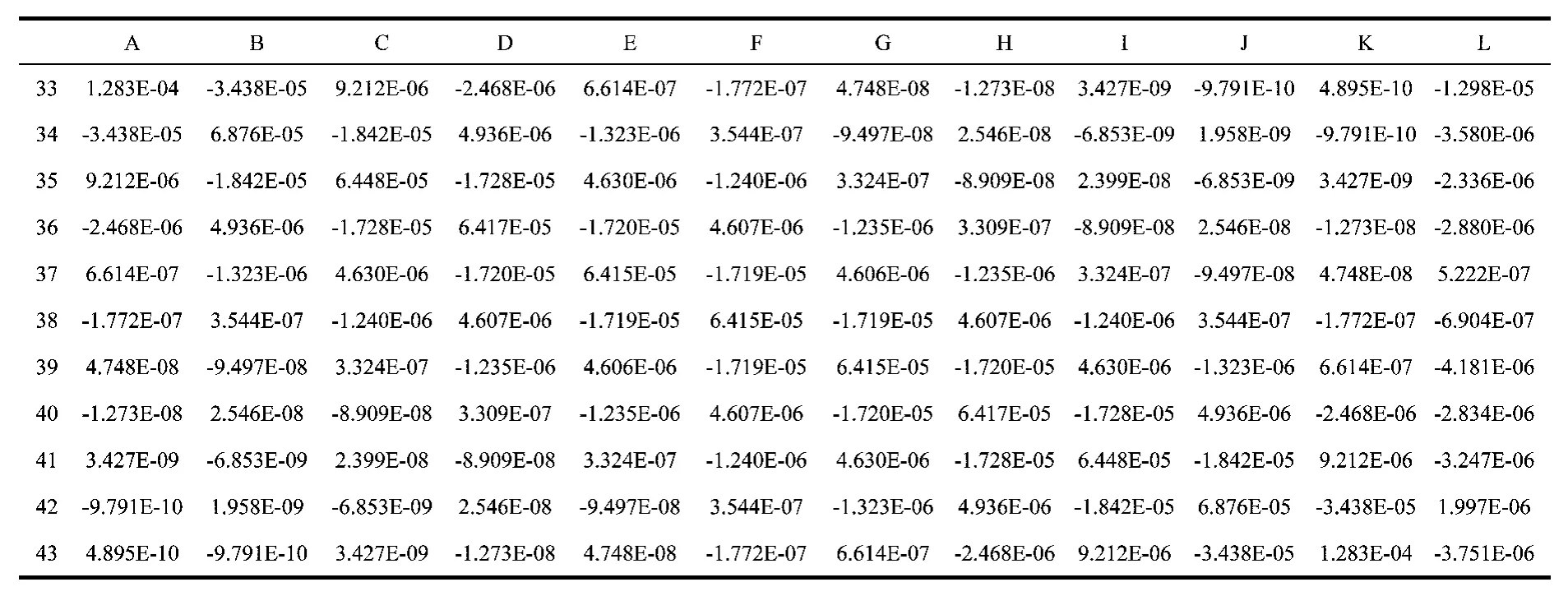
表6 系數矩陣逆陣的計算和方程組的求解

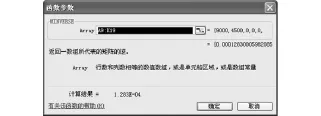
圖2 “MINVERSE”函數參數的設置

3.2 用MMULT函數求解樣條函數系數

如表6所示，在Excel工作表中選定L33：L43單元格區域，插入函數 MMULT，打開MMULT函數對話框。

如圖3所示，在【函數參數】對話框中的“Array1”和“Array2”參數文本框中分別選取A33：K43和L9：L19單元格區域作為計算系數ci的源數據區域，單擊【確定】按鈕，將光標定位在編輯欄中所插入公式的結尾處，同時按下組合鍵“Ctrl＋Shift＋Enter”，用數組公式“｛＝MMULT（A33：K43，L9：L19）｝”計算出系數ci的計算結果，如表6所示中L33：L43單元格區域所示。

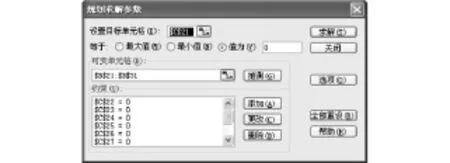
圖3 “MMULT”函數參數的設置

討論：本例亦可利用Excel的 MDETERM函數，根據克萊姆法則［4］進行求解（求解方法和過程略）。

4 結 語

在無相關專業軟件的情況下，三次樣條函數的求解是一個非常復雜且難以求解的專業問題，用Excel的規劃求解工具和函數功能進行計算，不僅能實現復雜問題的簡單化處理，大大提高求解效率，同時具有計算模型通用性強、計算過程簡明、計算結果準確等優點。

1 徐兆康.船舶建造工藝學［M］.人民交通出版社，2000：50～54.

2 王勇毅.計算機輔助船體建造［M］.人民交通出版社，1995：41～43.

3 謝國鋒等.Excel 2000中文版入門提高［M］.清華大學出版社，2000：281～285.

4 同濟大學數學教研室.線性代數［M］.高等教育出版社，1991：21.