基于多小波基的聯合圖像去噪方法*

劉美華,劉慧

(1.湖南工程學院 工程訓練中心,湖南 湘潭 411104;2.湖南師范大學 物理與信息科學學院,湖南 長沙410081)

小波分析在圖像處理中有著廣泛的應用，近年來，基于小波閾值的圖像去噪主要是使用單個小波變換對圖像進行處理。小波變換的一個特點是小波基的多樣性。選擇使用多個小波基來處理圖像,既保持了單小波的諸多優點,又克服了其缺陷，而且可以把小波十分重要的光滑性、緊支性、正交性、對稱性等完美地結合起來。在圖像處理中，這些特性具有很重要的作用。正交性對信號或者圖像重構獲得較好的平滑效果非常有用。對稱性能夠避免移相。與緊支小波相對應的濾波器是有限脈沖響應FIR(Finite Impulse Response)濾波器，它能使得相應的快速小波變換之和是有限的。光滑性對壓縮有著重要作用，因為如果小波不光滑，變換帶來的誤差很容易由視覺檢測出來。將這些優點結合在一起，使用多個小波基分別對含噪圖像進行處理得到多幅重構圖像，然后對這些圖像進行算術平均，得到最終去噪圖像。

1 小波閾值去噪

1.1 閾值求法

1992年，Donoho和Johnstone提出了小波閾值收縮方法(Wave Shrink)，此法在最小均方誤差意義下可達近似最優，且能取得較好的視覺效果，因而得到了深入研究和廣泛應用。目前已提出了多種閾值選取方法，有DJ閾值、Sure閾值、Penalized閾值和 Bayesian閾值方法[1-4]。DJ閾值依賴于采樣點數目,而且數量通常過大。因為采用的是單一閾值，所以會造成各自的去噪不平衡。Sure閾值是一種基于Stein無偏/似然估計原理的自適應閾值。給定一個閾值t，得到它的似然估計，再將非似然t最小化就可得到所選閾值[5]。該方法是一種軟閾值估計器。Bayesian閾值是通過 Bayesian似然估計最小化推導出來的，取得了較好的實驗效果。

本文采用Penalized閾值中的Birge-Massart懲罰函數方法，由小波系數選擇規則得到。閾值由極小化的懲罰規則得到[6]：

其中,c(k)是小波系數，按照絕對值遞減的順序存儲;σ是噪聲的標準差;α是調整參數，其值越大，降噪圖像的小波表示越稀疏，其典型值為2；n是小波系數的個數。設tmin是式(1)的極小值，那么閾值 T=|c(tmin)|。

1.2 閾值函數選擇

閾值化處理有軟閾值函數(Soft Threshold)與硬閾值函數(Hard Threshold)兩種[7]。其中軟閾值函數為:

硬閾值函數為：

其中，t是小波系數，T是閾值。軟閾值函數是將小波系數t與閾值T進行比較，然后根據比較的結果再向0收縮。硬閾值是使絕對值大于T的小波系數保留，其他置零。

通過實驗可知,在高斯噪聲水平低時，硬閾值去噪效果(以峰值信噪比為參考)一般優于軟閾值。在噪聲水平達到臨界值(58 dB)以上時，軟閾值去噪效果優于硬閾值。本文測試所加的噪聲水平范圍在5 dB～25 dB之間,因此采用硬閾值函數處理[8]。

2 小波基的選擇

現有的小波基函數主要分為半正交小波、正交小波、雙正交小波等幾類[9],常用的小波有 Daubechies正交小波系、基于B2樣條函數構造的雙正交小波系、Mexh小波、Meyer小波等。不同小波基去噪效果與噪聲水平、圖像的特點等具體情況有關[10]。對于噪聲來說,在正交小波基下分解系數的分布范圍比在雙正交小波基下的分布范圍小。因而當噪聲水平低時,正交小波分解所保留的高頻系數對重構去噪圖像的貢獻要比雙正交小波分解的貢獻大；當噪聲水平比較高時，由于雙正交小波分解系數分布的范圍比正交小波分解的范圍大，在大的閾值下所保留下來的系數含原圖像能量較多[11]。選擇小波基時,一般應選擇不同系列、不同緊支集長度的小波基。數目越多，去噪效果越好，但計算量大、處理時間長,一般來說選3～5個小波基即可。本文選用sym13、coif5和dmey 3個小波基聯合進行圖像去噪。

3 算法步驟

多小波基聯合去噪的算法步驟如下。

(1)分別對原始圖像使用 sym13、coif5和 dmey 3個小波基作J次分解，本文選取J=2;

(2)針對每個小波基分解后的圖像高頻系數進行硬閾值處理，閾值由式(1)極小值得到;

(3)使用 sym13、coif5和 dmey 3個小波基分別進行圖像重構，得到三幅重構圖;

(4)將這三幅重構圖進行算術平均,得到最終去噪圖像。

4 實驗結果

選用 512×512的 lena圖和 232×205的 tire圖來進行實驗。仿真環境為Matlab 7.0。分別對兩幅圖像加入噪聲水平為 5 dB、10 dB、15 dB、20 dB、25 dB 的高斯白噪聲,用MSE(均方誤差)和PSNR(峰值信噪比)來進行客觀評價：

表1和表2分別給出了在各種噪聲條件下應用單一小波基去噪和應用多小波基去噪的lena和tire圖像的均方誤差和峰值信噪比結果。

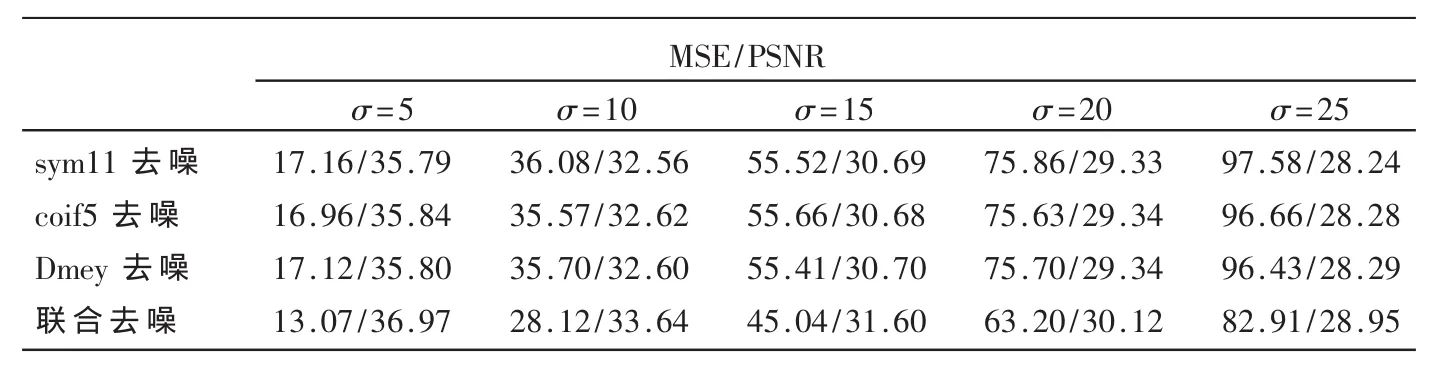
表1 單一小波去噪及多小波聯合去噪lena圖像的MSE及PSNR對比表

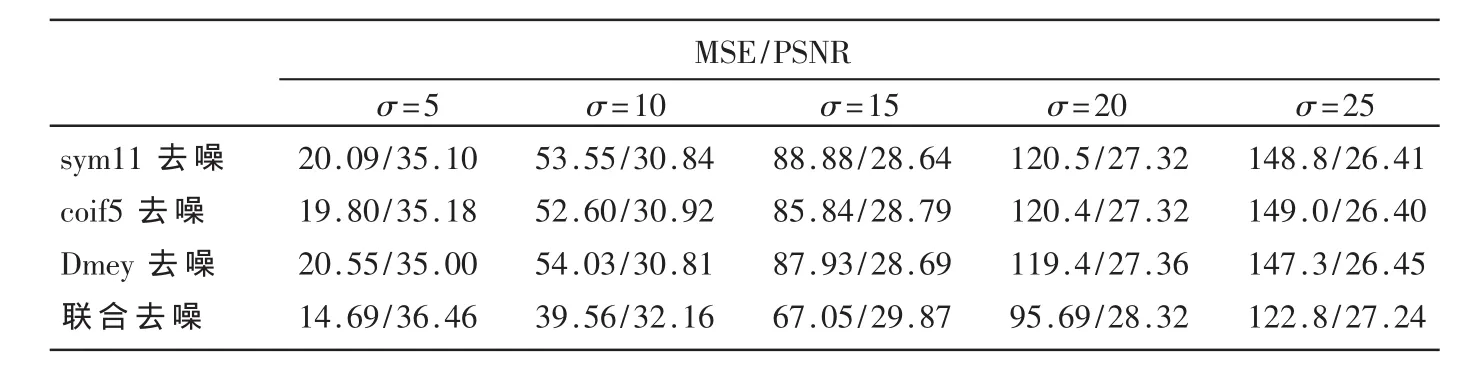
表2 單一小波去噪及多小波聯合去噪tire圖像的MSE及PSNR對比表

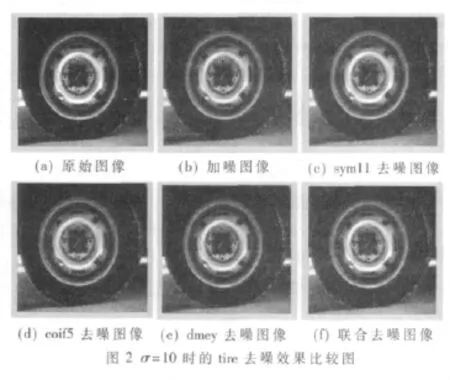
鑒于篇幅，只列出 σ=25時 lena和 σ=10時 tire的去噪效果比較圖，如圖1和圖2所示

從實驗結果可以看出，應用sym11、coif5和 dmey三個小波基聯合去噪的結果比分別用這3個單小波去噪有絕對的優勢。

從實驗結果可以看出,采用Birge-Massart懲罰函數閾值方法進行多小波基聯合去噪比單小波去噪在效果上大有改善。應用單小波分別對閾值去噪重構之后的圖像進行算術平均處理，得到的最終圖像的峰值信噪比只應用單個小波提高許多。此法綜合了各小波基的優點，且算法簡單，容易實現。

[1]劉守山,楊辰龍,李凌,等.基于自適應小波閾值的超聲信號消噪[J].浙江大學學報(理學版),2007,41(9):1557-1560.

[2]CHANG S G,Yu Bin,VETTERLI M.Adaptive wavelet thresholding for image denoising and compression[J].IEEE Transactions on Image Processing,2000,9(9):1532-1546.

[3]PORTILLA J,STRELA V,WAINWRIGHT M J,et al.Image denosing using scale mixtures of gaussians in the wavelet Domain[J].IEEE Transactions on Image Processing,2003,12(11):1338-1351.

[4]Zhang Wei,Yu Fei,Gao Hongmi.Improved adaptive wavelet threshold for image denoising[C].2009 Chinese Control and Decision Conference,2009:5958-5963.

[5]KAUR L,GUPTA S,CHAUHAN R C.Image denoising using wavelet thresholding[C].Indian Conference on Computer Vision,Graphics&Image Processing-ICVGIP,2002.

[6]飛思科技產品研發中心.小波分析理論與MATLAB7實現[M].北京:電子工業出版社，2005.

[7]孫延奎.小波分析及其應用[M].北京：機械工業出版社,2005.

[8]張磊,潘泉,張洪才,等.小波域濾波閾值參數 c的選取[J].電子學報,2001,29(3):400-402.

[9]蔡敦虎,羿旭明.小波基的選取對圖像去噪的影響[J].數學雜志,2005,25(2):185-190.

[10]李旭超,朱善安.小波域圖像降噪概述[J].中國圖象圖形學報,2006,11(9):1201-1209.

[11]費佩燕,郭寶龍.基于多小波的圖像去噪技術研究[J].中國圖象圖形學報,2005,10(1):107-112.