和值、平均遺漏值與理性購買體育彩票①
葉慧 何佳麗 張小皎
(江蘇科技大學數理學院 江蘇鎮江 212003)
隨著彩票的蓬勃發展,在帶來巨大經濟利益的同時,彩民在消費過程中也表現出一系列非理性行為。如:拼彩詐騙,高價收購中彩行賄,舉債十萬購彩,購彩洗黑等事件。前人在這方面的研究,大部分是從問卷角度得到數據,建立購彩模型;或從彩票出現的頻率分析彩票數字的概率為理性購彩提供借鑒。從和值和遺漏值出發,直接對彩票數字進行分析,可以省去在使用調查問卷數據時出現誤差的概率。本文通過網上隨機抽取100期11選5的數據,對非理性購彩行為特征、評價及其成因進行建模,得出其和值、平均遺漏值規律。本文的研究既為我國的管理者和研究者提供理論基礎同時也加強彩民的風險和法規意識。
1 理論貯備
1.1 和值和平均遺漏值得定義
和值就是所有號碼的和,一般在過濾中會用到。平均遺漏值是號碼有多少期沒有出現,而遺漏統計表則是對全部開獎號碼各種形態出現規律的一個全面統計。
1.2 擬合優度R2統計量
可用統計量R2來檢驗模型的擬合優度(1):
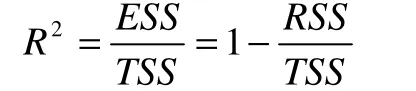
(Yi指樣本值,Y指的Yi平均值值擬的曲線的值,
TSS為總離差平方和(total sum of squares),反映樣本觀測值總體離差的大小;ESS為回歸平方和(explained sum of squarse),反映由模型中解釋變量所解釋的那部分離差的大小;RSS為殘差平方和(residual sum of squares),反映樣本觀測值與估計值偏離的大小,也是模型中解釋變量未解釋的那部分離差的大小。顯然,在總離平方和中,回歸平方和所占的比重越大,殘差平方和所占的比重越小,回歸直線與樣本點擬合得越好。統計量越接近于1,模型的擬合優度越高。如果模型與樣本完全擬合,則有R2=1。
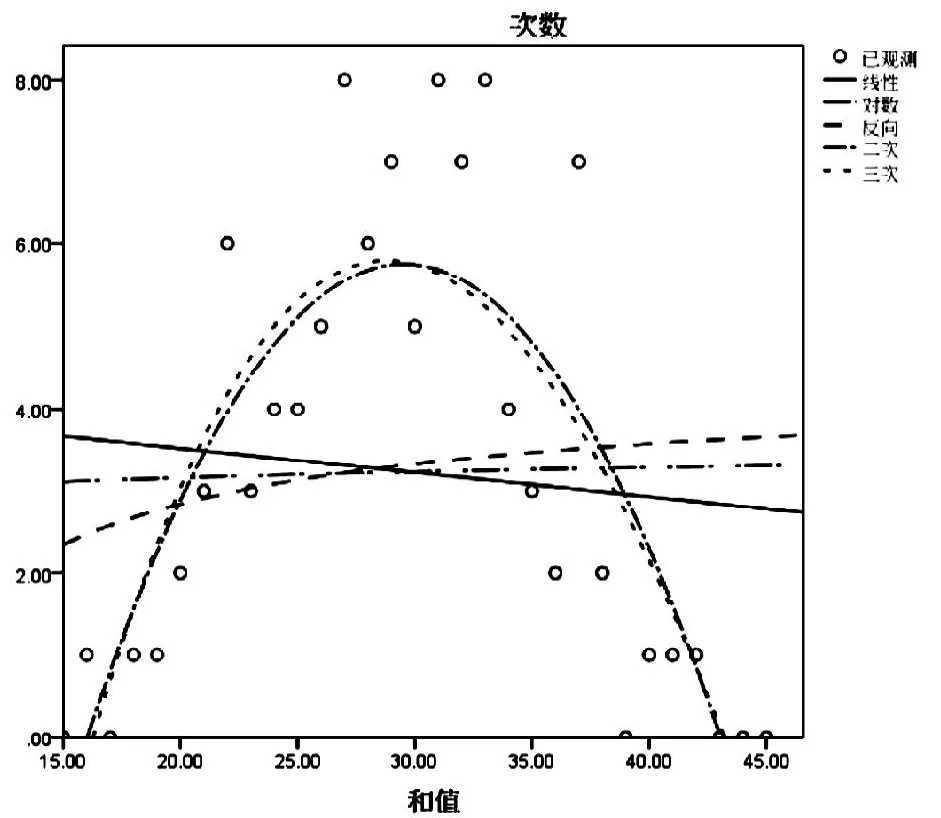
圖1 和值擬合曲線

圖2 平均遺漏值擬合曲線

表2 和值擬合方程
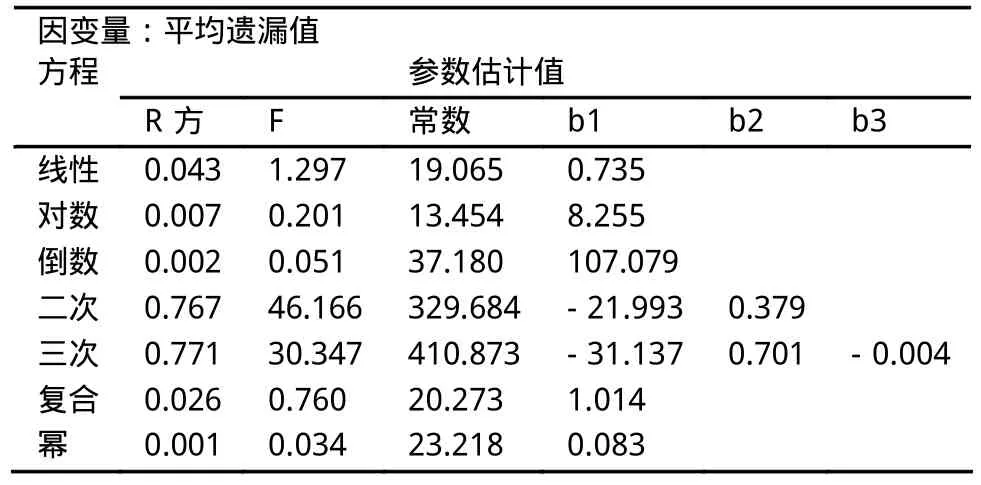
表3 平均遺漏值檢驗值
1.3 F檢驗
F檢驗是方差分析中的檢驗統計量。單因素方差分析的原假設是控制變量在不同水平下觀測變量各總體的均值無顯著差異。將F檢驗的值與查表得到的F表值比較,若F ≥ F表,表明控制變量在不同水平下觀測變量各總體的均值有顯著差異。
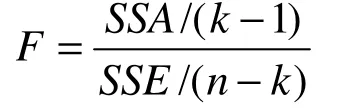
SST為觀測變量總離差平方和;SSA為組間離差平方和,是由控制變量的不同水平造成的變差;SSE為組內離差平方和,是由抽樣誤差引起的變差。n為總樣本量,k-1和n-k分別為SSA和SSE的自由度。
2 和值、平均遺漏值與理性購彩的聯系
從網上得到數據12011877期到12012012期的11選5的開獎結果(見附1體彩網站http://www.js-lottery.com/news/index.html)。計算出這一百期和值數據,據計量經濟學的理論知識,當擬合度R2達到0.6,F檢驗較大,可認為方程是合理的。為計算出合理的方程,用SPSS軟件進行多種函數的和值擬合方程(見圖1)。
由圖1及公式(1)、(2)得到下面的檢驗值表。

表4 平均遺漏值擬合方程
從表1中的參數可得出5個形式不同的方程(見表2)。
由表1和表2得到,運用二次方程擬合出來的曲線的擬合度達到0.687,F檢驗為30.787。運用三次方程擬合出來的曲線的擬合度為0.692,F檢驗為20.240。由于兩者擬合度相差不大,但是二次方程F檢驗的值明顯大于三次方程,據計量經濟學知識知,選取二次方程較好。即(3):
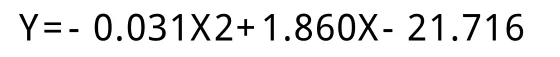
雖然該擬合優度沒有達到0.8的高度擬合程度,但已是非常接近,所以方程(1)可信。因此彩民通過對二次函數峰值上對的和值的數值來購買彩票。
為了進一步驗證二次方程的可信程度,用SPSS軟件進行多種函數平均遺漏值的擬合方程與曲線,得到圖2。
由圖2及公式(1)、(2)得到下面的檢驗值表3。
從表3中的參數可得出5個形式不同的方程(見表4)。
由表3和表4得知,二次方程擬合出來的曲線的擬合度達到0.767,F檢驗為46.166。運用三次方程擬合出來的曲線的擬合度為0.771,F檢驗為30.347。由于兩者擬合度相差不大,但是二次方程F檢驗的值明顯大于三次方程,所以選取二次方程較好。由上表得二次方程為(4):
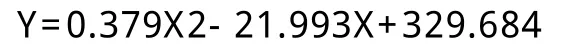
雖然該擬合優度沒有達到0.8的高度擬合程度,但是已經是非常接近,所以認為該方程可信。上述兩部分分析可得,和值出現在25到35直接較多,并且彩民可以根據號碼的遺漏值來大約確定本期和值為多少。
3 結語
運用SPSS對網上數據進行和值、平均遺漏值的擬合,據R方和F檢驗值得出最優的擬合方程,提高理性購彩。
[1]薛薇.統計分析與SPSS的應用[M].中國人民出版社,2011.
[2]楊東鋒.對山西省體育彩票消費者的調查分析[J].中北大學學報(社會科學版),2008,24(4).
[3]馮百鳴.中國彩票業發展極不平衡 彩民年人均購彩超千元[J].中國經濟周刊,2010.

