聲納浮標網絡目標定位算法研究＊

周兆軍

（海軍702廠 上海 200434)

1 引言

聲納浮標網絡是由大量的聲納浮標利用無線傳感器網絡（WSN)技術［1～3］組成的一個自組織網絡系統。聲納浮標網絡可用于對潛艇等水下目標進行定位，由于其利用多個節點相互協同，實現對目標的定位，因此其定位精度遠遠高于單個浮標定位精度。為了減少通信量，提高目標定位的實時性，聲納浮標往往只探測目標是否在自身探測范圍內，所以其屬于二元傳感器，即傳感器探測值只有0和1。所以聲納浮標網絡屬于二元傳感器網絡。

國內外對二元傳感器網絡目標定位與跟蹤也進行了相應的研究［4～6］。文獻［4～5］主要采用質心算法及加權質心算法來對目標進行定位。質心算法當傳感器的探測范圍較小時具有較好的性能，但當傳感器的探測范圍較大時，其性能大大降低。文獻［5］的幾種加權算法的權值都沒有有效體現節點到目標的距離，因此精度不是很高。文獻［6］提出了距離加權質心定位算法，使各個節點的權重有效體現了節點到目標的距離，提高了目標定位精度。但是各節點卻需要傳送額外的距離信息到融合中心，因此通信量增大，失去了二元傳感器網絡通信量小的優勢。

本文針對文獻［6］的不足，提出一種新的時間加權質心算法。算法將各節點探測的信號強度轉換成節點發送探測信息的等待時間，利用等待時間的長短對各個節點位置進行加權，因此權重體現了各節點到目標的距離，提高了定位精度。由于不需要傳送距離信息，因此通信量與質心算法相同。

2 問題描述

2.1 網絡模型

WSN由N個聲納浮標節點組成，所有節點以均勻概率密度隨機布設在網絡監測區域內。假設每個節點都有唯一的標識且都知道自身的位置。每個浮標節點具有一定的無線通信距離C和探測距離R。其中，通信距離C由節點的無線通信功率決定，探測距離R由浮標節點的探測模型決定。在無線通信距離內，浮標節點之間可以通過無線方式進行通信，且每個節點都知道其鄰居節點（距離小于通信距離)的位置。另外，浮標的通信距離C大于等于探測距離R的二倍，從而保證能夠探測到目標的節點間都能夠相互通信。最后，假設所有的浮標節點嚴格時間同步。

2.2 浮標探測模型

浮標節點探測目標的聲音信號強度，并進行本地處理以得到節點的探測值。假設在時刻t，目標的位置為lt，節點s的位置為rs，則時刻t浮標節點s探測到的來自目標的信號強度［8～9］為

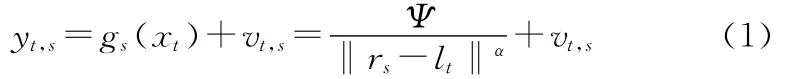
其中Ψ為單位距離上測得的來自目標的信號強度；‖rslt‖為rs和lt之間的歐幾里德距離。α為損耗因子，它由信號的傳播介質決定。可以認為它是一直不變的，并且對于所有浮標節點是相等的。vt，s為t時刻節點s接收到的噪聲強度，當用于求平均能量的時間窗長度T足夠長時，可以認為其服從于均值為uv、方差為σ2v的正態分布，即vt，s～N（uv，δ2v)。

節點在探測到來自目標的信號強度以后，在本地進行處理，并根據以下的規則決定其探測值。

1)節點將實際測得的信號強度與一個預定的閾值γ比較，如果測得的值小于γ，則其探測值為0。

2)如果測得的信號強度大于γ，則其探測值為1。

由上述模型的定義可得浮標節點的觀測方程如下：

其中ys為節點測得的信號強度，可由式（1)得到。

在浮標節點獲得探測值后，如果其探測值為0，則節點不向融合中心發送任何信息，以節省能量，如果探測值為1，則向融合中心發送信息。

3 時間加權質心算法

3.1 質心算法

質心算法的基本思想是：某一時刻如果有多個傳感器節點探測到目標，則以這些探測到目標的節點的幾何中心作為該時刻目標的位置。

3.2 距離加權質心算法

針對傳統的質心算法和加權質心算法的不足，文獻［6］提出了距離加權質心算法，其基本思想為：節點在測得目標信號強度后，根據傳感器的探測模型，利用信號強度求出節點到目標的距離，然后將距離和探測信息一起發往融合中心，融合中心利用各節點到目標的距離對各節點的位置進行加權得到目標的位置。即如果某一時刻有S個節點探測到目標，其位置分別為（x1，y1)，（x2，y2)，…，（xS，yS)，且各節點到目標的距離分別為d1，d2，…，dS，則目標的位置為

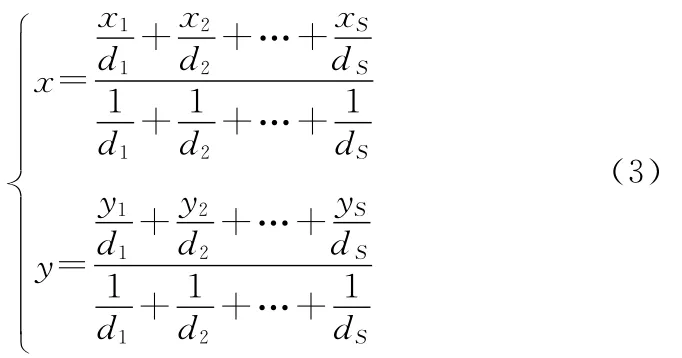
這種距離加權質心算法雖然使各個節點的權重有效體現了節點到目標的距離，提高了目標定位和跟蹤精度。但是各節點卻需要傳送額外的距離信息到融合中心，因此通信量增大，失去了二元傳感器網絡通信量小的優勢

3.3 時間加權質心算法

為了克服距離加權質心算法的不足，我們提出時間加權質心算法。其基本思想為：將各個節點探測到的信號強度轉換成節點發送其探測信息的等待時間，從而每個探測到目標的節點發送信息的等待時間中就包含了節點到目標的距離，然后融合中心可以利用各節點的等待時間對各節點位置進行加權。下面進行詳細介紹。

每一采樣時刻，當浮標節點發現目標后，首先為該節點設置一等待時間ζs，當等待時間ζs結束后，節點再將探測信息傳送給融合中心。其中ζs跟節點探測到的目標信號強度成反比，即ζs可以定義為

其中γ為探測閾值，ζmax為最大等待時間，由節點的采樣間隔和目標速度決定。由于是單跳通信，因此通信時間很短，假設可以忽略不計。另外，由于所有節點是嚴格時間同步的，因此各節點傳送探測信息的等待時間中就反映了該節點探測到的目標信號強度，從而也反映了該節點到目標的距離。因此，融合中心可以利用各節點發送信息的等待時間來對各節點的位置進行加權，在不增加通信量的情況下，提高質心算法的定位精度。

由浮標節點探測模型式（1)可得

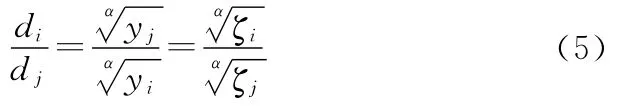
故，式（3)的距離加權質心算法可以等價為時間加權質心算法：

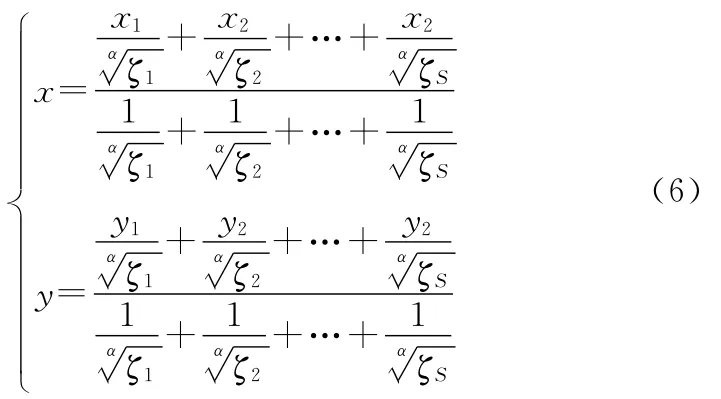
由于時間加權質心算法同樣只傳送節點的二元探測值到融合中心，因此其通信量與質心算法完全一樣，不會增加額外的能耗。

4 計算機仿真分析

為了驗證時間加權質心算法的有效性，利用Monte Carlo仿真［10～11］，將時間加權質心算法與質心算法的性能進行比較。仿真環境設置如下：

假設N個浮標節點以均勻概率密度隨機布設在200×200m2的監測區域內，坐標原點設在網絡覆蓋區域的左下角。所有浮標節點的采樣周期Tperiod＝1s，單位距離上測得的來自目標的信號強度Ψ＝1000，損耗因子α＝2，所有浮標節點的探測閾值為γ，系統狀態噪聲為Qw＝diag｛［0.01，0.01］｝，觀測噪聲均值為uv＝0，方差為δv＝0.09。

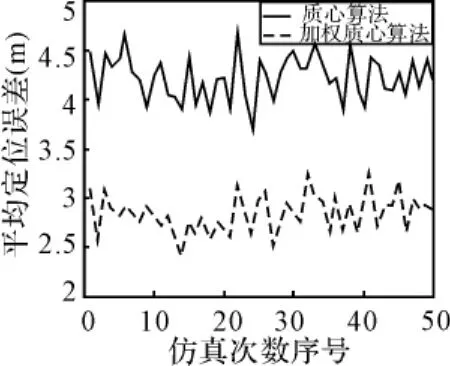
圖1 兩種算法定位精度比較

首先對算法的定位精度進行比較。仿真參數設置為：節點個數N＝400，探測閾值γ＝2。仿真50次，每次仿真中隨機產生100個目標位置點，分別利用質心算法和時間加權質心算法對目標進行定位，并計算出每種定位方法的平均定位距離誤差。仿真結果如圖1所示。

從仿真結果可以看出，時間加權質心算法的平均定位誤差明顯小于質心算法的平均定位誤差。以所有定位誤差的均值來計算，時間加權質心算法相比質心算法定位精度可提高32.89%。

另外，為了驗證節點個數N、節點探測閾值γ等參數對定位精度的影響，分別做了兩次Monte Carlo仿真：1)假定節點探測閾值γ＝2，節點個數N從200變化到600，仿真結果如圖2所示；2)假定節點個數為N＝400，節點探測閾值γ從2變化到5，仿真結果如圖3所示。

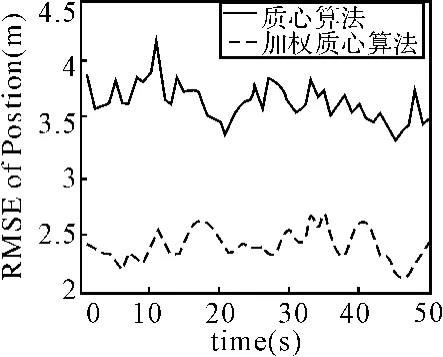
圖2 節點個數對定位精度的影響

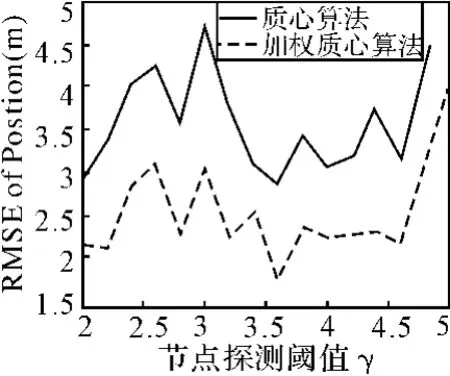
圖3 節點探測閾值γ對定位精度的影響

從仿真結果可以看出，質心算法和加權質心算法的定位誤差都隨著節點數目的增加而減小，而與探測閾值γ的關系不是很大。由于時間加權質心算法和質心算法的通信量完全相同，因此其能耗也與質心算法相同。

5 結語

聲納浮標網絡可用于對潛艇等水下目標進行定位，因此其具有重要的軍事應用價值。本文針對已有距離加權質心算法的不足，提出了一種新的時間加權質心定位算法，在通信量與質心算法一樣的情況下提高了目標定位精度。新的時間加權質心算法將各個節點探測的信號強度轉換成節點發送探測信息的等待時間，利用等待時間的長短對各個節點位置進行加權，因此權重體現了各節點到目標的距離，提高了目標定位與跟蹤精度，而通信量與質心算法相同。仿真結果表明驗證了算法的有效性。下一步我們將研究節點部署策略對定位跟蹤精度的影響。

［1］CheeYee Chong，Kumar S P.Sensor networks：evolution，opportunities，and challenges［J］.Proc.of the IEEE，2003，91（8)：1247–1256.

［2］Li D，Wong K D，Hu Y H，et al.Detection，Classification，and Tracking of Targets［J］.IEEE Signal Processing Magazine，2002，19（2)：1729.

［3］Chong CY，Kumar S P.Sensor Netwoks：Evoltion，Opportunities，and Challenges［C］.Proceedings of the IEEE，2003，91（8)：12471256.

［4］Mechitov K，Sundresh S，Kwon Y，et al.Cooperative Tracking with Binary Detection Sensor Networks［C］.Proceedings of 1st International Conference on Embedded Networked Sensor Systems，2003：332333.

［5］Djuric P M，Vemula M，Bugallo M F.Target Tracking by Particle Filtering in Binary Sensor Networks［J］.IEEE Transactions on Signal Processing，2008，56（6)：22292238.

［6］孫曉艷，李建東，陳彥輝，等.二進制傳感器網絡加權目標跟蹤算法研究［J］.電子與信息學報，2010，32（9)：20522057.

［7］彭燕.無線傳感器網絡定位優化算法及其仿真［J］.計算機與數字工程，2011（3).

［8］SHENG Xiao Hong，Hu YH.Maximum Likelihood Multiplesource Localization Using Acoustic Energy Measurements with Wireless Sensor Networks［J］.Transactions on Signal Processing，2005，53（1)：4453.

［9］Hu YH，SHENG Xiao Hong.Dynamc Sensor SelfOrganization for distributive Moving Target Tracking［J］.Journal of Signal Processing Systems，2008，51（1)：161171.

［10］Liu J S，Chen Rong.SequentialMonte Carlo Methods for Dynamic Systems［J］.Journal of Americal Statistical Association，1998，93（443)：10321044.

［11］Bortz A B.Kalos M H，Lebowitz J L.A new Algorithm for Monte Carlo Simulation of Ising Spin Systems［J］.Journal of Computational Physics，1975，17（1)：1018.