無結構動態適應無線傳感器網絡數據融合算法

樂俊，張維明，肖衛東，湯大權，唐九陽

（國防科學技術大學 信息系統工程重點實驗室，湖南 長沙 410073）

1 引言

微機電系統、無線通信和數字電子等技術的發展促進了低成本、低功率和多功能傳感器的發展，這些傳感器由感知、數據處理和通信等模塊組成，尺寸小并可以進行短距離無線通信，將大量傳感器部署在監控區域，通過無線通信的方式相互連接，就可以組成無線傳感器網絡(WSN, wireless sensor networks)[1]。WSN一般包括大量傳感器節點（以下簡稱節點）和一個收集數據的基站，能夠實時監測、感知和采集網絡分布區域內的各種環境或監測對象信息，并對這些信息進行處理，然后傳送到需要這些信息的用戶。WSN不需要固定網絡支持，具有快速展開、抗毀性強等特點，可廣泛應用于軍事、工業、交通、環保等領域[2]。

在WSN的傳統應用中，網絡部署區域通常位于人無法輕易接近的遠程環境中，如森林、戰場、災難現場等場合，節點一般位于感知對象周邊，位置基本固定、電源不便更換，多個節點協同感知，基站往往位于網絡部署區域之外。隨著應用范圍的不斷擴展，尤其是物聯網的發展和應用，WSN的應用也出現了新的模式，網絡部署在日常環境如停車場、商場、倉庫中，更換節點電源相對可行，節點通常隨著物體移動，某個節點往往只負責感知其所對應物體及物體周圍環境的相關信息，基站位于網絡內部或邊緣。在這些新應用中，WSN具有網絡動態變化頻繁、對數據通信的可靠性要求高等特點。另一方面，WSN的一些本質特性在這些新應用中并沒有改變，由于節點體積受限、使用有限電源、采用無線通信方式等原因，節點的能量、通信距離和帶寬等資源都受到限制，所以，如何節約能量，提高通信效率仍然是需要面臨的問題。

數據融合是WSN解決資源受限問題所普遍采用的一種技術，它的基本思想是：當節點收到其他節點的數據后，不是分別轉發出去，而是對這些數據進行融合處理，將融合后的結果轉發出去，從而減少數據通信量[3]。在 WSN中，數據通信所消耗的能量要大大高于數據采集和數據處理所消耗的能量。所以，減少數據通信量就能夠有效降低能量的消耗，同時還能在一定程度上避免無線信道中的數據碰撞，從而提高通信效率。

在WSN新應用中，仍然可以采用數據融合節約能量和提高通信效率。本文針對WSN新應用中所出現的新需求，提出了一種無結構動態適應數據融合 (SFDA, structure-free and dynamic-adaptive data fusion) 算法，該算法不需要在傳感器之間建立和維護數據通信的結構、采用“多對多”的數據通信方式，以適應網絡的動態變化，提供高可靠性的數據通信。

2 相關工作

WSN中的數據融合就是在數據從節點向基站傳輸的過程中，由中間節點對來自多個節點的數據進行融合[4]。它需要完成2項工作：數據收集和融合處理。根據應用的不同，數據收集的方式可以分為事件觸發式、查詢式和周期性匯報式。融合處理則包括數據計算、數據分組合并或數據壓縮等方式。

現有的數據融合算法可以歸納為基于平面結構、基于分簇結構、基于樹狀結構、基于鏈路結構、基于混合結構和無結構幾大類。下面分別簡單介紹。

定向擴散(directed diffusion)[5]和 SPIN (sensor protocol for information via negotiation)[6]是基于平面結構算法的典型代表。在定向擴散算法中，基站周期性地向鄰近節點廣播興趣消息，興趣包括任務類型、目標區域、時間戳等參數。每個節點維護一個興趣列表，在接收到興趣消息后，將興趣的信息保存在興趣列表中，以建立該節點指向基站的梯度關系，并向鄰居節點轉發興趣消息。這樣，隨著興趣消息的轉發，每個收到興趣消息的節點都能建立起指向基站的梯度。當節點收集到與興趣相匹配的數據時，可以通過梯度信息將數據由其他節點依次轉發至基站。SPIN是一組基于協商的算法，節點在發送數據之前與其他節點進行協商，從而建立數據傳輸的路徑，然后再按路徑向基站發送數據。

LEACH(low energy adaptive clustering hierarchy)[7]是一種經典的基于分簇結構算法，它按照輪周期性運行，每輪都包括設置和穩定2個階段。在設置階段，節點以自組織的方式隨機選擇一定數目的簇首，然后，簇首廣播自己成為簇首的消息，其他節點依據接收該消息的信號強度選擇加入一個簇。在穩定階段，簇成員將數據發送至簇首，由簇首對數據進行融合處理后將結果發送至基站。很多分簇算法在LEACH的基礎上對簇首選擇方法和分簇的方式進行改進，例如，HEED(hybrid energyefficient distributed clustering)[8]在簇首選擇和分簇的過程中綜合考慮節點剩余能量和節點與鄰居節點的鄰近性或節點的度，使剩余能量較高的節點更有機會成為簇首，并能夠平衡簇間的負載。

基于樹狀結構算法通常以基站為根節點，將網絡中的節點組織成樹狀結構，數據沿著該結構向基站傳輸，并由非葉子節點進行數據的融合處理。這類算法的研究主要集中在如何建立樹狀結構方面，例如文獻[9]所提到的 3種方法：GIT(greedy incremental tree)、SPT(shortest paths tree)和 CNS(center at nearest source)。

基于鏈路結構算法的代表是PEGASIS (powerefficient gathering in sensor information systems)[10]，它將網絡中的所有節點連接成一條相鄰節點之間距離最短的鏈路，然后隨機選擇一個節點作為首領，從鏈路的兩端開始，節點依次向首領節點方向發送數據，中間節點將接收到的數據進行融合處理，并將融合結果發送至下一節點，最終由首領節點將數據發送至基站。

基于混合結構算法結合了上述結構中的2種或多種。例如，GSEN(group-based sensor network)[11]融合了分簇和鏈路2種結構，將每個簇內的節點構造成鏈路，簇首之間也形成高一級的鏈路，MLC(multi-level clusteirng)[12]則融合了分簇和樹狀 2種結構，在簇首和基站之間構造樹狀結構。

除了上述基于結構的數據融合算法外，也有文獻對無結構的數據融合算法進行了研究。文獻[13]針對事件觸發式數據收集，首次提出無結構數據融合算法，在該算法中，需要發送數據的節點采用任意多播機制將數據發送至某個可進行融合處理的節點。文獻[14]同樣針對事件觸發式數據收集，先動態選擇一些節點擔任融合節點，再由融合節點從其他節點收集數據進行融合后發送至基站。

3 相關模型及問題描述

3.1 網絡模型

網絡模型的建立是為了對算法的前提進行限定。假設WSN的部署區域是一個邊長為L、在二維坐標系中起始點（左下角頂點）坐標為(O_x,O_y)的二維正方形區域，節點均勻分布而且分布密度較大。除此之外，網絡還具有如下性質：1)基站位于網絡內部或邊緣、位置固定、坐標為(BS_x,BS_y)；2)所有節點都是同構的，節點可以通過定位設備或定位算法等方法獲得自己的位置信息；3)節點可以在網絡中移動或退出網絡，也可以有新的節點加入網絡；4)各節點以及基站之間時間同步；5)節點的通信距離可控，節點能夠根據通信距離調整發射功率；6)數據收集采用周期性匯報式，也就是說，每過一段時間，所有節點都向基站發送數據。

3.2 能耗模型

由于數據通信的能耗占傳感器節點總能耗的絕大部分，遠遠大于其他部分的能耗，因此，和同類算法一樣，本文只考慮數據傳輸和融合數據的能耗，節點獲得位置信息的能耗不考慮。

本文采用與LEACH相同的能耗模型，如果發送距離小于能耗模型閾值d0，采用自由空間模型，否則，采用多路徑衰減模型。節點發送和接收數據的能耗公式分別為

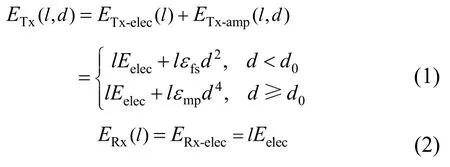
其中，l是數據的長度即比特數，d是數據發送距離，ETx-elec(l)是無線收發電路發送長度為 l的數據的電路能耗，ETx-amp(l,d)是將長度為l的數據發送至距離d的放大器能耗，Eelec是無線收發電路發送或接收單位長度數據的電路能耗，εfs和 εmp分別是自由空間模型和多路徑衰減模型的放大器能耗，ERx-elec(l)是無線收發電路接收長度為l的數據的電路能耗。

節點對k個長度為lbit的數據進行融合處理所需要消耗的能量為

其中，EDA是融合單位長度數據所需的能耗。

3.3 問題描述

與傳統應用相比，WSN的新應用尤其是其在物聯網中的應用具有一些新的特點，主要表現在以下2個方面。

1) 節點的動態加入或退出以及節點在網絡中的移動，導致網絡動態變化更加頻繁。傳感器往往附著在物體表面或安裝在物體內部，而這些物體往往具有較高的移動性。如果物體移動，傳感器就會隨之移動，物體從網絡之外進入網絡內、從網絡內移動至網絡外或者在網絡內的移動以及傳感器失效等都會造成網絡的變化。

2) 對數據通信的可靠性要求更高。在傳統應用中，多個節點協同工作，某些節點的數據傳輸失敗并不會對網絡的整體性能造成很大影響。而在新應用中，一個傳感器通常只負責感知和收集其所對應物體及物體周圍環境的相關信息。這就意味著，如果某個節點的數據無法傳送至基站，就無法獲得該節點對應物體的相關信息，從而產生不利的影響。

節點直接將數據發送至基站的方式雖然可以提高數據通信的可靠性，但是，由于節點的通信距離有限，網絡的規模和可擴展性都會受到限制，而采用泛洪的方法則會出現“信息爆炸”。上面所介紹的各類基于結構的數據融合算法也都不能滿足上述需求。首先，這些算法需要預先在節點之間構建某種結構，一個節點在發送數據之前需要與另外一個確定的節點建立連接，然后再按照該結構傳輸數據。而結構的建立需要節點間相互通信，節點會因為發送和接收控制消息而消耗較多的能量，如果采用固定的結構，必然無法適應網絡的動態變化，如果動態維護結構，就需要再花費額外的能量開銷；其次，基于結構的數據融合算法均采用“多對一”或者“一對一”的數據通信方式，傳輸路徑上存在一些關鍵節點，例如分簇結構中的簇首、樹狀結構中的非葉子節點以及鏈路結構中處于鏈路中間的節點等，如果這些節點失效，就會影響其他相關節點的數據傳輸。現有的無結構數據融合算法主要是針對事件觸發式數據收集，不適用于周期性匯報式數據收集，而且這些算法也采用“多對一”或者“一對一”的數據通信方式，同樣無法提供高可靠性的數據通信。

為了滿足這些新應用需求，本文針對周期性匯報式數據收集的無線傳感器網絡，提出SFDA這種新的數據融合算法，在實現數據融合以節約能耗和提高通信效率的同時，還能夠適應網絡的動態變化、保證高可靠性的數據通信。

4 SFDA算法設計

SFDA是一種無需在節點之間建立和維護結構、采用“多對多”數據通信方式的數據融合算法，它按輪運行，既可以按照固定的周期運行，也可以由基站隨時重新發起新的一輪，每輪包括設置階段和穩定階段。在設置階段，網絡被劃分為多個正方形柵格，各個節點確定自己所屬的柵格、傳輸數據的目的地和傳輸距離。在穩定階段，各個節點按照一定的時序發送數據，如果基站位于節點所屬柵格的鄰近柵格，節點就直接將數據發送至基站，其他柵格內的節點則從鄰近柵格中選擇一個作為下一跳目的地，一個柵格內的所有節點分別接收其上一跳柵格所有節點發送的數據并和自身的數據進行融合處理，再將融合結果發送至下一跳目的地，從而使節點的數據能夠通過一跳或多跳傳輸到達基站。

4.1 設置階段

在設置階段，首先由各個節點向基站發送自己的位置坐標、節點標識等相關信息，基站在收集完所有節點的信息后，就能夠獲得當前網絡的節點總數和節點分布信息，再結合節點可能失效的概率以及節點最大通信距離確定柵格的大小也就是柵格邊長，然后劃分柵格，確定每個柵格內節點的下一跳目的地，為每個柵格及柵格中的節點分配通信時隙。

柵格邊長是SFDA算法的一個參數，其取值由具體的應用決定，在同一應用中，每輪的柵格邊長也可以由基站動態確定。確定柵格邊長需要考慮 2個因素：一個是網絡的節點分布和動態性，必須使每個柵格中均分布有可參與數據通信的節點以提高數據通信的可靠性；一個是節點的通信距離，必須保證節點能夠完成下一跳數據傳輸。前一個條件要求柵格邊長不能小于某個值，也就是限定了柵格邊長的下界，后一個條件要求柵格邊長不能大于某個值，也就是限定了柵格邊長的上界。然后，可以在該下界和上界所確定的范圍內選擇一個合適的取值確定為柵格的邊長。

假設當前網絡中均勻分布有N個節點，需要確定的柵格邊長為B，則柵格的總數G為(L/B)2個，每個柵格中節點數目的期望值 NG為 N/G，每個節點失效的概率相同并設為PO，那么每個柵格可參與數據通信的節點（也就是有效節點）總數的期望值NT為

為了提高數據通信的可靠性，所以需要保證每個柵格中都分布著有效節點，也就是要求NT大于1，所以柵格邊長需要滿足：

另外，在數據通信時，一個柵格內的節點需要向鄰近某個柵格的所有節點發送數據，而節點與鄰近柵格節點最大距離的情況就是這2個節點分別位于2個柵格對角線的兩端，如圖1所示。設節點最大通信距離為R，則柵格邊長還應滿足：

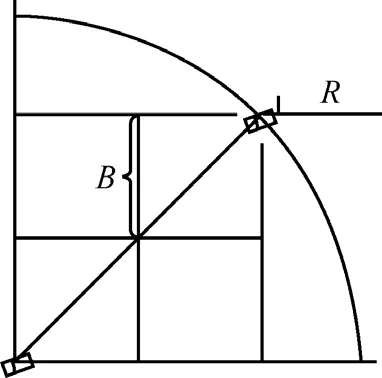
圖1 相鄰柵格節點最大距離示意

為了提高對網絡的動態適應性，算法基于網絡中節點的當前狀態和動態變化趨勢來預估其未來的狀態。需要說明的是，式(5)給出的柵格邊長下界是在節點均勻分布且分布密度較大以及每個節點失效概率均相等的條件下確定的，而式(6)給出的柵格邊長上界是在所有節點同構也就是最大通信距離相等的條件下確定的，因而，只要網絡能夠滿足上述條件，而且柵格邊長能夠同時滿足式(5)和式(6)，算法就可以保證每個柵格中都分布著有效節點而且節點能夠完成下一跳數據傳輸。在本文限定范圍之外的應用中，如果出現節點分布不均勻、節點失效概率不同或節點異構的情況，即使滿足式(5)和式(6)的柵格邊長也無法保證每個柵格中都分布著有效節點或節點能夠完成下一跳數據傳輸，針對這些情況，將在下一步工作中進行研究并分別提出相應的解決方案，擴展算法以提高算法的健壯性和擴大算法的應用范圍。還有，算法的性能如對網絡動態變化的適應能力和能量消耗都與柵格邊長的取值相關，未來，將通過定量的方法分析柵格邊長的最佳取值，以優化算法的性能。

基站的另一個工作是確定每個柵格內節點的下一跳目的地以及每個柵格和柵格內節點傳輸數據的時隙。首先給出幾個相關定義。

定義 1 （鄰近柵格）和某個柵格有公共邊或公共頂點的柵格稱為該柵格的鄰近柵格。

定義 2 （臨近柵格）基站位于內部或邊緣的柵格以及基站位于鄰近柵格內部或邊緣的柵格稱為臨近柵格。

定義 3 （臨近區域）所有臨近柵格組成的區域稱為臨近區域。

用二元組(G_x,G_y)作為柵格標識，其中，G_x是柵格橫標識，G_y是柵格縱標識，坐標為(x, y)的位置所處的柵格為，左下角柵格的標識為(1,1)、右上角柵格的標識為(L/B,L/B)，基站用(0,0)表示，基站所在柵格的標識為。臨近柵格和臨近區域的分布分為基站位于某個柵格頂點、邊界（不包括柵格頂點）或內部3種情況，如圖2所示，其中，五角星代表基站，陰影區域代表臨近區域。

圖2 臨近柵格和臨近區域示意

用[LB_x:RT_x,LB_y:RT_y]表示臨近區域，其中，LB_x和RT_x分別為左下角和右上角臨近柵格的橫標識，LB_y和RT_y分別為左下角和右上角臨近柵格的縱標識，可以通過算法1確定網絡的臨近區域。

算法1 確定臨近區域的算法偽碼

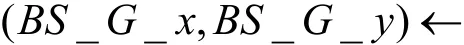
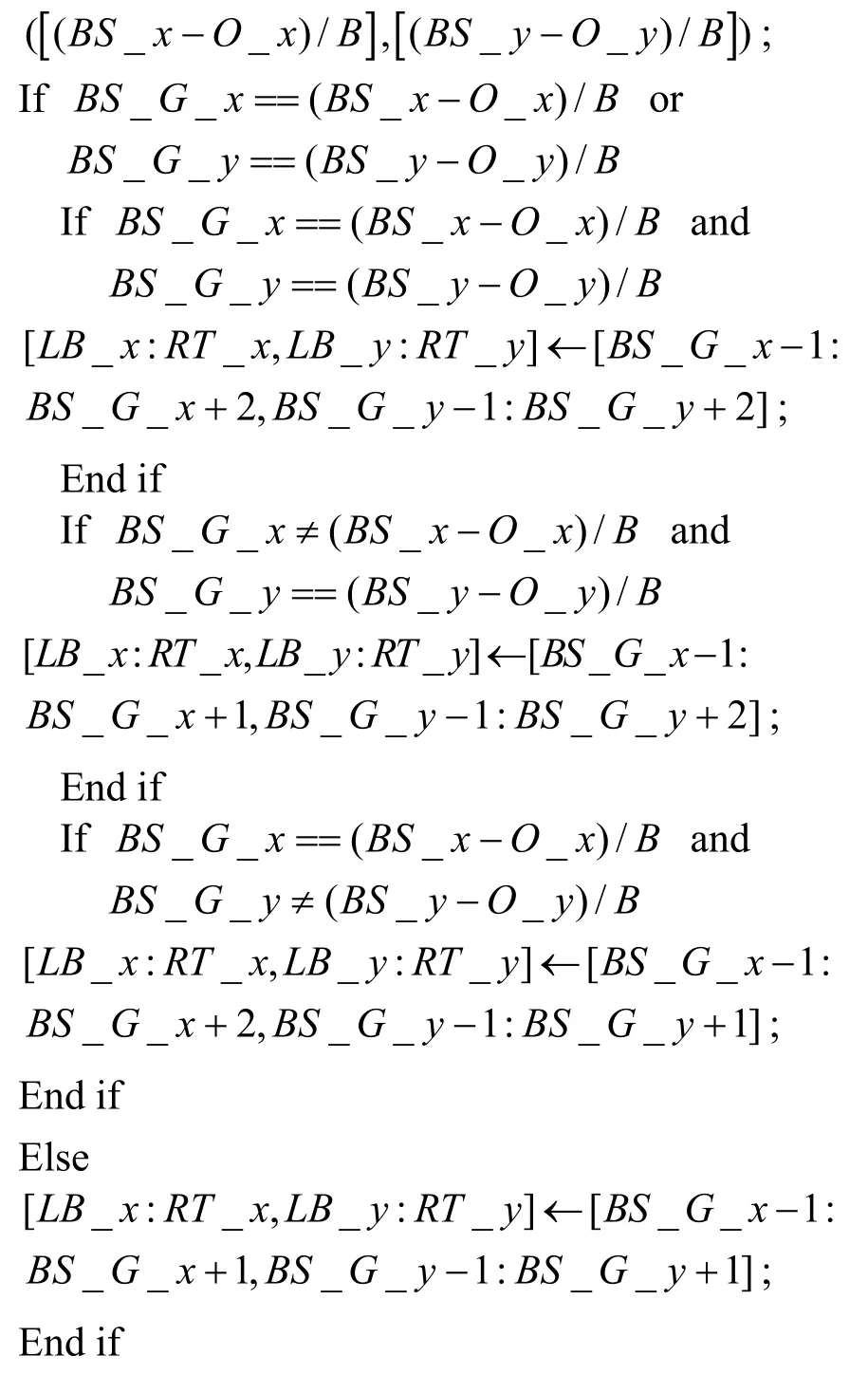
臨近柵格將基站作為目的地，其他柵格(G_x, G_y)選擇距離最近的臨近柵格(A_x,A_y)作為目的地，并從鄰近柵格中選擇一個柵格(N_x,N_y)作為下一跳，確定所有柵格目的地和下一跳的算法分別描述如下。

算法2 確定柵格目的地的算法偽碼

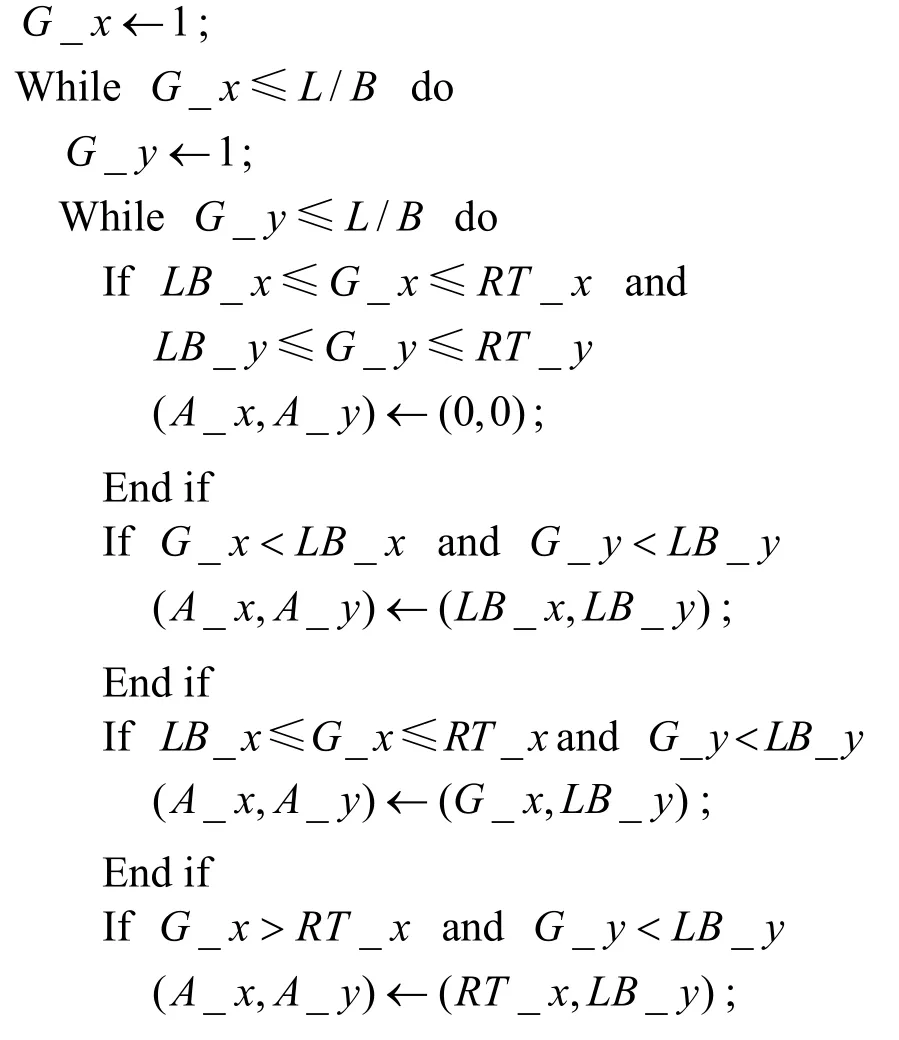
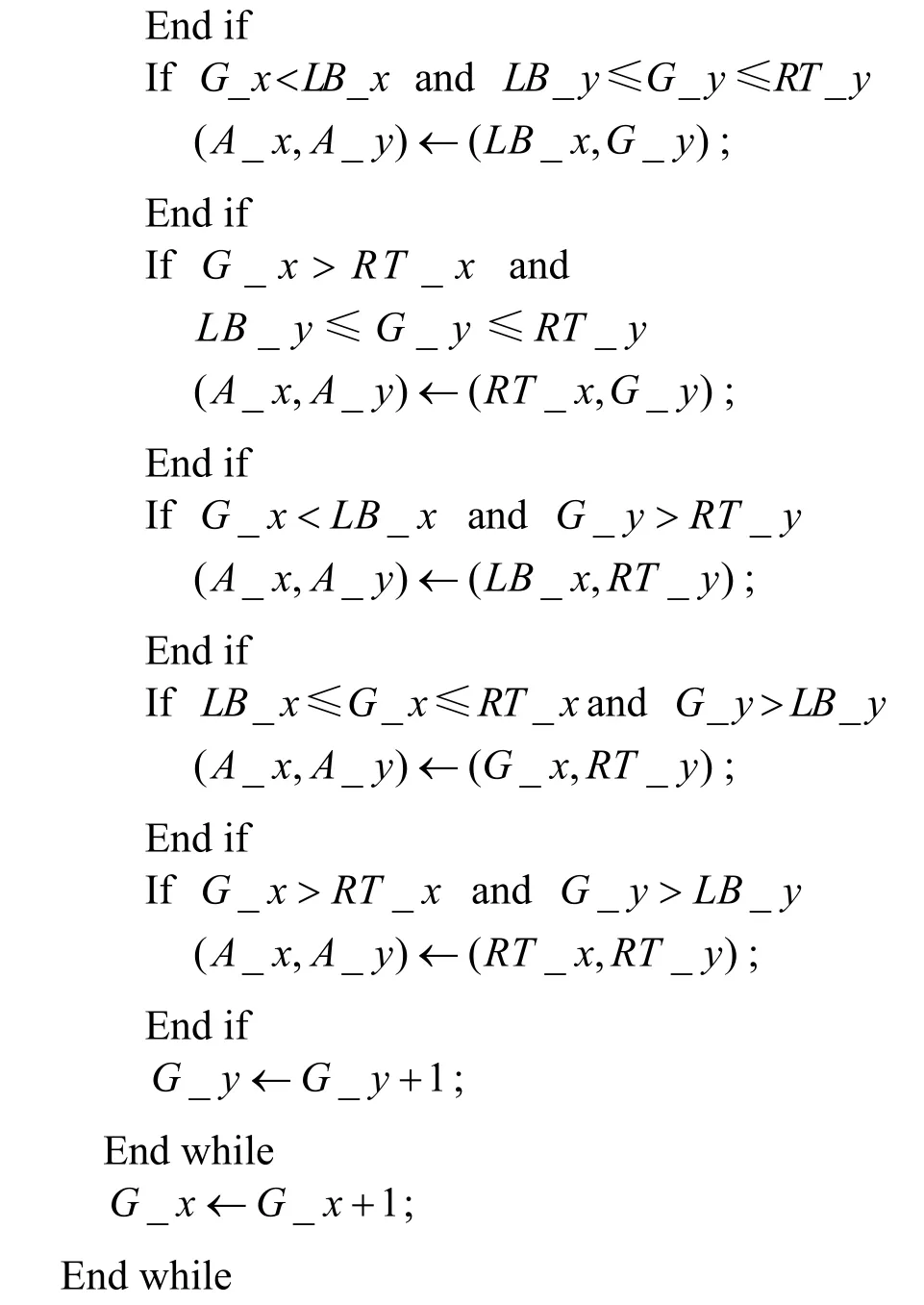
算法3 確定柵格下一跳的算法偽碼

在確定了每個柵格的下一跳目的地之后，整個網絡就形成了以柵格為單位的從柵格到基站的有向連通結構，每個柵格都能夠直接或間接與基站連通，如圖3所示。

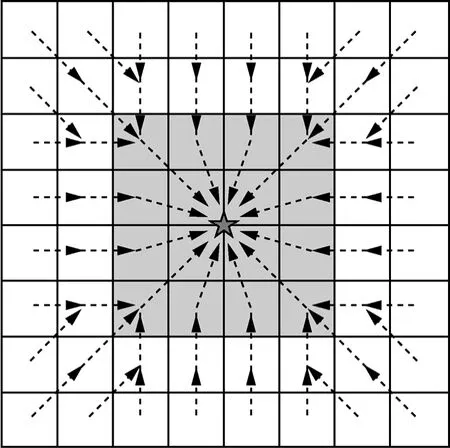
圖3 從柵格到基站的有向連通結構示意

為了能夠實現數據的融合并提高通信效率，還需要確定通信時隙，在同一條鏈路上，按照由遠及近的原則以柵格為單位發送數據，從而使中間柵格內的節點能夠進行數據的融合處理。另外，如果相互之間不會產生干擾，不同鏈路的多個柵格可以同時進行數據的傳輸。

基于所收集的節點信息和柵格劃分的結果，基站能夠獲得每個柵格中所分布的節點信息，從而可以為每個柵格以及柵格內的節點分配時隙。當然，分配時隙的時候必須要考慮網絡的動態變化。

同一個柵格內節點的時隙先后順序可以按照一定規則確定，如按照節點標識從小到大排列，設柵格(G_x,G_y)內的i個節點標識排列為N_1，N_2，…，N_i，設基站為該柵格分配的時隙表示為(G_x，G_y，T0，TN，T1，i，N_1，N_2，…，N_i)，其中，T0為該柵格時隙開始的時刻，TN為單個節點發送數據所需時間的期望值，T1為預留時隙長度。設置預留時隙是為了提高算法的動態適應能力，因為可能出現節點移動等情況使得某些柵格內分布的節點發生變化。柵格時隙的時間長度、節點N_k(1≤k≤i)時隙的開始時刻Tk和預留時隙開始時刻Tr分別為

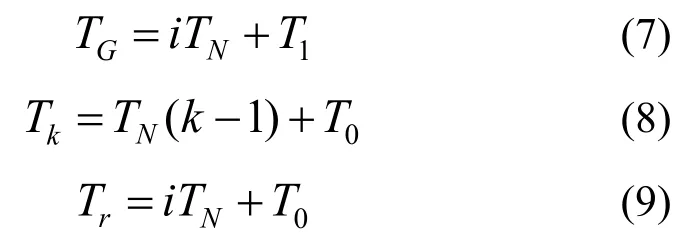
預留時隙可以根據應用需求由基站動態確定，不同輪的預留時隙可以不同，同一輪中的各個柵格的預留時隙也可以不同。

上述工作完成之后，基站就向網絡中的所有節點廣播當前輪數、部署區域起始點坐標、基站位置坐標、柵格邊長、每個柵格的下一跳目的地、每個柵格以及柵格中節點的時隙等信息以發起一輪數據收集，節點接收廣播消息并將這些信息保存在本地。

4.2 穩定階段

在穩定階段，每個節點首先根據本輪基站廣播的相關信息以及自己的位置確定節點所屬柵格、下一跳目的地、數據傳輸的距離、需要接收的上一跳柵格標識以及發送數據時隙等信息，在收發數據時，節點接收上一跳柵格內的所有節點發送的數據并和自己感知的數據進行融合處理，最后在相應的時隙中向下一跳目的地發送數據。和其他同類算法一樣，SFDA算法并不對采用何種融合處理方式進行限定，而是在應用中根據具體的需求，采用合適的融合處理方式。

首先，每個節點如節點j根據自己當前的位置坐標(j_x,j_y)確定自己所處柵格的標識，然后從保存的基站廣播信息中查找該柵格對應的下一跳目的地和所有以其為下一跳目的地的柵格。如果下一跳目的地的標識為(0,0)，則說明該節點需要直接向基站發送數據，它的最小數據傳輸距離D_min為節點與基站之間的距離，否則，它的下一跳目的地就是某個柵格，設該柵格的標識為(G_x,G_y)，則該節點的最小數據傳輸距離為它與這個柵格的4個頂點距離中的最大值。在理想條件下，最小數據傳輸距離就能夠滿足數據傳輸的需求，但在實際應用中，數據的實際傳輸距離會小于節點發送數據時所使用的數據傳輸距離，因而，需要在最小數據傳輸距離之上再增加一定的預留距離Dr，以確保數據傳輸的可靠性。同樣的，預留距離的大小也取決于具體的應用，每個節點的預留距離也可由節點分別確定。節點j確定數據傳輸距離D的算法描述如下：

算法4 節點確定數據傳輸距離的算法偽碼

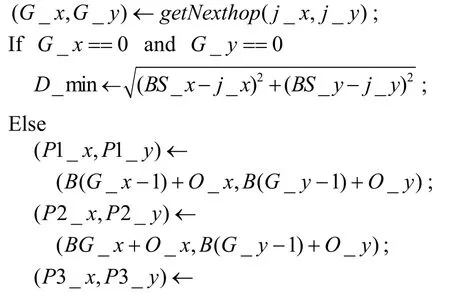
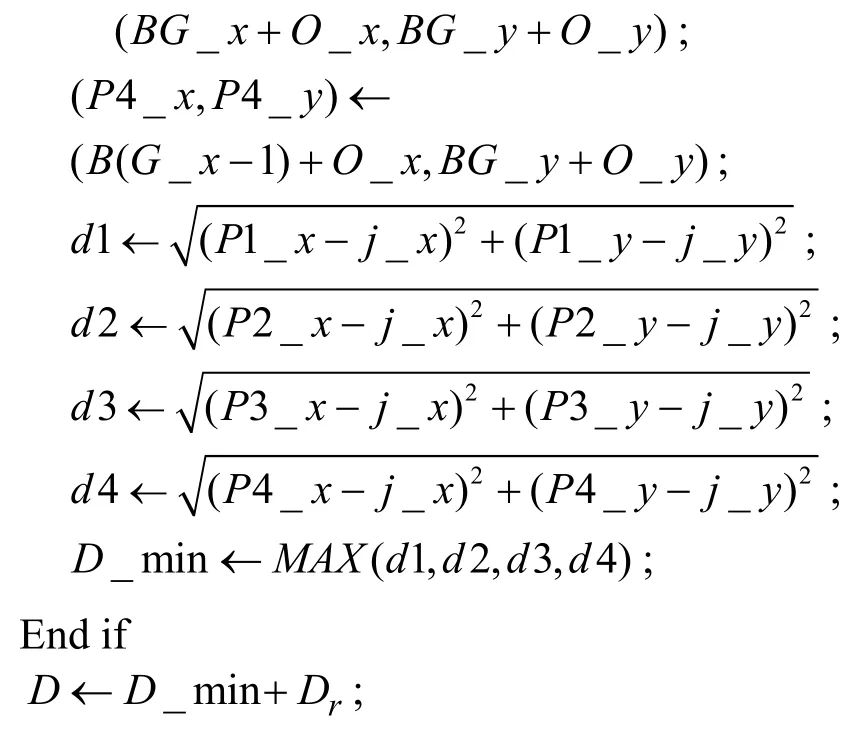
節點接收到其他節點發送的數據消息時，首先檢查該消息是否來自其上一跳柵格，如果不是，不接收該消息，否則，接收該消息。節點在自己發送數據之前將所有接收的數據與自己感知的數據進行融合處理，融合處理的方式可以根據應用需求選擇。

發送數據時，各個節點根據時隙信息在相應的時隙內發送數據。首先，節點從所屬柵格的時隙信息中查找自己的節點標識，如果節點標識在時隙信息中，則節點計算自己時隙的開始時刻，并在該時刻到來時檢測信道是否可用，如果信道可用，則發送數據，如果信道不可用，節點先隨機生成一個延遲，待該延遲結束時再檢測信道是否可用，然后決定是否發送數據，如果還不能發生數據，則重復上述操作，直至完成數據發送或者節點的時隙結束；如果節點標識不在所屬柵格的時隙信息中，該節點就在柵格的預留時隙內發送數據，在柵格的預留時隙開始時，節點首先隨機生成一個延遲，待該延遲結束時再檢測信道是否可用，如果信道可用，則開始發送數據，否則，就重復上述隨機等待，檢測信道，決定是否發送數據的操作，直至完成數據發送或者柵格時隙結束。算法5描述了節點在相應時隙中發送數據Data的操作。

算法5 節點發送數據操作的算法偽碼

節點在發送數據時，附帶將節點標識、所屬柵格標識等信息一起發送。另外，為了提高動態適應性，所有在本輪中未發送數據的節點都定期檢測自己的位置并確定所屬柵格信息，如果節點的所屬柵格改變，則節點立即更新相關信息，并準備在相應時隙發送數據，從而盡量確保其仍然能夠發送數據。

5 SFDA算法分析

本節主要從網絡動態適應性和能量消耗2個方面對SFDA算法進行分析。

在基于結構的算法中，必須預先在節點之間建立某種結構，然后再按照結構傳輸數據，這種結構可以看作是節點之間的一個有向連通圖，每個節點與其下一跳節點連接，也就是說，每個節點在發送數據之前都必須清楚自己需要將數據發送至哪個節點、數據傳輸距離是多遠。而在SFDA算法中，設置階段將網絡劃分為多個正方形柵格后，節點的數據傳輸就可以按照柵格為單位分類進行，每個節點（直接向基站發送數據的節點除外）只需知道將數據發送至哪個柵格，而不需要知道接收數據的是哪個或哪些節點，也就是說，節點在發送數據之前，只需要知道數據的傳輸距離，而不需要知道目的地節點，也就沒有基于結構算法所建立的那種由每一個節點與另外一個節點連接而構建的確定結構。如果網絡中的節點動態變化，在基于結構的算法中，只要結構還沒有更新，節點之間的連接就不會改變，也就對動態變化做出反應。而在SFDA算法中，節點則可以通過定期檢測來更新自己的下一跳柵格。

WSN的新應用中，網絡動態變化的原因主要分為節點從網絡中退出、節點在網絡中移動以及新的節點加入網絡3種。

節點從網絡中退出的情況有2種，一種是節點移動到了網絡部署區域之外，另一種則是節點雖然還在網絡中但由于節點故障、能量耗盡等因素造成節點無法正常工作。在采用“多對一”或“一對一”數據通信方式的數據融合算法中，如果某些節點退出網絡，則可能會造成以這些節點為轉發節點的所有節點都無法將數據發送至基站。而SFDA以柵格為單位進行數據通信，是一種“多對多”的數據通信方式，這樣，即使某些節點退出網絡，只要柵格中還分布有節點，則仍然可以實現數據的有效收集。

對于節點在網絡中移動的情況，SFDA使節點定期檢測位置信息，如果節點沒有離開原來的柵格，則不會產生任何影響，否則，節點能夠及時更新相關信息從而仍然可以發送數據，所以，節點在網絡中的移動對數據的收集影響很小。而在基于結構的算法中，如果節點的移動破壞了所建立的結構，相關節點的數據都無法發送至基站，從而會影響網絡的數據收集。

因為節點加入網絡而引起的網絡動態變化對SFDA的影響與其他算法類似，只有在新一輪開始之前加入網絡的節點才能夠發送數據。

在能量消耗方面，“多對多”的數據通信會增加節點的數據接收量，額外消耗一定的能量，實際上就是以能量為代價換取數據通信的可靠性。雖然如此，SFDA以柵格為單位對進行數據的“多對多”傳輸，某個柵格的節點只將數據發送至一個鄰近柵格內的節點，限制了重復接收數據節點的個數，另外，節點發送數據的距離只能覆蓋其鄰近柵格，限制了節點發送數據的距離，從而盡量降低了額外的能量開銷。再者，算法只增加了數據接收次數而并沒有增加數據發送次數，考慮到接收數據的能耗大大小于發送數據的能耗，所以，SFDA的額外能耗并不高。

由于SFDA所針對的是WSN的新應用，這些網絡部署在日常環境中，通過人工或其他方式為節點更換電源或為電源充電具有一定的可行性。所以，在這些應用中，節能位于次要位置，數據通信的可靠性才是首要考慮，因而，SFDA對網絡動態變化的適應能力強、可實現高可靠的數據通信，能夠以較小的能耗代價滿足這種應用需求。

需要說明的是，SFDA算法采用了不同于現有數據融合算法的數據傳輸方式，因為任何2種數據融合算法可以被同一個無線傳感器網絡分別采用但卻不能在一次數據收集中同時使用，所以，對于同一個無線傳感器網絡，可以采用SFDA算法的數據傳輸方式，也可以采用包括基于結構算法在內的其他數據傳輸方式，但是，不能在同一次數據收集中同時采用2種方式。此外，SFDA算法的“無結構”是指不需要為數據傳輸而在節點之間建立每一個節點與另外一個節點連接的結構，并非指組網結構，所以，在有結構的無線傳感器網絡中，SFDA算法并不會影響網絡自身的數據傳輸，網絡的結構對SFDA算法也沒有影響。

6 仿真實驗及結果分析

本文在 MATLAB平臺上進行對比仿真實驗，考察SFDA算法對網絡動態變化的適應能力以及能量消耗情況，并與其他幾種算法進行比較。因為現有的無結構數據融合算法都是針對事件觸發式，而在基于平面結構算法中，定向擴散算法是基于查詢式、SPIN算法是基于事件觸發式，與本文 SFDA算法所針對的周期性匯報式數據收集有所不同，所以，從基于分簇結構、樹狀結構和鏈路結構算法中分別選擇一種具有代表性的、可應用于周期性匯報式數據收集的算法與本文的算法進行對比實驗，它們分別是LEACH算法、GIT算法和PEGASIS算法。

6.1 仿真實驗環境

網絡部署區域邊長、基站位置、節點總數、SFDA的柵格邊長都作為可設置參數，LEACH的每輪簇首期望數目依據文獻[7]確定為節點總數的 5%，以使LEACH達到較好的性能。融合處理能夠將若干個長度相同的數據消息分組融合為一個仍為該長度的數據消息分組，其他仿真實驗參數的設置如表1所示。

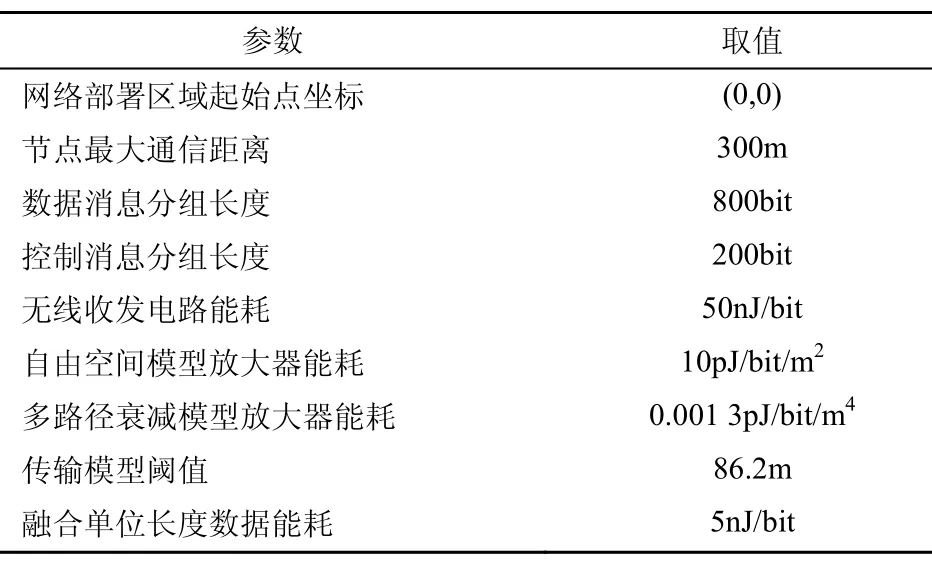
表1 其他仿真實驗參數的設置

6.2 仿真實驗結果分析

首先比較各個算法對網絡動態變化的適應能力。由于節點新加入網絡對幾種算法的影響相同，因此，仿真實驗只考察算法對節點在網絡中移動或退出網絡所造成的網絡動態變化的適應能力。如果節點因為在網絡中移動或退出網絡而導致節點無法正常收發數據，則稱該節點失效。因為幾種對比算法都是針對節點位置固定而非節點移動的應用場景而設計的，所以實驗不考慮導致節點失效的具體原因，而只設置節點的失效概率，每次對比實驗中，各個算法的初始狀態、失效的節點（失效節點總數以及哪些節點失效）都是相同的，從而使實驗結果具有可比較性。分別進行多次對比仿真實驗，每次對比仿真實驗中幾種算法的節點失效概率相同，統計仿真實驗中產生的連帶失效節點的數目，所謂連帶失效節點是指節點自身沒有失效但是因為其他節點失效而無法將數據發送至基站的節點。相同條件下，算法的連帶實效節點的數目越小，就說明算法越能夠適應網絡的動態變化。

每次對比仿真中節點的失效概率均相同，網絡部署區域邊長為200m，基站位置為(100, 100)，網絡中均勻分布有1 200個節點，SFDA的柵格邊長為20m，每個算法的仿真分別進行100輪，節點失效概率為0.01～0.09和0.1～0.9的仿真結果分別如圖4和圖5所示。可以看出，在相同的條件下，SFDA、LEACH、GIT和PEGASIS的連帶失效節點平均數依次遞減，而且，SFDA的連帶失效節點平均數都要遠遠小于其他幾種算法。在節點失效概率小于0.4時，SFDA幾乎沒有連帶失效節點產生，隨著節點失效概率的增大，SFDA的連帶失效節點也只是緩慢增加，而其他幾種算法的連帶失效節點則較多，尤其是GIT和PEGASIS，在節點失效概率較大時，幾乎沒有節點能夠成功將數據傳輸至基站，主要原因是這些算法的關鍵節點較多，而一個關鍵節點的失效就可能影響其他很多節點的數據傳輸。仿真結果證明，使用SFDA算法，網絡動態變化對網絡數據收集的影響比使用LEACH、GIT和PEGASIS要小得多，SFDA對網絡動態變化的適應能力更強、能夠提供更為可靠的數據通信。

對于SFDA算法，在同一應用場景中，柵格邊長取值的不同以及基站所處位置的不同都會給SFDA算法對網絡動態變化的適應能力造成影響。保持上述實驗場景的其他條件不變，分別設置不同的柵格邊長和改變基站的位置，每次仿真100輪，考察連帶失效節點平均數，分析柵格邊長和基站位置對SFDA算法的動態變化適應性的影響。

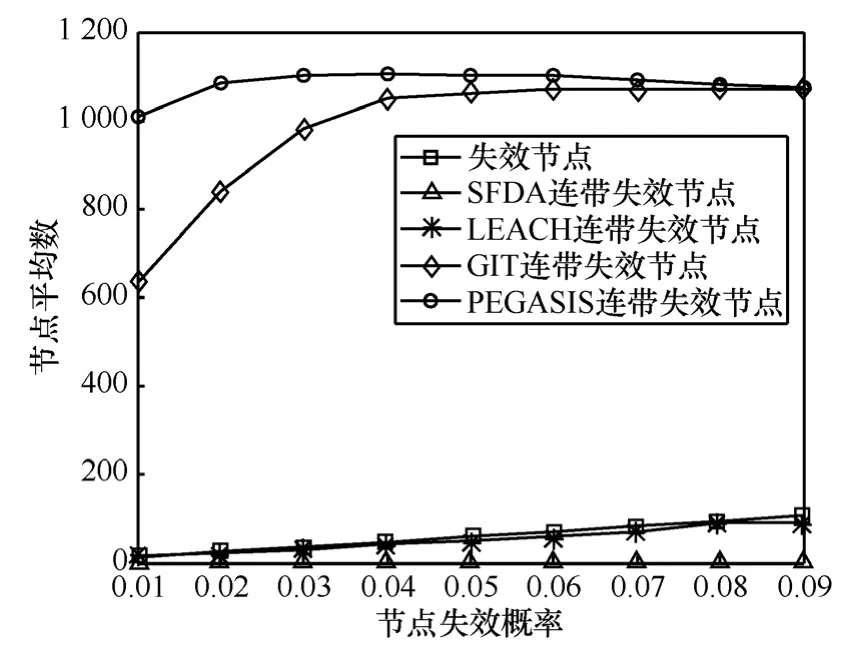
圖4 節點失效概率為0.01～0.09的仿真結果

圖5 節點失效概率為0.1～0.9的仿真結果

柵格邊長分別為20m、25m和40m時，在不同節點失效概率的情況下，實驗中網絡產生的連帶失效節點平均數如圖6所示。柵格邊長的取值越大，產生的連帶失效節點越少，這就說明，柵格邊長越大，SFDA算法對網絡動態變化的適應能力越強。在SFDA算法中，連帶失效節點的產生原因是處于中間的柵格內的所有節點都失效，從而造成以中間柵格內的節點為中繼節點的其他相關柵格內的有效節點無法完成數據傳輸而失效。柵格邊長取值越大，柵格就越大，在節點均勻分布的情況下，柵格內的節點也就越多，在節點失效概率相同時，柵格內所有節點都失效的可能性就越小，此外，柵格邊長越大，網絡中的柵格就越少，相同節點將數據發送至基站所需的跳數就越少，數據傳輸失敗的可能性也越小。因而，柵格邊長越大所產生的連帶失效節點就越少，對網絡動態變化的適應能力就越強。當然，柵格邊長也不是越大就越好，在上述實驗條件下，如果柵格邊長達到50m，則所有的柵格都是臨近柵格，也就是說，所有的節點都直接將數據發送至基站，而且柵格越大，節點發送數據的距離就越大，能耗也越多，如何確定最優的柵格邊長以平衡各方面的性能將是未來研究的重點。

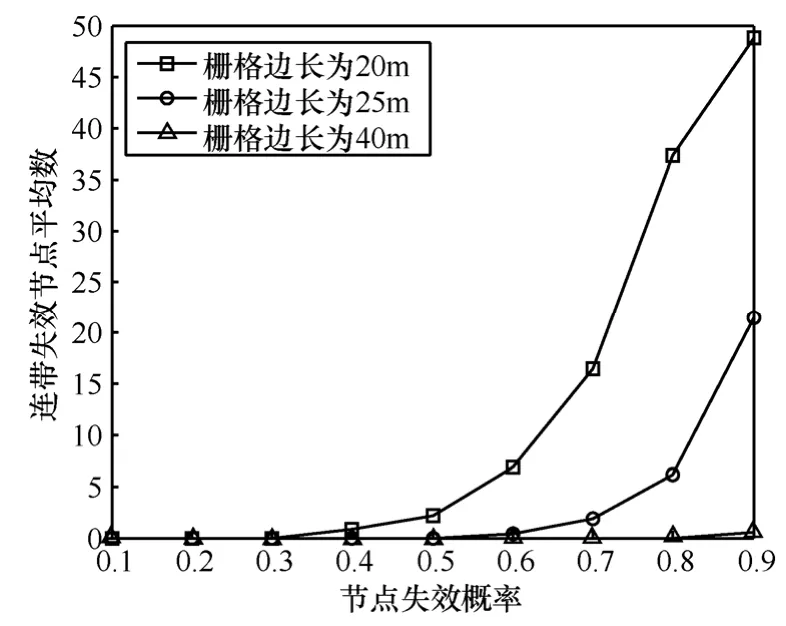
圖6 柵格邊長對SFDA算法的動態變化適應性的影響

將基站位置分別設置為(100，100)、(100，110)和(110，110)，使基站分別位于柵格頂點、柵格邊界和柵格內部，在不同節點失效概率的情況下，網絡產生的連帶失效節點平均數如圖7所示。上述3種情況產生的連帶失效節點依次遞增，說明對網絡動態變化的適應能力依次減弱。主要是因為網絡中臨近柵格數目不同而造成的，基站位于柵格頂點時臨近柵格最多，位于柵格邊界時次之，位于柵格內部時最少。臨近柵格越多，則直接向基站發送數據的節點越多，可能出現連帶失效的節點就越少。另外，臨近柵格越多，為其他柵格內節點向基站傳輸數據提供中繼服務的柵格就越多，以每個這樣的柵格為中繼的節點數目就越少，如果某個這樣的柵格內的所有節點都失效，其所造成的連帶失效節點也就越少。因此，應設置基站的位置使得臨近柵格的個數盡量多，以提高網絡的動態適應能力。

圖7 基站位置對SFDA算法的動態變化適應性的影響

再對比幾種算法的能耗。分別為SFDA設置不同的柵格邊長、基站位置、節點數目、網絡部署區域邊長，既比較幾種算法的能耗，也對相關參數對SFDA能耗的影響進行考察。每次條件相同的仿真分別進行100輪，統計節點發送消息、接收消息和融合數據的能耗。最后，比較不同條件下幾種算法平均每輪整個網絡和每個節點的能耗，仿真結果如表2所示。從表中的實驗結果可以看出，SFDA的能耗在大多數情況下都高于GIT和PEGASIS，只有在柵格邊長較小時，SFDA的能耗才低于GIT和PEGASIS，但是，與LEACH相比，SFDA的能耗性能在大多數情況下都更好，只有在柵格邊長較大時，SFDA的能耗才高于LEACH。主要是因為在GIT和PEGASIS算法中，節點只需要向距離較近或距離最近的節點發送數據，所以它們的能耗性能較好。雖然SFDA算法的能耗性能在某些條件下不及一些能耗性能較好的基于結構算法，卻仍然要優于其他一些基于結構算法。

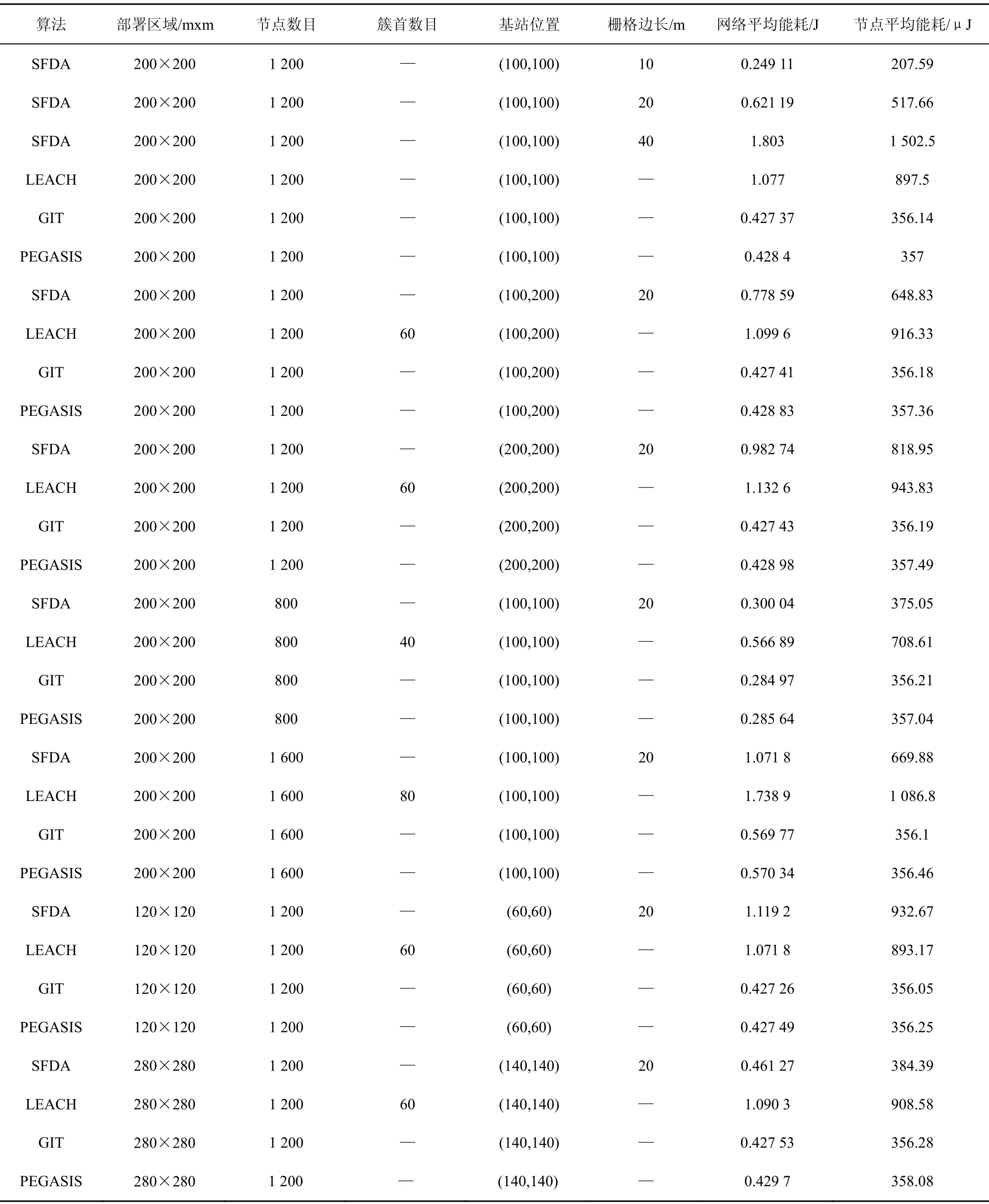
表2 能量消耗仿真結果

另外，分析能耗仿真結果可以得出，在其他條件相同時，柵格邊長越小能耗越小，因為柵格越小，每個柵格內的節點越少、節點傳輸數據的距離越短，所以接收和發送數據的能耗就越小；基站的位置越靠近網絡的中心能耗越小，因為基站越靠近網絡中心，負責轉發數據的柵格就越少，從而降低了能量消耗；節點總數越少能耗越小，因為節點總數越少則分布在每個柵格中的節點也會越少，轉發柵格內的節點接收的數據量就越小，從而減小了能耗；網絡部署范圍越大能耗越小，因為部署范圍越大，每個柵格內的節點就越少，節點數據接收量減少，但是柵格大小沒有變化，發送距離也沒有變化，所以能耗也會減小。

7 結束語

本文分析了WSN在的一些新應用中出現的新特點——網絡動態變化更加頻繁、對數據通信的可靠性要求更高，針對現有數據融合算法在這些應用中的不足，提出了適用于周期性匯報式數據收集的SFDA算法，它是一種無需在節點之間建立和維護結構、采用“多對多”數據通信方式的無線傳感器網絡數據融合算法，對網絡動態變化具有很強的適應能力，并能夠提供高可靠性的數據通信。仿真實驗結果表明，SFDA在網絡動態適應性方面具有較大的優勢，額外的能耗代價也較小，能夠滿足新應用需求。

本文對無結構數據融合這類新穎的數據融合算法進行了探索式的研究，還有許多內容需要進一步探討，也有較多問題亟待解決。下一步工作主要包括以下幾個方面：1)針對不同形狀的網絡部署區域、不同的柵格形狀等情況進行研究，以增強算法的適用性；2)通過定量的方法確定相關參數如柵格邊長的最佳取值，以優化算法的性能；3)針對另外一些應用中可能出現的節點分布不均勻、節點失效概率不同或節點異構等情況，擴展算法以提高算法的健壯性和擴大算法的應用范圍；4)研究提出節點數據傳輸的詳細調度方法。

[1] AKYILDIZ I F, SU W, SANKARASUBRAMANIAM Y. A survey on sensor networks[J]. IEEE Communications Magazine, 2002, 40(8):102-114.

[2] 馬祖長, 孫怡寧, 梅濤.無線傳感器網絡綜述[J].通信學報, 2004,25(4): 114-124.MA Z C, SUN Y N, MEI T. Survey on wireless sensor network[J].Journal on Communications, 2004, 25(4): 114-124.

[3] KRISHANAMACHARI B, ESTRIN D, WICKER S. The impact of data aggregation in wireless sensor networks[A]. Proceedings of International Workshop of Distributed Event Based Systems[C]. Vienna,Austria, 2002. 575-578.

[4] RAJAGOPALAN R, VARSHNEY P K. Data-aggregation techniques in sensor networks: a survey[J]. IEEE Communications Surveys &Tutorials, 2006, 8(4): 48-63.

[5] INTANAGONWIWAT C, GOVINDAN R, ESTRIN D. Directed diffusion for wireless sensor networks[J]. IEEE/ACM Transcations on Networking, 2003, 11(1): 2-16.

[6] KULIK J, HEINZELMAN W R, BALAKRISHNAN H. Negotiation-based protocols for disseminating information in wireless sensor networks[J]. Wireless Networks, 2002, 8(1): 169-185.

[7] HEINZELMAN W R, CHANDRAKASAN A, BALAKRISHNAN H.Energy-efficient communication protocol for wireless microsensor networks[A]. Proceedings of International Conference on System Sciences[C]. San Francisco: IEEE Computer Society, USA, 2000.3005-3014.

[8] YOUNIS O, FAHMY S. HEED: a hybrid, energy- efficient, distributed clustering approach for ad hoc sensor networks[J]. IEEE Transcations on Mobile Computing, 2004, 3(4): 366-379.

[9] KRISHNAMACHARI B, ESTRIN D, WICKER S. Modeling data centric routing in wireless sensor networks[A]. Proceedings of IEEE International Conference on Information Communications[C]. New York: IEEE Computer Society, USA, 2000. 1-18.

[10] LINDSEY S, RAGHAVENDRA C. PEGASIS: power-efficient gathering in sensor information systems[A]. Proceedings of IEEE Aero-space Conference[C]. Montana: IEEE Aerospace and Electronic Systems Society, USA, 2002. 1125-1130.

[11] TABASSUM N, URANO Y, HAQUE A. GSEN: an efficient energy consumption routing scheme for wireless sensor network[A]. Proceedings of IEEE International Conference on Networking[C]. Washington: IEEE Computer Society, USA, 2006. 117-122.

[12] OKEKE B C, LAW K L E. Multi-level clustering architecture and protocol designs for wireless sensor networks[A]. Proceedings of International Conference on Wireless Internet[C]. Hawaii, USA,2008. 1-9.

[13] CHAO C M, HSIAO T Y. Structure-free data aggregation in sensor networks[J]. IEEE Transactions on Mobile Computing, 2007, 6(8):929-942.

[14] FAN K W, LIU S, SINHA P. Design of structure-free and energy-balanced data aggregation in wireless sensor networks[A]. Proceedings of IEEE International Conference on High Performance Computing and Communications[C]. Washington: IEEE Computer Society, USA, 2009. 222-229.