基于極限平衡法的邊坡穩定性分析

邱 阜 彭振斌

（1.中南大學地球科學與信息物理學院 湖南 長沙 410012；2.長沙市天心區建設局 湖南 長沙 410000）

0 引言

邊坡穩定性分析方法主要分為極限平衡法與數值分析方法，極限平衡方法分析邊坡穩定性具有簡單、快捷的特點。而數值分析方法主要利用數值計算軟件對邊坡開挖、支護過程進行模擬，計算精度較高，但由于建模分析相對繁瑣，在工程中并未得到廣泛的推廣應用。 隨著計算機水平的發展，極限平衡方法逐漸被軟件化，出現了以geo-studio、slide 等為代表的一批基于極限平衡方法的邊坡計算軟件，為相關工程的設計計算提供了方便，并得到了廣泛的應用。 如萬文[1]運用極限平衡法對某高速公路邊坡穩定性及支護措施進行了模擬，探討了Janbu 法、Bishop 法、Morgenstren-Price 計算方法在邊坡穩定性計算中的不同點。 得到了一些有益的結論。 而曾鈴[2]運用極限平衡方法對某邊坡滑移面的抗剪強度參數進行了反演分析，得到了與實際相符的計算參數。 由此可見，利用極限平衡方法分析邊坡穩定性已經得到了廣泛應用。 因此，本文在總結前人研究成果的基礎上， 基于極限平衡計算軟件，對某邊坡初始穩定性及處治措施進行了研究，為設計與施工提供了參考依據，具有一定的現實意義。

1 極限平衡計算原理及方法

1.1 極限平衡計算原理

分析巖體和土體穩定性時假定一破壞面, 取破壞面內土體, 為脫離體計算出作用于脫離體上的力系達到靜力平衡時所需的巖土的抗力或抗剪強度, 與破壞面實際所能提供的巖土的抗力或抗剪強度相比較,以求得穩定性安全系數。安全系數根據定義可表示為[3]：

式中：Fs為安全系數，τf為滑動面上的抗滑力，τ 為滑動面上的實際滑力。

極限平衡分析方法最早是1961 年由瑞典人彼得森提出來的，他將邊坡潛在滑移面以上的土體劃分成若干個垂直條塊，在計算過程中進行了一定的假設，假設條塊間沒有相互作用力的存在，定義安全系數為潛在滑移面上的抗滑力矩與滑動力矩之比為邊坡安全系數。 隨著科學技術的研究的不斷深入，廣大學者在此基礎上對其進行了優化[4-5]，出現了以Bishop 法、Janbu 法、Morgenstren-Price 等一系列簡化方法。 限于篇幅本文只對Bishop 法進行詳細介紹。

1.2 Bishop 簡化計算方法

簡化的Bishop 法假設滑移面的形狀為圓弧形[6-7]，土條之間只有水平推力，條間剪力為零，計算見圖如圖2 所示。

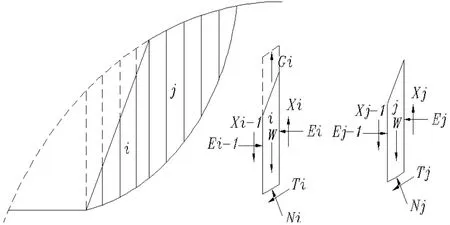
圖1 BISHOP 計算簡圖

作用在第i 條塊上的力有重力（W）、開挖面的法向力（Nci）和切向力（Tci）、條塊分界面上的法向力（Ei，Ei-1）和切向力（Xi，Xi-1）以及潛在滑動面上法向力（Ni）和切向力（Ti）。 li為第i 條塊底邊長度，αi為第i 條塊底邊與水平面的夾角，ci為第i 條塊的巖土體內聚力，φi為第i 條塊巖土體的內摩擦角。

土條間滿足:

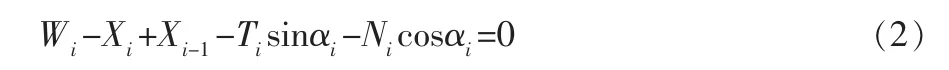
假定土坡安全系數為K， 則土條i 滑動面上的切向力滿足以下關系：

聯立式（2）和式（3）得

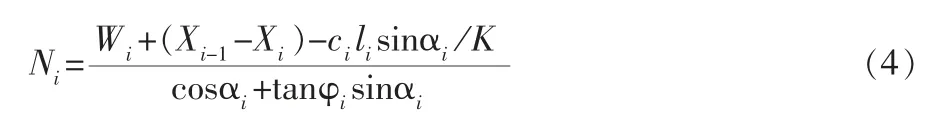
根據邊坡安全系數定義

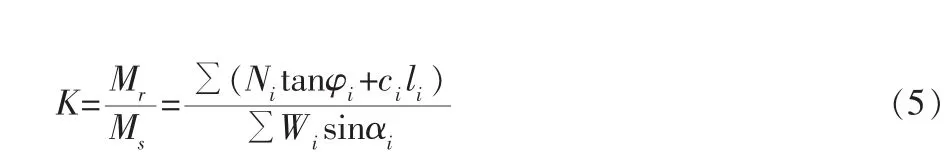
整理得:

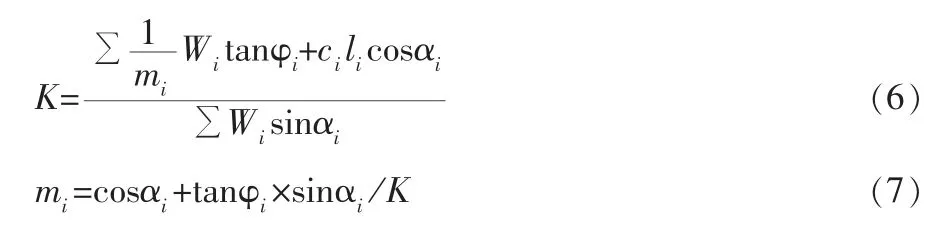
2 工程概況

長沙市天心區新天村安置小區南側邊坡位于長沙市天心區新開鋪街道辦事處新天村內。 該邊坡高約7-14m 邊坡，邊坡分為三級，從上往下分別高4 米、7 米、3 米，坡頂有一平房。邊坡做了簡易掛網噴漿處理，2011 年1 月8 日，邊坡體由于降雨發生了潛在的滑坡， 在其牽引力作用下產生了張裂縫，其穩定性受到了破壞，在有關專家指導下進行了坡腳反壓與坡頂卸載相結合的搶險處理， 坡體基本處于穩定狀態。因此需對其進行支護處理， 以保證其邊坡的長期穩定性，邊坡典型剖面見圖2 所示。

根據鉆孔柱狀圖可知，各巖土層成層條件為：

（1）粉質粘土：灰白、褐黃色，沉積層理清晰可辨，含薄層粘土，稍濕，硬塑～堅硬狀態。

（2）中砂：褐黃色，石英質成分，不均勻含圓礫5-10%，混5-10%粘性土，稍濕，中密狀態。

（3）粗砂：褐紅色，石英質成分，不均勻含圓礫5-15%，混7-15%粘性土，中濕，中密狀態。

根據勘察報告，地下水類型為上層滯水及潛水，上層滯水水量有限，潛水水量較大。 水質分析表明，場地地下水對混凝土結構、混凝土中的鋼筋無腐蝕性，對鋼結構具弱腐蝕性。

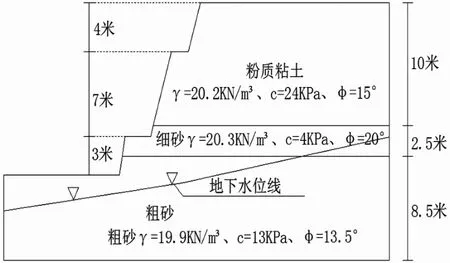
圖2 邊坡典型剖面

3 邊坡穩定性分析

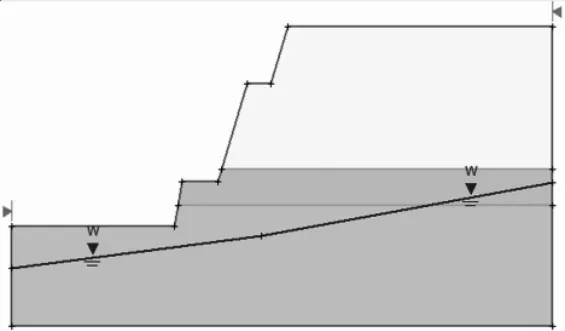
圖3 邊坡典型剖面數值計算模型

3.1 邊坡計算模型的建立與計算參數

為了分析該邊坡的穩定性， 并提出合理的治理方案，本文選取邊坡最危險剖面作為穩定性分析的對象，以保證其邊坡穩定性能夠得到最大的保障，與圖2 想對應的邊坡典型剖面數值分析模型如圖3 所示。

為了準確、可靠地對邊坡穩定性進行分析，以起到為邊坡的治理提供科學的的依據的目的，本文選用勘察資料所述各鉆孔土樣抗剪強度平均值為最終計算值，各層巖土體物理力學參數見表1。

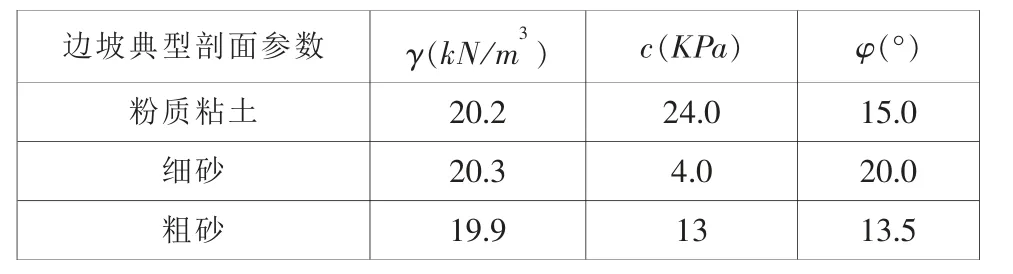
表1 邊坡物理力學參數

3.2 無支護條件下邊坡穩定性分析

圖4 為邊坡在自然無支護條件下的潛在滑移面相對位置圖，有圖可知，邊坡安全系數為0.998，其安全系數的大小不能滿足規范所要求的最小值。 由此可見：邊坡在無支護條件下的穩定狀態與實際觀測所得到了穩定性結論一致。 在無支護條件下能夠基本穩定， 但不能滿足規范所規定的最小值。 因此，需對邊坡進行治理，以保證其長期穩定性。

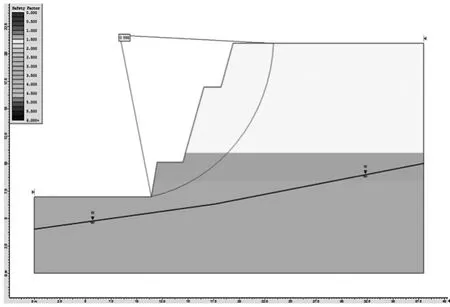
圖4 無支護條件下邊坡滑移面位置（Fs=0.988）

3.3 有支護條件下邊坡穩定性分析

鑒于邊坡在自然無支護條件下不能滿足其穩定性的現狀，筆者擬采用設計資料所推薦的邊坡治理方式對邊坡進行處治。 根據設計院推薦支護方式，采用如圖5 所示支護形式對邊坡進行支護。 其中，錨索抗拉強度為150kN，錨定板強度為150kN，粘結強度為2000kN/m，剪切強度為80kN。

利用極限平衡方法，對邊坡在圖5 所示支護措施條件下的穩定性進行計算，計算結果如圖6 所示，有圖可知，邊坡在錨索支護后安全系數為3.014， 大于規范所要求的最低安全系數標準，表明邊坡處于安全狀態。 由潛在滑移面的相對位置可知， 邊坡在該支護措施下發生淺層滑移的可能性較低，具有較高的安全保障。 由此可見，設計院所推薦的支護措施是行之有效的，能保證邊坡的長期穩定性。

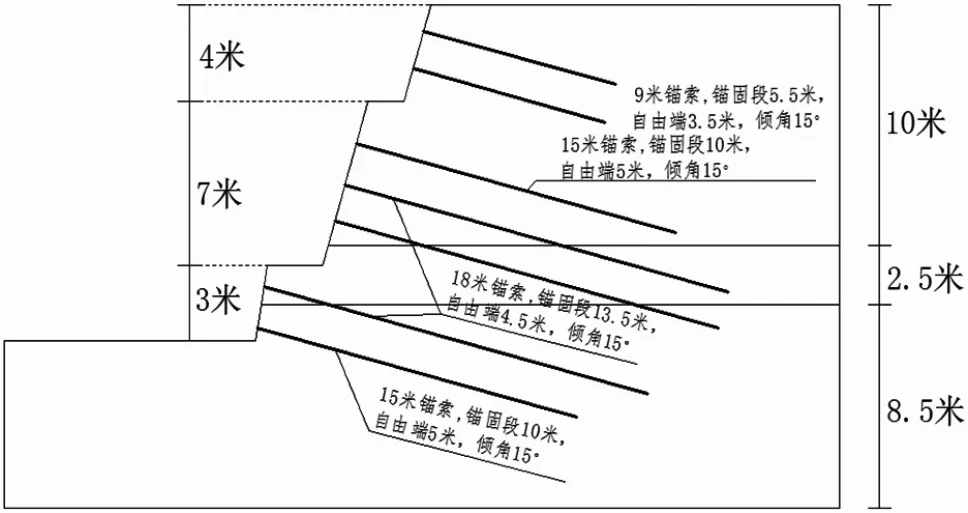
圖5 邊坡支護措施設計圖

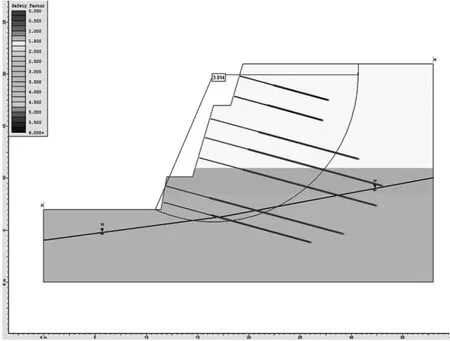
圖6 有支護措施條件下邊坡穩定性計算結果（Fs=3.014）

4 結論

本文基于實際巖土體物理力學參數， 利用極限平衡方法，對邊坡支護前后的穩定性進行計算分析，分析表明：

4.1 該邊坡在無支護條件下，安全系數為0.998，邊坡處于極限穩定狀態，與實際監測數據所呈現狀態想吻合，邊坡需進行及時治理。

4.2 依據設計院所推薦支護措施，對邊坡進行治理。經計算，邊坡在系統錨索支護作用下安全系數顯著提高，達到3.014。滿足規范歲要求的最低標準。 表明該支護措施對約束文中所述邊坡穩定性是行之有效的。

4.3 由計算結果可知， 利用極限平衡方法分析邊坡的穩定性具有計算準確、操作簡便等特點，具有廣泛推廣的現實意義。

［1］萬文，曹平，吳永恒.彈塑性極限平衡法分析復雜巖質邊坡的穩定性[J].中國安全科學學報，2004,14（6）:100-108.

［2］曾鈴，蔣中明，付宏淵.邊坡潛在滑移面抗剪強度參數反演研究[J].中外公路，2011,31（1）:23-25.

［3］李廣信.高等土力學[M].北京：清華大學出版社，2004.

［4］黃夢宏，丁樺.邊坡穩定性分析極限平衡法的簡化條件[J].巖石力學與工程學報，2006，25（12）:2529-2536.

［5］錢家歡，殷宗澤.土工原理與計算[M].2 版.北京：中國水利電力出版社，1996.

［6］Bishop A W，Alpan I,Bight G E，et a1.Factor controlling the shear，tren -gth of partly saturated cohesive soil [S].In ASCE Research Camferen on the Shear Strength of Cohesive Soils.Univ.of Colorado，1960，503-532.

［7］Bishop A W.Blight GE.Some aspects of effective stress in saturated and party satu-rated soil[J]. Geotechnique，1963,13（3）：177-197.